Bayro-Corrochano E., Scheuermann G. Geometric Algebra Computing: in Engineering and Computer Science

Подождите немного. Документ загружается.

258 Y. Xu et al.

mechanism of adaptive scale representation of geometric features is important to

alleviate the phase singularity problem.

It is known that objects in the world appear in different ways depending on the

scale of observation [16]. Here we use a set of quaternion Gabor ﬁlters as kernel

functions to give the complete scale representation of the original signal. During the

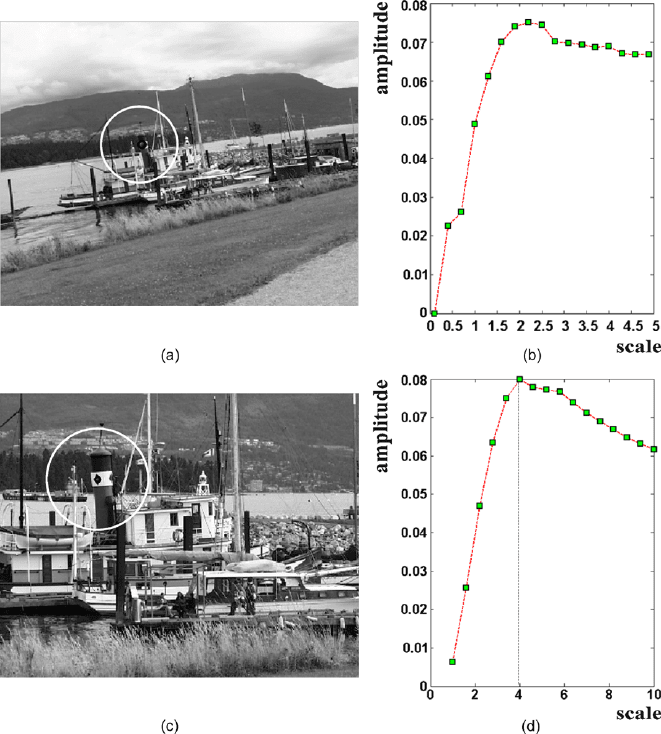
adaptation of the local scales of quaternion Gabor ﬁltering, as shown in Fig. 7,the

response at the given pattern reaches the maximum value at its characteristic scale

and descends at neighboring scales. When the scale of ﬁltering is rather far from

the characteristic scale of the local pattern, the amplitude is expected to be very

small, and thus the singularity problem arises. Therefore it is important to select

local appropriate scales for further analysis of unknown image pattern.

To robustly model the correspondence of point sets in an image pair, which are

captured at different time or views, our previous work proposed a phase-based data

measure for assignment a =(p, q) using adaptive-scale quaternion wavelet kernel

representation as below [4]:



a =(p, q)





σ ∈S





∈Ω



∈Ω





;σ







;σ











;σ



−φ





;σ



2π









;σ



−θ





;σ











;σ



−ψ





;σ



π/2





, (11)

where S is the scale-space of the given quaternion ﬁlter set, Ω

and Ω

are the

neighborhoods of the points p and q, respectively, ρ

and ρ

are the output ampli-

tude spectrums of two images, which either are the left and right views in the stereo

matching problem or the sample images captured at different time in the optical ﬂow

problem. The operator [Φ]

extracts the principal value of Φ within the range of

[−A/2,A/2). It is noted that the phase pattern (φ,θ,ψ)

in a local neighborhood

is directly used to set up the data measure and the absolute distance metric of two

phase patterns is weighted by the amplitude. As a result, only the phase values ex-

tracted by the quaternion wavelet kernels that well match the characteristic scale of

the given pattern with strong responses contribute to the data measure. Therefore the

mechanism of adaptive-scale kernel representation efﬁciently alleviates the negative

effects of phase singularity.

To further emphasize the importance of the mechanism of the adaptive scale

kernel representation, we give two comparison experiments to demonstrate the im-

provements introduced by this mechanism. As shown in Figs. 8 and 9, we compare

our computational model with Chan’s phase-difference model [3] for 2D shift esti-

mation between images, where the latter one is typical of the existing phase-based

method [1, 2].

Chan [3] used the phase-difference model to compute the disparity/optical ﬂow

ﬁeld. The phase singularities are detected and removed by threshold constraints of

magnitude and local frequency. Then the shift estimation would be given up if the

local structure cannot be captured under the given scale of the ﬁltering. In his pyra-

mid decomposition structure, these holes would outspread from coarse scales to ﬁne

QWT: Retrospective and New Applications 259

Fig. 7 Characteristic scales of two image patterns at the circle centers. (a), (c) Two images taken

with different zoom. (b), (d) The responses of the quaternion Gabors in scale space at two circle

centers

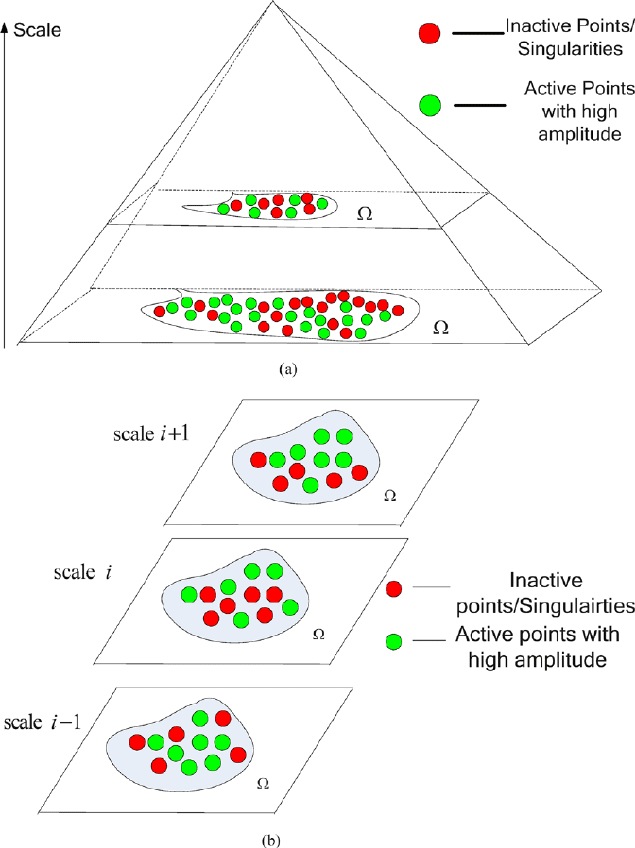
scales. In our model, we introduce the mechanism of the adaptive-scale kernel rep-

resentation and select two multiscale decomposition schemes to testify its validity.

For the disparity estimation, the pyramid decomposition structure is used to get the

multiscale phase structures. The phase singularities have chances to revival once

the disparity computation reaches their characteristic scales. In addition, the active

points with high amplitude serve an important role of propagating disparities within

their neighborhood Ω. Thus the singularities are still assigned a good match with

high probability as long as enough active points are distributed around. From coarse

scales to ﬁne scales, the inactive points/singularities and the active points might

exchange their roles according to the approximation of the current scale to their

260 Y. Xu et al.

Fig. 8 The transit of active points under the adaptive-scale kernel representation

characteristic scales (as shown in Fig. 8(a)). For the optical ﬂow computation, we

select a set of quaternion Gabors to successively cover the characteristic scales of

image structures. At each point, the phase structures are extracted by adaptive-scale

kernels, resulting in low density of phase singularities (as shown in Fig. 8(b)).

As shown in Fig. 9, the correct depth clues are obtained in our model, while it is

difﬁcult to distinguish objects of varied depth in Chan’s results under large disparity

QWT: Retrospective and New Applications 261

Fig. 9 Comparison of two computational models for disparity estimation

range. Less depth clues can be observed from vertical disparity map due to the

uniform distribution. According to the movement distribution in ground truth image

shown in Fig. 10, distinct improvement can also be observed in our optical ﬂow ﬁeld

as a comparison with Chan’s results in the “Yosemite” sequence. We only use two

Gabors in the optical ﬂow estimation to demonstrate the improvement introduced

by the adaptive-scale kernel representation. Better performance can be gained when

more successive-scale Gabors are used.

4 The Potential Use of QWT in Image Registration

It has been shown in Sect. 3 that quaternionic phases were a reliable tool to settle

the correspondence problem. Similar to most of existing matching methods, there is

262 Y. Xu et al.

Fig. 10 Comparison of two computational models for optical ﬂow estimation

an implicit assumption of weak foreshortening between the images. Thus the phase

structures can be compared at the similar scale in two views. However, this assump-

tion would be violated in wide baseline stereo, 3D model alignment, and creation

of panoramic views due to the two cameras far apart or with a large vergence angle.

The issue of image registration should be considered as one of these problems. Cur-

rently, the concept of afﬁne invariant features is proposed to deal with the distinct

afﬁne deformations under changing viewpoint [17]. In this section, we establish the

quaternionic phase congruency model to detect afﬁne-invariant features. Combin-

ing it with the scale invariant descriptor, it provides encouraging matching results in

image registration task.

The measurement of signiﬁcance is important for feature detectors. We always

expect only those highly distinguished features to be used in image registration.

Phase congruency model in complex wavelet domain has already been proved as a

dimensionless measure of feature signiﬁcance and demonstrates its superior behav-

QWT: Retrospective and New Applications 263

ior in noise and illumination invariance [18]. We extend this model to quaternion

wavelet domain and reveal the tighter constraint implied in the quaternionic phase

congruency model.

Here we ﬁrst analyze the phase congruency model in the quaternionic Fourier

domain; then the conclusions can be directly extended to the quaternion wavelet

domain since it can be considered as the windowed version of the former one. Trac-

ing back to (1), we give the deﬁnition of phase congruency function in quaternionic

Fourier domain as the extension of Morrone and Owens’s work [19]

(u, v) =



∞

−∞



∞

−∞

−iux

f(x,y)e

−jvy

dx dy. (1)

As for the real 2D signal f(x,y),(1) can be written as

(u, v) =



∞

−∞



∞

−∞

f(x,y)e

−iφ(x,y)

−jθ(x,y)

dx dy, (12)

where φ(x,y) =2πux and θ(x,y) =2πvy. We denote Φ as (φ, θ)

; then the def-

inition of quaternionic phase congruency function at point x = (x, y)

is based on

the function Φ:

PC(x) =



cos((Φ

(x) −

Φ(x)))



, (13)

where A

and Φ

respectively represent the amplitude and the phase vector of the

nth scale component in the quaternion space. The function

Φ(x) denotes the phase

vector of the composite vector formed from all the scale components. As follows, we

reveal the tighter constraint implied in the quaternionic phase congruency model as

compared with the one in CWT domain. An arbitrary 2D signal can be decomposed

into its symmetrical components as

(x, y) =



f(x,y) +f(−x,y) +f(x,−y)+f(−x,−y)



(x, y) =



f(x,y) −f(−x,y) +f(x,−y) −f(−x,−y)



(x, y) =



f(x,y) +f(−x,y) −f(x,−y) −f(−x,−y)



(x, y) =



f(x,y) −f(−x,y) −f(x,−y)+f(−x,−y)



(14)

As we know, the complex Fourier transform of a real 2D signal is formulated as

F(u,v)=



∞

−∞



∞

−∞

f(x,y)e

−i(ux+vy)

dx dy. (15)

According to the symmetry components in QFT and CFT, it is noted that the

quaternion Fourier kernel can be expanded into four individual oscillation terms:

264 Y. Xu et al.

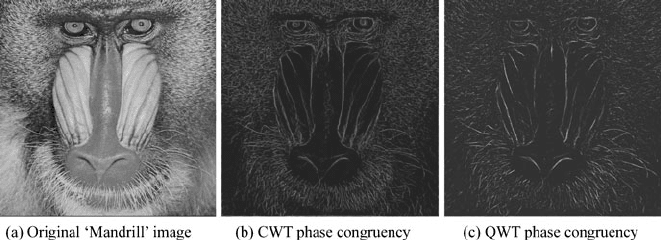
Fig. 11 The comparison of quaternionic phase congruency image and complex phase congruency

image

cosφ cos θ , −sinφ cos θ , −cosφ sin θ, and sin θ sin φ, which are combined into two

terms cos(φ +θ) and sin(φ +θ) in the complex Fourier kernel. As a result, we can

get four symmetrical components from QFT while two symmetrical components

from CFT of a 2D real signal. Therefore our quaternionic phase congruency func-

tion is deﬁned based on four symmetrical components, where the extreme value is

acquired only when both φ and θ are congruent across scales. However, complex

phase congruency is deﬁned based on two symmetry components which are com-

bined from the former four components, where the extreme value is acquired as

long as φ +θ are congruent across scales. So a tighter constraint is contained in

the quaternionic phase congruency model in contrast to the complex phase congru-

ency model. For good localization, we introduce the model of quaternionic phase

congruency to QWT, and, as an example, we compute the quaternionic phase con-

gruency image using a set of quaternion Gabors which are tuned to four scales and

six orientations. As shown in Fig. 11, only the features with higher local energy are

emphasized in the quaternionic phase congruency. By the way, we adopt Kovesi’s

idea [18] to impress the ill-effects of noises in quaternion domain.

Based on the quaternionic phase congruency model shown in (13), we propose a

wide-baseline stereo matching method as depicted in Fig. 12. In terms of the existing

afﬁne-invariant feature matching methods [17], the performance is affected domi-

nantly by the robustness of the extreme point/region detectors in the joint time–scale

space. Fortunately, the quaternionic phase congruency provides important clues for

such points/regions. According to Morron’s work, the extreme points of complex

phase congruency are consistent with the extreme points of local energy [19]. This

conclusion can be directly extended to quaternion Fourier domain due to the simi-

lar formulations in (12) and (15). The congruency of the quaternion phase vectors

also imply the reliability of the local structure in current successive scales. Hence,

we select the extreme points in the congruency image as the candidate features.

To capture more features at varied scales, we subsample the original image pair into

pyramidal structures. On each layer of the pyramid, we employ a set of quaternion

Gabors to obtain the phase congruency image, where the extreme-valued points are

assigned with the median scale of the given Gabor ﬁlter set as their characteristic

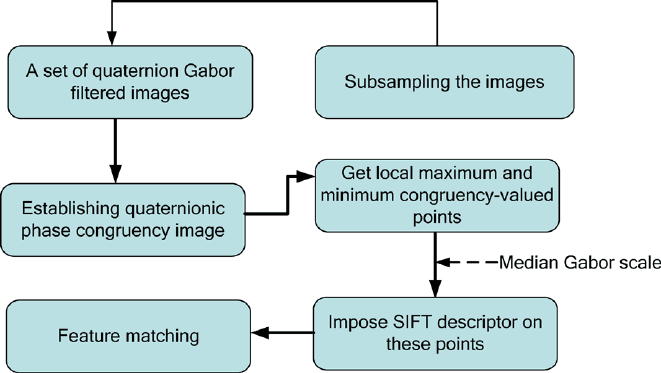
QWT: Retrospective and New Applications 265

Fig. 12 The wide-baseline matching scheme of invariant features obtained from quaternionic

phase congruency model

scales. The ratio of the maximum scale to the minimum scale is ﬁxed at 2 for each

Gabor set. Referring to the state-of-the-art of wide-baseline stereo matching meth-

ods, we use the best ranked SIFT descriptor [20] to match these features. In the

matching experiments, we even select the minimum scale of the given Gabor group

as the characteristic scales of the extreme congruency-valued points and ﬁnd that

the matching results are still encouraging under distinct afﬁne distortions, as shown

in Fig. 13(a). Here we only show nine point pairs for visual evaluation. In fact,

much more good matches can be obtained. To further testify our matching scheme,

we compute the fundamental matrix using the robust estimator in [21] based on the

matching results and demonstrate three corresponding epipolar lines, as shown in

Fig. 13(b).

A further issue which has to be considered is the afﬁne invariance of these feature

matching results. Since it is impossible to completely avoid outliers, here we exploit

the popular LMeds method [21] to remove them and reliably estimate the homogra-

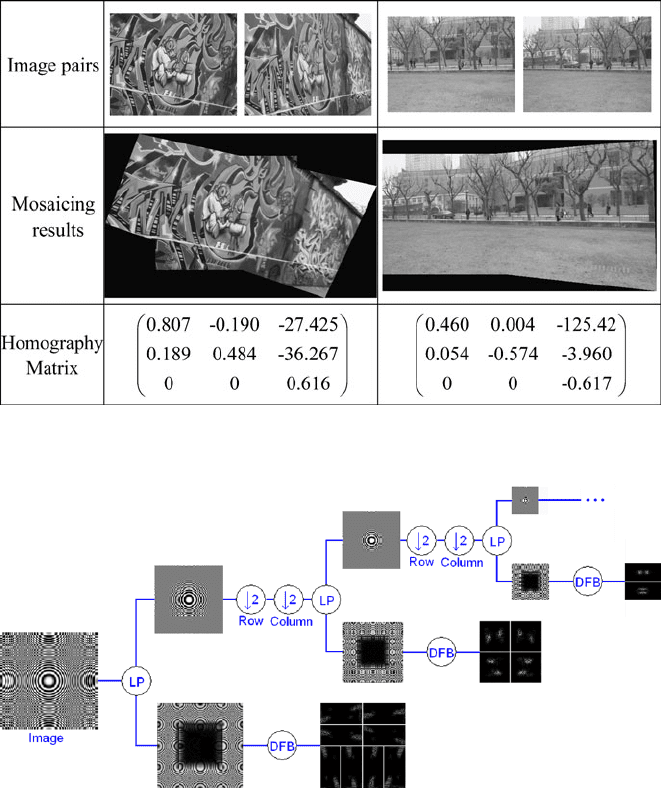
phy matrix between the corresponding points. Then we construct the mosaic images

based on homography matrices to do a visual inspection. Two image mosaicing tests

have been performed, and the related homography matrices are listed in Fig. 14.It

can be noticed that these homography matrices take into account projective distor-

tions (the nonzero values in the last entry).

5 The Potential Use of QWT in Image Fusion

As the tensor product of two separable shift-invariant CWTs, the quaternion wavelet

transform constructed in Sect. 2 is nearly shift-invariant. However, the separability

266 Y. Xu et al.

Fig. 13 The related matching results obtained by SIFT descriptor of the extreme phase-congruen-

cy-valued points in QWT domain

of QWT leads to bad directionality as shown in Figs. 1–3. In this section, we in-

troduce the directional ﬁlter bank (DFB) into QWT to get a better representation of

edges and textures.

It is known that contourlet transform (CT) provides features with high direction-

ality and anisotropy [22]. The architecture of CT is shown in Fig. 15, where the main

components are a Laplacian pyramid (LP) and a directional ﬁlter bank (DFB). The

LP decomposition at each step generates a sampled lowpass version of the original

and the difference between the original and the prediction, resulting in a bandpass

image. The process can be iterated on the coarse version. The DFB is designed

to capture the high-frequency components (representing directionality) of images.

Those bandpass images obtained in LP can be fed into DFB so that directional in-

formation can be captured efﬁciently. The architecture of CT allows for a different

number of directions at each scale. Thus, we can obtain a better representation of

edges and textures.

Since edges and textures are an intrinsic information in image representation, it

is important for QWT to enhance its directionality and anisotropy. Since QWT is

able to get multiscale bandpass images, we only introduce DFB in CT scheme into

QWT and observe what would happen then. To testify whether the hybrid transfor-

mation scheme “QWT +DFB” better localizes the high-frequency components, we

propose a new fusion method based on this hybrid transformation scheme, as shown

QWT: Retrospective and New Applications 267

Fig. 14 Two image mosaicing tests and corresponding homography matrices

Fig. 15 The architecture of CT

in Fig. 16, where IDFB and IQWT respectively denote the inverse DFB scheme and

the inverse QWT scheme.

A simple energy-based fusion method is adopted in the fusion tests, where the

larger coefﬁcients are preferred for generating the fusion result across scales except

that at the coarsest scale the coefﬁcients are averaged. The test images consist of

parts with different resolutions. The corresponding fusion results are illustrated in

Fig. 17. Due to the invertibility and near shift-invariance of QWT and DFB, the

proposed hybrid transformation scheme runs well in the image fusion task. It is dis-

tinct that the fusion results of “QWT + DFB” scheme represent the high-frequency