Bear H.S. Understanding Calculus

Подождите немного. Документ загружается.

Chapter

41 •

Line

Integrals

257

{'[(Sin

IH cos

26)(-

sin 6) +(sin 6cos 6)(cos 6)]d6

f'(-

sin

sin 6 cos

26)

[COS

6-+COS

6]:

-1

+ +-

-+)=

-2

+ j =

-~.

If a forcefield is definedin space,sayby

F(x,y, z)

= u

(x,y, z) i +u

(x,y, z) j +u

(x,y, z) k,

then the line integralof F . ds overa spacecurve C has the form

F , ds =1u1(x,y,z) dx +u

2(x,y,

z) dy +u

3(x,y,

z) dz.

c c

If the curvehas parametric equations

=f(t) , y =g(t),

z = h(t),

t -s b,

thenthe integralis evaluated by substituting f(t) , g(t), and h(t) forx,y, andz

respectively,

and

replacing the differentials

dx,

dy, dz byf'(t)dt, g'(t)dt, h'(t)dt.

EXAMPLE

41.3

Find

foF·

where

C isthe

helix

x =

cos

t,y

= sint, Z = t,

for

0 -s t -s

211',

and

F(x,y, z) = xy i +y j +yz k.

Solution

Here

dx =-sin t dt, dy =

cos

t dt,

and

dz = dt, so

( F . ds = 1

(cos

t sin

t)(-

sint) dt + 1

sin t cos t dt +

f1T

t sin t dt

0 0 0

sin

t]27T+

sirr'

21T

+[-t cos t +sin

3 0 2 0

-211'.

given

curve

C can be

parameterized

any

number

ways.

For

example,

the

arc

of the

parabola

y =x

from (0, 0) to (1, 1)can be parameterized by any of thesepairs of equations:

(41.6)

(41.7)

(41.8)

-1

o~ t

y = sin

y =(t +

1)2,

x = sin t,

x = t + 1,

x=t,

(i):

(ii):

(iii):

O~t~

11'.

Tocalculatea line integraloverC any of these parameterizations can be used,and indeedany

parameterization which traces the curve out in the directionfrom (0, 0) to (1, 1). Changing

the parameterization is the same as changingthe variable in the integral.

Two

parameteriza-

tions whichtrace out the curvein the same directionwill givethe same

answer,

and parame-

terizations which trace the curve out in oppositedirections will give

answers

that are nega-

tivesof each

other.

258 Understanding Calculus

EXAMPLE

41.4

Let P(x, y) = x + y. Calculatef

eP(x,

y) dx for parameterizations (41.6) and (41.8) of the parabolicarc

from(0, 0) to (1, 1).Thenparameterize the samearc in the oppositedirection,call that

-C,

and evaluate

f_eP(x,y)

dx.

Solution

Forthe parameterization (41.6), we have

1(x +y) dx = I

+ tl) dt

c 0

..!-tl

..!-

t3]1

2 3 0

115

=2+3=6·

Fortheparameterization

(41.8)

weget

7T/2

(x + y) dx = (sin t + sirr' t)(cos t) dt

C 0

1 1

]7T/2

= - sin

t + - sin

2 3 0

115

=-+-=-

2 3

6·

Hence

Wecan parameterize

-C

for instanceby

x=I-t,

y=(I-t)2,

o-s t -s 1.

(x+y)dx=

f[1-t+(I-t)2](-dt)

-c

- t) - (1 - t)2]dt

1 2 1

3]1

1 1 5

-(I-t)

+ -

(I-t)

=--

- -

=--

2 3 0 2 3

6·

PROBLEMS

Findthe integralfeF . ds for the givenfunctionF and the givencurve C.

41.1 F(x, y) = y i + x j; C is the segmentfrom (0, 0) to (1, 1).

41.2

F(x,y)=(x+y)j;

Cis

the segmentfrom (0,

l)to(I,O).

41.3

F(x,y)

= i - j; C is the arc of the parabolay

from

(-1,1)

to (1,1).

41.4 F(x, y) =(x +y) i +(x - y) j; x =tl,y =t + 1, 1 -s t -s 2.

Evaluatethe line integrals.

41.5 f

+y)2 dx; C is the segmentfrom (1, 1) to (3, 1).

41.6 feXY dy; C is the segmentfrom (1,0) to (1, 1).

41.7

fex

dy; C is the boundaryof the rectangle, {(x, y) : 0 -s x :s; 2, 0 -sy -s I}, traced out

counterclockwise; i.e., C consistsof the four segments: (0, 0) to (2, 0), (2, 0) to (2, 1), (2,

to (0, 1), and (0, 1) to (0, 0).

41.8

feY

dx; C is the boundary of the top half of the unit circle, traced out counterclockwise,

i.e., C consists of the segmentfrom (-1, 0) to (1, 0), followed by the top half of the unit

circle from (1, 0) to (-1, 0).

Green's

Theorem

There is a

remarkable

(and useful) relationship

between

a line integral around a boundary

curve,

anda

double

integral overthe regionbounded by the

curve.

Herewe dealwithclosed

curves, in whichthe starting and

ending

points are the

same.

Boundary

curves

are simple

closed curves, whichmeansthe curve does not intersect itself exceptat the beginning and

ending

point.

(Figure

42.1.)

Closed

curve

Simple

closed

curve

(42.1)

Figure 42.1

Any

simple

closedcurve

divides

theplaneintotwodisjoint regions-the insideandthe

outside.

will

always

orientsuch a curve in the

positive

(counterclockwise) direction, so

the

inside

region

always

lies on the left sideas youproceedalongthe

curve.

LetP(x,y) and Q(x,y) be

functions

definedon a

simple

closedcurveC and the region

R bounded by C.WithC oriented in the

positive

direction, the

following

twoidentities

hold:

fcP(x,y)dx=

-Py(x,y)dA,

Q(X,y) dy=

Qx(x,y)dA,

(42.2)

Thelittlecirclethrough the integral signindicates that C is a

simple

closed

curve,

andhence

259

260

Understanding Calculus

a boundary

curve.

The identities (42.1)and

(42.2)

can be combined in a singleequation, and

this is called

Green's theorem:

fcp(x,y)

dx+ Q(x,y) dy= JL(Qx(X,y)

-Pix,y))

dA.

(42.3)

Noticethat (42.3)impliesboth (42.1)and (42.2)sincewe can let P(x, y) or Q(x, y) be identi-

callyzeroin

(42.3).

EXAMPLE

42.1

Let R be the part of the disc x

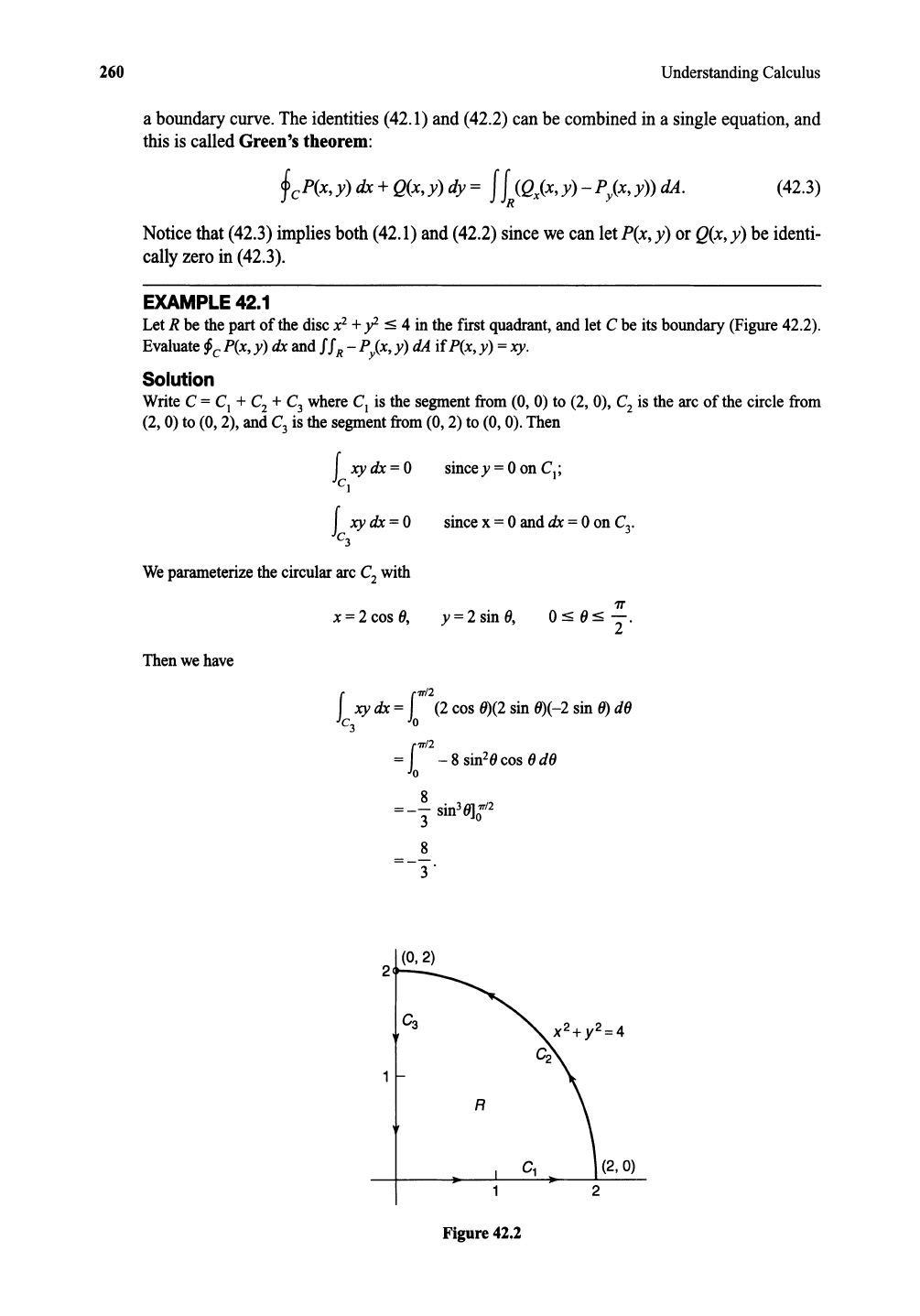
+ y -s 4 in the first quadrant, and let C be its boundary(Figure42.2).

Evaluate

~cP(x,y)

dx and

-Py(x,y)

dA if

P(x,y)

= xy.

Solution

Write C = C

+ C

where C

is the segmentfrom (0, 0) to (2, 0), C

is the arc of the circle from

(2, 0) to (0, 2), and C

is the segmentfrom(0, 2) to (0, 0).Then

i xydx=O

sincey=OonC};

i xy dx = 0 since x = 0 and dx = 0 on C

Weparameterize the circulararc C

with

x = 2 cos 8, y = 2 sin 8,

Thenwe have

11'

o-s 8 -s

'TT'

xy dx = (2 cos 8)(2sin 8)(-2 sin 8)d8

'TT'

= 0 - 8 sin

cos 8d8

sin381

71'/2

=-"3.

(0,2)

(2,0)

Figure 42.2

Chapter

42 •

Green's

Theorem

Therefore

cX)'

dx =fX)' dx + f X)' dx +f X)' dx

C C

8 8

= 0 - -

+0=--

3·

261

Forthe

double

integral

have

will

verify

the

Green's

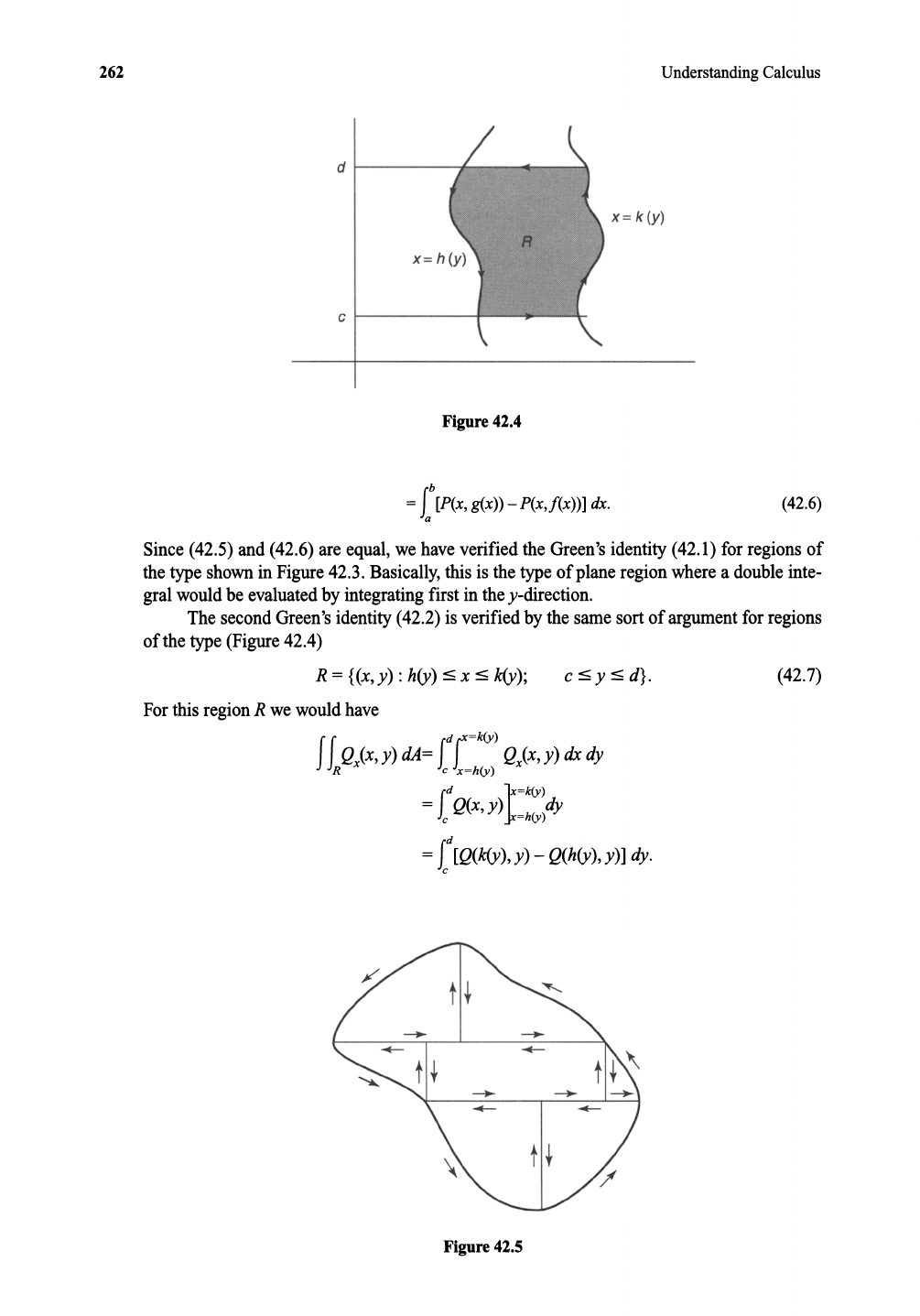
identity (1) forthe

region

between

two

curves

y = g(x) and

= f(x), for a :::x ::: b

(Figure

42.3):

R={(x,y):g(x):::y:::f(x); a:::x:::b}.

(42.4)

The

double

integral is calculated as

follows:

-p (x,y) dA =

(bf

Y=f(

X) - P (x,y) dy dx

R Y J

y =g(x ) y

= (b _ P(x,

=f(

p=g(

= r[-P(x,f(x» +P(x,g(x»] dx.

(42.5)

Forthe line integral, the curve C

comes

in four pieces-the

lower

and uppergraphsof g(x)

andf(x), and the twovertical

segments

on the linesx = a andx = b. The

integrals

on the ver-

tical

segments

are both zero, since if x = constant, dx = O. On the

lower

curvewe integrate

from

a to b, andon the uppercurve

from

b to a. Thus

TcP(x

,y)

dx=

(P(x,

g(x»

dx+ (P(x,f(x» dx

Figure 42.3

262 Understanding Calculus

f------f---'''''--

.-\

f------

...........

~+-

Figure 42.4

([p(x

,g(X))-P(x,f(x))] dx.

X =

(42.6)

Since(42.5) and (42.6) are

equal,

wehaveverifiedthe

Green's

identity(42.1)for regions of

the type

shown

Figure

42.3.

Basically,

this is the type of planeregion

where

double

inte-

gralwouldbe

evaluated

by integrating first in they-direction.

The

second

Green's

identity

(42.2)

is verifiedby the samesort of

argument

for

regions

of the type

(Figure

42.4)

R = {(x,y) :

heY)

s x s k(y); c s y s d}.

(42.7)

Forthis

region

R wewouldhave

-k(y)

ffQ

x(x,

y) dA=J -

Q/x

,y) dx dy

R e

~h(y)

=k(y)

= e Q(x,y)

.lx

=h(y)dy

([Q(k(y),y)

- Q(h(y),y)] dy.

Figure 42.5

Chapter42 • Green's

Theorem

263

Thelast

formula

above

is the sameas

cQ(x, y) dy sinceonceagainthe integrals on the line

segments

(herey =constant) are

zero.

Figure

42.5

shows

how a

general

region can be

divided

up into subregions each of

whichcanbe considered as eitherthe type of

(42.4)

(42.7).

That is, in the

subregions

one

couldintegrate either

y or x first, so

(42.1)

and

(42.2)

bothhold in each

subregion.

The inte-

grals overthe interior

segments

all

cancel,

so the sum of the integrals aroundthe

subregions

isjust the integral aroundthe boundary of the

whole

region.

EXAMPLE

42.2

Calculate

1- x

)

dy and ffR

-Ix

(1- x

)

dA whereR is the right sideof the unit disc,

R = {(x,y) : x

+ r -s 1,x

O},

and C is its boundary

(Figure

42.6).

Solution

Letx = cos

(],

y = sin

(],

-s (]-s

forthe halfcircle,andx = 0 on the

segment

from(0, 1)to (0,-1).

(1 - x

)

dy = I

7r/2

(1 - cos

26)cos

(Jd(J +

I-I

1dy

j C -7T/2 I

= I

7r/2

sin

(Jcos

(Jd(J

y]-I

-m2

1 ]7T/2

= - sin

(]

+(-1 - 1)

3 -7T/2

1 2 4

3(1-(-1))-2

= 3

-2

=-3'

The areaintegral is

III~~

-(I-x

)

dA = - 2xdx dy

-I

]~~

-x

-I

x=O

I 1

= - (1 - r)dy =

-y

+ - I

-I

1 (

2 2 4

=-1+

+1-

=-3-3=-3·

x=cos

()

y=sin(}

_1I<(}<1I

2 - - 2

-1

Figure 42.6

264

Understanding

Calculus

If P(x, y) =

-y

Green's

theorem,

so-Py(x, y) = 1,then

fe - Y dx =fLIdA =area

This

shows

howareacanbe calculated as a lineintegral aroundthe

boundary.

Thereis a similar

formu-

la usingQ(x,y) =x, so

Qx(x,

y) = 1, and

feX dy =fLIdA =area

EXAMPLE

42.3

Usethe

formula

- y dx =ff

dA to find the area of the ellipsef+ f = 1.

Solution

Wecanparameterize the curveby

x = 3 cos 8, y = 2 sin 8,

Then

fe - Y dx =f',r(-2 sin 0)(-3

sin.O)

'77

1- cos 28

= 6 d8

o 2

[

]271'

= 3 8-

sin 28 0

= 3[(21T- 0)-

I(O

-0)] =

61T.

EXAMPLE

42.4

Calculate

c[x

log(x

+ 1)- y] dx

where

C is the unitcircle,andR is the disc

+1 s 1.

Solution

Since

a a

- Oy

(x21og(x2

+ 1)- y) =- Oy(-y) = 1,

the termx

log(x

+ 1) adds

nothing

to the integral, whichis the sameas

The

message

Example

4 is thatforany

simple

closedcurveC,

cf(x)

dx=fcg(y) dy =

So,for

example,

fc (I(x) +

g(y»

dx= fcg(y)

dx,

and

fc (I(x) +

g(y»

dy = fc f(x) dy.

It is important to keepin mindthat in all these

examples

C is a

simple

closed

curve,

andnot

just any

curve.

Chapter42 • Green'sTheorem

265

EXAMPLE

42.5

Evaluate

cos-r + x

) dx where C is the boundaryof the rectangle with comers at (3, 1), (6, 1),

(6, 2), (3, 2).

Solution

Westart with the observation that

On the verticalsegments

dx = 0, so

fr'1

dx +

J:ry2dx

1 4

-(6

) +

-(3

)

3 3

-6

= -189.

It is easy to check(Problem 13)that

y dA= -189.

1.0

-1.0

Figure 42.7

266 Understanding

Calculus

PROBLEMS

Evaluate

the integrals

~cP(x,

y) dx and

Py(x,

y) dA for the

following

regions

R and their

boundary curvesC.

42.1

P(x,y)

y2;

R =

{(x,y):

=5 I}.

42.2 P(x,y)

+y;

R={(x,y):y=51-x2,y~0}.

42.3 Pix,y) =xy; R is the tophalfof the ellipse

= 1;(x =3 cos

fJ,

y =2 sin

fJ).

Evaluate

~cQ(x,

y) dyand f f R

Qx(x,

y) dA for the

following.

42.4 Q(x,y) =x

+y; R is the unit

square

R = {(x, y) : 0 =5x =5 1,0 =5Y =5 I}.

42.5

Q(x,y) =x; Cis the ellipsef+f = 1.

42.6

Q(x,y) = x

siny; R is the

square

withvertices (0, 0), (!, 0), (!, !), (0, !).

42.7

Evaluate

~cx

dy whereC is the boundary of the triangle withverticesat (0,0), (1, 0), and

(1, 1).

(Since

the integral is the area,your

answer

shouldbe

~.)

42.8 Usethe factthat

dy = area ofR to find withoutcalculation the valueof

dy where

C is the circle

(x - 2)2+(y +3)2= 5.

42.9 Find

~dYeY

+xy)dy

where

C is the circlex

= 4.

42.10 Findtheareaboundedby the parabolay

= 4

-x

andthex-axisas a lineintegral

~cx

dy.

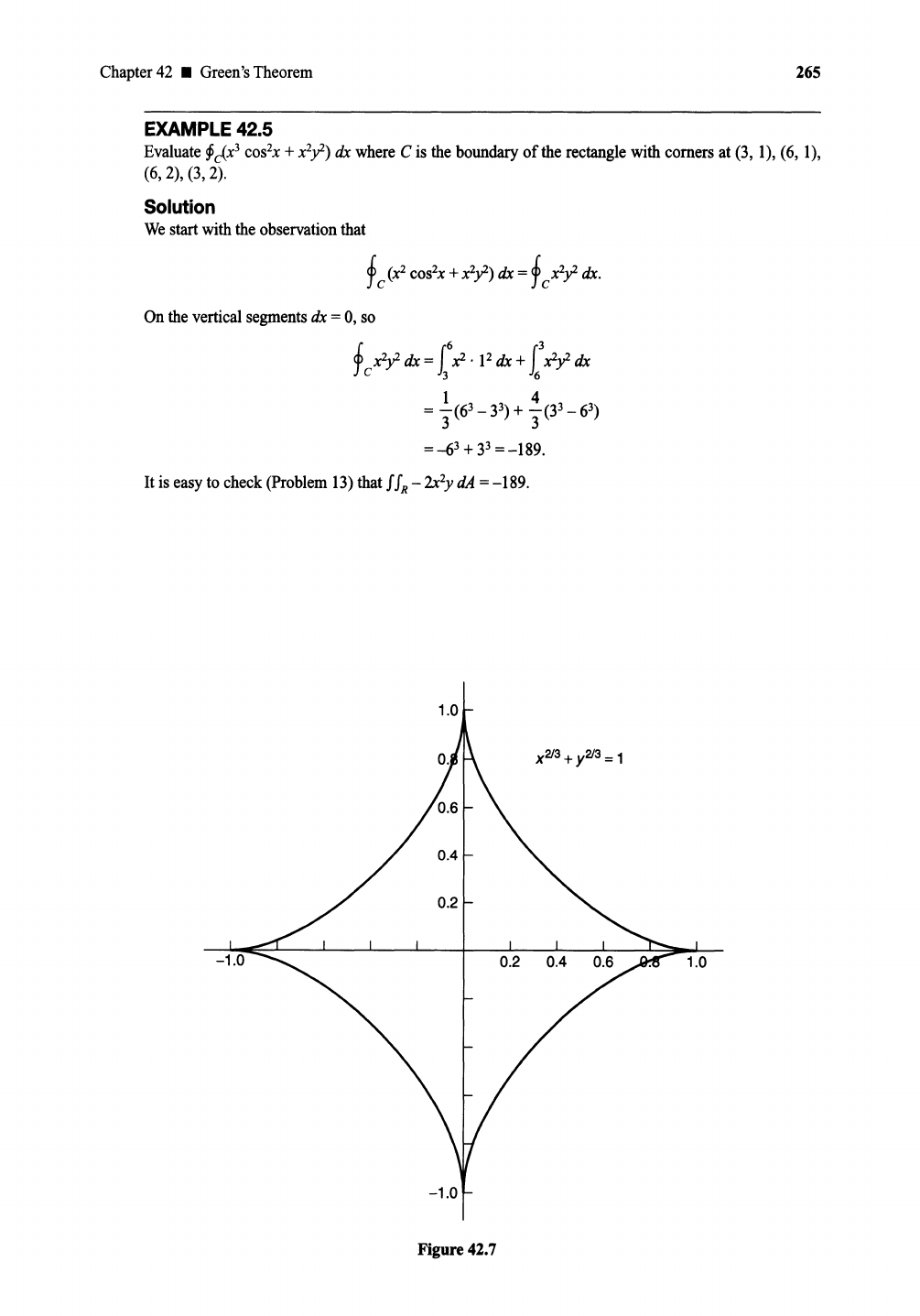
42.11 Find the area insidethe curve

(Figure

42.7)X

2/3

y2/3

= 1 as a line integral. Hint: Show

that

x =cos

3fJ,

Y = sin

3fJ,

0 =5

217",

is a parameterization, anduse

f~1T

cos

4fJ

sin

2fJ

dfJ

f~1T(1

+cos

2fJ

--cos

22fJ

- cos

32fJ)

dfJ.

Noticethat

(217'

cos

2fJ

dfJ

= 0;

(217'

cos

32fJ

42.12 Findthe areaunderone arch of the cycloidx =

- sin

fJ,

y = 1 - cos

fJ,

0 =5

271'

and

overthex-axis

(y =

0,0

=5x =5

271').

Checkthe orientation of your

curve.

42.13 Checkthatthe areaintegral in

Example

5 equals-189.