Безруков А.Б., Саитгараев С.С. Прикладная теория игр
Подождите немного. Документ загружается.


61
Состояние среды
Вариант
системы А
i
В
1
В
2
...
В
j
...
В
m
А
1
C
11
C
12
...
C
1j
...
C
1m
А
2
C
21
C
22
...
C
2j
...
C
2m
... ... ... ... ... ... ...
А
i
C
i1
C
i2
...
C
ij
...
C
im
... ... ... ... ... ... ...
А
n
C
n1
C
n2
...
C
nj
...
C
nm
Требуется с проектировать такую систему, которая обеспечивает
минимальные затраты, то есть:
– вычислить ожидаемые затраты для каждой системы A
i
(i = 1, 2,..., n), используя априорное распределение;
– выбрать систему с наименьшими затратами.
Возможны две ситуации:
1) известно априорное распределение вероятности состояния
среды P(B=B
j
). На начальных этапах проектирования систем проекти-
ровщик может иметь некоторую информацию о среде или интуитивно
догадываться на основании проектирования предыдущих систем о ве-
роятностных параметрах среды, т.е. проектировщик имеет дело с ап-
риорной информацией.
Затраты вычисляются по форм уле
)n,1i(,))BB(PC()B;A(С
m
1i
j
ijji
=
∑
=⋅=
−
(3.7)
2) исследователь не имеет информации о состоянии среды, но
он имеет или может получить дополнительную информацию по тому
или иному косвенному параметру среды, в которой предполагается
работать системе. При этом бывают известны:
B – случайная переменная, характеризующая состояние среды;
Х – случайная переменная, связанная так или иначе с перемен-
ной B;
P(B
j
) – aприорное распределение В
j
;
Q(x B=B
j
) – условное распределение переменной B при Х= х.
Для определения оптимальной системы требуется найти услов-
ное распределение переменной В при Х= х. Распределение H(B
j
X=x)
называется апостериорным распределением пер еменной B, которое
получено на основании известной информации о переменной Х.
Для определения апостериорной вероятности можно использо-
вать формулу Байеса, которая связывает априорную и апостериорную
вероятности:

62
∑
⋅==
⋅=
==
=
m
1k
kk
jj
i
))B(P)BBx(Q(
)B(P)BBx(Q
)xXB(H
. (3.8)
Затраты для каждой системы в этом случае будут равны:
)n,1i())xXB(C()B;A(С
m
1j
iijji
=
∑
==
=
(3.9)
Окончательно можно представить следующий алгоритм дейст-
вия исследователя при наличии дополнительной информации.
А. Имея таблицу затрат (табл. 3.1), априорное распределение
P(B
j
) (j=1, m), определить по формуле (3.7) ожидаемые затраты для
каждой системы для различных состояний среды, выбрать систему,
имеющую наименьшие затраты.
Б. Если априорное распределение неизвестно, то по условному
распределению переменной X для данного состояния среды B = B
j
, т.е.
Q(x B=B
j
), необходимо:
а) определить апостериорное распределение переменной В по
формуле (3.8);
б) получить надежное значение случайной переменной X, ска-
жем, x;
в) вычислить ожидаемые затраты для каждой системы, ис-
пользуя апостериорное распределение H(B
j
X=x) по формуле (3.9);
г) выбрать систему, имеющую минимальные затраты.
Для определения оптимальной системы в условиях неопреде-
ленности с исходной информацией о среде и без нее целесообразно
использовать ЭВМ, которая значительно ускоряет процесс поиска оп-
тимальной системы.
3.4. Приложения игровых методов
в теории статистических решений
Пример 3.2. Существует предприятие, которое занимается вы-
пуском новой продукции. Ввиду ограниченности ресурсов предпри-
ятие может заниматься только одним видом деятельности, т.е. не име-
ет возможности одновременно заниматься двумя и более задачами.
Возникает проблема: заниматься НИОКР, т.е. разработкой новой про-
дукции (НП), либо модернизацией уже выпускаемой.
Срок разработки t
p
новой продукции заранее неизвестен и мо-
жет составлять 5, 10 или 15 лет. Это – “стратегия” приро-
ды:
3
23p
2
22p
1
21p
x15t,x10t,x5t →=→=→=
.
Эффект от деятельности оценивается в 15-летнем интервале
планирования: T=15. ЛПР (руководство предприятия) имеет 2 страте-
63
гии:
1
1
x
– проводить НИОКР,
2
1
x
– не проводить НИОКР, т.е. ограни-
читься модернизацией.
Требуется оценить целесообразность того или иного решения
пользуясь критериями Вальда, Сэвиджа, Гурвица при L=0,4, Байеса
при априорных вероятностях состояний природы η
1
=0,2, η
2
=0,45,
η
3
=0,35, а также найти равноэффективное значение параметров x.
Исходные данные для решения игровой задачи представлены в
табл.3.2.
Таблица 3.2
Исходные данные (млн р./г.)
Затраты на
НИОКР и
внедрение
Эффект от но-
вой продукции
Затраты на мо-
дернизацию
Эффект от
модерниза-
ции
С
н
=2,4 Э
н
=14 С
м
=1,2 Э
м
=2,6
Расчет затрат и экономического эффекта в интервале планиро-
вания целесообразно представить в форме ситуационной таблицы
(табл. 3.3), для чего вначале составляется графовая модель:
а) новая разработка длится 5 лет
НИОКР Модернизация и эксплуатация
5 10
б) новая разработка длится 10 лет
НИОКР Модерн. и экспл.
105
в) новая разработка длится 15 лет
НИОКР
15
в) новая разработка не ведется
Модернизация и эксплуатация
15
На основании табл. 3.3 составим матрицу H выигрышей ЛПР.
Элементы матрицы h
ij
вычисляется по формулам:
h
1j
=-C
м
·t
pj
+(Э
н
-С
м
+Э
м
)·(T-t
pj
), h
2j
=(С
м
+Э
м
)·T
−
=
212121
3653142
H
Оценим целесообразность стратегии ЛПР по критерию Вальда:
2,1i
ij
1,3j
2,1i
maxhmin maxWa
=
=
=
==
(-36; 21;)=21;

64
i
*
=arg Wa=2, т.е. целесообразна стратегия
2
1
x
.
Таблица 3.3
Возможные ситуации
Продол-
житель-
ность
разра-
ботки t
pj
Затраты
на
НИОКР
и вне-
дрение
Эффект
от новой
продук-
ции
Затра-
ты на
мо-
дерни-
зацию
Эффект
от мо-
дерниза-
ции
Суммар-
ный эко-
номиче-
ский эф-
фект
Стратегия
ЛПР
лет (млн р.) (млн р.) (млн р.) млн р.) (млн р.)
5-12 140 -1226 142
10 -24 70 -6 1353
Проводит-
ся НИОКР
1
1
x
15 -36 0 0 0 -36
000-1839 21
000-1839 21
Не прово-
дится
НИОКР
2
1
x
000-1839 21
Оценим целесообразность стратегии ЛПР по критерию Сэвид-
жа, для чего составим матрицу рисков:
ijij
i
ij
hhmaxr −=
=
032121
5700
R
2,1i
ij
1,3j
2,1i
minrmax minSa
=
=
=
==
( 57; 121)=57;
i
*
=arg Sa=1, т.е. целесообразна стратегия
1
1
x
.
Оценим целесообразность стратегии ЛПР по критерию Гурвица
L=0,4:
2,1i
ij
3,1j
ij
3,1j2,1i
max)hmin6,0hmax4,0(maxHu
=
=
==
=+=
(0,4⋅142+
+ 0,6⋅(-36)=35,2; 0,4⋅21+0,6⋅21=21)=35,2;
i
*
=arg Hu=1, т.е. целесообразна стратегия
1.
Значение параметра L для равноэффективных решений ЛПР
(критическое значение L) может быть найдено из уравнения:
L·h
11
+(1-L)h
13
=Lh
21
+(1-L)h
23
,
так как
2321j1
3,1j
13j1
3,1j
11
hиh,hminh,hmaxh
=
=
==
находятся в тех же
столбцах, что и h
11
и h
13
соответственно.

65
Итак
:
L·142+(1-L)(-36)=L21+(1-L)21, 178L=57, L
кр
=0,32.
Оценим целесообразность стратегии ЛПР по критерию Байеса
при априорных вероятностях состояний природы, характеризующих
неопреде ленность ситуации, равных: η
1
=0,2, η
2
=0,35, η
3
=0,35:
2,1i
3
1j
ijj
2,1i
maxhmaxBa
=
=
=
∑
=η=
(142⋅0,2+53⋅0,45-36⋅0,35=39,65;
21⋅0,2+21⋅0,45+21⋅0,35=21)=39,65;
i
*
=arg Ba=1, т.е. целесообразна стратегия
1
1
x
.
Сопоставляя результаты оценок по всем примененным критери-
ям, ЛПР может сделать вывод о целесообразности проведения НИОКР.
Пример 3.3. Возможно строительство четырех типов электро-
станций: A
1
(тепловых), A
2
(приплотинных), A
3
(бесшлюзовых) и A
4
(шлюзовых). Эффективность каждого из типов зависит от различных
факторов: режима рек, стоимости топлива и его перевозки и т.п.
Предположим, что выделено четыре различных состояния, каждое из
которых означает определенное сочетание факторов, влияющих на
эффективность энергетических объектов. Состояния природы обозна-
чим через P
1
, Р
2
, P
3
и Р
4
. Экономическая эффективность строительства
отдельных типов электростанций изменяется в зав исимости от состоя-
ний природы и задана матрицей
=
8241
10358
12432
4825
A
Cогласно критерию Вальда
3)1;3;2;2max(aminmax
ij
j
i
==
следу-
ет выбрать решение А
3
, т.е. предусмотреть строительства бесшлюзо-
вой ГЭС.
Воспользуемся критерием Сэвиджа. Построим матрицу рисков:
=
4617
2500
0426
8033
R
Покажем, например, как были получены элементы первого
столбца матрицы R. Имеем mах a
11
= a
31
= 8, поэтому r
11
= a
31
– a
11
= 3,
66
r
21
= a
31
– a
21
= 6, r
31
= а31 – a
31
= 0, r
41
= а
31
– а
41
= 7. Согласно крите-
рию Севиджа определяем
5}7;5;6;8min(rmaxmin
ij
j
i
==
.
В соответствии с этим критерием также предполагается реше-
ние Аз – строительства бесшлюзовой ГЭС.
Воспользуемся критерием Гурвица. Положим L = 0,5; тогда
{
7)5,4;5,6;7;5(max}amin)L1(amaxLmax
ij
j
ij
ji
==−+⋅
,
то есть следует принять решение А2 – строительство приплотинных
ГЭС.
Рассмотрим принцип Байеса-Лапласа. Если предположить из-
вестным распределение вероятностей для различных состояний при-
роды, например считать эти состояния равновероятными (q1 = q
2
= q
3
=
= q
4
= 1/4), то для принятия реше ния следует найти математические
ожида ния выигрыша:
4
3
4
4
1
4
4
1
8
4
1
2
4
1
5M
1
=⋅+⋅+⋅+⋅=
4
3
5
4
1
12
4
1
4
4
1
3
4
1
2M
2
=⋅+⋅+⋅+⋅=
4
3
6
4
1
10
4
1
3
4
1
5
4
1
8M
3
=⋅+⋅+⋅+⋅=
4
3
3
4
1
8
4
1
2
4
1
4
4
1
1M
4
=⋅+⋅+⋅+⋅=
Так как максимальное значение имеет Мз, то следует выбрать
решение Аз – строительство бесшлюзовой ГЭС.
67
4. МЕТОДЫ РЕШЕНИЯ
НЕКОТОРЫХ БЕСКОНЕЧНЫХ ИГР
Бесконечной называется игра, в которой, по крайней мере, одна
из сторон имеет бесконечное множество стратегий. Общие методы
решения таких игр еще мало разработаны. Однако для практики могут
представлять интерес некоторые частные случаи, которые допускают
сравнительно простое решение.
Рассмотрим игру двух игроков А и В, каждый из которых имеет
бесконечное (несчетное) множество стратегий; эти стратегии для иг-
рока А соответствуют различным значениям непрерывно меняюще-
гося параметра х, а для игрока В – параметра y. В данном случае вме-
сто матрицы [ а
ij
] игру определяе т некоторая функция двух непре-
рывно меняющихся аргументов а(х,у), которую мы будем называть
функцией выигрыша (заметим, что сама функция а(х,у) необязательно
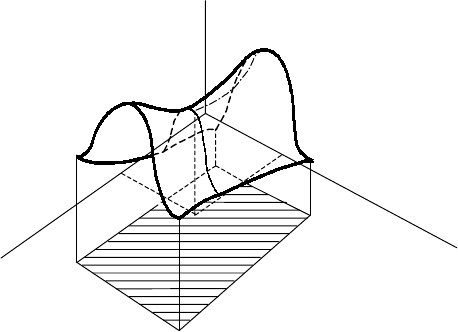
должна быть непрерывной). Функцию выигрыша а(х,y) можно пред-
ставить геометрически некоторой поверхностью а(х,у) над областью
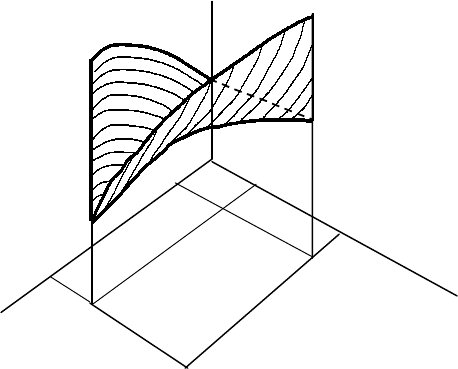
изменения арг ументов (х,у) (рис. 4.1).
Рис. 4.1
Анализ функции выигрыша а(х,у) производится аналогично
анализу платежной матрицы. Сначала находится нижняя цена игры α;
для этого определяется для каждого х минимум а(х,y) ф ункции а (х,y)
по всем у:
;)y,x(amin
y
i
=α
затем ищется максимальное из этих значений по всем х (максимин):
0
x
1
a(x,y)
x
2
y
y
1
x
y
2
68
)y,x(aminmax
y
x
=α
Верхняя цена игры (минимакс) определяется аналогично:
)y,x(amaxmin
x
y
=
β
Рассмотрим случай, когда α=β.
Так как цена игры ν всегда заключена между α и β, то общее их
значение и есть ν.
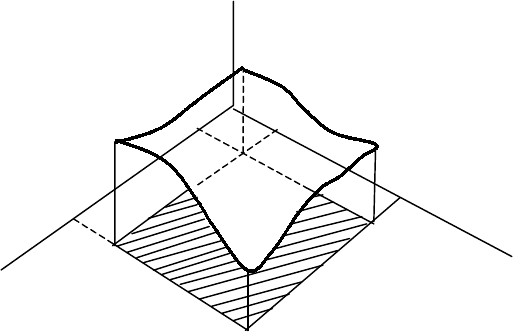
Равенство α=β означает, что поверхность а(х,у) имеет такую
точку с координатами x
o
, y
o
, в которой а(х,у) является одновременно
минимальным по у и максимальным по х (рис. 4.2), т.е. седловую точ-
ку.
Рис. 4.2
Значение а(x,у) в этой точке и есть цена игры ν: ν = а(x
o
,у
o
).
Наличие седловой точки означает, что данная бесконечная игра
имеет решение в области чистых стратегий; x
o
, y
o
представл яют собой
оптимальные чистые стратегии игроков А и В.
В общем случ ае, когда α≠β, игра может иметь решение только в
области смешанных стратегий (возможно, не еди нственное).
Смешанная стратегия для бесконечных игр есть некоторое рас-
пределение вероятностей для стратегий x и у, рассматриваемых как
случайные величины.
Это распределение может быть непрерывным и определяться
плотностями f
1(x)
и f
2(y)
; может быть дискретным, и тогда оптимальные
x
o
a(x,y)
y
y
o
x
0
69
стратегии состоят из набора отдельных чистых стратегий, выб ираемых
с какими-то отличными от нуля вероятностями.
В случае, когда бесконечная игра не имеет седловой точки,
можно дать наглядную геометрическую интерпретацию нижней и
верхней цене игры. Рассмотрим бесконечн ую игру со стратегиями х,у,
заполняющими непрерывно отрезки осей (х
1
,х
2
) и (у
1
,у
2
) и с функцией
выигрыша а(х,у), представленной геометрически поверхностью, при-
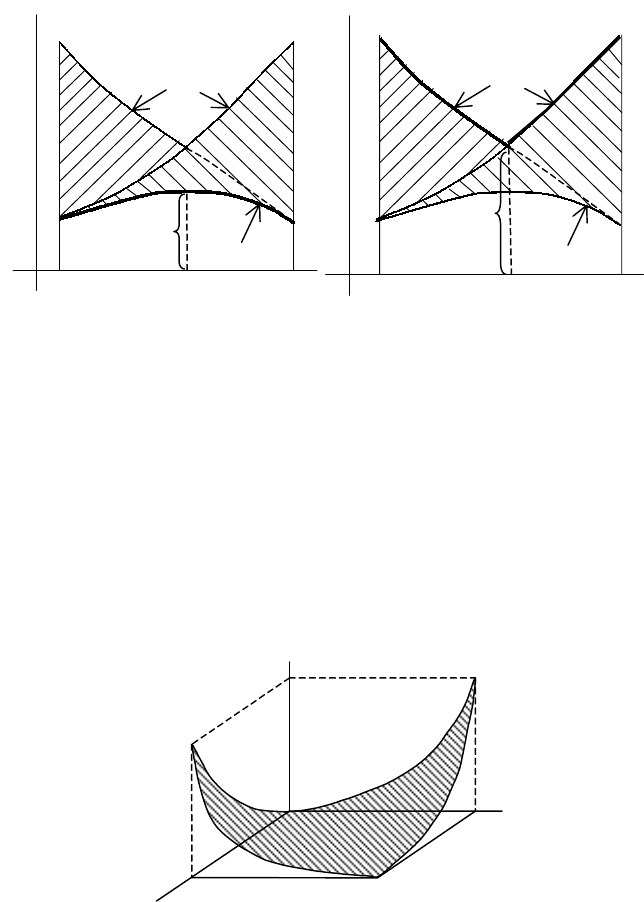
веденной на рис. 4.3.
Рис. 4.3
Чтобы определить нижнюю цену игры α, нужно поверхность
а(х,у) спроектировать на плоскость х0а (рис. 4.4,а). Получим некото-
рую фигур у, ограниченную с боков прямыми х=х
1
и х=х
2
, а сверху и
снизу – кривыми Кв и Кн. Нижняя цена игры α, очевидно, есть не что
иное, как максимальная ордина та кривой Кн. Аналогично, чтобы най-
ти верхнюю цену игры β, ну жно поверхность а(х,у) спроектировать на
плоскость у0а и найти минимальную ординату верхней границы Кв
проекции (рис. 4.4,б).
0
x
1
a(x,y)
y
y
1
x
y
2
x
2
70
а) б)
Рис. 4.4
Рассмотрим один элементарный пример бесконечной игры.
Пример 4.1. Игроки А и В имеют каждый множество возмож-
ных стратегий х и у, причем 0 ≤ x ≤ 1 , 0≤ y ≤ 1. Функция выигрыша
задана выражением а(х,у) = (х – у)
2
. Найти решение игры.
Решение. Поверхность а(х,у) представляет собой параболиче-
ский цилиндр (рис. 4.5) и не имеет седловой точки. Определим ниж-
нюю цену игры; очевидно,
0)y,x(amin
y
=
для всех х, отсюда
.0)y,x(aminmax
y
x
==α
Определим верхнюю цену игры. Для этого при
фиксированном у найдем
.)yx(amin
2
x
−
1
0 1
1 x
2
1
y
Рис. 4.5
a(x,y)
а
0
α
Кн
Кв
x
1
x
2
β
а
0
Кн
Кв
x
1
x
2
