Bhushan B. Handbook of Micro/Nano Tribology, Second Edition

Подождите немного. Документ загружается.

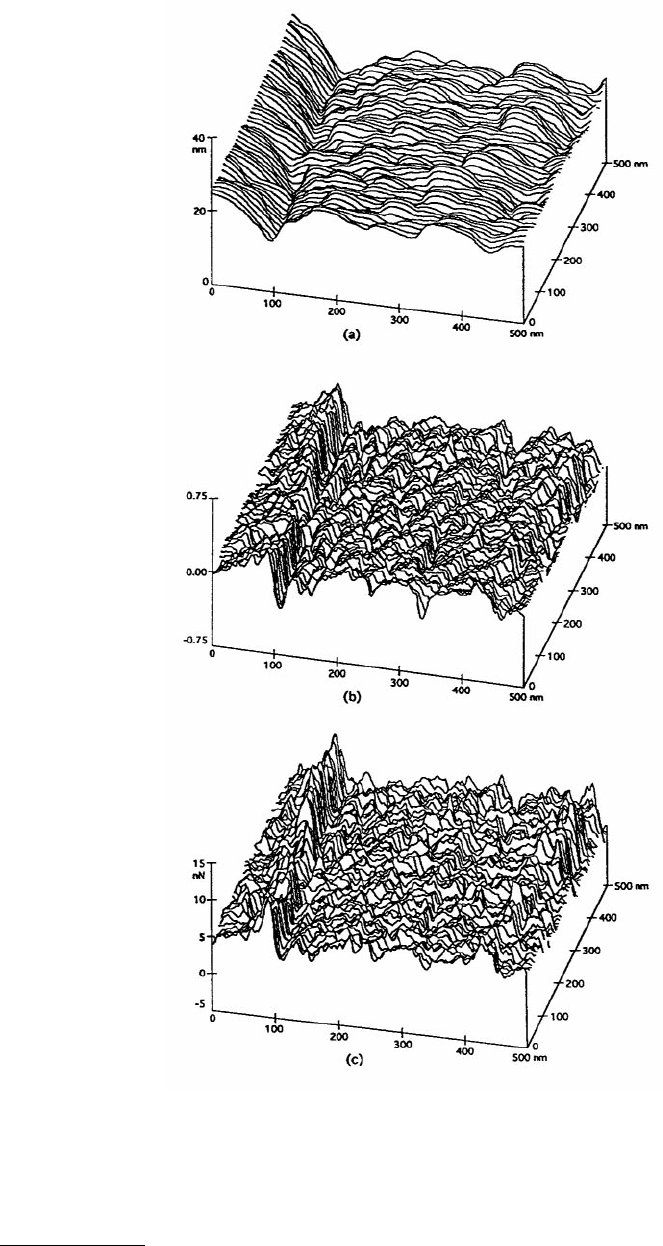
FIGURE 14.12 (a) Surface roughness map (σ = 4.4 nm), (b) slope of the roughness proﬁles taken in the sample

sliding direction (the horizontal axis) (mean = 0.023, σ = 0.197), and (c) friction force map (mean = 6.2 nN, σ =

2.1 nN) for a textured and lubricated thin-ﬁlm rigid disk for a normal load of 160 nN. (From Bhushan, B. and Ruan,

J., 1994, ASME J. Tribol. 116, 389–396. With permission.)

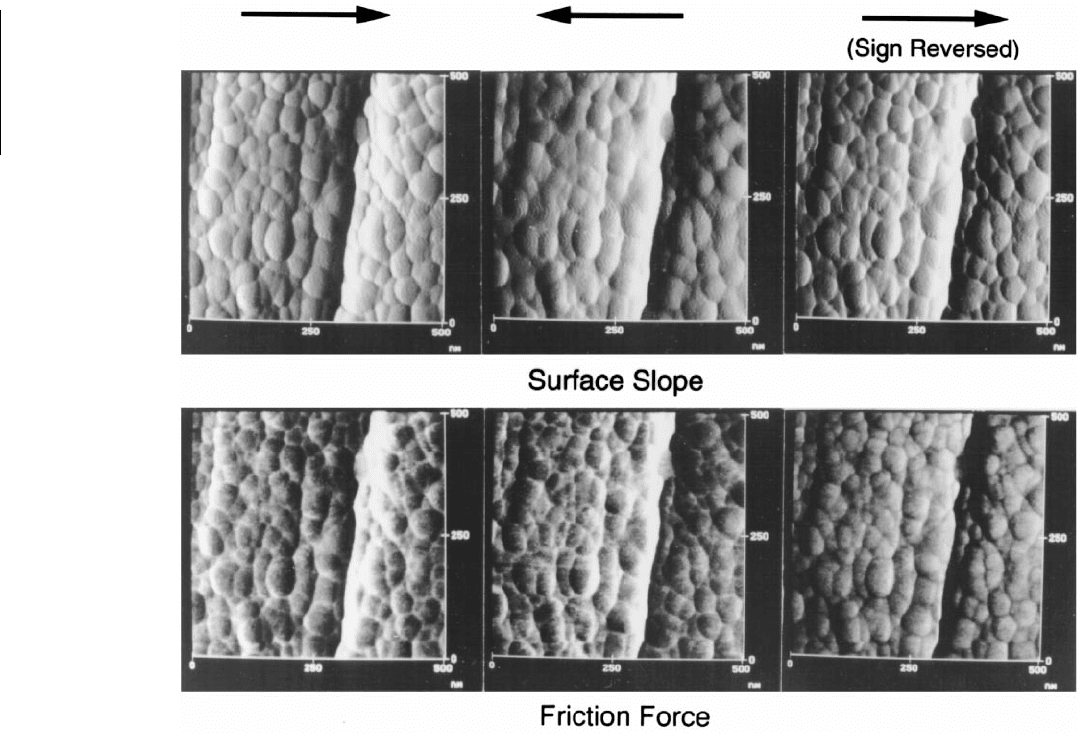
FIGURE 14.13 Gray-scale plots of the slope of the surface roughness and the friction force maps for a textured and lubricated thin-

ﬁlm rigid disk. Arrows indicate the tip sliding direction. Higher points are shown by lighter color.

FIGURE 14.14 (a) Surface roughness map (σ = 7.9 nm), (b) slope of the roughness proﬁles taken along the sample

sliding direction (mean = –0.006, σ = 0.300), and friction force map (mean = 5.5 nN, σ = 2.2 nN) of an MP tape

at a normal load of 70 nN. (From Bhushan, B. and Ruan, J., 1994, ASME J. Tribol. 116, 389–396. With permission.)

FIGURE 14.15 Gray-scale plots of the slope of the roughness and the friction force maps for an MP tape. Arrows indicate the tip sliding

direction. Higher points are shown by lighter color.

FIGURE 14.16 Surface roughness map (σ = 15.4 nm), slope of the roughness map (mean = –0.052, σ = 0.224),

and the friction force map (σ = 2.1 nN) of a polished natural (IIa) diamond crystal. (From Bhushan, B. and Ruan,

J., 1994, ASME J. Tribol. 116, 389–396. With permission.)

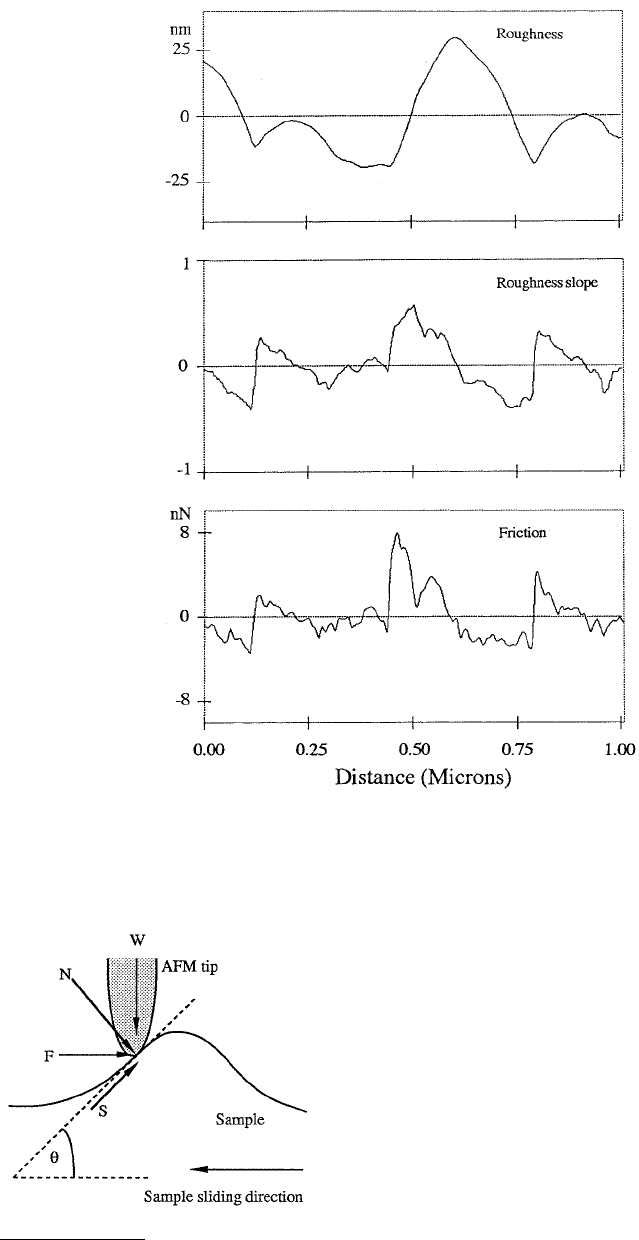
FIGURE 14.17 Schematic illustration showing the effect of an

asperity (making an angle θ with the horizontal plane) on the

surface in contact with the tip on local friction in the presence of

“adhesive” friction mechanism. W and F are the normal and fric-

tion forces, respectively. S and N are the force components along

and perpendicular to the local surface of the sample at the contact

point, respectively.

(14.5)

if µ

tan θ is small. For a symmetrical asperity, the average coefﬁcient of friction experienced by the FFM

tip traveling across the whole asperity is

(14.6)

if µ

tan θ is small.

The plowing component of friction (Bowden and Tabor, 1950) with tip sliding in either direction is

(14.7)

Since in the FFM measurements, we notice little damage of the sample surface, the contribution by

plowing is expected to be small and the ratchet mechanism is believed to be the dominant mechanism

for the local variations in the friction force proﬁle. With the tip sliding over the leading (ascending) edge

of an asperity, the slope is positive; it is negative during sliding over the trailing (descending) edge of the

asperity. Thus, friction is high at the leading edge of asperities and low at the trailing edge. The ratchet

mechanism thus explains the correlation between the slopes of the roughness proﬁles and friction proﬁles

observed in Figures 14.11 to 14.16. We note that in the ratchet mechanism, the FFM tip is assumed to

be small compared to the size of asperities. This is valid since the typical radius of curvature of the tips

is about 30 nm. The radius of curvature of the asperities of the samples measured here (the asperities

that produce most of the friction variation) is found to be typically about 100 to 200 nm, which is larger

than that of the FFM tip (Bhushan and Blackman, 1991).

We also note that the variation in attractive adhesive force (W

att

) with topography can also contribute

to observed variation in friction (Mate, 1993a,b). The total force in the normal direction is the intrinsic

force (W

att

) in addition to the applied normal load (W). Thus, friction force

where µ is the coefﬁcient of friction. Based on Mate (1993a), major components of the attractive adhesive

force are the van der Waals force (between the tip and the summits and valleys of the mating sample

surface) and meniscus or capillary forces. Approximating the tip–sample surface geometry as a sphere

on a ﬂat, the magnitude of the attractive van der Waals force can be expressed as (Derjaguin et al., 1987)

(14.8a)

and

(14.8b)

µ=µ−

()

+µ

()

µ−

20 0

1tan tan

~ tan ,

θθ

µ=µ+µ

()

=µ +

()

−µ

()

µ+

()

ave 1 2

tan tan

~ tan ,

θθ

~ tan .θ

FWW=µ +

()

att

vdW

=π

()

γγ ,

where A is the Hamaker constant, R is the tip radius, D is the separation distance by the surface roughness

of the means of the tip and the sample surfaces, γ

and γ

are the surface energies of the tip and sample

surfaces, and D

~ 0.2 nm (Israelachvili, 1992). As a consequence of the strong 1/D

dependence, the tip

should experience a much weaker van der Waals force on the top of a summit as compared with that of

a valley. Mate (1993a) reported that a separation change ∆D of 5 nm would give a variation in the van

der Waals force by a factor of 5 if the distance of closest approach, approximately the amount of roughness

separation between the two surfaces, is 4 nm. Another component of the attractive adhesive force in the

presence of liquid ﬁlm is the meniscus force. The meniscus force for a sphere on a ﬂat in the presence

of liquid is

(14.9)

where γ

is the surface tension of the liquid. Meniscus force is generally much stronger than the van der

Waals force. Thus, the contribution of adhesion mechanism to the friction force variation is relatively

small for samples used in this study. Furthermore, the correlation between the surface and friction force

proﬁles is poor; therefore, an adhesion mechanism cannot explain the topography effects. The ratchet

mechanism already quantitatively explains the variation of friction.

Since the local friction force is a function of the local slope of sample surface, the local friction force

should be different as the scanning direction of the sample is reversed. Figures 14.13 and 14.15 show the

gray-scale plots of slope of roughness proﬁles and friction force proﬁles for a lubricated textured disk

and an MP tape, respectively. The left side of the ﬁgures corresponds to the tip sliding from the left

toward the right (or the sample sliding from the right to the left). We again note a general correspondence

between the surface roughness slope and the friction proﬁles. The middle ﬁgures in Figures 14.13 and

14.15 correspond to the tip sliding from the right toward left. We note that generally the points that have

high friction force and high slope in the left-to-right scan have low friction and low slope as the sliding

direction is reversed (Meyer and Amer, 1990; Grafstrom et al., 1993; Overney and Meyer, 1993; Bhushan

and Ruan, 1994e; Ruan and Bhushan, 1994b). This results from the slope being of opposite sign as the

direction is reversed, which reverses the sign of friction force contribution by the ratchet mechanism.

This relationship is not true at all locations. The right-side ﬁgures in Figures 14.13 and 14.15 correspond

to the left-hand set with sign reversed. On the right, although the sign of friction force proﬁle is the

reverse of the left-hand proﬁle, some differences in the right two friction force proﬁles are observed

which may result from the asymmetrical asperities and/or asymmetrical transfer of wipe material during

manufacturing of the disk. This directionality in microscale friction force was ﬁrst reported by Bhushan

et al. (1994a,c,e, 1995a–d, 1997a, 1998).

If asperities in a sample surface have a preferential orientation, this directionality effect will be man-

ifested in macroscopic friction data; that is, the coefﬁcient of friction may be different in one sliding

direction from that in the other direction. Such a phenomenon has been observed in rubbing wool ﬁber

against horn. It was found that the coefﬁcient of friction is greatest when the wool ﬁber is rubbed toward

its tip (Mercer, 1945; Lipson and Mercer, 1946; Thomson and Speakman, 1946). Makinson (1948)

explained the directionality in the friction by the “ratchet” effect. Here, the ratchet effect is the result of

large angle θ, where instead of true sliding, rupture or deformation of the ﬁne scales of wool ﬁbers occurs

in one sliding direction. We note that the frictional directionality can also exist in materials with particles

having a preferred orientation.

The directionality effect in friction on a macroscale is also observed in some magnetic tapes. In a

macroscale test, a 12.7-mm-wide MP tape was wrapped over an aluminum drum and slid in a recipro-

cating motion with a normal load of 0.5 N and a sliding speed of about 60 mm/s. The coefﬁcient of

friction as a function of sliding distance in either direction is shown in Figure 14.18. We note that the

coefﬁcient of friction on a macroscale for this tape is different in different directions.

=π4 γ

14.4.2.3 Silicon

Coefﬁcient of microscale friction data for virgin, treated, and coated Si(111) samples are presented in

Table 14.5 (Bhushan et al., 1994a). (Also see Bhushan et al., 1993c, 1997a,b; Sundararajan and Bhushan,

1998.) We note that crystalline orientation of silicon has little effect on the coefﬁcient of friction. PECVD

oxide-coated Si(111) exhibits a coefﬁcient of friction value lower than that of any other silicon sample.

14.5 Scratching and Wear

14.5.1 Nanoscale Wear

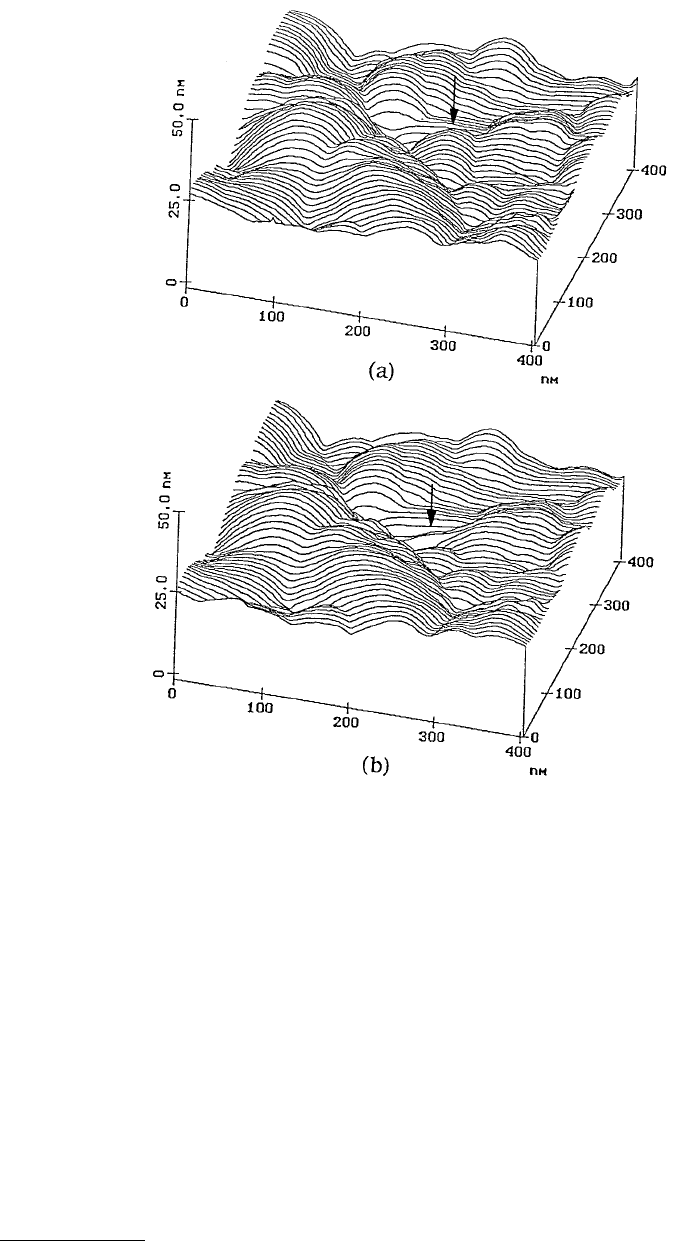
Bhushan and Ruan (1994e) conducted nanoscale wear tests on MP tapes at a normal load of 100 nN.

Figure 14.19 shows the topography of the MP tape obtained at two different loads. For a given normal

load, measurements were made twice. There was no discernible difference between consecutive measure-

ments for a given normal load. However, as the load increased from 10 to 100 nN, topographical changes

were observed; material (indicated by an arrow) was pushed toward the right side in the sliding direction

of the AFM tip relative to the sample. The material movement is believed to occur as a result of plastic

deformation of the tape surface. Similar behavior was observed on all tapes. Magnetic tape coating is

made of magnetic particles and polymeric binder. Any movement of the coating material can eventually

lead to loose debris. Debris formation is an undesirable situation as it may contaminate the head, which

may increase friction and/or wear between the head and tape, in addition to the deterioration of the tape

itself. With disks, they did not notice any deformation under a 100 nN normal load.

FIGURE 14.18 Coefﬁcient of macroscale friction as a function

of sliding cycles for an MP tape sliding over an aluminum drum

in a reciprocating mode in both directions. Normal load = 0.5 N

over 12.7-mm-wide tape, sliding speed = 60 mm/s.

TABLE 14.5 Roughness (σ), Microfriction, Microscratching/Microwear, and Nanoindentation Hardness Data

for Various Virgin, Coated, and Treated Silicon Samples

Material

σ (nm)

500 × 500 nm

Coefﬁcient

of Friction

Scratch Depth at

40 µN

(nm)

Wear Depth at

40 µN

(nm)

Hardness at

100 µN

(GPa)

Si(111) 0.11 0.03 20 27 11.7

Si(110) 0.09 0.04 20 — —

Si(100) 0.12 0.03 25 — —

Polysilicon 1.07 0.04 18 — —

Polysilicon (lapped) 0.16 0.05 18 25 12.5

PECVD oxide-coated Si(111) 1.50 0.01 8 5 18.0

Dry-oxidized Si(111) 0.11 0.04 16 14 17.0

Wet-oxidized Si(111) 0.25 0.04 17 18 14.4

-implanted Si(111) 0.33 0.02 20 23 18.6

Scan area.

From Bhushan, B. and Koinkar, V.N., 1994, J. Appl. Phys. 75, 5741–5746. With permission.

14.5.2 Microscale Scratching

Microscratches have been made on various potential head slider materials (Al

, Al

–TiC, Mn–Zn

ferrite, and SiC), various magnetic media (unlubricated polished thin-ﬁlm disk, MP, BaFe, ME tapes,

PET substrates) and virgin, treated, and coated Si(111) wafers at various loads (Miyamoto et al., 1991c,

1993; Bhushan et al., 1994a,c,d, 1995a–e, 1997a, 1998; Koinkar and Bhushan, 1996a, 1997b; Sundararajan

and Bhushan, 1998). As mentioned earlier, the scratches are made using a diamond tip.

14.5.2.1 Head Slider Materials

Scratch depths as a function of load and representative scratch proﬁles with corresponding two-dimen-

sional gray scale plots at various loads after a single pass (unidirectional scratching) for Al

, Al

–TiC,

polycrystalline and single-crystal Mn–Zn ferrite and SiC are shown in Figures 14.20 and 14.21, respec-

tively. Variation in the scratch depth along the scratch is about ±15%. The Al

surface could be scratched

FIGURE 14.19 Surface roughness maps of an MP tape at applied normal load of (a) 10 nN and (b) 100 nN. Location

of the change in surface topography as a result of nanowear is indicated by arrows. (From Bhushan, B. and Ruan,

J., 1994, ASME J. Tribol. 116, 389–396. With permission.)

at a normal load of 40 µN. The surface topography of polycrystalline Al

shows the presence of porous

holes on the surface. The two-dimensional gray scale plot of the scratched Al

surface shows one porous

hole between scratches made at normal loads of 40 and 60 µN. Regions with defects or porous holes

present, exhibit lower scratch resistance (see region marked by the arrow on two-dimensional gray-scale

plot of Al

). The Al

–TiC surface could be scratched at a normal load of 20 µN. The scratch resistance

for TiC grains is higher than that of Al

grains. The scratches generated at normal loads of 80 and

100 µN show that the scratch depth of Al

grains is higher than that of TiC grains (see corresponding

gray-scale plot for Al

–TiC). Polycrystalline and single-crystal Mn–Zn ferrite could be scratched at a

normal load of 20 µN. The scratch width is much larger for the ferrite specimens as compared with other

specimens. For SiC there is no measurable scratch observed at a normal load of 20 µN. At higher normal

loads very shallow scratches are produced. Table 14.2 presents average scratch depth at 60 µN normal

load for all specimens. SiC has the highest scratch resistance followed by Al

–TiC, Al

, and poly-

crystalline and single-crystal Mn–Zn ferrite. Polycrystalline and single-crystal Mn–Zn ferrite specimens

exhibit comparable scratch resistance.

14.5.2.2 Magnetic Media

Scratch depths as a function of load and scratch proﬁles at various loads after ten scratch cycles for

unlubricated, polished disk, and MP tape are shown in Figures 14.22 and 14.23, respectively. We note

that scratch depth increases with an increase in the normal load. Tape could be scratched at about 100 nN.

With disk, gentle scratch marks under 10 µN load were barely visible. It is possible that material removal

did occur at lower load on an atomic scale which was not observable with a scan size of 5 µm square.

For disk, scratch depth at 40 µN is less than 10 nm deep. The scratch depth increased slightly at the load

of 50 µN. Once the load is increased in excess of 60 µN, the scratch depth increased rapidly. Bhushan

et al. (1994c) believed that the DLC coating cracked at about 60 µN. These data suggest that the carbon

coating on the disk surface is much harder to scratch than the underlying thin-ﬁlm magnetic ﬁlm. This

is expected since the carbon coating is harder than the magnetic material used in the construction of the

disks.

Since tapes scratch readily, for comparisons in scratch resistance of various tapes, Bhushan et al. (1995c)

made scratches on three tapes with one cycle. Figure 14.24 presents the scratch depths as a function of

normal load after one cycle for three tapes — MP, BaFe, and ME tapes. For the MP and BaFe particulate

tapes, Bhushan et al. (1995c) noted that the scratch depth along (parallel) and across (perpendicular)

FIGURE 14.20 Scratch depth as a function of normal load after one unidirectional cycle for Al

, Al

–TiC,

polycrystalline Mn–Zn ferrite, single-crystal Mn–Zn ferrite, and SiC. (From Koinkar, V.N. and Bhushan, B., 1996,

Wear 202, 110–122. With permission.)