Birge J.R., Louveaux F. Introduction to Stochastic Programming

Подождите немного. Документ загружается.

174 4 The Value of Information and the Stochastic Solution

=(1 −p

)



∗

+ p

∗

(

∑

k=r

∗

(

)



=(1 −p

)



∗

∑

k=1

∗

(

)



=(1 −p

)RP ,

which proves the desired inequality.

To obtain upper bounds on RP that relate to the pairs subproblem, we general-

ize the VSS deﬁnition. Let z(x,

) be the deterministic problem associated with

scenario

(remember

need not necessarily be a possible scenario) and ¯x

optimal solution to min

z(x,

) . We may then deﬁne the expected value of the

reference scenario,

EVRS = E

z( ¯x

,ξ) ,

and the value of a stochastic solution to be

VSS = EVRS−RP .

Note that VSS is still nonnegative, because ¯x

is either a feasible solution to the

recourse problem and EVRS ≥ RP or an infeasible solution so that EVRS =+∞ .

Now, as before, let (¯x

, ¯y

,y(

)) be optimal solutions to the pairs subproblem

and

, k = 1,...,K . Deﬁne the expectations of pairs expected value to be

EPEV = min

k=1,...,K∪{r}

z( ¯x

,ξ) .

Proposition 8. RP ≤EPEV ≤ EVRS .

Proof: The three values are the optimal value of the recourse function min

z(x,ξ) over smaller and smaller feasibility sets: the ﬁrst one over all feasible

x in K

∩K

, the second one over x ∈K

∩K

∩{¯x

, k = 1,...,K ∪{r}},andthe

third one over ¯x

∩K

Putting these two propositions together, one obtains the following theorem.

Theorem 9. 0 ≤EVRS−EPEV ≤ VSS ≤ EVRS−SPEV ≤ EVRS −WS .

We apply these concepts in the following example.

Example 2

Consider the problem to ﬁnd:

min 3x

+ 2x

+ E

min(−15y

−12y

)

4.6 Bounds on EVPI and VSS 175

s. t. 3y

+ 2y

≤ x

+ 5y

≤ x

.8ξ

≤ y

≤ ξ

.8ξ

≤ y

≤ ξ

x,y ≥0 ,

where ξ

= 4or6andξ

= 4 or 8 , independently of each other, with probability

1/2 each.

This example can be seen as an investment decision in two resources x

and x

which are needed in the second-stage problem to cover at least 80% of the demand.

In this situation, the EEV and WS answers are totally inconclusive.

Table 1 gives the various solutions under the four scenarios, the optimal objective

values under these scenarios and the WS value. It also describes the EV value

under the expected value scenario

=(5,6)

. Note that this scenario is not one

of those possible. The optimal solution ¯x(

)=(24.6,34)

is infeasible for the

stochastic problem so that EEV is set to be +∞ .

Table 1 Solutions and optimal values under the four scenarios and the expected value scenario.

Scenario First-Stage Second-Stage Optimal Value

Solution Solution z(¯x(

)

1. (4,4) (18.4, 24) (4, 3.2) 4.8

2. (6,4) (24.4, 28) (6, 3.2) 0.8

3. (4,8) (24.8, 40) (4, 6.4) 17.6

4. (6,8) (30.8, 44) (6, 6.4) 13.6

WS = 9.2

=(5,6) (24.6, 34) (5, 4.8) EV = 9.2

EEV =+∞

It follows from Table 1 that EV = WS = 9.2 ≤ RP ≤ EEV =+∞ . This rela-

tion is of no help: we can only conclude from it that EVPI is somewhere between

0and+∞ ,andsois VSS . These statements could have been made without any

computation.

It is in such situations that the pairs subproblems are of great interest. Because

the problem under consideration is an investment problem with demand satisfaction

constraints, the most logical reference scenario corresponds to the largest demand,

=(6,8)

, and not to the mean demand

This will force the ﬁrst-stage decisions to take demand satisfaction under the

maximal demand into consideration, so that decisions taken under the pairs sub-

problem are feasible for the recourse problem. Due to independence,

is one of

the possible realizations of

, with p

= 1/4.

176 4 The Value of Information and the Stochastic Solution

The pairs subproblems of

and

are

min 3x

+ 2x

−

(15y

+ 12y

) −

(15y

+ 12y

)

s. t. x

≥ 27.2 , 3y

+ 2y

≤ x

, 3y

+ 2y

≤ x

≥ 41.6 , 2y

+ 5y

≤ x

, 2y

+ 5y

≤ x

4.8 ≤ y

≤ 6 ,.8

≤ y

≤

6.4 ≤ y

≤ 8 ,.8

≤ y

≤

y ≥ 0 .

The bounds on x

and x

are induced by the feasibility for the reference scenarios.

Table 2 gives the solutions of the pairs subproblems for the three scenarios (other

than the reference scenario), the SPEV ,the EVRS ,andthe EPEV values.

Table 2 Pairs subproblems solutions.

Pairs First-Stage Second-Stage Second-Stage Objective

Subproblem Solution under under Va lue z

Reference Sc.

1. (4,4), r (27.2, 41.6) (4.8, 6.4) (4,4) 46.6

2. (6,4), r (27.2, 41.6) (4.8, 6.4) (6,4) 24.1

3. (4,8), r (27.2, 41.6) (4.8, 6.4) (4, 6.72) 22.12

SPEV = 30.94

EPEV = min

z(¯x(ξ

),ξ)=E

z(27.2,41.6,ξ)

= 30.94

EVRS = E

z((30.8,44),

)=40.6

This time, the relations one can derive from this table are strongly

conclusive:

WS = 9.2 ≤SPEV = 30.94 ≤ RP ≤EPEV = 30.94 ≤ EVRS = 40.6

implies RP = 30.94 and (27.2,41.6)

is an optimal solution.

Exercises

1. Show that Proposition 1 still holds if some of the x and/or y must be integer.

2. Consider Example 3.5 (with recourse function given in (3.3.1)) with a single

ﬁrst-stage decision x with ﬁrst-stage cost c ·x and

Q(x,ξ)=min{2y

+ y

| y

≥ x −ξ, y

≥ ξ −x,y ≥0, integer }

4.6 Bounds on EVPI and VSS 177

with ξ = 1 or 2 with probability of 1/2 each. Show:

(a) If x must be integer, then EV > WS for any value of c ≥0.

(b) If x is continuous, then EV = WS for 0 ≤c ≤1andEV > WS for c > 1.

Beware that y is always integer; the discussion here concerns the effect of

x ’s being integer or not.

3. Consider the following stochastic program

min

x≥0

2x + E

{ξ ·y |y ≥ 1 −x, y ≥0} ,

and ξ takes on values 1 and 3 with probability 3/4and1/ 4 , respectively.

Show that in this case EV > WS .

4. Consider the following two-stage program:

min 2x

+ x

+ E

(−3y

−4y

+ 2y

≥ ξ

≤ x

≤ ξ

,y ≥ 0)

s. t. x

+ x

≤ 7 , x

≥ 0 ,

where ξ can take the values













with probability 1/3 each.

(a) Choose the scenario





as the reference scenario. Deﬁne the problem

z(x,ξ) for this reference scenario. Its optimal solution gives the optimal

ﬁrst-stage decision x

= 4, x

= 3 . Compute the EVRS value.

(b) State the pairs subproblem for





and the reference scenario.





and the reference scenario

has ﬁrst-stage optimal solutions x

= 5, x

= 2 ; the solution of the pairs

subproblem for





and the reference scenario has ﬁrst-stage optimal so-

lutions x

= 4, x

= 3 . Compute the values of the two pairs subproblems.

Compute the SPEV value. What relation holds for the recourse problem

value?

5. Adapt the proofs in Proposition 7 for the case where r ∈

6. Prove that the bounds in this chapter remain valid under general constraints

x ∈ X and y ∈ Y (x) that may, for example, involve integrality restrictions.

(Sandikc¸i, Kong, and Schaefer [2009]).

7. Fill in the corresponding entries for Tables 1 and 2 with the added restriction

that all decision variables must be integers.

Part III

Solution Methods

Chapter 5

Two-Stage Recourse Problems

Computation in stochastic programs with recourse has focused on two-stage prob-

lems with ﬁnite numbers of realizations. This problem was introduced in the farming

example of Chapter 1. As we saw in the capacity expansion model, this problem can

also represent multiple stages of decisions with block separable recourse and it pro-

vides a foundation for multistage methods. The two-stage problem is, therefore, our

primary model for computation.

The general model is to choose some initial decision that minimizes current costs

plus the expected value of future recourse actions. With a ﬁnite number of second-

stage realizations and all linear functions, we can always form the full deterministic

equivalent linear program or extensive form. With many realizations, this form of the

problem becomes quite large. Methods that ignore the special structure of stochastic

linear programs become quite inefﬁcient (as some of the results in Section 5.1d.

show). Taking advantage of structure is especially beneﬁcial in stochastic programs

and is the focus of much of the algorithmic work in this area.

The method used most frequently is based on building an outer linearization of

the recourse cost function and a solution of the ﬁrst-stage problem plus this lin-

earization. This cutting plane technique is called the L -shaped method in stochastic

programming. Section 5.1 describes the basic L -shaped method and describes the

cut construction in some detail. Section 5.1c. gives a formal proof of convergence

of the L -shaped method while the following subsections continue this development

with a discussion of enhancements of the L -shaped method in terms of multicuts

and bunching of realizations. Variants adding nonlinear regularized terms are stud-

ied in Section 5.2 and with quadratic objectives in Section 5.3. Other extensions

of the L-shaped method include its use with bounding techniques, which will be

considered in Chapter 8, and in combination with sampling methods, which will be

studied in Chapter 9.

The remainder of this chapter discusses alternative algorithms. In Section 5.6,

we describe alternative decomposition procedures. The ﬁrst method is an inner lin-

earization, or Dantzig-Wolfe decomposition approach, that solves the dual of the

L -shaped method problem. The other approach is a primal form of inner lineariza-

tion based on generalized programming. Section 5.5 considers direct approaches

J.R. Birge and F. Louveaux, Introduction to Stochastic Programming, Springer Series 181

in Operations Research and Financial Engineering, DOI 10.1007/978-1-4614-0237-4

 Springer Science+Business Media, LLC 2011

182 5 Two-Stage Recourse Problems

to the extensive form through efﬁcient extreme point and interior point methods.

We discuss basis factorization and its relationship to decomposition methods. We

also present interior point approaches and the use of a special stochastic program-

ming structure for these algorithms. Methods based on nonlinear optimization of

the Lagrangian appear in Section 5.8. Section 5.9 discusses additional methods and

considerations of computational complexity.

5.1 The L -Shaped Method

Consider the general formulation in (3.1.2)or(3.1.5). The basic idea of the L -

shaped method is to approximate the nonlinear term in the objective of these prob-

lems. A general principle behind this approach is that, because the nonlinear ob-

jective term (the recourse function) involves a solution of all second-stage recourse

linear programs, we want to avoid numerous function evaluations for it. We there-

fore use that term to build a master problem in x , but we only evaluate the recourse

function exactly as a subproblem.

To make this approach possible, we assume that the random vector ξ has ﬁ-

nite support. Let k = 1,...,K index its possible realizations and let p

be their

probabilities. Under this assumption, we may now write the deterministic equiva-

lent program in the extensive form. This form is created by associating one set of

second-stage decisions, say, y

, to each realization ξ , i.e., to each realization of

, h

,and T

. It is a large-scale linear problem that we can deﬁne as the extensive

form ( EF ):

(EF) min c

x +

∑

k=1

s. t. Ax = b ,

x + Wy

= h

, k = 1,...,K ;

x ≥ 0 , y

≥ 0 , k = 1,...,K .

(1.1)

An example of an extensive form has been given for the farmer’s problem in

Chapter 1 (Model (1.1.2)).

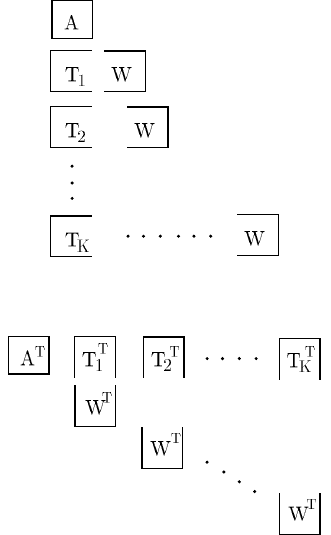
The block structure of the extensive form appears in Figure 1. This picture has

given rise to the name, L -shaped method for the following algorithm. Taking the

dual of the extensive form, one obtains a dual block-angular structure, as in Figure 2.

Therefore it seems natural to exploit this dual structure by performing a Dantzig-

Wolfe [1960] decomposition (inner linearization) of the dual or a Benders [1962]

decomposition (outer linearization) of the primal. This method has been extended

in stochastic programming to take care of feasibility questions and is known as Van

Slyke and Wets’s [1969] L -shaped method. It proceeds as follows.

5.1 The L -Shaped Method 183

Fig. 1 Block structure of the two-stage extensive form.

Fig. 2 Block angular structure of the two-stage dual.

L -Shaped Algorithm

Step 0.Set r = s =

= 0.

Step 1.Set

+ 1 . Solve the linear program (1.2)–(1.4)

min z = c

x +

(1.2)

s. t. Ax = b ,



x ≥d



,= 1,...,r , (1.3)



x +

≥ e



,= 1,...,s , (1.4)

x ≥0 ,

∈ ℜ .

Let (x

) be an optimal solution. If no constraint (1.4)ispresent,

is set equal

to −∞ and is not considered in the computation of x

Step 2. Check if x ∈ K

If not, add at least one cut (1.3) and return to Step 1.

Otherwise, go to Step 3.