Благовещенский С.Н., Холодилин А.Н. Справочник по статике и динамике корабля. Динамика корабля. Том 2

Подождите немного. Документ загружается.

Распределение Релея, строго говоря, применимо только для узких спектров

при

е -^ 0,4. Для широких спектров высота волны может быть определена по фор-

муле

А. Г. Степанова

(1.3)

К, = V2n (1 — е

Для узких спектров эта формула переходит в известную формулу

hw = 2,50

На

рис. 1.6 приведены графики взаимной зависимости основных параметров

волны: длины, крутизны,

угла

волнового склона. На рисунке обозначено: / —

К, =

0.17*

;

2-К=*

0.22Я,

715

Для периодов не получены законы распределения, устанавливающие связи

между

статистическими характеристиками периодов и спектральными характери-

стиками процесса.

Эмпирический

закон распределения „

периодов, предложенный Ю. М. Крыловым,

»Д

выражается зависимостью \_ . »•

0,05

0№

0,02

0,01

121,0

0,8 0,7

0,5

а'

Рис.

1.6

где т — период, определенный с учетом "

вторичных экстремумов; х — средний пе-

риод; Г — гамма-функции (Приложе-

ние

2).

Используя гипотезу о том, что периоды волн не связаны статистически с их

высотами, двухмерный закон распределения высот и периодов представляют в виде

произведения соответствующих одномерных функций

Здесь высоты волны определены с учетом вторичных экстремумов.

§ 3. СПЕКТРЫ ВОЛНЕНИЯ

Реальное трехмерное нерегулярное волнение может быть описано с помощью

двухмерной спектральной плотновти Sj (а, %), где % —

угол

между

главным на-

правлением распространения волн (обычно направлением ветра) и направлением,

котором определяется двухмерный спектр. Однако такое представление спектра

неудобно для практических расчетов. Предполагая, что двухмерное волнение заклю-

чает в себе всю энергию волнового движения, которое при наличии трехмерных

волн распространяется в различных направлениях, можно установить энергетиче-

ское соотношение

между

спектрами двухмерного и трехмерного волнений, т. е.

между

двухмерным и одномерным спектрами. При этом учитывается, что спектральные

составляющие трехмерного волнения имеют наибольшую энергию в пределах ±30°

от направления ветра, хотя бывают случаи, когда волны приходят и под большим

углом.

В настоящее время наибольшей популярностью пользуется формула

Артура

•

Sj (a)

cos*

(1.5)

где

—я/2 < х < я/2.

Формула

Артура

позволяет перейти от двухмерного спектра к одномерному.

Эта формула рекомендована и 12-й Международной конференцией опытовых бас-

сейнов

(МКОБ),

РИМ, 1969 г в качестве стандартной

При

решении большинства инженерных задач качки пользуются одномерным

-спектром Принципиально возможно получить спектр двумя путями.

Аппроксимировать корреляционную функцию волновых ординат, например,

выражением

К(т)~Р

cos6

где а = 0,21 Р — коэффициент, характеризующий степень нерегулярности волне-

ния;

Р = 0,82 а

, где а

— частота, соответствующая максимуму спектра, т —

интервал времени.

Таким

лутем

получен спектр Рахманина—Фирсова

J^±i!)

(°

(16)

Ч«

2а») а* + 2а* (а* - р) + (о» + Р

)

Особенностью этого спектра является заметное перераспределение энергии

волнения

из области высоких частот в диапазон низких частот. Кроме того, Sg (a)

не

равно нулю при a = 0.

2. Задаться спектром Барлинга

(О) = Дог-* ехр (—Во-"), (1.7)

где Л, В, k, n — параметры, зависящие от условия волнообразования.

Параметры, применяемые при расчетах спектров волнения, отличаются только

значениями

(табл. 1 3).

Двенадцатая Международная конференция опытовых бассейнов рекомендует

пользоваться типовыми спектрами волнения для тех районов моря и условий, для

которых они получены, а при отсутствии

(

такой информации—временным стандар-

том спектра

(1.8)

Где h-щ — значительная высота волны, см; g — ускорение силы тяжести, g —

«= 981 см-с"

; Sj (or) — см* с.

Этот спектр может быть применен для приближенной оценки развивающегося

угасающего волнений В этом

случае

/ D i

(1.9)

"i/з /

где

Здесь К — коэффициент степени развитости волнения. Для полностью развитого

волнения

К = 1, К < 1

соответствует

развивающемуся волнению; К> 1 —мертвой

зыби

В первом приближении можно положить ^щ/Ajл = З9,3/С

, где }»

—•

длине

волны,

соответствующая максимуму спектра.

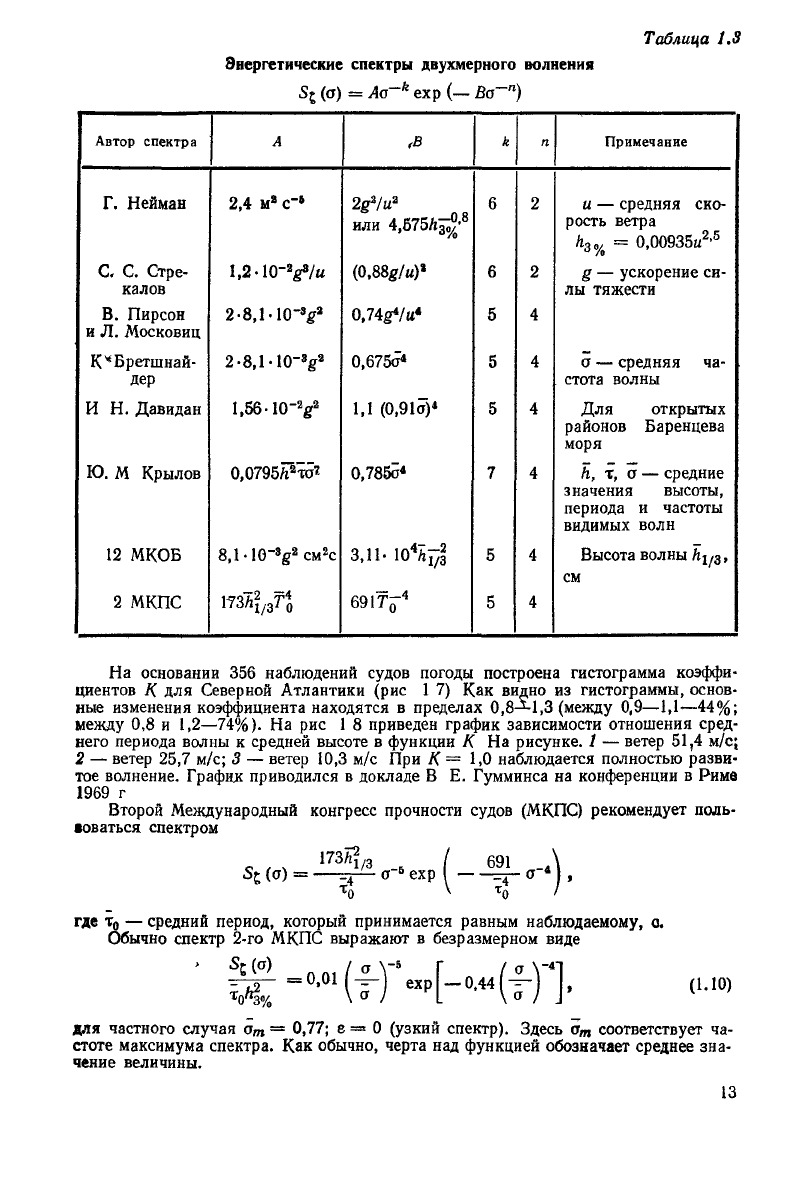
Таблица 1.3

Энергетические спектры двухмерного волнения

Sj (a) = Aa~

ехр (— Ва~

)

Автор спектра

Г. Нейман

С. С. Стре-

калов

В. Пирсон

Л. Московиц

К*Бретшнай-

дер

Н. Давидан

Ю. М Крылов

12 МКОБ

МКПС

2,4 м» с"»

l,2-10-V/«

2-8,1-10-»g*

2-8,1-10-V

1,56-lO'V

0,0795А*та*

8.M0Y

см

173Л

1/3

2^/«

или

4,675Л^-

(0№g/u)*

0,74gV««

0,675а*

1,1 (0,91а)*

0,785а*

3,11- I0

A^§

691ГЗ"

Примечание

u — средняя ско-

рость ветра

0,00935и

g — ускорение си-

лы тяжести

а — средняя ча-

стота волны

Для открытых

районов Баренцева

моря

К, т, а — средние

значения

высоты,

периода и частоты

видимых волн

Высота волны Лу

см

На

основании 356 наблюдений

судов

погоды построена гистограмма

коэффи-

циентов К для Северной Атлантики (рис 1 7) Как видно из гистограммы, основ-

ные изменения коэффициента находятся в пределах

0,8-^-1,3

(между

0,9—1,1—44%;

между

0,8 и

1,2—74%).

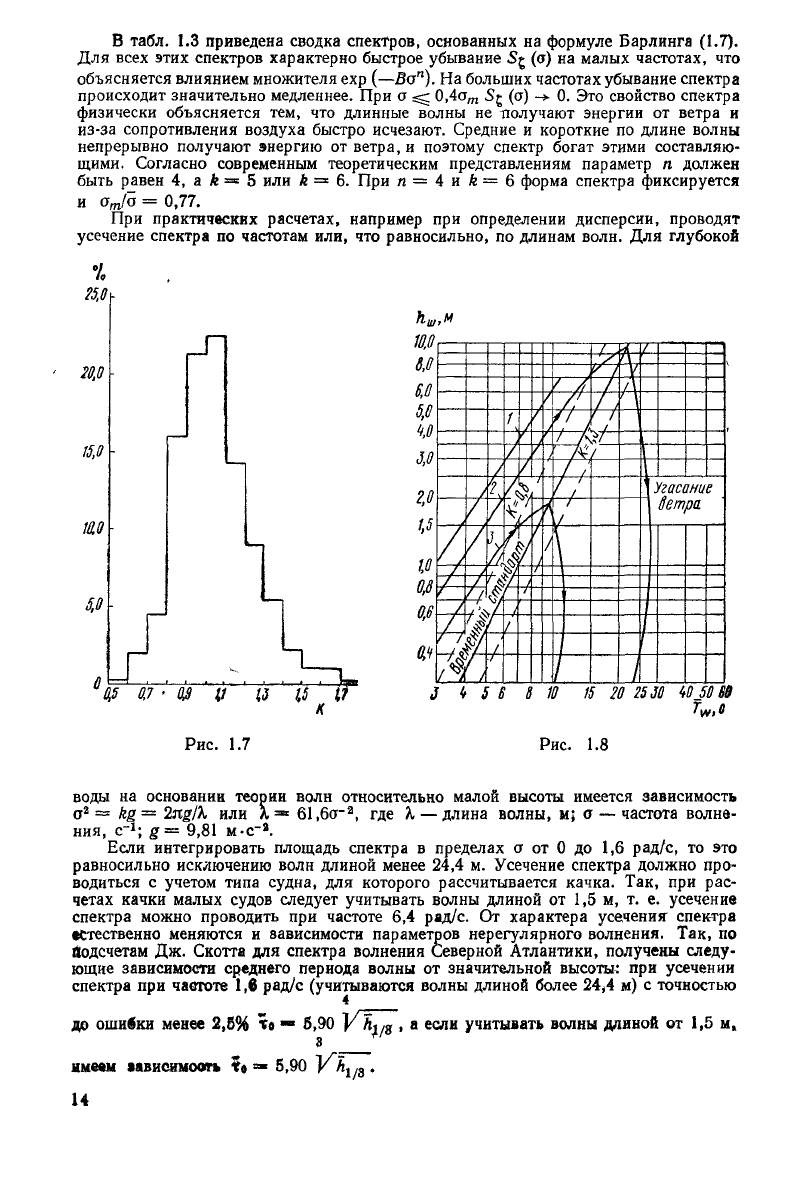
На рис 1 8 приведен график зависимости отношения сред-

него периода волны к средней высоте в функции К На рисунке. 1 — ветер 51,4

M/CJ

— ветер 25,7 м/с; 3 — ветер 10,3 м/с При К — 1,0 наблюдается полностью разви-

тое волнение. График приводился в докладе В Е. Гумминса на конференции в Риме

1969 г

Второй Международный конгресс прочности

судов

(МКПС) рекомендует поль-

зоваться спектром

173ft?

691

•ехр

- -=,-

где т

— средний период, который принимается равным наблюдаемому, о.

Обычно спектр 2-го

МКПС

выражают в безразмерном виде

Г (

(МО)

для частного случая а

= 0,77; 8=0 (узкий спектр). Здесь д

соответствует ча-

стоте максимума спектра. Как обычно, черта над функцией обозначает среднее зна-

чение величины.

В табл.

1.3

приведена сводка спектров, основанных

на

формуле Барлинга (1.7).

Для

всех

этих спектров характерно быстрое убывание

Sj (а) на

малых

частотах,

что

объясняется влиянием множителя

ехр

(—Во").

На

больших

частотах

убывание спектра

происходит значительно медленнее.

При а ^с

0,4ст

Sj (a)

-»•

0. Это

свойство спектра

физически

объясняется

тем, что

длинные волны

не

получают энергии

от

ветра

из-за

сопротивления

воздуха

быстро исчезают. Средние

короткие

по

длине волны

непрерывно получают энергию

от

ветра,

поэтому спектр

богат

этими составляю-

щими.

Согласно современным теоретическим представлениям параметр

должен

быть равен

4, a k = 5 или k = 6. При л = 4 и k = 6

форма спектра фиксируется

aja = 0,77.

При

практических

расчетах,

например

при

определении дисперсии, проводят

усечение спектра

по

частотам

или, что

равносильно,

по

длинам волн.

Для

глубокой

що

3,0

6,0

5,0

J,0

2,0

1,5

Ofi

0,6

it 5 В S 10 15 20 2510

Рис.

1.8

АУ

-J4/

Чгасани

Петра.

0,5

0,7

Рис.

1.7

воды

на

основании теории волн относительно малой высоты имеется зависимость

= kg= 1щ1% или

Л.

61,6а-

где

—

длина волны,

щ а —

частота волне-

ния,

с"

; g= 9,81

м-с"

Если интегрировать площадь спектра

пределах

а от 0 до 1,6

рад/с,

то это

равносильно исключению волн длиной менее

24,4 м.

Усечение спектра должно

про-

водиться

учетом

типа судна,

для

которого рассчитывается качка.

Так, при рас-

четах

качки малых

судов

следует

учитывать волны длиной

от 1,5 м, т. е.

усечение

спектра можно проводить

при

частоте

6,4

рад/с.

От

характера усечения спектра

естественно меняются

зависимости параметров нерегулярного волнения.

Так, по

Подсчетам

Дж.

Скотта

для

спектра волнения Северной Атлантики, получены

следу-

ющие зависимости среднего периода волны

от

значительной высоты:

при

усечении

спектра

при

чаетоте

1,6

рад/с (учитываются волны длиной более

24,4 м) с

точностью

до ошибки менее

2,5%

"Со

-» 5,90 Vftug, а

если учитывать волны длиной

от 1,5 м,

имеем аависимооть Те

5,90 Vh,

ч/з

•

При

сравнении

различных

спектров

удобно

их

нормировать.

А. И.

Вознесен-

ский

и Ю. А.

Нецветаев

предложили

нормированный

энергетический

спектр

морского

волнения

представлять

виде

где а — средняя частота, £>£ — дисперсия, k и я — показатели степени, ы'= а/а

здесь а

— частота, соответствующая максимуму спектра.

Нормированный

спектр в общем виде получается при замене действительной

частоты спектра безразмерной величиной и

= о/а

, где в качестве характерной

частоты спектра а

можно принять одно из следующих

трех

значений:

частоту а

, соответствующую максимуму кривой спектра и определяемую из

условия

dStW -p.

da '

среднюю частоту спектра (абсцисса центра тяжести кривой Sj (a)

[ aS

(а) da

ср

—

;

(а)

частоту, отвечающую среднему периоду волны и условно называемую средней

частотой волнения,

o*St

(a) da

(o) da

Тогда истинный спектр выражается через нормированный

Представим в нормированном виде некоторые спектры.

Спектр Г. Неймана (k = 6, п = 2)

при

/а =

0,707;

a/mo

= 1,65, где F

— безразмерная максимальная

ордината спектра.

Спектр К. Бретшнайдера (k = 5, я = 4)

при

/а =

0,712;

= 2,04.

Спектр Рахманина—Фирсова

-0,284

Г(-2-Л'-1,91(-!1-У+1,091 "* 5

«о

l,02a

;

= 1,58.

Для более полного

учета

волнения в широком диапазоне частот возможно пред-

ставить волнение с помощью

двух

спектров, один из которых определяет волнение

зоне максимума и высокочастотной зоне Sr

(а), а второй Sr. (a) — в зоне низких

частот. Тогда общий спектр определится как сумма спектров

(a) = S

(а) + S'

(а).

Во Временном стандарте рекомендуются следующие формулы для составляющих

спектров:

размерность спектров м*>с, дисперсия волновых ординат

= D

= 0,143

(0,5А

)

*; а

{

= 2я/т;

т=

0,77«

;

, = 2я/т

— частота, соответствующая максимуму спектра; о, =•

1.74

(А

«/

! «02=

0-13m

;

0,70о

т1

;

= О.^.

Для представления спектральной плотности

углов

волнового склона

следует

воспользоваться формулами теории волн малой амплитуды ао = kr

; kg = сг

Поскольку спектральная плотность пропорциональна квадрату полувысоты волны,

то спектральную плотность

углов

волнового склона рассчитывают по формуле

Эта формула применяется при расчете бортовой качки судна.

Практическое вычисление спектров. Все спектры типа спектра Барлинга

(см.

табл. 1.3) имеют коэффициенты А, В и ехр (—Ва~

Порядок

расчета.

Вычисляют коэффициенты А, В и выбирают показатели k и я в зависимости

от используемой формульь-

2. Если задана не высота, а балльность волнения, то предварительно выбирают

высоту волны, исходя из заданной балльности волнения как наибольшую из диапа-

зона

волн шкалы волнения. Таблица пересчета волн приведена в табл. 1.4.

Таблица

1.4

Пересчет высот волны

Балл

волнения

Высота волны (верхний предел балла), м

0,25

0,78

1,25

2,00

3,50

6,00

8,50 ,

11,00

0,12

0,36

0,59

0,94

1,66

2,84

4,02

5,20

%з

0,19

0,57

0,95

1,52

2,65

4,55

6.44

8,33

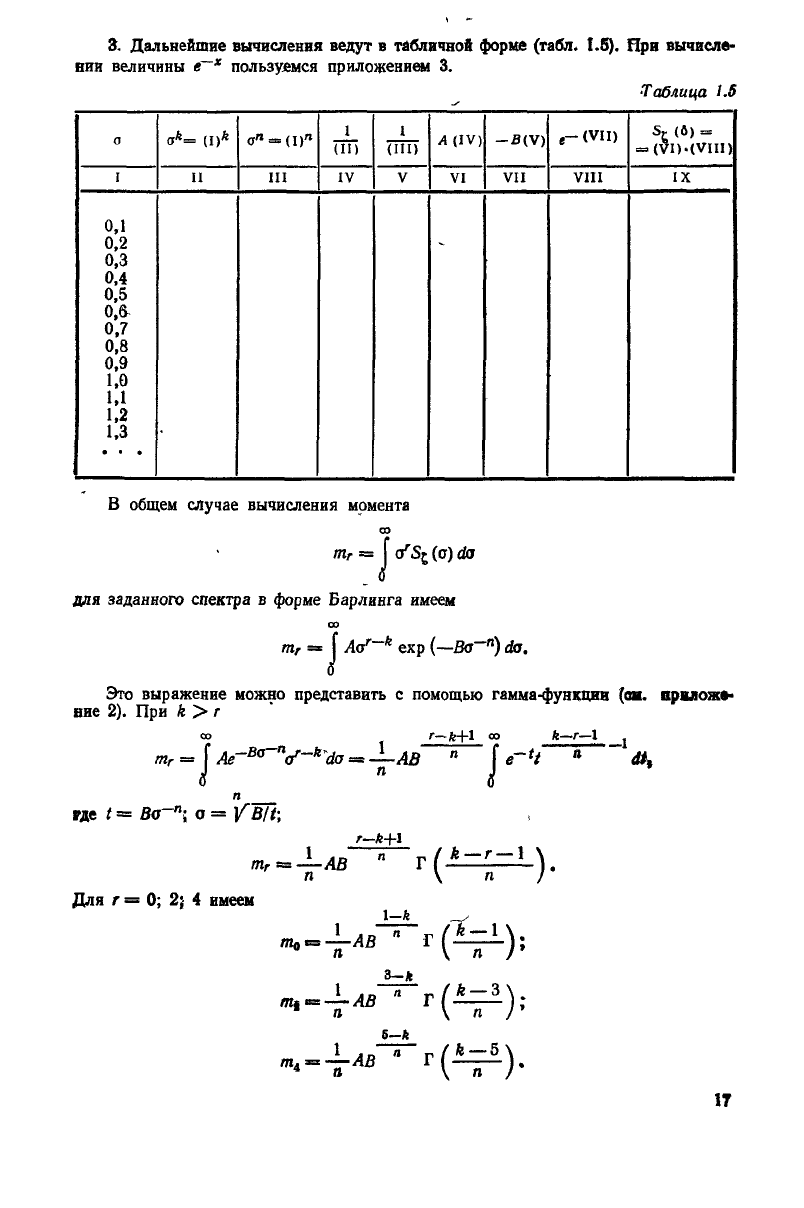
3. Дальнейшие вычисления

ведут

в табличной

форме

(табл.

1.5). Яри

вычисле-

нии

величины

е~

пользуемся приложением

Таблица

1.6

0,1

0.2

0,3

0,4

0,5

0,6-

0,7

0,8

0,9

1.0

1,1

1,2

1.3

• •

•

а*=

(D*

= (1)

III

(И)

(Пп

А (IV)

—B(V)

VII

е- (VII)

VIII

(в) =

(VI).

(VIII)

В общем

случае

вычисления момента

~ f

(о)

для заданного спектра

форме Барлинга имеем

= [

Ла

ехр

(—Ва~

)

da.

Это выражение можно представить

помощью гамма-функции

(он. приложе-

ние 2). При k > г

r~k+l

со k-r-l

где t

r—k+l

= -i-ЛВ

Для

r = 0; 2j 4 имеем

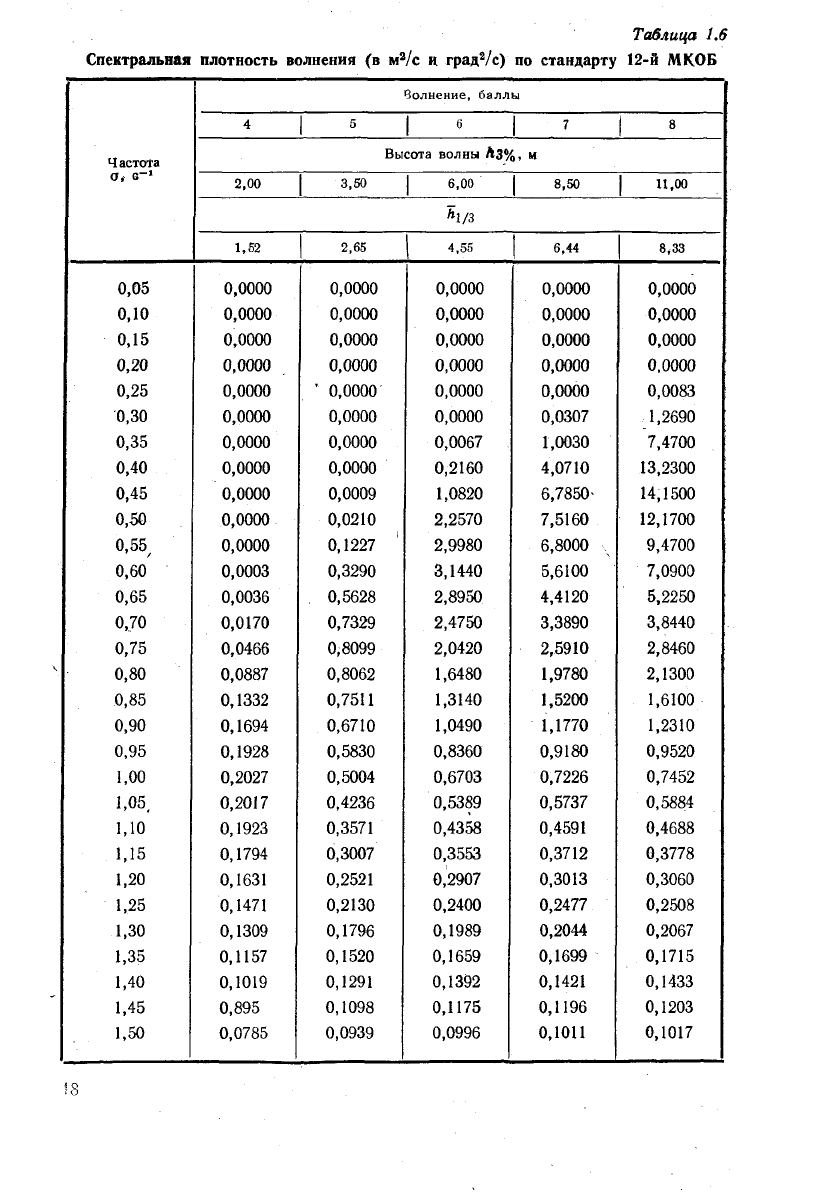
Таблица

1.6

Спектральная плотность волнения (в м

/с и град

/с) по стандарту 12-й

МКОБ

Частота

а.

а '

0,05

0,10

0,15

0,20

0,25

0,30

0,35

0,40

0,45

0,50

0,55

0,60

0,65

0,70

0,75

0,80

0,85

0,90

0,95

1,00

1,05.

1,10

1,15

1,20

1,25

1,30

1,35

1,40

1,45

1,50

Волнение, баллы

Высота волны Аз%,

2,00

3,50

6,00

8,50

11,00

*1/3

1,52

0,0000

0,0003

0,0036

0,0170

0,0466

0,0887

0,1332

0,1694

0,1928

0,2027

0,2017

0,1923

0,1794

0,1631

0,1471

0,1309

0,1157

0,1019

0,895

0,0785

2,65

0,0000

0,0009

0,0210

0,1227

0,3290

0,5628

0,7329

0,8099

0,8062

0,7511

0,6710

0,5830

0,5004

0,4236

0,3571

0,3007

0,2521

0,2130

0,1796

0,1520

0,1291

0,1098

0,0939

4,55

0,0000

0,0067

0,2160

1,0820

2,2570

2,9980

3,1440

2,8950

2,4750

2,0420

1,6480

1,3140

1,0490

0,8360

0,6703

0,5389

0,4358

0,3553

0,2907

0,2400

0,1989

0,1659

0,1392

0,1175

0,0996

6,44

0,0000

0,0307

1,0030

4,0710

6,7850-

7,5160

6,8000

5,6100

4,4120

3,3890

2,5910

1,9780

1,5200

1,1770

0,9180

0,7226

0,5737

0,4591

0,3712

0,3013

0,2477

0,2044

0,1699

0,1421

0,1196

0,1011

8(33

0,0000

0,0083

1,2690

7,4700

13,2300

14,1500

12,1700

9,4700

7,0900

5,2250

3,8440

2,8460

2,1300

1,6100

1,2310

0,9520

0,7452

0,5884

0,4688

0,3778

0,3060

0,2508

0,2067

0,1715

0,1433

0,1203

0,1017

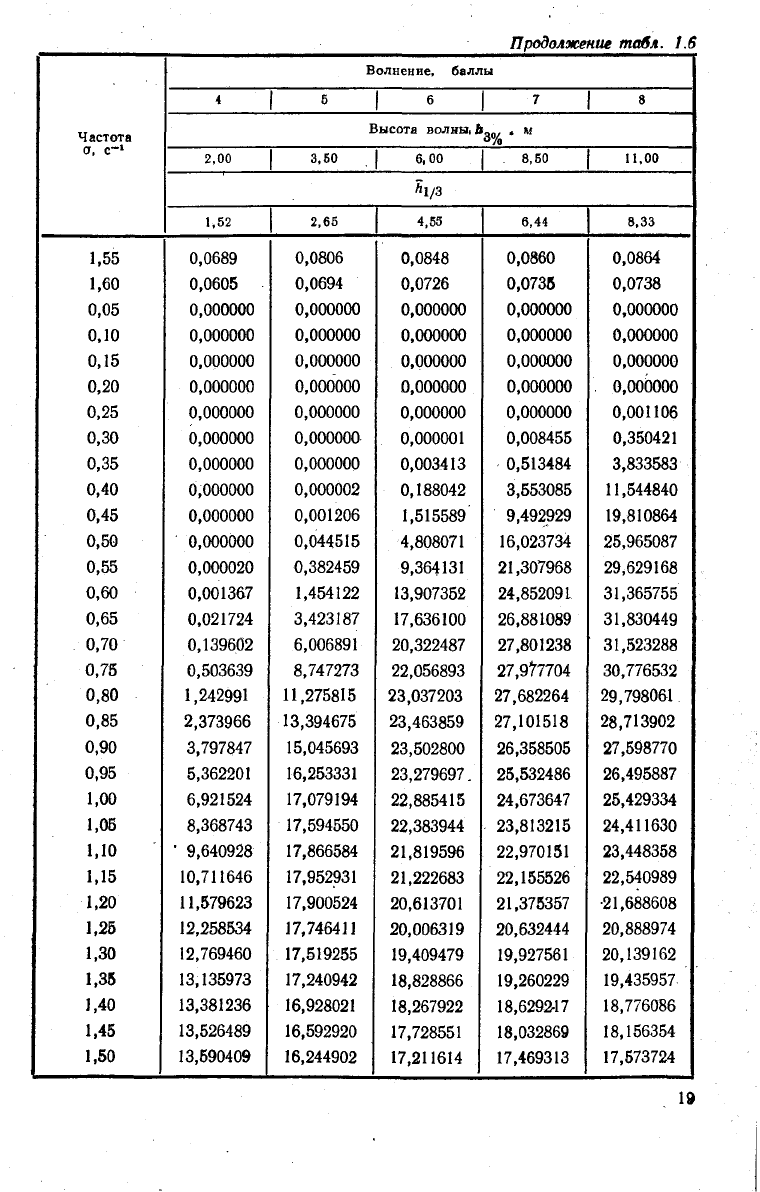
Продолжение

табл. 1.6

Частота

сг,

с *

1,55

1,60

0,05

0,10

0,15

0,20

0,25

0,30

0,35

0,40

0,45

0,50

0,55

0,60

0,65

0,70

0,75

0,80

0,85

0,90

0,95

1,00

1,05

1,10

1,15

1,20

1,25

1,30

1,36

1,40

1,45

1,50

Волнение,

баллы

2,00

1,52

0,0689

0,0605

0,000000

0,000020

0,001367

0,021724

0,139602

0,503639

1,242991

2,373966

3,797847

5,362201

6,921524

8,368743

9,640928

10,711646

11,579623

12,258534

12,769460

13,135973

13,381236

13,526489

13,590409

5 6

Высота волны, Ь

3,50

6,00

*1/8

2,65

0,0806

0,0694

0,000000

0,000002

0,001206

0,044515

0,382459

1,454122

3,423187

6,006891

8,747273

11,275815

13,394675

15,045693

16,253331

17,079194

17,594550

17,866584

17,952931

17,900524

17,746411

17,519255

17,240942

16,928021

16,592920

16,244902

4,55

0,0848

0,0726

0,000000

0,000001

0,003413

0,188042

1,515589

4,808071

9,364131

13,907352

17,636100

20,322487

22,056893

23,037203

23,463859

23,502800

23,279697.

22,885415

22,383944

21,819596

21,222683

20,613701

20,006319

19,409479

18,828866

18,267922

17,728551

17,211614

3»/

•

8,50

6,44

0,0860

0,0736

0,000000

0,008455

0,513484

3,553085

9,492929

16,023734

21,307968

24.85209L

26,881089

27,801238

27,977704

27,682264

27,101518

26,358505

25,532486

24,673647

23,813215

22,970151

22,155526

21,375357

20,632444

19,927561

19,260229

18,6292-17

18,032869

17,469313

11,00

8,33

0,0864

0,0738

0,000000

0,001106

0,350421

3,833583

11,544840

19,810864

25,965087

29,629168

31,365755

31,830449

31,523288

30,776532

29,798061

28,713902

27,598770

26,495887

25,429334

24,411630

23,448358

22,540989

•21,688608

20,888974

20,139162

19,435957

18,776086

18,156354

17,573724

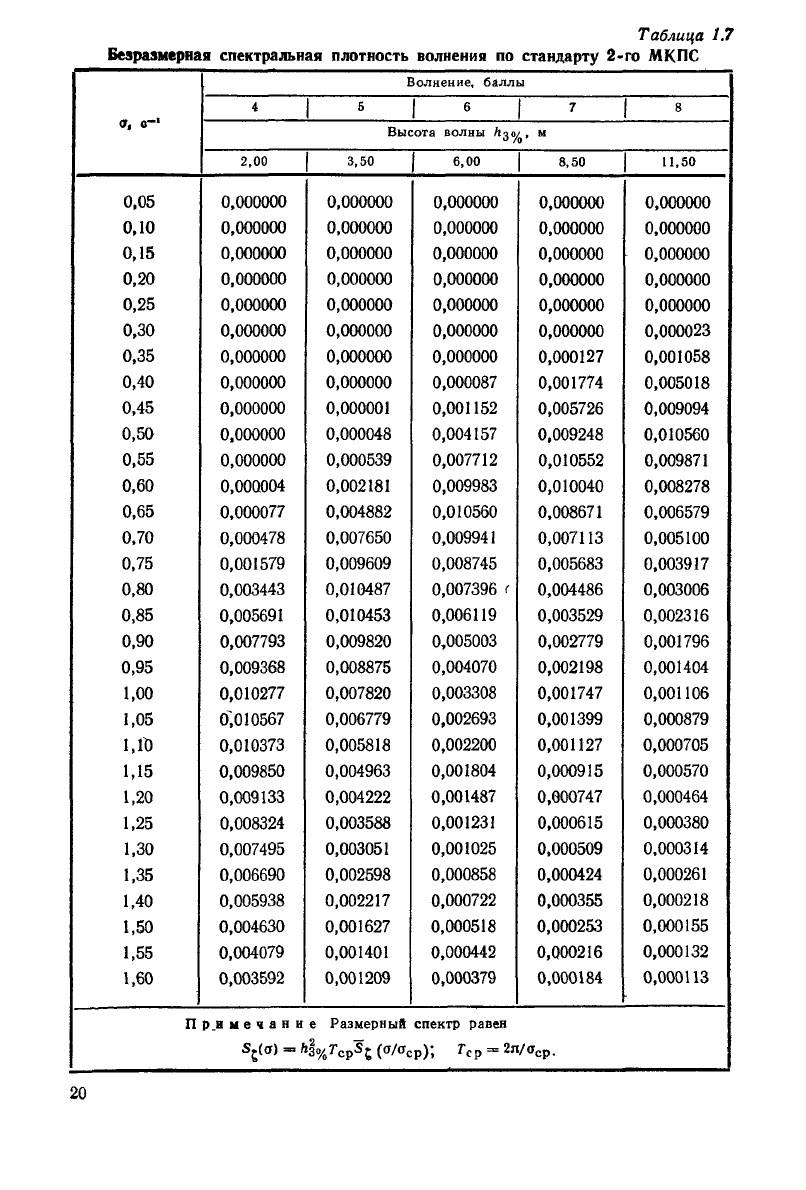
Таблица

1.7

Безразмерная

спектральная плотность волнения

по

стандарту

2-го

МКПС

СГ|

О""

0,05

0,10

0,15

0,20

0,25

0,30

0,35

0,40

0,45

0,50

0,55

0,60

0,65

0,70

0,75

0,80

0,85

0,90

0,95

1,00

1,05

1,Ш

1,15

1,20

1,25

1,30

1,35

1,40

1,50

1,55

1,60

Волнеыие,

баллы

7 8

Высота волны Л30/

2,00

0,000000

0,000004

0,000077

0,000478

0,001579

0,003443

0,005691

0,007793

0,009368

0,010277

б",010567

0,010373

0,009850

0,009133

0,008324

0,007495

0,006690

0,005938

0,004630

0,004079

0,003592

р.н и е ч а н и

«,)

= >

3,50

0,000000

0,000001

0,000048

0,000539

0,002181

0,004882

0,007650

0,009609

0,010487

0,010453

0,009820

0,008875

0,007820

0,006779

0,005818

0,004963

0,004222

0,003588

0,003051

0,002598

0,002217

0,001627

0,001401

0,001209

Размерный

3%7"

pSj

(o/o

6,00

0,000000

0,000087

0,001152

0,004157

0,007712

0,009983

0,010560

0,009941

0,008745

0,007396

0,006119

0,005003

0,004070

0,003308

0,002693

0,002200

0,001804

0,001487

0,001231

0,001025

0,000858

0,000722

0,000518

0,000442

0,000379

спектр равен

8,50

0,000000

0,000127

0,001774

0,005726

0,009248

0,010552

0,010040

0,008671

0,007113

0,005683

0,004486

0,003529

0,002779

0,002198

0,001747

0,001399

0,001127

0,000915

0,000747

0,000615

0,000509

0,000424

0,000355

0,000253

0,000216

0,000184

р);

ср

2п/а

ср

11,50

0,000000

0,000023

0,001058

0,005018

0,009094

0,010560

0,009871

0,008278

0,006579

0,005100

0,003917

0,003006

0,002316

0,001796

0,001404

0,001106

0,000879

0,000705

0,000570

0,000464

0,000380

0,000314

0,000261

0,000218

0,000155

0,000132

0,000113