Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

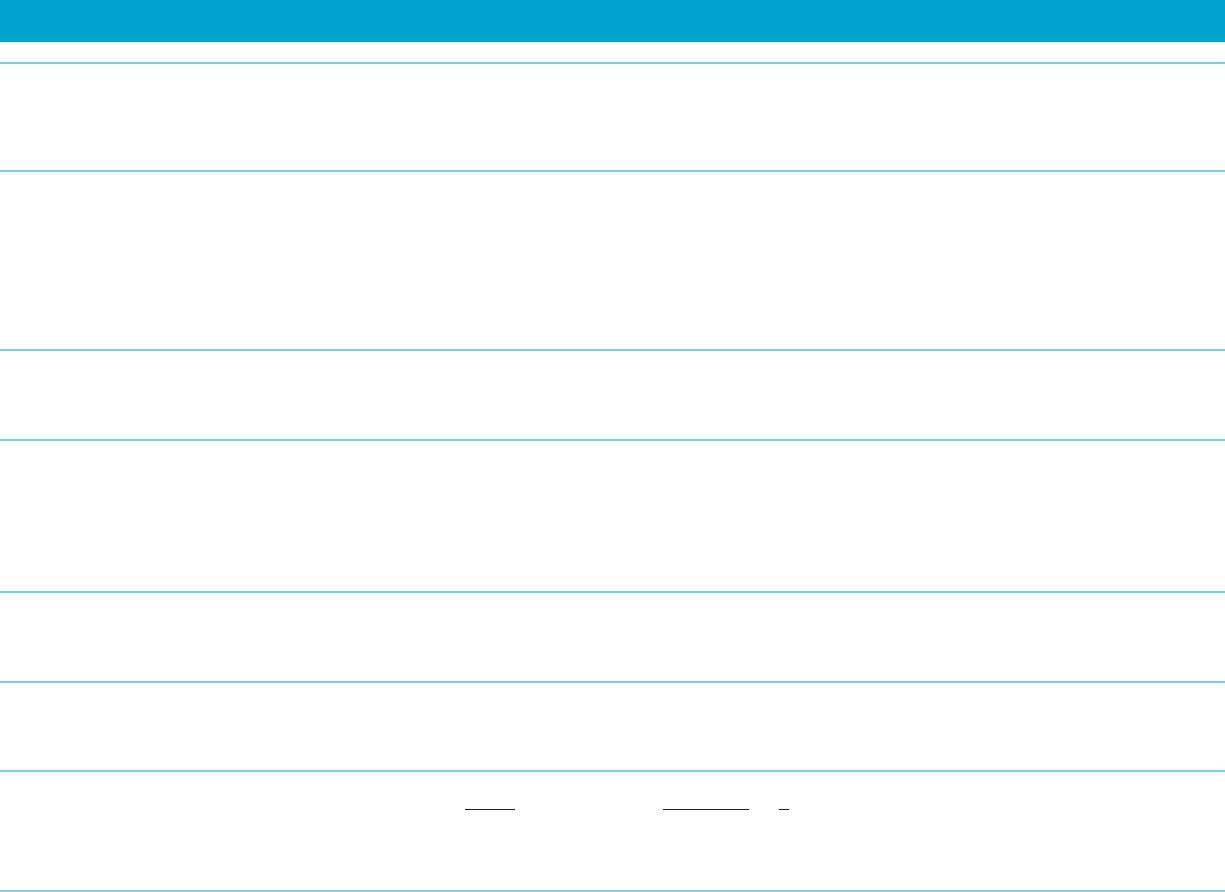
passes through the pair of points Pðc 2 0:001Þ and

Pðc 1 0:001Þ. For each c, calculate j1=c 2 mðcÞj to see

that mðcÞ is a good approximation of 1/c. Add the three

secant lines to your viewing window. For each of c 5 1,

3/2, and 2, add to the viewing window the line through

PðcÞ with slope 1/c. As we will see in Chapter 3, these

are the tanget lines at P(1), Pð3=2Þ, and Pð2Þ. It is likely

that they cannot be distinguished from the secant lines

in your plot.

Summary of Key Topics in Chapter 2

Limits

(Sections 2.12.2)

The expression lim

x-c

f ðxÞ5 ‘ means that f ðxÞ approaches ‘ as x approaches c.We

say that f has limit ‘ at c. More precisely, lim

x-c

f ðxÞ5 ‘ means that given, ε . 0;

there is a δ . 0 such that if 0 , jx 2 cj, δ, then jf ðxÞ2 ‘j, ε:

One-Sided Limits

(Section 2.2)

We say that f has

right limit ‘ at c if the domain of f contains the interval ðc; bÞ,and

given ε . 0; there is a δ . 0 such that if c , x , c 1 δ, then jf ðxÞ2 ‘j, ε: The deﬁ-

nition of left limit is similar. These limits are written lim

x-c

f ðxÞ and lim

x-c

f ðxÞ,

respectively. Left and right limits have properties similar to those of two-sided

limits. A function has limit ‘ at c if and only if it has left limit ‘ at c and right limit ‘

at c.

Uniqueness of Limits

(Section 2.2)

A function has at most one limit at a point: If lim

x-c

f ðxÞ5 ‘ and lim

x-c

f ðxÞ5 m,

then ‘ 5 m.

Algebraic Properties

of Limits

(Section 2.2)

a. lim

x-c

ðf ðxÞ1 gðxÞÞ5 lim

x-c

f ðxÞ1 lim

x-c

gðxÞ

b. lim

x-c

ðf ðxÞgðxÞÞ5 ðlim

x-c

f ðxÞÞ  ðlim

x-c

gðxÞÞ

c. lim

x-c

f ðxÞ=gðxÞ5 lim

x-c

f ðxÞ=lim

x-c

gðxÞ, provided that lim

x-c

gðxÞ 6¼ 0

d. lim

x-c

ðα  f ðxÞÞ5 α  lim

x-c

f ðxÞ for any constant α 2 R

Nonexistence of Limits

(Section 2.2)

If lim

x-c

f ðxÞ 6¼ 0 and lim

x-c

gðxÞ5 0, then lim

x-c

f ðxÞ=gðxÞ does not exist.

The Pinching Theorem

(Section 2.2)

If gðxÞ # f ðx Þ # hðxÞ and

lim

x-c

gðxÞ5 lim

x-c

hðxÞ5 ‘, then lim

x-c

f ðxÞ5 ‘.

Two Important

Trigonometric Limits

(Section 2.2)

lim

x-0

sinðxÞ

5 1 and lim

x-0

1 2 cosðxÞ

Continuity

(Section 2.3)

A function f is

continuous at c if lim

x-c

f ðxÞ5 f ðcÞ:

Summary of Key Topics 155

One-Sided Continuity

(Section 2.3)

A function f with

a domain that c ontains ½c; bÞ is said to be right-continuous at c

if lim

x-c

f ðxÞ5 f ðcÞ. The deﬁnition of left-continuous is similar. Left- and right-

continuous functions have properties similar to those f or continuous functions.

A function is continuous at c if and only if it is both left- and right-continuous

at c.

Properties of

Continuous Functions

(Section 2.3)

If the functions f and g are

continuous at c, then so are f 1 g, f 2 g, and f  g.

Furthermore, f /g is continuous at c provided that gðcÞ 6¼ 0:

The Intermediate

Value Theorem

(Section 2.3)

If f is

a continuous function with a domain that contains ½a; b,iffðaÞ5 α and

f ðbÞ5 β, and if γ is a real number between α and β, then there is a number c

between a and b such that f ðcÞ5 γ.

The Extreme

Value Theorem

(Section 2.3)

If f is

a continuous function with a domain that con tains ½a; b; then there are

numbers α and β in ½a; b such that f ðαÞ # f ðxÞ # f ðβÞ for all x in ½a; b:

Inﬁnite Limits and

Limits at Inﬁnity

(Section 2.4)

The expression lim

x-c

f ðxÞ5 N means that f (x) gets arbitrarily large as x

approaches c. More precisely, given K . 0, there is a δ . 0 such that if

0 , jx 2 cj, δ; then f (x) . K. The deﬁnitions of the one-sided inﬁnite limits

lim

x-c

f ðxÞ5 N and lim

x-c2

f ðxÞ5 N are similar. Analogous deﬁnitions exist for

lim

x-c

f ðxÞ52N; lim

x-c

f ðxÞ52N and lim

x-c

f ðxÞ52N: In any of these

cases, we say that x 5 c is a vertical asymptote of the graph of f.

The expression lim

x-N

f ðxÞ5 ‘ means that f (x) gets arbitrarily close to ‘ as x

gets arbitrarily large through positive values. More precisely, given ε . 0; there is

K . 0 such that if x . K; then jf ðxÞ2 ‘j, ε: The deﬁnition of lim

x -2N

f ðxÞ5 ‘

is analogous. In either case, we say that y 5 ‘ is a horizontal asymptote of the graph

of f.

Limits of Sequences

(Section 2.5)

The expression

lim

j-N

5 ‘

means that a

gets arbitrarily close to the real number ‘ as the positive integer

variable j gets arbitrarily large. More precisely, given ε . 0; there is a J . 0 such

that if j . J, then ja

2 ‘j, ε: We say that the sequence fa

g is convergent.

The algebraic properties of limits discussed in Section 2.2 are also valid for

limits of sequences, as is the Pinching Theorem.

The Monotone

Convergence Property

(Section 2.6)

A sequence fa

g is said to be monotone if it is decreasing (a

j11

# a

for every j)or

if it is increasing (a

j11

$ a

for every j). A sequence fa

g is said to be bounded if

there is a K such that ja

j, K for every j. The Monotone Convergence Property of

the real number system states that every monotone bounded sequence is

convergent.

156 Chapter 2 Limits

Exponential Functions

(Section 2.6)

If a . 0

and x is irrational, then we may deﬁne a

5 lim

x-N

where fx

g is a sequence of rational numbers that converges to x. All the usual

rules of exponents remain valid:

x1y

5 a

; a

; and ða

5 a

The Number e

(Section 2.6)

The number e is

deﬁned by

e 5 lim

n-N



It is an irrational number with a decimal representation that begins with

2.7182818284590452. In general, for any real number u,

5 lim

x-N



Logarithms

(Section 2.6)

If a is

a positive number not equal to 1, then the exponential function with base a,

namely x/ a

, is invertible. The inverse function is written as y/log

ðyÞ if a 6¼ e.

When e is used as a base, x/e

is called the exponential function, and its inverse,

which is called the natural logarithm function, is denoted by y/lnðyÞ. The natural

logarithm satisﬁes the two identities

lnðxyÞ5 lnðxÞ1 lnðyÞ

and

lnðx

Þ5 p lnðxÞ:

Exponential

Growth and Decay

(Section 2.6)

A quantity P(t)

grows exponentially if PðtÞ5 Ae

for positive constants A and k.

The doubling time of P is given by

T 5

lnð2Þ

and has the property that, for every t,

Pðt 1 TÞ5 2  PðtÞ:

A quantity mðtÞ decays exponenti ally if mðtÞ5 Aexpð2 λtÞ for positive con-

stants A and λ. The half-life

τ 5

lnð2Þ

has the property that, for every t,

mðt 1 τÞ5

 mðtÞ:

Summary of Key Topics 157

Review Exercises for Chapter 2

c In each of Exercises 1230, a function f (x) and a value c

are given. Determine whether or not lim

x-c

f ðxÞ exists. If the

limit does exist, compute it. b

1. f ðxÞ5 1=sinð2xÞ, c 5 π

2. f ðxÞ5 x

2 6x 1 8, c 5 5

3. f ðxÞ5 ðx

1 7x 1 10Þ=ðx 1 5Þ, c 524

4. f ðxÞ5 ðx 2 18Þ=ðx 1 2Þ, c 5 3

5. f ðxÞ5 ðx

2 36Þ=ðx 1 6Þ, c 526

6. f ðxÞ5 ðx2 1Þ

=ðx 1 1Þ, c 521

7. f ðxÞ5 ðx 1 5Þ=ðx

2 25Þ5, c 525

8. f ðxÞ5

2 5x 1 6

x 2 2

if x , 2

sec ðπx=2Þ if x $ 2

c 5 2

9. f ðxÞ5

2 7

if x # 5

1 2x 2 35

2 8x 1 15

if x . 5

c 5 5

10. f ðxÞ5 jxj2 x 1 j2 xj1

ﬃﬃﬃﬃﬃ

, c 523

11. f ðxÞ5 3x 1 tanðπxÞ; c 5 1=2

12. f ðxÞ5 3x 1 tanðπxÞ, c 5 2

13. f ðxÞ5 x=jxj, c 523

14. f ðxÞ5 x=jxj, c 5 0

15. f ðxÞ5 x=sinðxÞ, c 5 0

16. f ðxÞ5 sinðxÞ=x, c 5 π=6

17. f ðxÞ5 x

= 1 2 cosðxÞðÞ; c 5 0

18. f ðxÞ5 jxjcscðxÞ; c 5 0

19. f ðxÞ5 ðx

1=3

1 28Þ=

ﬃﬃﬃ

, c 5 64

20. f ðxÞ5 ðx

2 9Þ=ðx23Þ

, c 5 3

21. f ðxÞ5 ð1 2 cosðxÞÞ=x, c 5 0

22. f ðxÞ5 sinð2xÞ=x

, c 5 0

23. f ðxÞ5 sinð7xÞ=sinð3xÞ, c 5 0

24. f ðxÞ5 x sinðxÞ=ðcos ð xÞ2 1Þ, c 5 0

25. f ðxÞ5 ð1 2 cosðxÞÞ=sinðxÞ, c 5 0

26. f ðxÞ5 tanðxÞ=x, c 5 0

27. f ðxÞ5 tanð3xÞ=x, c 5 0

28. f ðxÞ5 sinðxÞ=x, c 5 π=2

29. f ðxÞ5 ðsinðxÞ1 cosðxÞÞ=x

30. f ðxÞ5 x=ð1 2 cosðxÞÞ, c 5 0

c In Exercises 31234, use algebraic manipulation to evalu-

ate

the given limit. b

31. lim

x-4



2 16

ﬃﬃﬃ

2 2



32. lim

x-9



x 2 3

ﬃﬃﬃ

2 9



33. lim

x-0

12x

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 6x

2 1

34. lim

x-0



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

5 1 x

ﬃﬃﬃ



c In Exercises 35240, evaluate the given one-sided limits. b

35. lim

x-5

x 2 5

jx 2 5j

36. lim

x-5

x 2 5

jx 2 5j

37. lim

x-4

 ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

16 2 4x

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

16 2 x



38. lim

x-0

ﬃﬃﬃ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

sinðxÞ

39. lim

x-0

ﬃﬃﬃﬃﬃ

40. lim

x-ðπ=2Þ

ð1=

ﬃﬃﬃ

tanðxÞ

c In Exercises 41254, determine whether or not the given

limit exists. If the limit does exist, compute it. Where

appropriate, answer with N or 2N. b

41. lim

x -2N

ð9 2 e

42. lim

x -2N

ðπ 2 e

23x

43. lim

x-N

ðπ 1 2

44. lim

x -2N

ð7 2 2

45. lim

x-N

ðcosðxÞ1 2e

46. lim

x-N

1 2x 1 1

1 x

1 x 1 2

47. lim

x-N

1 2x 1 1

1 x 1 2

48. lim

x-N

1 x 1 3

1 x 1 2

49. lim

x-N

3x 1 2

1 2

50. lim

x-N

10 1 lnðxÞ

5 1 lnðxÞ

51. lim

x-N

ð12 1=xÞ

52. lim

x - 2N



lnð2Þ



53. lim

x-0

x cos

ð1=xÞ

54. lim

x-0

x cscðxÞcosð1=xÞ

c In each of Exercises 55258, calculate how close x needs

be to c to force f (x) to be within 0.01 of ‘. b

55. f ðxÞ5 x 1 1 c 521 ‘ 5 0

56. f ðxÞ5 2x 1 13 c 527 ‘ 521

57. f ðxÞ5 2x

c 525 ‘ 5 50

58. f ðxÞ5

4x 2 3ifx # 1

if x . 1

c 5 1 ‘ 5 1



158 Chapter 2 Limits

c In each of Exercises 59262, determine whether the given

function f has a continuous extension F that is deﬁned on the

entire real line. If it does, answer with the value of F at the

point that is not in the domain of f. b

59. f ðxÞ5

2 x=

ﬃﬃﬃﬃ

ﬃ

if x , 0

sinðxÞ=x if x . 0



60. f ðxÞ5

ðx

2 3x 1 2Þ=ðx 2 2Þ if x , 2

x 1 1ifx . 2



61. f ðxÞ5

ðx

2 1Þ=ðx 1 1Þ if x ,21

1 x 2 2ifx .21



62. f ðxÞ5 lim

x-0

sin

ð4x

Þ=x

c In each of Exercises 63268, ﬁnd all horizontal and vertical

asymptotes for the graph of the function that is deﬁned by the

given expression. b

63. ðx 1 4Þ=ðx 1 3Þ

64. ðx

1 9Þ=ðx

2 9Þ

65. ð2x 1 3Þ=ðx

1 1Þ

66. 3x

=ðx

2 7x 1 6Þ

67. ð3x

2 9x 1 6Þ=ðx

1 x 2 2Þ

68.

expð5xÞ1 expð25xÞ

expð5xÞ2 expð25xÞ

c In Exercises 69272, simplify the given expression. b

69. ð1=27Þ

22=3

70.

ﬃﬃﬃ

ﬃﬃ



ﬃﬃﬃ

71. ð2

 4

3=2

72.

ﬃﬃﬃ

ﬃﬃ



ﬃﬃ

c In Exercises 73276, rewrite the given expression without

using any exponentials or logarithms. b

73. log

ð8  4

 2

122x

74. expðlog

ð6Þ=log

ðeÞÞ

75. log

ﬃﬃ

ðlog

ð64ÞÞ

76. ð

ﬃﬃﬃ

lnð4x

77. Solve for x: ð3

5 18  2

78. Solve for x:4

5 2  8

79. Describe the function f ðxÞ5 lim

y-x

byc2 lim

y-x

byc :

c In each of Exercises 80285, calculate lim

n-N

for the

given sequence fa

g: b

80.

3n 1 2

n 1 6

81. f100

1=n

82.



n1 2



1=n

()

83. 5

84.

2 4

1 4



85.

2 5

1 5



86. The volume V(t) of harvestable timber in a young forest

grows exponentially; that is, VðtÞ5 Ae

for positive

constants A and k. If the yearly rate of increase is equal

to 3.5%, then what percentage increase is expected in 10

years?

87. Learning curves are sometimes exponential in form.

Suppose that after t weeks in a classroom, the class

average (out of 100) on a standard aptitude test is

AðtÞ5 100ð1 2 e

Þ:

A particular class has an average score of 75 after 6

weeks. In how many more weeks will the average score

exceed 90?

88. Moore’s law (after Gordon Moore, cofounder of Intel)

asserts that the number of transistors that can be pressed

onto a ﬁxed area doubles every 18 months. Assuming that

this observation remains valid, in how many months will

the number of transistors that can be pressed onto a ﬁxed

area increase by a factor of 100?

89. The amount of

226

Ra decays exponentially. The half-life

226

Ra is 1620 years. An area is contaminated with a

level that is ﬁve times greater than the maximum safe

level. Without a cleanup, how long will this area remain

unsafe?

c In Exercises 90296, which concern radiocarbon dating, m

refers to the mass of

C that the analyzed sample had at the

moment of death. (Refer to the instructions for Exercises

95298 of Section 2.6 for further details.) The half-life of

Cis

5700 years. b

90. The Shroud

of Turin is a cloth believed by some to be the

burial cloth of Jesus. In 1988, strands of the cloth were

given to four different institutions for dating. Each

institution declared the Shroud of Turin to be a medieval

forgery from around 1325 CE. Approximately what per-

centage of m

was measured?

91. In 1995, the Dead Sea Scroll text known as 4Q258 was

radiocarbon dated. The result suggested a date of about

180 CE. Paleographic evidence had placed the date at

about 100 BCE.

a. What fraction of m

would have validated the

paleographic evidence?

b. What fraction was actually found?

92. The oldest North American mummy, the Spirit Cave

Man, was discovered near Fallon, Nevada in 1940. In the

days before radiocarbon dating, Nevada State Museum

anthropologists estimated the mummy to be about 2000

years old. In 1996, radiocarbon dating of hair and textile

Review Exercises 159

strands that were buried with the mummy placed the age

at 9400 years. What fraction of m

was found?

93. On September 19, 1991, a mummiﬁed human body was

discovered in an Austrian glacier near the Tisenjoch pass.

Radiocarbon analysis has shown that the Iceman, as he

has come to be called, died around 3325 BCE. What

percentage of m

was measured?

94. After World War II, to avoid imprisonment for selling

art work to the Nazis, Dutch artist Han van Meegeren

(18891947) confessed to having forged the paintings he

sold as Vermeers. Given that Vermeer died in 1675, what is

the maximum percentage of m

that could have been found

in the pigments of one of his paintings in 1945? What

percentage of m

would fakes from 1930 have had in 1945?

95. When samples, all having equal

C content, were

extracted from pigments coming from different areas of a

cave drawing in Chauvet, one sample had

C content

that was 1.837 times greater than the

C content found in

the other samples. About how many years after the ori-

ginal work was the “touch-up” work done?

96. Cro-Magnon Man migrated to Europe about 40,000 years

ago. For a long time scientists believed that the Nean-

derthals vanished soon afterwards. However, recent

radiocarbon dating of a European Neanderthal fossil

resulted in a

C value of 0.026 m

. For about how long

did the European Neanderthals and Cro-Magnons coex-

ist (at the least)?

160 Chapter 2 Limits

GENESIS

DEVELOPMENT2

Mathematical standards did not always require con-

cepts to be clearly deﬁned and resul ts to be correctly

demonstrated. Even though the limit is basic to calcu-

lus, a rigorous treatment of limits was not developed

until the 19th century. By that time, most of the topics

that are studied in a modern calculus course had long

been known. For 200 years, mathematicians relied on

an intuitive understanding of limits, but it eventually

became clear that a more precise viewpoint was

necessary.

The Controversy over Inﬁnitesimals

The fundamental concept of differential calculus is the

limit

‘ 5 lim

Δx-0

f ðc 1 ΔxÞ2 f ð cÞ

Δx

We have already used a limit of this form in our dis-

cussion of instantaneous velocity (see Section 2.1). We

will consider such limits in much greater detail in

Chapter 3. For a long time, the most common approach

to such a limit was through the mechanism of inﬁnite-

simals (quantities that are inﬁnitely smal l). The limit ‘

was envisioned as a quotient in which the numerator

was the inﬁnitesimal increment dy in the variable

y 5 f ð x Þ caused by incrementing the value c of the

variable x by the inﬁnitesimal amount dx. For example,

if y 5 x

, then

dy 5 ðc1dxÞ

2 c

5 2c  dx 1 ðdxÞ

;

and

‘ 5

2c  dx 1 ðdxÞ

5 2c 1 dx:

Under the rules of inﬁnitesimal algebra, a non-

inﬁnitesimal quantity remains unchanged when an

inﬁnitesimal is added to it. Thus the limit ‘ is 2c.

Although the inﬁnitesimal method yields the cor-

rect answer, a logical dilemma is present: If

2c 1 dx 5 2c, then dx is really 0, in which case, the

quotient

is not algebraically permitted. On the other

hand, if the quotient

is permitted because dx 6¼ 0,

then 2c 1 dx 6¼ 2 c.

In 1734, George Berkeley (16851753), Bishop of

Cloyne, Ireland, published The Analyst, a tract addressed

to an “inﬁdel mathematician,” generally presumed to be

the astronomer Edmond Halley. In it, Berkeley attacked

the hypocrisy of those who scorned religious belief but

who put their faith in inﬁnitesimals, which were not then

precisely conceived or employed in a consistent manner:

The Imag ination, which faculty derives from sense,

is very much strained and puzzled to frame clear

ideas of the least particles of time . . . The further

the mind analyseth and pursueth these fugitive ideas,

the more it is lost and bewildered; the objects at ﬁrst

ﬂeeting and minute, soon vanishing out of sight . . . I

have no controversy about your conclusions, but

only about your logic and method: how you

demonstrate? what objects you are conversant with,

and whether you conceive them clearly? what prin-

ciples you proceed upon; how sound they may be;

and how you apply them?

The criticisms of Berkeley initiated a ﬂurry of

interest in the foundations of calculus. There was also a

second stimulus that pointed to the need for more

precision. In 1747, Jean le Rond d’A lembert

(17171783) published both the law governing the

motion of a vibrating string and its general solution.

Although d’Alembert’s equation did not come into

question, his solution to it did. In 1748, Leonhard Euler

and, in 1753, Daniel Bernoulli (17001782) proposed

different solutions. Mathematics was in the embarras-

sing situation of having three of its greatest proponents

debate mathematical truths as they would points of

metaphysics.

Bolzano and the Intermediate Value Theorem

By the end of the 18th century, mathematicians had

started to look for ways to formulate the concepts and

theorems of calculus without reference to inﬁnitesimals.

The approaches taken by Bernard Bolzano

(17811848) and Augustin-Louis Cauchy (17891857)

stand out. Bolzano gave the ﬁrst “modern” deﬁnition of

“continuity” in his 1817 paper on the Intermediate

Value Theorem. In Bolzano’s deﬁnition, f is continuous

at x “if the difference f ðx 1 ωÞ2 f ðxÞ can be made

smaller than any given magnitude by taking ω as small

as is wished.” In the title of his paper, Bolzano stressed

that he was giving an analytic proof of the Intermediate

Value Theorem. The theorem was known previously,

161

but it was always considered self-evident on geometric

grounds. Bolzano realized that the theorem must

depend on both the properties of the functions under

consideration and on the completeness property of the

real numbers. Here, for the ﬁrst time, we ﬁnd explicit

awareness that a completeness property of the real

number system requires proof.

One of Bolzano’s approaches to completeness was

the least upper bound property of the real number

system. Let S be a bounded set of real numbers. A

number U is said to be the least upper bound of S if U is

the least number such that x # U for each x in S.

For example, if S 5 fx 2 R : x

, 2g, then every ele-

ment x of S satisﬁes jxj,

ﬃﬃﬃ

,so

ﬃﬃﬃ

is an upper bound

of S. It is not hard to show that no smaller number is an

upper bound of S.

The least upper bound property states that every

nonempty set of real numbers that is bounded above

has a least upper bound. The rational number system Q

does not have this property. For example, if

5 fx 2 R : x

, 2g, then every rational number larger

than

ﬃﬃﬃ

is an upper bound but not a least upper bound.

The Least Upper Bound Property, the Monotone

Convergence Property, and the nested interval prop-

erty, which was discu ssed in the Genesis & Development

for Chapter 1, are equivalent properties of the real

number system.

Bolzano’s position was Professor of Theology at

the University of Prague. However, after 1819 when he

was dismissed for heresy, he was subjected to police

supervision, and his writing was curtailed. In addition

to his careful derivation of the Intermediate Value

Theorem from the least upper bound property of the

real numbers, he made several original discoveries

concerning the foundations of mathematical analysis.

Nevertheless, because he worked and published in

relative obscurity, his ideas did not receive their due

until long after his death.

Cauchy and Weierstrass

Credit, if not priority, for the movement toward rigor in

calculus must be given to Augustin-Louis Cauchy, the

most prominent mathematician in the greatest center

of mathematics of his day. His Cours d’Analyse (1821)

and subsequent Ecole Polytechnique lecture notes

alerted a generation of mathematicians to the possibi-

lity of attaining a rigor in calculus that was compar able

to that of classical geometry. Although the verbal

deﬁnition of “limit” that Cauchy gave in his Cours was

scarcely better than that given by his predecessors, and

certainly worse than that given by Bolzano, it is clear

from his translation of his verbal deﬁnition into math-

ematical inequalities that he meant exactly the deﬁni-

tion of limit as given in Section 2.2. Indeed, it was

Cauchy who introduced the symbols and ε and δ (with

ε standing for “erreur” and δ for “diff

erence”). Many of

the theorems of calculus received their ﬁrst modern

formulations in Cauchy’s work.

A completely correct presentation of the founda-

tions of calculus was ﬁnally given by Karl Weierstrass.

We have already mentioned Weierstrass in the Genesis

& Development for Chapter 1 in connection with his

construction of the real number system. Weierstrass had

an unusual career as a research mathematician. Born in

the village of Ostenfelde, Weierstrass entered the Uni-

versity of Bonn in 1834 as a law student. He did not

begina serious study of mathematics until 1839, when he

was 24. From 1840 until 1856, Weierstrass taught science,

mathematics, and physical ﬁtness at a high school. He

became a professor at the University of Berlin in 1864, at

the relatively advanced age of 49. It was in his lectures at

the University of Berlin that Weierstrass clariﬁed the

fundamental structures of mathematical analysis. Of

primary importance in this regard was Weierstrass’s

careful delineation of different types of convergence. In

the words of David Hilbert (18621943),

It is essentially a merit of the scientiﬁc activity of

Weierstrass that mathematicians are now in com-

plete agreement and certainty concerning types of

analytic reasoning based on the concepts of irra-

tional number and, more generally, limit.

At one time, mathematical theory required suc-

cessive revision as mathematicians delved deeper into

existing theory. The formulation of a precise deﬁnition

of limit has given a permanent character to the foun-

dation of calculus.

162 Chapter 2 Limits

CHAPTER 3

The Derivative

Suppose that c is a point in the domain of a function f. As the independent

variable x of f (x) changes from c to c 1 Δ x, the value of f (x) changes from f (c)to

f (c 1 Δ x). The average rate of change of f (x) is obtained by dividing the change in

f (x) by the change in x:

f ðc 1 Δ x Þ2 f ðcÞ

Δx

ð3:0:1Þ

This average rate of change over the interval ½c; c 1 Δx can be useful, but there are

times when the rate of change at the particular value c has greater importance.

Because Δx appears in the denominator of form ula (3.0.1), we cannot simply set

Δx 5 0 to obtain the rate of change of f at c. Inste ad, we let Δx tend to 0 and use the

limit

lim

Δx-0

f ðc 1 ΔxÞ2 f ðcÞ

Δx

ð3:0:2Þ

to deﬁne the instantaneous rate of change of f (x)atx 5 c. We call limit (3.0.2) the

derivative of f at c and denote it by f

ðcÞ. As we will see, f

ðcÞ also represents the

slope of the tangent line to the graph of the equation y 5 f (x) at the point (c, f (c)).

The branch of mathematics devoted to the study of derivatives is called dif-

ferential calculus. In this chapter, you will learn methods for evaluating the deri-

vatives of common functions. Because the direct calculation of limits such as (3.0.2)

can be difﬁcult, we will develop rules that allow us to compute derivatives without

actually referring to limits.

PREVIEW

163

3.1 Rates of Change and Tangent Lines

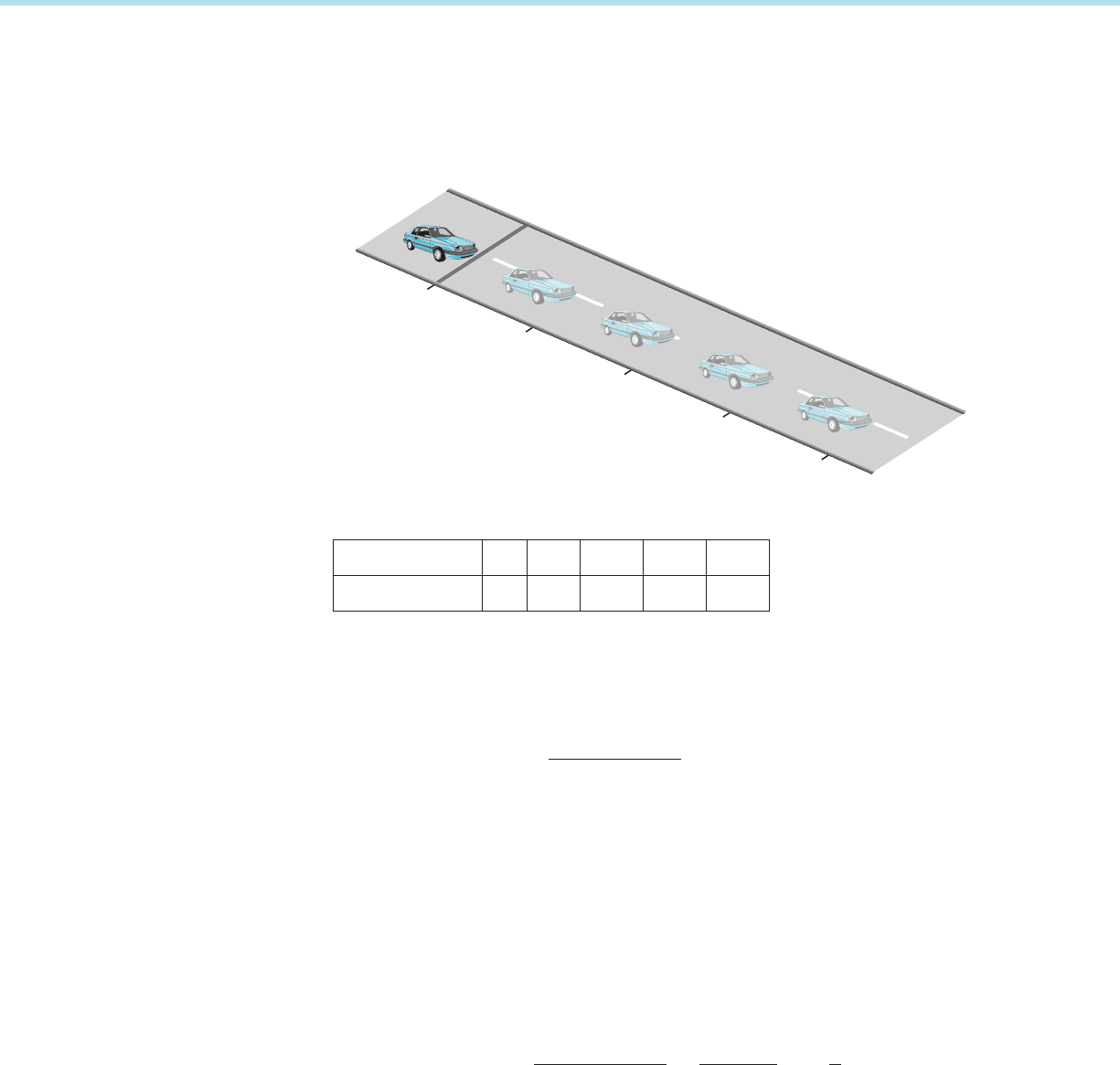
Imagine car A driving down a road, as in Figure 1. We are standing at the side of

the road, and we wish to determine the velocity of car A at any given moment.

Here is how we proceed. We record the position p(t) of car A as time elapses. Time

t 5 0 corresponds to the time that our observations begin (see Table 1).

Time (seconds) 01

2 3 4

Distance (feet) 0 50 100 150 200

Table 3.1

Anal

yzing the speed of car A is simple because it is traveling at a constant rate:

50 feet in 1 second, 100 feet in 2 seconds, 150 feet in 3 seconds, 200 feet in 4

seconds, and so on. At all observed times,

rate 5

distance traveled

time elapsed

5 50 feet= second:

Suppose that a second car B travels down the road, as in Figure 2, with position

p(t) 5 8t

feet if t is measured in seconds. Some values of p(t) are recorded in

Table 2.

With each passing second, car B covers more ground than in the previou s

second. For example, car B moves 8 2 0 5 8 feet in the ﬁrst second, 32 2 8 5 24 feet

in the second second, 72 2 32 5 40 feet in the third second, and 128 2 72 5 56 feet in

the fourth second. In other words, car B is accelerating. Because the velocity of car

B is ever changing, how can we calculate the velocity of car B at a given instant of

time, say t 5 1?

To begin to answer this question, we can calculate the averag e velocity of car B

between times t 5 1 and t 5 2. This is

rate 5

distance traveled

time elapsed

ð32 2 8 Þft

ð2 2 1Þs

5 24

200

150

100

t  0

t  1

t  2

t  3

t  4

m Figure 1

164 Chapter

3 The Derivative