Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

Proof. To prove equation (3.2.7), we start with the deﬁnition of the deriv ative and

calculate as follows:

sinðxÞ

5 lim

Δx-0

sinðx 1 ΔxÞ2 sinðxÞ

Δx

5 lim

Δx-0



sinðxÞcosðΔxÞ1 cosðxÞsinðΔxÞ



2 sinðxÞ

Δx

Addition Formula ð1:6:4Þ

5 lim

Δx-0

sinðxÞðcosðΔxÞ2 1Þ

Δx

1 lim

Δx-0

cosðxÞsinðΔxÞ

Δx

52sinðxÞ lim

Δx-0

ð1 2 cosðΔxÞÞ

Δx

1 cosðxÞ lim

Δx-0

sinðΔxÞ

Δx

52sinðxÞ0 1 cosðxÞ1 Equations ð3:2: 6 Þ

5 cosð x Þ:

In a similar manner, we de rive formula (3.2.8) by using Addition Formula (1.6.4)

for the cosine, written in the form cosðx 1 ΔxÞ5 cosðxÞcosðΔxÞ2 sinðxÞsin ðΔxÞ;

together with equations (3.2.6):

cosðxÞ 5 lim

Δx-0

cosðx 1 ΔxÞ2 cosðxÞ

Δx

5 lim

Δx-0



cosðxÞcosðΔxÞ2 sinðx ÞsinðΔxÞ



2cosðxÞ

Δx

5 lim

Δx-0

cosðxÞcosðΔxÞ2 cosðxÞ

Δx

1 lim

Δx-0

2sinðxÞsinðΔx Þ

Δx

52cosðxÞ lim

Δx-0

1 2 cosðΔxÞ

Δx

2 sinðxÞ lim

Δx-0

sinðΔxÞ

Δx

52cosðxÞ0 2 sinðxÞ1

52sinðxÞ:

’

⁄ EX

AMPLE 5 The derivative formula

sinðxÞ5 cosðxÞ

was obtained by algebraic manipulations involving trigonometric identities. Find

visual evidence for its correctness.

Solution By

deﬁnition,

sinðxÞ5 lim

Δx-0

sinðx 1 ΔxÞ2 sinðxÞ

Δx

We can approximate this limit by selecting a small value for Δx. Figure 9a illus-

trates the approximation when Δx 5 0.25. For this choice of Δx, which is not

612345

0.5

1.0

1.0

0.5

x  0.25

y  cos(x)

y 

sin(x  x)  sin(x)

x

m Figure 9a

3.2 The Derivative 185

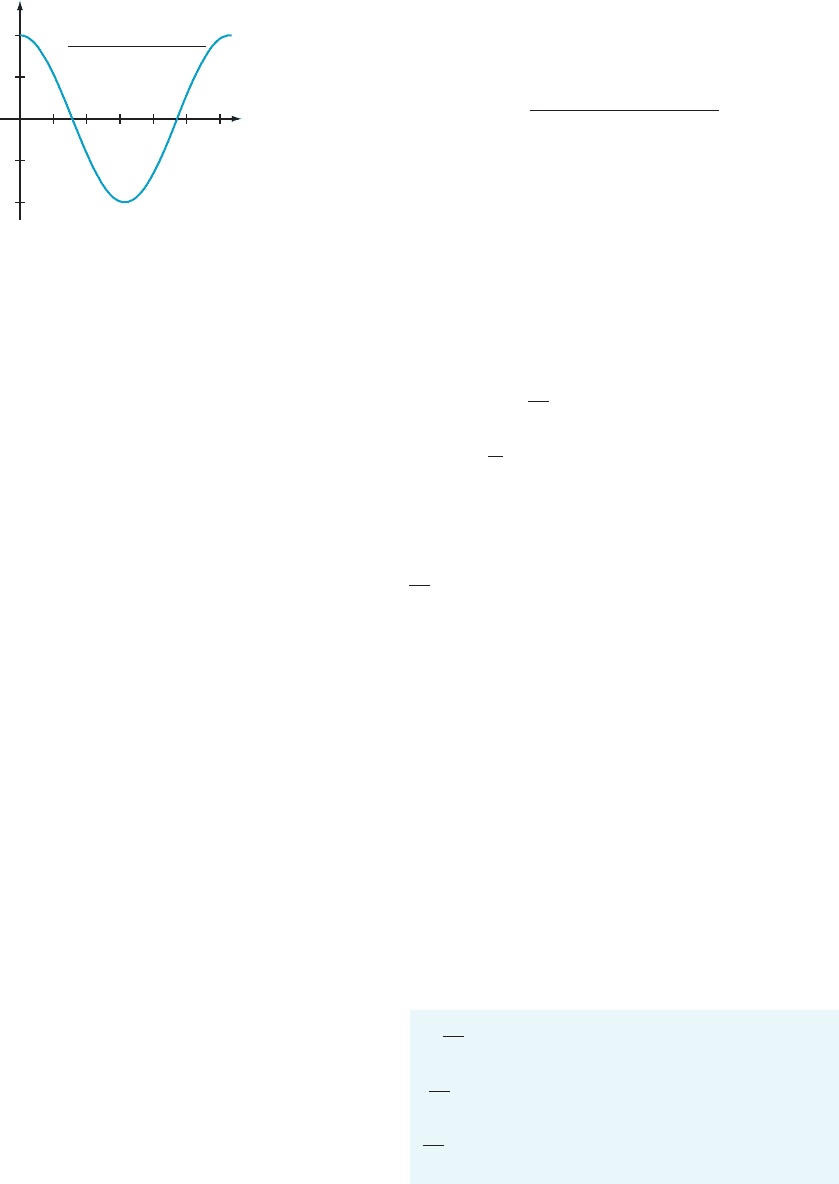
particularly small, the approximation is not extremely accurate. Nevertheless, it

does give the idea. In Figure 9b, we set Δx 5 10

and graphed both the approx-

imate derivative

sinðx 1 10

Þ2 sinðx Þ

and the exact derivative cos (x). Only one curve appears in the ﬁgure because the

amount by which the approximate derivative deviates from cos (x) is too minute to

be displayed.

Derivatives of

Expressions

In calculus, we often use expressions as a shorthand for functions. Thus the

expression x

1 cosð

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

x 1 1

Þ is frequently interpreted to be the function f deﬁned

by f (x) 5 x

1 cosð

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

x 1 1

Þ for all values of x for which the expression makes sense.

With such an inte rpretation, we will write



1 cosð

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

x 1 1



as an equivalent form of

ðxÞ. This has the advantage of making the relationship

between the expressions deﬁning f and f

more clear. With this notation, some of

the limits that we learned in Section 3.1 can be expressed by formulas for the

derivatives of express ions. Thus (3.1.6) becomes

ðα  x

Þ5 α  nx

n21

for n 521; 0; 1; 2; 3: ð3:2:9Þ

Also, now that we are thinking of the derivative as a function, formulas in Section

3.1 that we stated for a ﬁxed argument c can be restated in terms of a variable

argument x. Thus if α and β are constants, then equations (3.1.7), (3.1.8), and

(3.1.9) become

ðα f Þ

ðxÞ5 α  f

ðxÞ; ð3:2:10Þ

ðf 1 gÞ

ðxÞ5 f

ðxÞ1 g

ðxÞ; ð3:2:11Þ

and, more generally,

ðα  f 1 β  gÞ

ðxÞ5 α  f

ðxÞ1 β  g

ðxÞ: ð3:2:12Þ

Summary of

Differentiation

Formulas

The differentiation formulas that appear in the following table are used frequently

and should be memorized. Several additional formulas will be added to the table in

later sections.

ðx

Þ 5 nx

n21

for n 521; 0; 1; 2; 3

sinðxÞ 5 cosðxÞ

cosðxÞ 52sinðxÞ

612345

0.5

1.0

1.0

0.5

cos(x)

x  0.00001

sin(x  x)  sin(x)

x

m Figure 9b

186 Chapter

3 The Derivative

QUICK QUIZ

1. Calculate

ð3 sinðxÞÞ:

2. Calculate





3. If f (x) 5 cos ðxÞ; then what is f

ðπ=3Þ?

4. What is the equation of the tangent line to the graph of

y 5 8 sinðxÞat ðπ=3; 4

ﬃﬃﬃ

Þ?

Answers

1. 3 cos (x)2

.21x

1 5=x

3. 2

ﬃﬃﬃ

=24.y 5 4ðx 2 π=3Þ1 4

ﬃﬃﬃ

EXERCISES

Problems for Practice

c In each of Exercises 110, compute the indicated deriva-

tive for the given function by using the formulas and rules

that are summarized at the end of this section. b

1. f

ð23Þ; fðxÞ5 sinðxÞ2 cos ðxÞ

gðπ=2Þ; gðtÞ5 t

=3 1 cosðtÞ

Þ; FðuÞ5 5u 1 6cosðuÞ

4. Dðf Þð0Þ; f ðxÞ523sinðxÞ

gð5Þ; gðtÞ5 8t

2 8t

6. DðHÞð1Þ; HðxÞ5 10=x

7. f

ðcÞ; f ðxÞ5 3sinðxÞ1 4cosðxÞ

dϕ

Þ; ϕðωÞ5 2 sinðωÞ1 5

s522

; gð s Þ5 3s

2 cosðsÞ

10.

x50

; f ðxÞ5 10x 2 3 sinðxÞ

c In Exercises 1114, calculate g

(x) by using the formulas

and rules that are summarized at the end of this section. b

11. gðxÞ52πx 1 1=ðπxÞ

12. gðxÞ5 x

2 4x

13. gðxÞ5 4x

1 6x

1 1

14. gðxÞ5 2x 1 sinðxÞ

c In each of Exercises 1518, ﬁnd a point x wh

ere f

(x) 5 6. b

15. f (x) 5 x

1 5

16. f (x) 5 12 sin (x)

17. f (x) 5 x

1 1

18. f (x) 5 3x

2 6x 1 50

c In each of Exercises 1922, calculate f

(x), and sketch the

graph of the equation y 5 f

(x). b

19. f ðxÞ5 3 2 2x

20. f ðxÞ5 x

1 3x

21. f ðxÞ5 x

1 jxj

22. f ðxÞ5 3x 2 jxj

c In each of Exercises 2326, a function f and

a value c are

given. Find an equation of the tangent line to the graph of f at

(c, f (c)). b

23. f ðxÞ5 sinðxÞ; c 5 π=3

24. f ðxÞ5 cosðxÞ; c 5 π=6

25. f ðxÞ5 2

cosðxÞ2 4sinðxÞ; c 5 3π=4

26. f ðxÞ5 3x 2 cosðxÞ; c 5 π=2

c In each of Exercises 2730, use the method of Example 1

calculate f

(x) for the given function f. b

27. f ðxÞ5

ﬃﬃ

ﬃ

28. f ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

x 1 3

29. f ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

3x 1 7

30. f ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

9 2 x

Further Theory and Practice

31. Figure 10 illustrates the graphs of four functions: F, G, H,

and K. Three of these functions are derivatives of the

others. Identify these relationships with equations of the

form g 5 f

where g and f are chosen from among F, G, H,

and K.

c In Exercises 3235, calculate the derivative of the given

function f at

the given point c. b

32. f (x) 5 jxj

3=2

; c 5 0

m Figure 10

3.2 The Derivative 187

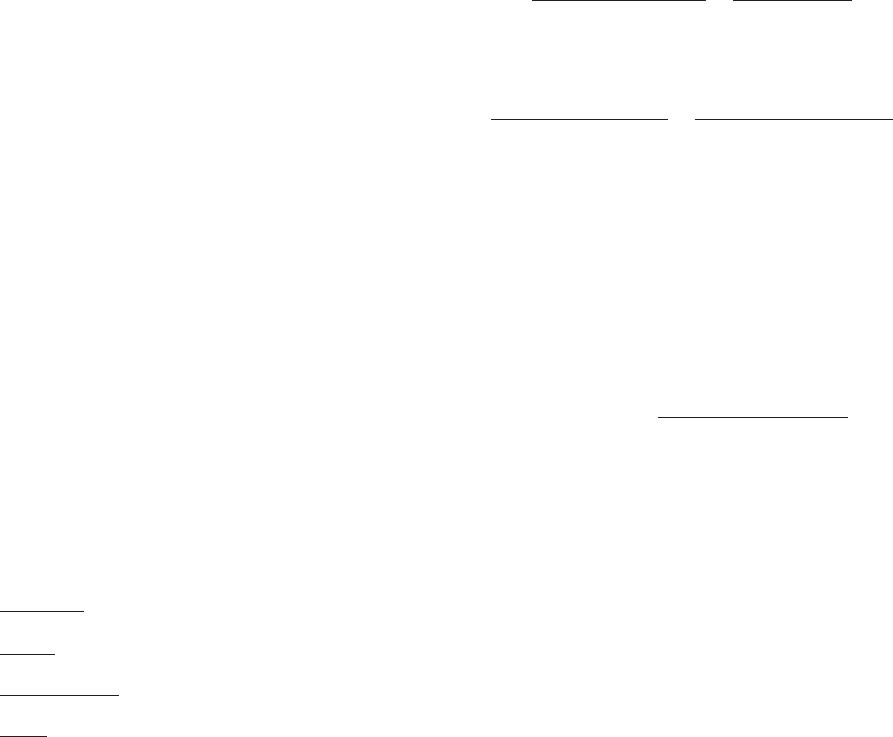
33. f (x) 5 x jxj; c 5 0

34. f (x) 5 x

3=2

; c 5 1

35. f (x) 5 1=

ﬃﬃﬃ

; c 5 1=16

36. Suppose that f ðxÞ5 jx 2 2j1 j x 2 3j: What is the domain

of f

? Sketch the graph of f

37. Find a polynomial function p(x) of degree 1 such that

p(2) 5 6 and p

(4)525.

38. Find a polynomial function of degree 2 such that p(3) 5 4,

p(5)5210, and p

(23) 5 7.

c In each of Exercises 3942 a function f is

given. Calculate

(x). b

39. f ðxÞ5 1=ð1 1 xÞ

40. f ðxÞ5 1=ð1 1 x

41. f ðxÞ5 1=ð1 1

ﬃﬃﬃ

42. f ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 x

c In each of Exercises 4346, a multicase function f is

deﬁned.

Is f differentiable at x 5 0? Give a reason for your

answer. b

43. f ðxÞ5

if x # 0

x if x . 0



44. gðxÞ5

if x # 0

if x . 0



45. f ðxÞ5

sinðxÞ if x # 0

1 x if x . 0



46. f ðxÞ5

sinðjxjÞ if x # 0

1 2 x if x . 0



c In Exercises 4750, specify a function f and

a value c for

which the given limit equals f

ðcÞ. (You need not evaluate the

limit.) b

47. lim

h-0

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

4 1 h

2 2

48. lim

h-0

2 1

49. lim

h-0

1=ð5 1 hÞ2 1=5

50. lim

h-0

sinðhÞ

51. An increasing, differentiable function may have a

decreasing derivative. That is, it may happen that f (a) ,

f (b)butf

(a) f

(b) for all a and b in the domain of f with

a , b.Showthatf ðxÞ5

ﬃﬃﬃ

has these properties.

52. If f (2x) 5 f (x) for every x, then f is said to be an even

function. If f (2x) 52f (x), for every x, then f is said to be

an odd function. Assume that f is differentiable. Show

that if f is even, then f

is odd. Show that if f is odd, then

is even.

53. Evaluate f

(0) if f (x) 5 x

where α $ 1. Show that f (x) 5

is not differentiable at 0 if α , 1.

54. Find a continuous function f on R that is differentiable on

(2N,0),(0,N) such that f (0) 5 0 and f

(x) 5 H(x) for

x 6¼0. Here H is the Heaviside function:

HðxÞ5

0ifx , 0

1ifx . 0



55. Let f ðxÞ5 x=ð1 1 x

Þ. Use the identity

x=ð1 1 x

Þ2 c=ð1 1 c

x 2 c

1 2 xc

ð1 1 x

Þð1 1 c

to compute f

ðcÞ.

56. Let f ðxÞ5 x=ð11x

: Use the identity

x=ð11x

2 c=ð 11c

x 2 c

1 2 cx

2 c

2 2xc 2 xc

ð11x

ð11c

to compute f

ðcÞ.

57. Suppose that f is differentiable at c. Let g (x) 5 f (x 1 k)

where K is a constant. Show that g is differentiable at

c2k, and evaluate g

(c2k) in terms of f

ðcÞ.

58. Suppose that f is a differentiable function and that K is a

constant. Deﬁne g (x) 5 f (kx). Show that g is differenti-

able, and ﬁnd a formula for g

(x) in terms of f

(kx).

59. In economics, if q(p) is the demand for a product at price

p; that is, the number of units of the product that are sold

at price P, then

EðpÞ52 lim

Δp-0

ðqðp 1 ΔpÞ2 qðpÞÞ=qðpÞ

Δp=p

is deﬁned to be the elasticity of demand. Compute E(p )in

terms of the derivative of the demand function q.

60. Let C(x) denote the cost of producing x units of a com-

modity. Although x usually refers to a nonnegative inte-

ger, it is common in economics to treat x as a continuous

variable. The marginal cost M(x) refers to the cost of

producing an x 1 1

unit after x units are produced.

a. Describe M in terms of C.

b. Write down the limit deﬁnition of C

(x). What is the

relationship between this quantity and M(x)?

c. Under what circumstances can we plausibly use C

(x)

as an expression for the marginal cost?

61. Let K and M be positive constants. Suppose that as popu-

lation P(t) increases from M/10 to M, it satisﬁes the equation

ðtÞ5 k  PðtÞðM 2 PðtÞÞ:

Show that the instantaneous rate of change of the

population is greatest when the population size is M/2.

62. Let the function f be speciﬁed by

f ðxÞ5

1 2ifx # 1

ax 1 b if x . 1:



Select a and b so that f

(1) exists.

63. Prove that the function

f ðxÞ5

x  sin ð1=xÞ if x 6¼ 0

0ifx 5 0



is continuous at x 5 0 but not differentiable at x 5 0.

188 Chapter 3 The Derivative

64. Prove that the function

f ðxÞ5

 sinð1=xÞ if x 6¼ 0

0ifx 5 0



is differentiable at x 5 0, and compute f

(0).

65. Let f be differentiable at c. Let y 5 ax1b be the equation

of the tangent line to the graph of f at ( c, f (c)). Prove that

lim

x-c

f ðxÞ2 ðax 1 bÞ

x 2 c

5 0:

Calculator/Computer Exercises

c In each of Exercises 6669, a function f, a viewing rec-

tangle R, and a point c are speciﬁed. Graph both f and the

tangent to the graph of f at (c, f (c)inR. b

66. f ðxÞ5

ﬃﬃ

ﬃ

; R 5 ½0; 43 ½0; 2; c 5 2

67. f ðxÞ5 x

2 2x; R 5 ½0; 13 ½21; 0; c 5 1=2

68. f ðxÞ5 sinðxÞ; R 5 ½0; π=23 ½0; 1; c 5 π=4

69. f ðxÞ5 1=x; R 5 ½1=2; 23 ½0; 2; c 5 1

c In each of Exercises 7073 a function f and

four values c,

, x

and x

are given. Using an appropriate viewing rec-

tangle centered about the point P 5 (c, f (c)), graph f and

the three secant lines passing through P that are determined

by (x

, f (x

)), (x

, f (x

)), and (x

, f (x

)). Use the secant line

through (x

, f (x

)) to estimate f

(c). b

70. f ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ﬃ

x 1 1

; c 5 0; x

5 0:5; x

5 0:3; x

5 0:1

71. f ðxÞ5 x=ðx 1 1Þ; c 5 1; x

5 1:8; x

5 1:5; x

5 1:2

72. f ðxÞ5 11 tanðxÞ; c 5 0; x

520:5; x

520:3; x

520:1

73. f ðxÞ5 sinðxÞ; c 5 π=4; x

5 1:2; x

5 1; x

5 0:8

c In Exercises 7477, approximate f

ðcÞ for the given f and c

in the following way: ﬁnd a small viewing window with P 5

(c, f (c)) near the center. The window should be small enough

so that the graph of f appears to be a straight line. Let Q and

R be the endpoints of the graph of f as it exits this window.

Use the slope of QR as the approximation to f

ðcÞ. b

74. f ðxÞ5 tan



sinðπ x=2Þ



; c 5 1

75. f ðxÞ5 ðx

1 x 1 1Þ=ðx

1 2Þ; c 5 1

76. f ðxÞ5 x 2 1=x; c 5 1

77. f ðxÞ5 cscðπxÞ; c 5 0:999

c In each of Exercises 7883,

a function f and a point c are

given. Graph the function

φðxÞ5

f ðxÞ2 f ðcÞ

x 2 c

in an appropriate viewing window centered about the line

x 5 c. Use the graph of φ to decide whether or not f

ðcÞ exists.

Explain the reason for your answer, and, if your answer is that

ðcÞ exists, use the graph of φ to approximate the value of

ðcÞ. b

78. f ðxÞ5 jxj; c 5 0

79. f ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ﬃ

2 3x 1 2

; c 5 1

80. f ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 2x

1 2x 2 1

; c 5 1

81. f ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

cosðxÞ

; c 5 π=2

82. f ðxÞ5

sin

ðxÞ=x if x 6¼ 0

0ifx 5 0

; c 5 0



83. f ðxÞ5

sinðxÞ=x if x 6¼ 0

1ifx 5 0

; c 5 0



c In Exercises 8487, graph the given function f in

the

suggested viewing rectangle R. From this graph, you will be

able to detect at least one point at which f may not be dif-

ferentiable. By zooming in, if necessary, identify each point c

for which f

ðcÞ does not exist. Sketch or print your ﬁnal graph,

and explain what feature of the graph indicates that f is not

differentiable at c. b

84. f ðxÞ5 x

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ﬃ

jcosðxÞj

; R 5 ½23; 33 ½23; 3

85. f ðxÞ5 cos

4=5

ðxÞ; R 5 ½0; 33 ½0; 1

86. f ðxÞ5 x sin

1=3

ðxÞ; R 5 ½1; 53 ½25; 2:5

87. f ðxÞ5

ﬃﬃﬃﬃﬃ

jxj

cos

1=3

ðx

Þ; R 5 ½21; 23 ½21:4; 1

88. Graph f ðxÞ52sinðxÞ and gðxÞ5 10

ðcosðx 1 :0001Þ2

cosðxÞÞ in the viewing rectangle ½0; 2π3 ½21; 1. What

differentiation formula does the graph illustrate?

89. Let f (x) 5 sin (2x). Graph

gðxÞ5 10



f ðx 1 10

Þ2 f ðxÞ



for 0 # x # π. Use your graph to identify f

(x).

3.3 Rules for Differentiation

In Sections 1 and 2, we learned how to differentiate some speciﬁc functions. For

example, we proved that if α is any real number, then

ðα  x

Þ5 α  nx

n21

for n 521; 0; 1; 2; 3:

3.3 Rules for Differentiation 189

The particular case in which n 5 0 is a rule that we use frequently: If f (x) 5 α for all

x, then f

(x) 5 0 for all x. In other words,

The derivative of a constant is zero.

We also derived the formulas

sinðxÞ5 cosðxÞ and

cosðxÞ52sinðxÞ:

However, if we want to know the derivative of other functions f, then, in general,

we must calculate

ðxÞ5 lim

Δx-0

f ðx 1 ΔxÞ2 f ðxÞ

Δx

This is the deﬁnition of the derivative, and all information about the derivative

follows from it. Working directly with this limit, however, can be difﬁcult or

tedious. It is therefore important to know some shortcuts, or rules, for calculating

derivatives. In this section, we will learn rules that tell us how to differentiate

algebraic combinations of basic functions.

Addition, Subtraction,

and Multiplication

by a Constant

In Section 3.1, we learned that ( f 1 g)

(x) 5 f

(x) 1 g

(x)and(f 2 g)

(x) 5 f

(x) 2

(x). We can state these differentiation rules as follows:

The derivative of a sum (or difference) is the sum (or difference) of the derivatives.

Moreover, if α is any constant, then (α f )

(x) 5 α f

(x). That is:

The derivative of a constant times a function is the constant times the derivative of the function.

Of course, we can also express these rules using Leibniz notation:

ðf 1 gÞðxÞ5

f ðxÞ1

gðxÞ;

ðf 2 gÞðxÞ5

f ðxÞ2

gðxÞ; and

ðα  f ÞðxÞ5 α 

f ðxÞ:

As we noted with formula (3.2.12), the last three equations can be combined into

one general form: If both α and β are constants, then (α f 1 β g)

(x) 5 α  f

(x) 1 β 

(x). A function of the form α f 1 β g is said to be a linear combination of f and

g. Using this terminology, the last derivative law may be stated as:

The derivative of a linear combination of functions is that linear combination of the derivatives of the functions.

As we observed in line (3.1.10), the rule for differentiating a linear combination can

be extended to three or more summands.

190 Chapter 3 The Derivative

⁄ EXAMPLE 1 Calculate

2 7x

1 2x 2 5 2



Solution We

reduce our differentia tion problem to simpler differentiations that

we already know. Thus



2 7x

1 2x 2 5 2



5 6

2 7

1 2

x 2

5 2 3

5 6  3x



2 7  2xðÞ1 2  1ðÞ2 0 2 3 





5 18x

2 14x 1 2 1

: ¥

Products and

Quotients

Now we turn to the differentiation of products and quotients. Because the deri-

vative of a sum and a difference both turned out to be easy and rather obvious, you

might assume that the derivative of a product or a quotient is equally simple. But

this is not so. For example, let f (x) 5 x

,andg(x) 5 x. Then we have

Derivative of Product

ðx

 xÞ5

ðx

Þ5 3x

Product of Derivatives

ðx

Þ

ðxÞ5 2x 1 5 2x:

Plainly the derivative of a product is not the product of the derivatives. Also

Dervative of Quotient Quotient of Derivatives





ðxÞ5 1

ðx

ðxÞ

5 2x:

So the derivative of a quotient is not the quotient of the derivatives.

The correct formulas are a bit surprising but not difﬁcult to use.

THEOREM 1

If f

ðcÞ and g

ðf  gÞ

ðcÞ¼f

ðcÞgðcÞ1 f

ðcÞg

ðcÞ:

Using Leibniz notation, the Product Rule is

ðf  gÞ5

 g 1 f 

In words, the Product Rule states:

We differentiate a product by adding the second function times the derivative of

the ﬁrst to the ﬁrst function times the derivative of the second.

A proof of the Product Rule may be found in the Genesis and Development

section at the end of this chapter. In the meantime, let us see how this rule is used.

3.3 Rules for Differentiation 191

⁄ EXAMPLE 2 Differentiate H(x) 5 x cos (x).

Solution We

think of H(x) as the product f (x) g(x), where f (x) 5 x and g(x) 5

cos (x). Therefore

ðxÞ 5 f

ðxÞgðxÞ1 f ðxÞg

ðxÞ





 cosðxÞ1 x 

cosðxÞ

5 1  cosðxÞ1 x ð2sinðxÞÞ

5 cosðxÞ2 xsinðxÞ: ¥

Sometimes it is necessary to differentiate a product of three (or more) func-

tions

. To treat such a problem, we apply the Product Rule successively. Here is

an example.

⁄ EX

AMPLE 3 Differentiate H(x) 5 x

sin (x)cos(x) with respect to x.

Solution We

think of H(x) as the product f (x) g(x), where f (x) 5 x

sin (x) and

g(x) 5 cos (x). A ﬁrst application of the Product Rule gives us

HðxÞ 5

ðf  gÞðxÞ

f ðxÞgðxÞ1 f ðxÞ

gðxÞ





sinðxÞ





 cosðxÞ1



sinðxÞ





cosðxÞ





sinðxÞ





 cosðxÞ1



sinðxÞ







2sinðxÞ







sinðxÞ





 cosðxÞ2 x

sin

ðxÞ:

To complete the differentiation, we apply the Product Rule one more time:

HðxÞ 5





sinðxÞ1 x

sinðxÞ

 cosðxÞ2 x

sin

ðxÞ



2xsinðxÞ1 x

cosðxÞ



 cosðxÞ2 x

sin

ðxÞ

5 2xsinðxÞcosðxÞ1 x

cos

ðxÞ2 x

sin

ðxÞ

5 2xsinðxÞcosðxÞ1 x



cos

ðxÞ2 sin

ðxÞ



: ¥

Now we will learn to differentiate the quotient f / g of

two functions. First we

will investigate the special case that is obtained by taking f (x) 5 1. It is useful, so

we record it separately:

THEOREM 2

The Reciprocal Rule If g

(c)

exists. Moreover,

192 Chapter 3 The Derivative





ðcÞ52

ðcÞ

Proof. We

start with the deﬁnition of (1/g)

(c):





ðcÞ

5 lim

Δx-0

1=gðc 1 Δx Þ2 1=gðcÞ

Δx

52lim

Δx-0

ðgðc 1 ΔxÞ2 gðcÞÞ

Δx  gðcÞgðc 1 ΔxÞ

52lim

Δx-0

ðgðc 1 Δ x Þ2 gðcÞÞ

Δx

 lim

Δx-0

gðcÞgðc 1 ΔxÞ

52g

ðcÞ

gðcÞ

’

⁄ EX

AMPLE 4 Show that

secðxÞ5 secðxÞtanðxÞ:

Solution Becau

se sec (x) 5 1/cos (x), the Reciprocal Rule ap plies:

secðxÞ 52

cosðxÞ

cos

ðxÞ

2sinx

cos

ðxÞ

sinx

cos

ðxÞ

cosðxÞ



sinðxÞ

cosðxÞ

5 secðxÞtanðxÞ:

This formula will be added to the list of basic derivatives that we are compiling.

THEOREM 3

The Quotient Rule: If f

ðcÞ and g

( f / g)



ðcÞ5

gðcÞf

ðcÞ2 f ðcÞg

ðcÞ

Proof. Notice

that the quotient f/g may be written as the product f (1/ g ).

The Reciprocal Rule tells us that (1/g)

( f (1/g))

3.3 Rules for Differentiation 193





ðcÞ5



f 





ðcÞ

5 f

ðcÞ





ðcÞ1 f ðcÞ





ðcÞ

5 f

ðcÞ



gðcÞ



1 f ðcÞ



ðcÞ



5 f

ðcÞ



gðcÞ

ðcÞ



1 f ðcÞ



ðcÞ



gðcÞf

ðcÞ2 f ðcÞg

ðcÞ

ðcombining term s; using common denominator g

ðcÞÞ: ’

⁄ EXAMPLE 5 Calculate the derivative of

HðxÞ5

1 1

Solution Observe

that H(x) 5 f (x)/g(x) where f (x) 5 x

1 1 and g(x) 5 x

. Then

ðxÞ 5

gðxÞf

ðxÞ2 f ðx Þg

ðxÞ

ðgðxÞÞ

ðx

Þð2 x Þ2 ðx

1 1Þð3x

ðx

2 3x

ðx

1 3Þ

Notice that this calculation makes sense only if g(x) 6¼0; that is, when x 6¼0.

Numeric Differentiation The rules that we have learned enable us to differentiate ex tremely complicated

functions. The application of these rules, however, can be laborious. Moreover,

even when we use a differentiation rule to obtain an exact evaluation of a deri-

vative, we may have to approximate consta nts such as

ﬃﬃﬃ

and π that appear in our

answer. It is therefore convenient to have a method for approximat ing the

numerical value f

ðcÞ right from the outset. Such a procedure is known as numeric

differentiation.

Suppose that f is a function that is deﬁned on the interval (a, b) and differ-

entiable at a point c in the interval. Because

ðcÞ5 lim

h-0

f ðc 1 hÞ2 f ðcÞ

;

we can approximate f

ðcÞ by the difference quotient (f (c 1 h) 2 f (c))/h for a small

value of h. When h . 0andc is ﬁxed, the quotient

f ðc; hÞ5

f ðc 1 hÞ2 f ðcÞ

194 Chapter 3 The Derivative