Blank L., Tarquin A. Engineering Economy (McGraw-Hill Series in Industrial Engineering and Management)
Подождите немного. Документ загружается.


,
SECTION 4.6 Equ
iv
alence Relations: Series w
ith
PP
2:
CP
Solution
Figure 4
-8
shows the cash
flow
diagram. Throughout the 20 semiannual periods, the an-
nu
al cost occurs every other period, and the capital recovery series
is
sought for every
6-month period. This pattern makes the solution by hand quite involved if
th
e P / F factor,
not the
P / A factor,
is
used to
find
P for the
10
annual $200,000 costs. The computer solu-
tion
is
recommended
in
cases such as this.
Solution
by hand- rate
I:
Steps to
find
the
semjarUJUal
A value are summarized below:
PP = CP at 6-months;
find
the effective rate per semiannual period.
Effective semiannual
i =
8%/2
= 4% per 6-months, compounded semiannually.
Number
of
semiannual periods n = 2(J 0) = 20.
Calculate P, using the P / F factor for n =
2,4,
...
, 20 periods since the costs are annual,
not semiannual. Then use
th
e
A/
P factor over 20 periods to
find
the semiannual A.
P = 3,000,000 + 200,000
[
k~4
(P /
F,4%,k)]
= 3,000,000 + 200,000(6.6620) = $4,332,400
A = $4,332,400(A / P,4%,20) = $318,778
Conclusion: Reve
nu
e
of
$3
18
,778
is
nec
essa
ry
every 6 months to cover all costs and inter-
est at 8% per year, compounded semiannually.
Solution
by
hand-rat
e 2: The PP is se
mi
annual, bot the CP is now monthl
y;
therefore,
PP >
CP.
To
find
th
e effec
ti
ve semiannual rate, the effective interest rate, Equation [4.8], is
applied with
r = 4% and
In
= 6 months per semiannual period.
Effective semiannual
i =
(I
+
0.~4r
- I = 4.067%
P = 3,000,000 + 200,000
[k
~4
(P / F,4.067%,k)]
= 3,000,000 + 200,000(6.6204) = $4,324,080
A = $4,324,080
(A/
P
,4
.067%,20) = $320,064
A per 6 months = ?
0
2
4
6
8
10
12
J4
16
18
20
6 months
I 2
3
4
5 6
7
8
9
10
Years
$200,000 p
er
year
i
l
= 8%,
compo
unded semiannua
ll
y
i2 = 8%,
compo
unded monthly
P = $3 million
Figure
4-8
Cash flow
diagram with
two different
compounding
periods,
Example 4.9.
145

146
CHAPTER 4 Nominal and Effective Interest Rates
Now, $320,064, or $1286 more semiannually,
is
required to cover the more frequent com-
pounding
of
the 8% per year interest. Note that all PI F and AI P factors must be calculated
with factor formulas at 4.067%. This method
is
usually more calculation-intensive and
error-prone than with a spreadsheet solution.
Solution by
computer-rates
1 and 2: Figure
4-9
presents a general solution for the prob-
lem
at both rates. (Several rows at the bottom
of
the spreadsheet are not printed. They
continue the cash flow pattern
of
$200,000 every other 6 months through cell B32.)
The
functions
in
C8 and
E8
are general expressions for the effective rate per PP, expressed
in
months. This allows some sensitivity analysis to be performed for different PP and
CP
values. Note the function
in
C7 and E7 to determine m for the effective rate relations. This
technique works well for spreadsheets once
PP and CP are entered
in
the time unit
of
the
CP.
Each 6-month period
is
included
in
the cash flows, including the $0 entrie
s,
so the NPV
a
nd
PMT functions work con·ectly. The final A values
in
014
($318,784) and F14
($320,069) are the same (except for rounding)
as
those above.
X I.hcrosoft
Excel·
Example 4.9
I!lIiIEf
Semiannual
period
o
1
2
3
Figure 4- 9
0 E
8%
8~~
Semiannual Month
20 20
----sill
6 6
6
1
~
=
ES
/
E6
1
1 6
4.00% 4.07%
= +
«(1
+
«E2/(12/ES
))/E7
))A
E7
)-
1
Cash
fi
ow
= N
PV
(E
S,
8 13
:8
32)+ B
12
$3,000,000
Prese
nt
worth
$4.
332,385
$
A, $!l3·month $ 318,784
$
200 ,000 L:...:!...:;;;:....;;.;.:c.:..:.;..c---'---':..:.:::;.,.:...::...;-L-
____
~==::....r
$
$ 200,000
$
$
=
PMT
(
ES
,E4
,-
FI2
)
I
~~=~~~o;--.,.,-J
I
.l..
1
,
Nur
Vl
,
Spreadsheet solution for semiannual A series for different
compounding
periods,
Ex
ample 4.9.

SECTION 4.7
Equivalence
Relation·
,:
Single Amounts and Series With
PP
<
CP
4.7 EQUIVALENCE RELATIONS: SINGLE
AMOUNTS
AND
SERIES
WITH
PP
<
CP
If
a person deposits money each month into a savings account where interest is
compounded quarterly, do all the monthly deposits earn interest before the next
quarterly compounding time?
If
a person's credit card payment
is
due with inter-
est
on
the 15th
of
the month, and if the full payment is made on the 1 st, does the
financial institution reduce the interest owed, based on early payment?
The
usual
answers are 'No'. However, if a monthly payment on a
$10 million, quarterly-
compounded, bank loan were made early by a large corporation, the corporate
financial officer would likely insist that the bank reduce the amount
of
interest
due, based on early payment. These are examples
of
PP
<
CP.
The
timing
of
cash flow transactions between compounding points introduces the question
of
how interperiod compounding
is
handled. Fundamentally, there are two policies:
interperiod cash flows earn
no interest, or they earn compound interest.
For a no-interperiod-interest policy, deposits (negative cash flows) are all re-
garded
as
deposited at the end
of
the compounding period, and withdrawals are
all regarded as
withdrawn at the beginning. As an illustration, when interest is
compounded quarterly, all monthly deposits are moved to the end
of
the quarter
(no interperiod interest
is
earned), and all withdrawals are moved to the begin-
ning (no interest
is
paid for the entire quarter). This procedure can significantly
alter the distribution
of
cash flows before the effective quarterly rate is applied to
find
P, F, or A. This effectively forces the cash flows into a
PP
=
CP
situation, as
discussed in Sections 4.5 and 4.6. Example
4.10 illustrates this procedure and the
economic fact that, within a one-compounding-period time frame, there is no
interest advantage to making payments early.
Of
course, non-economic factors
may be present.
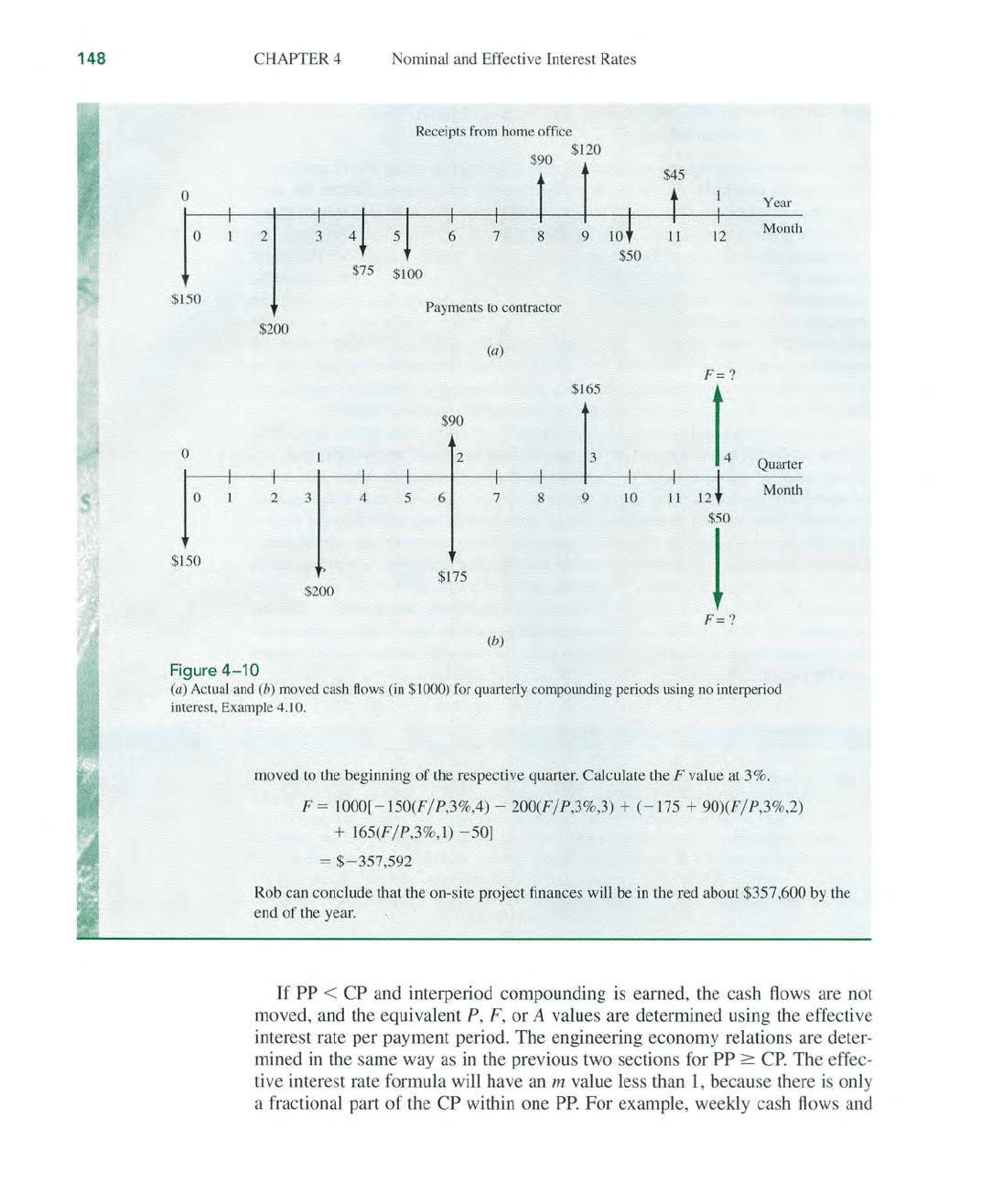
EXAMPLE 4.10
.~.
Rob is the on-site coordinating engineer for Alcoa Aluminum, where an under-renovation
mine has new
ore
refining equipment being installed by a local contractor.
Rob
developed
the cash flow diagram
in
Figure 4-
IOa
in
$1000 units from the project perspective. In-
cluded are payments to the contractor he has authorized for the current year and approved
advances
fi
·om Alcoa's home office.
He
knows that the interest rate on equipment "field
projects"
such as this
is
12% per year, compounded quarterly, and that Alcoa does not
bother with interperiod compounding
of
interest. Will Rob's project finances be in the
"red"
or
the "black" at the end
of
the year? By how
much?
Solution
With no interperiod interest considered, Figure
4-10b
reflects the moved cash flows.
The
future worth afler four quarters requires an F at an effective rate per quarter
of
12
%/
4 = 3%. Figure 4- 1
Ob
shows all negative cash flows (payments to contractor)
moved
to the end
of
the respective quarter, and
aU
positive cash flows (receipts from home office)
147
148
CHAPTER 4 Nominal and Effective Interest Rates
Receipts from home office
$
90
$120
0
Year
0
2 3
4
6 7
12
Month
$75
$100
$
150
Payments to contractor
$200
(a)
F=
?
$165
$90
0
2 3
t
Quarter
0
2
3
4
5 6 7 8 9
10
11
J2t
Month
$50
$150
r>
$175
$
200
l
F=
?
(b)
Figure
4-10
(a) Actual and (b) moved cash
Aows
(in
$1000)
for quarterly compounding periods using
no
interperiod
interest, Example 4. J
O.
moved
to
the beginning
of
the respective quarter. Calculate the F value at 3
0/0
.
F = 1000[ -
150(F/P
,3
0/0,
4) -
200(F/
P,3%,3) + (- 175 +
90)(F
/ P,3%,2)
+ 165(F/ P,3%
.l)
- 50]
= $- 357,592
Rob can conclude that the on-site project finances will be
in
the red about $357,600 by the
end
of
the year.
If
PP < CP and interperiod compounding
is
earned, the cash flows are not
moved, and the equivalent
P,
F,
or A values are determined using the effective
interest rate per payment period. The engineering economy relations are deter-
mined in the same way as in the previous two sections for
PP
;:::
CP.
The effec-
tive interest rate formula will have an
m value less than 1, because there is only
a fractional part
of
the
CP
within one
PP.
For
example, weekly cash flows and

SECTION
4.
8 Effective Interest Rate for Continuous Compounding
quarterly compounding require that m =
1/13
of
a quarter.
When
the nominal
rate is 12% per year, compounded quarterly (the
same
as
3%
per quarter, com-
pounded quarterly), the effective rate
per
PP
is
Effective weekly i%
= (1.03)1/13 - 1 = 0.228% per week
4.8
EFFECTIVE INTEREST
RATE
FOR CONTINUOUS
COMPOUNDING
If
we allow compounding to occur more and more frequently, the compounding
period becomes shorter and shorter. Then
m,
the number
of
compounding peri-
ods per payment period, increases. This situation occurs in businesses that have
a very large number
of
cash flows every day, so it is correct to consider interest
as compounded continuous
ly.
As m approaches infinity, the effective interest
rate, Equation
[4.8], must be written in a new form. First, recall the definition
of
the natural logarithm base.
lim 1 +
- = e =
2.71828+
(
1)
11
,,
-'>00
h
[4.11]
The limit
of
Equation [4.8] as m approaches infinity is found by using
r/m
=
l/h
, which makes m = hr.
r)1II
+ -
-1
m
(
1)'11
.
=
Ii
m I + - - 1
Ii
-,>
oo
h
[(
1)"Jr
= lim 1 + - - 1
11.
-'>
00
h
[4.12]
Equation [4.12] is used to compute the effective continuous interest rate, when
the time periods on
i and r are the same. As an illustration,
if
the nominal annual
r =
15
% per year, the effective continuous rate per year is
i%
=
eO.
ls
-
1 = 16.183%
For
convenience, Table
4-3
includes effective continuous rates for the nominal
rates listed.
EXAMPLE 4.11
ff~
(a) For
an
interest rate
of
18% per year, compounded continuously, calculate the ef-
fective monthly and annual interest rates.
(b)
An
investor requires an effective return
of
at least
15
%. What
is
the minimum
annual nominal rate that is acceptable for continuous compounding?
149

150
CHAPTER 4
Nominal and Effective Interest Rates
Solution
(a)
The
nominal monthly rate is r =
18
%/
12 = 1.5%,
or
0.015 per month. By
Equation [4.12], the effective monthly rate is
i% per month
= e
r
- 1 =
eo.O
JS
- 1 = 1.511%
Similarly, the effective annual rate using
r = 0.18 per year is
i% per year
= e
r
- 1 =
eO
ls
- 1 = 19.72%
(b) Solve Equation [4.12] for r by taking the natural
lo
garithm.
e'
- 1 = 0.15
e'
= 1.15
In
e'
=
In
1.15
r% = 13.976%
Therefore, a rate
of
13.976% per year, compounded continuousl
y,
will generate
an effective
15
% per year return.
Comment
The
general fon";ula to find the nominal rate, given the effective continuous rate i, is
r =
In
(1
+ i)
EXAMPLE
4.12
'.
Engineers Marci and Suzanne both invest $5000 for
10
years at 10%
per
yea
r.
Compute
the future worth for both individuals
if
Marci re
ce
ives annual compounding a
nd
Su
za
nne receives continuous compounding.
Solution
Marci: For annual compounding tbe future worth is
F = P
(F/
P,1O
%,lO) = 5000(2.5937) = $12,969
Su
za
nne: Using Equation
[4
.12], first find the effective i per year for use
in
the F / P
factor.
Effective i%
=
eO
J
O - 1 = 10.517%
F =
P(F
/ P,
1O
.517%,
10)
= 5000(2.7183) = $13,
591
Continuous compounding causes a $622 increase
in
earnings. For comparison, daily
compounding yields an
ef
fective rate
of
10.516%
(F
= $13,590), only slightly less than
the I 0.517% for continuous compounding.

SECTION 4.9 Interest Rates That Vary Over Time
For some business activities, cash flows occur throughout the day. Examples
of
costs are energy and water costs, inventory costs, and labor costs. A realistic
model for these activities is to increase the frequency
of
the cash flows to become
continuous. In these cases, the economic analysis can be performed for continu-
ous cash flow (also called continuous
fuRds flow) and the continuous com-
pounding
of
interest as discussed above. Different expressions must be derived
for the factors for these cases. In fact, the monetary differences for continuous
cash flows relative
to
the discrete cash flow and discrete compounding assump-
tions are usually not large. Accordingly, most engineering economy studies do
not require the analyst to utilize these mathematical forms to make a sound eco-
nomic project evaluation and decision.
4.9 INTEREST
RATES
THAT VARY OVER TIME
Real-world interest rates for a corporation vary from year to year, depending upon
the financial health
of
the corporation, its market sector, the national and interna-
tional economies, forces
of
inflation, and many other elements. Loan rates may
increase from one year to another. Home mortgages financed using
ARM
(ad-
justable rate mortgage) interest is a good example.
The
mortgage rate is sljghtly
adjusted annually to reflect the age
of
the loan, the current cost
of
mortgage
money, etc. An example
of
interest rates that rise over time is inflation-protected
bonds that are issued by the U.S. government and other agencies.
The
dividend
rate that the bond pays remains constant over its stated life, but the lump-sum
amount due to the owner when the bond reaches maturity
is
adjusted upward with
the inflation index
of
the Consumer Price Index (CPI). This means the annual rate
of
return will increase annually in accordance with observed inflation. (Bonds and
inflation are visited again
in
Chapters 5 and 14, respectively.)
When
P, F, and A values are calculated using a constant
or
average interest rate
over the life
of
a project, rises and falls in i are neglected.
If
the variation
in
i is
large, the equivalent values will vary considerably from those calculated using
the constant rate. Although an engineering economy study can accommodate
varying
i values mathematically, it
is
more involved computationally to do so.
To determine the
P value for future cash flow values
(F)
at different i values
(i/) for each year t, we will assume annual compounding. Define
i/
= effective annual interest rate for year t
(t
= years 1 to n)
To
determine the present worth, calculate the P
of
each
F/
value, using the applic-
able
i
f'
and sum the results. Using standard notation and the P / F factor,
P =
FI(P
/
F,il,l)
+
FlP
/ F,i
l
,
1)(P/F,i2,l)
+
...
+ F
n
(P/F,i
l
,l)(P/F,i2,l)
...
(P/F,in,l)
[4.13]
When only single amounts are involved, that is, one P and one F in the final year
n, the last term
in
Equation [4.13]
is
the expression for the present worth
of
the
future cash flow.
P = F
II
(P
/
F,i
1
,1)(P/
F,i
2
,1)'"
(P/
F,i
ll
,l)
[4.14]
151

152
EXAMPLE 4.13
o
1
i=
7o/J
p=
?
Figure
4-11
CHAPTER 4 Nominal and Effective Interest Rates
If
the equivalent uniform series A over all n years
is
needed, first find P using ei-
ther
of
the last two equations, then substitute the symbol A for each
F,
symbol.
Since the equivalent
P has been determined numerically using the varying rates,
this new equation will have only one unknown, namely,
A. The following exam-
ple illustrates this procedure.
CE, Inc., leases large earth tunneling equipment. The net profit from the equipment for
each
of
the last 4 years has been decreasing, as shown below. Also shown are the annual
rates
of
return on invested capital. The return has been increasing. Determine the present
worth
P and equivalent uniform series A
of
the net profit series. Take the annual variation
of
rates
of
return into account.
Year
Net
Profit
Annual Rate
Solution
1
$70,000
7%
2
$70,000
7%
3
$35,000
9%
4
$25,000
10
%
Figure
4-11 shows the cash flows, rates for each year, and the equivalent P and A. Equa-
tion [4.13]
is
used to calculate
P.
Since for both years 1 and 2 the net profit is $70,000 and
the annual r,ate
is
7%, the P / A factor can be used for these 2 years only.
$70,000
2
i=7
%
$35,000
3
i=9
%
P = [70(P/A,7%,2) +
35(P/F,7%,2)(P/F,9%,l)
+ 25(P/F,7%,2)(P/ F,9
%,
1)(P/
F,
10%,1)](1000)
= [70(1.8080) + 35(0.8013) + 25(0.7284)](1000)
= $172,816
A
=?
$25,
4 2
7% 7% 9%
i=
10%
$172,816
[4.15]
3
4
10%
Eq
uivalent P and A values for varying interest rates, Example 4.13.

CHAPTER SUMMARY
To
determine
an
equivalent annual series, substitute the symbol A for all net profit values
on
the right side
of
Equation [4.15], set it equal to P = $172,816 and solve for
A.
This equa-
tion accounts for the varying
i values each year. See Figure 4-11 for the cash flow diagram
transformation.
$172,816
= A[(1.8080) +
(0
.8013) + (0.7284)] = A [3.3377]
A
=
$51
,777 per year
Comment
If
the average
of
the four annual rates, that is, 8.25
%,
is
used, the result
is
A = $52,467.
This
is
a $690 per year overestimate
of
the required equivalent amount.
When there
is
a cash flow in year 0 and interest rates vary annually, this cash
flow must be included when one
is
determining
P.
In the computation for the
equivalent uniform series
A over all years, including year 0, it
is
important to in-
clude this initial cash flow at
t = O. This is accomplished by inserting the factor
value for
(P
/
F,i
o,
O)
into the relation for A. This factor value is always 1.00.
It
is
equally correct to find the
A value using a future worth relation for F in year
n.
In
this case, the A value is determined using the F / P factor, and the cash flow in
year
n is accounted for by including the factor
(F
/ P,i",O) = 1.00.
CHAPTER SUMMARY
Since many real-world situations involve cash flow frequencies and compound-
ing periods other than 1 year, it is necessary to use nominal and effective interest
rates. When a nomjnal rate
r
is
stated, the effective interest rate per payment
period is determjned
by
using the effective interest rate equation.
(
~
\m
Effective i = 1 + (
iii')
- 1
The m is the number
of
compounding periods (CP) per payment period (PP).
If
interest compounding becomes more and more frequent, the length
of
a
CP
ap-
proaches zero, continuous compounding results, and the effective
i
is
e
r
-1.
All
engineering eco
nom
y factors require the use
of
an
effective interest rat
e.
The i and n values placed in a factor depend upon the type
of
cash flow series.
If
only single amounts (P and
F)
are present, there are several ways to perform
equivalence calculations using the factors. However, when series cash flows
(A, G, and g) are present, only one combination
of
the effective rate i and num-
ber
of
periods n is correct for the factors. This requires that the relative lengths
of
PP and
CP
be considered
as
i and n are determined. The interest rate
and
payment
periods
must
ha
ve the
sam
e time unit for the factors to correctly account for the
time value
of
money.
153

154
CHAPTER 4 Nominal and Effective Interest Rates
From
one
year
(or
interest period) to the next, interest rates will vary. To ac-
curately
perform
equivalence
calculations for P
and
A
when
rates vary signifi-
cantly, the
applicable
interest rate
should
be
used, not
an
average
or
constant
rate
.
Whether
performed
by
hand
or
by
computer
,
the
procedures
and factors
are
the
same
as those for
constant
interest rates;
however
,
the
number
of
calculations
increases.
PROBLEMS
Nominal and Effective Rates
4. 1 Identify
the
compounding
period
for
the
following
interest statements: (a) 1 %
per
month; (b) 2.5%
per
quarter; and (c) 9.3%
per
year
compounded
semiannually.
4.2
Identify the
compounding
period for
the
following interest statements: (a)
Nominal
7% per
year
compounded
quarterly;
(b) effective 6.8%
per
year
compounded
monthly; and (c) effective
3.4
%
per
quar-
ter
compounded
weekly.
4.3
Determine
the
number
of
times interest
would
be
compounded
in 1
year
for the
following intere
st
statements: (a) 1 %
per
month; (b) 2%
per
quarter; and (c) 8%
per
year
compounded
sem
iannually.
4.4
For
an interest rate
of
10%
per
year
com-
pounded
quarterly,
determine
the
number
of
times interest would
be
compounded
(a)
per
quarter
, (b)
per
year, and (c)
per
3 years.
4.5
For
an interest rate
of
0.50%
per
quarter
,
determine
the nominal interest rate
per
(a)
semiann
ual period, (b) year,
and
(c) 2 years.
4.6
For
an interest rate
of
12%
per
year
com-
pounded
every
2
months
,
determine
the
nominal interest rate
per
(a) 4
months
,
(b) 6
months
, and (c) 2 years.
4.7
For
an interest rate
of
10%
per
year,
com-
pounded
quarterly,
determine
the nominal
rate
per
(a) 6
months
and
(b) 2 years.
4.8 Identify the following interest rate state-
ments as either nominal
or
effective:
(a) 1.3%
per
month; (b) 1 %
per
week
,
com-
pounded weekly; (c) nominal
15
%
per
year,
compounded
monthly;
(d)
effective 1.5%
per month,
compounded
daily; and
(e)
15
%
per year,
compounded
semiannually.
4.9
What
effective
interest rate
per
6
months
is
equivalent
to 14%
per
year,
compounded
semiannually?
4.10
An
interest rate
of
16%
per
year,
com-
pounded
quarterly, is
equivalent
to
what
effective interest
rate
per
year?
4.
11
What
nominal interest rate
per
year
is
equivalent
to an effective 16%
per
year
,
compounded
semiannually?
4.12
What
effective interest
rate
per
year is
equivalent
to an effective 18% per year,
compounded
semiannually?
4.13
What
compounding
period is associated
with nominal
and
effective
rates
of
18%
and
18.81 %
per
year,
respectively?
4.14
An
interest
rate
of
1%
per
month
is
equivalent
to
what
effective
rate
per
2
months?
