Blank L., Tarquin A. Engineering Economy (McGraw-Hill Series in Industrial Engineering and Management)
Подождите немного. Документ загружается.


SECTION 7
.2
Rate
of
Return Calculation Using a PW or
AW
Equation
rate at which the PI
F,
PiA,
or
AI F value
is
satisfied.
The
rate obtained is a
good estimate for the first trial.
It
is important to recognize that this first-trial rate is only an estimate
of
the ac-
tual rate
of
return, because the time value
of
money is neglected.
The
procedure
is illustrated
in
Example 7.2.
i*
by
Computer
The
fastest way to determine an i* value by computer, when
there
is
a series
of
equal cash flows (A series),
is
to apply the RATE function.
This
is
a powerful one-cell function, where
it
is
acceptable to have a separate P
value
in
year 0 and an F value
in
year
n.
The
format is
R
ATE(n
,
A,
P
,F)
The
F value does not include the series A amount.
When
cash flows vary
from
year to year (period to period), the best way to
find
i*
is
to enter the net cash flows into contiguous cells (including any
$0
amounts) and apply the IRR function in any cell.
The
format is
IRR
(fir
sC
cell:l
asC
cell,guess)
where
"g
uess" is the i va
lu
e at which the
computer
starts searching for i*.
The
PW-based procedure for sensitivity analysis and a graphical estimation
of
the i* value (or multiple
i*
values, as discussed later) is as follows:
1.
Draw the cash flow diagram.
2. Set up the
ROR
relation
in
the form
of
Equation [7.1].
3. Enter the cash flows onto the spreadsheet
in
contiguous cells.
4. Develop the IRR function to display i
*.
5. Use the NPY function to develop a chart
of
PW
vs. i values. This graphi-
cally shows the i* value at which
PW
=
O.
The HVAC engineer for a company constructing one
of
the world's tallest buildings
(Shanghai Financial Center
in
the Peoples' Republic
of
China) has requested that $500,000
be spent now during const.ruction on software and hardware to improve the efficiency
of
the environmental control systems. This is expected to save $10,000 per year for
10
years
in
energy costs and $700,000 at the end
of
10
years in equipment refurbishment costs. Find
the rate
of
return by hand and by computer.
Solution
by
Hand
Use the trial-and-error procedure ba
se
d on a
PW
equation.
I. Figure 7- 3 shows the cash flow diagram.
2.
Use Equation [7.1] format for the
ROR
equation.
0 = - 500,000 +
10
,
000(P/A,i*,10)
+
700,000(P/F,i*,10)
[7.5]
245
Q-Solv
~
E-Solve

246
CH
APTER
7 Rate
of
Return Analysi
s:
Single
Alternative
i = ?
$700,000
I
$10,000
o
2
3 4 5
6
7
8 9 10
$500,000
Figure
7-3
Cash now diagram, Example 7.2.
3. U
se
the estimation
procedure
to determine i for the first trial. A
ll
income will be re-
garded as a single
F
in
year
10 so that the
PI
F factor can be used. The
PI
F factor
is
selected be
ca
use
most
of
the cash flow ($700,000) already fits this factor and errors
cr
ea
ted by neglecting the time value
of
the remaining money will
be
minimized.
Only for
th
e first estimate
of
i, define P = $500,000,11 = 10, and F = 10(10,000) +
700
,
000
= $8
00
,000.
Now
we
ca
n state that
500,000 = 800,000(P I F,i, I 0)
(PIF,i,1O) = 0.625
The
roug
hl
y estimated i is between 4% and 5%.
Use
5% as the first trial because this
approximate rate for the
PIF factor is lower than the true value when the time value
of
money
is
considered.
At
i = 5%, the
ROR
equation is
o = -
500
,0
00
+
LO
,O
OO
(P I A,5%, 10) + 700,000(P I F,5%, 1 0)
o < $
6946
The
result
is
positive, indicating that the return is more than 5%. Try i =
6%
.
o = -
500
,
000
+ I O,
OOO
(P I A,6
%,
10) + 700,000(P I
F,6%
, 10)
0 >
$-35,
519
Since the
int
erest rate
of
6% is too high, linearly interpolate between 5% and 6
%.
i* =
5.00
+ 6946 - 0 ( 1.0)
6946 -
(-3
5,519)
= 5.00 + 0.16 =
5.16
%

SECTION 7.2 Rate
of
Return Calculation Using a PW or
AW
Equation
Solution by
Computer
~
~
Enter the cash flows from Figure
7-3
into the RATE function. The entry RATE(
10
, 10000,
~
- 500000, 700000) displays
i*
= 5.16
%.
It
is
equally correct to use the
IRR
function.
Figure
7-4,
column B, shows the cash flows and IRR(B2:B
12)
function to obtain i*. Q-Solv
$54
,00
4
$44,2
04
$34,603
$25,
198
$15,984
$6,
957
1
-$1,888
-$10,555
$60,000
Q)
$40,000
.2
~
$20,000
~
$0
-$20,000
-$19,047 -$40 ,000
+-----,---,---,---,----,~
-$2
7,
368 3.
8%
4.2%
4.
6%
5.
0%
5.
4%
5.
8%
-$35,523
Interest rate i
'\
16
\..;....
0
,)10
----f":
"fRR('i32:E
~~~~~
\.
- =
NPV(Cl2,$B$3:$B$12)+$B$2
rRR(B2:B
12)
1
Ready
r [
NUIvl
Figure
7-4
Spreadsheet solution for
i*
and a plot
of
PW vs. i values, Example 7.2.
For a more thorough ana
ly
sis, use the i* by computer procedure above.
1,2.
The cash flow diagram and ROR relation are the same as
in
the by-hand solution.
3.
Figure 7- 4 shows the net cash flows
in
column
B.
4. The IRR function
in
ce
ll
BI4dispJays
r:'
= 5.16%.
5.
In
order
to
graphically observe
i*
, column 0 displays
PW
for different i values (col-
umn C). The NPV function
is
used repeatedly
to
calculate
PW
for the Excel
xy
scat-
ter chart
of
PW vs.
i.
The
i*
is
sl
ightly less than 5.2
%.
As indicated
in
the cell
012
tag, $ signs are inserted into the NPV functions. This provides
absolute cell referellcin
g,
which allows the NPV function to be correctly shifted from one
cell to another (dragged with the mouse).
~
E-Solve
247

248
~
E-Solve
CHAPTER 7
Rate
of
Return Analysis: Sing
le
Alternative
Just as
i*
can be found using a
PW
equation, it may equivalently be determined
using an A W relation. This method
is
preferred when uniform annual cash flows
are involved. Solution by hand is the same as the procedure for a
PW-based
relation, except Equation
[7
.
2]
is used.
The
procedure for solution by computer
is
exactly the same
as
outlined above
using the
IRR
function. Internally, IRR calculates the NPV function at different
i values until
NPV
= 0
is
obtained. (There
is
no equivalent way to utilize the
PMT
function, since it requires a fixed value
of
i to calculate an A value.)
EXAMPLE
7.3
Use
AW
computations to find the rate
of
return for the cash flows
in
Example 7.2.
Solution
I. Figure 7- 3 shows the cash flow diagram.
2. The AW relations for disbursements and receipts are formulated
USing
Equa-
tion [7.2].
AW
D
=
-500
,000(A/P,i,lO)
AW
R
=
10
,000 + 700,000(A/ F,i,lO)
0=
-500,000(A/P,i*,10) + 10,000 + 700,000(A/
F,i
*,10)
3. Trial-and-error solution yields these results:
At i
= 5%, 0 < $900
At i = 6
%,
0 >
$-4826
By interpolation, i* = 5.16%, as before.
In closing, to determine
i*
by hand, choose the PW, AW, or any other equiva-
lence equation. It is generally better to consistently use
one
of
the methods in
order to avoid errors.
7.3
CAUTIONS WHEN USING THE
ROR
METHOD
The
rate
of
return method is commonly used in engineering and business settings
to evaluate one project, as discussed in this chapter, and to select one alternative
from two or more, as explained in the next chapter.
When applied correctly, the
ROR
technique will always result in a good
decision, indeed, the same one as with a
PW
or
A W (or
FW)
analysis.
However, there are some assumptions and difficulties with
ROR
analysis that
must be considered when calculating
i*
and
in
interpreting its real-world mean-
ing for a particular project.
The
summary provided below applies for solutions
by hand and by computer.
• Multiple i* values. Depending upon the sequence
of
net cash flow disburse-
ments and receipts, there may be more than one real-number root to the
ROR
equation, resulting
in
more than one
i*
value. This difficulty is discussed in
the next section.

SECTION 7.4
MUltiple
Rate
of
Return
Values
• Reinvestment at i
*.
Both
the
PW
and A W methods assume that any net posi-
tive investment (i.e., net positive cash flows once the time value
of
money is
considered) are reinvested at the MARR. But the
ROR
method assumes rein-
vestment at the
i*
rate.
When
i*
is not close to the
MARR
(e.g.,
if
i*
is sub-
stantially larger than
MARR),
this is an unrealistic assumption. In such cases,
the
i* value
is
not a good basis for decision making. Though more involved
computationally than
PW
or
A W at the MARR, there is a procedure to use the
ROR
method and still obtain one unjque i* value.
The
concept
of
net positive
investment and this method are discussed in Section
7.5.
• Computational difficulty versus understanding. Especially in obtaining a
trial-and-error solution by hand for one
or
multiple
i*
values, the computa-
tions rapidly become very involved. Spreadsheet solution is easier; however,
there are no spreadsheet functions that offer the same level
of
understanding
to the learner as that provided by hand solution
of
PW
and AW relations.
• Special procedurefor multiple alternatives. To correctly use the
ROR
method
to choose from two
or
more mutually exclusive alternatives requires an analy-
sis procedure significantly different from that used in
PW
and
AW.
Chapter 8
explains this procedure.
In conclusion, from an engineering economic study perspective, the annual
worth
or
present worth method at a stated
MARR
should be used
in
lieu
of
the
ROR method. However, there
is
a strong appeal for the
ROR
method because
rate
of
return values are very commonly quoted. And it is easy to compare a pro-
posed project's return with that
of
in-place projects.
When working with two
or
more alternatives,
and
when it is
important
to
know the exact value
of
i*, a good
approach
is to determine
PW
or
A W
at
~::~:i;~
~;;~:~~~;~;'::~;;~;;;~:~~~::;;:~~:;i;:;~;:,~~a;~~
\
\
~~lculate
the exact
i*
and report it along with the conclusion that the project is
financially justified.
7.4 MULTIPLE
RATE
OF
RETURN VALUES
In Section 7.2 a unique rate
of
return
i*
was determined. In the cash flow series
presented thus far, the algebraic signs on the
net cashjlows changed only once,
usually from minus
in
year 0 to plus at some time during the series. This is called
a
conventional (or simple) cash jlow series. However, for many series the net
cash flows switch between positive and negative from one year to another, so
there is more than one sign change. Such a series is called
nonconventional (non-
simple).
As shown in the examples
of
Table
7-3,
each series
of
positive
or
nega-
tive signs may be one
or
more
in
length. When there is more than
one
sign
change
in
the net cash flows, it
is
possible that there will be multiple
i*
values in
the -
100% to plus infinity range. There are two tests to perform in sequence on
the nonconventional series to determine
if
there is
one
unique
or
multiple i':' val-
ues that are real numbers.
The
first test is the (Descartes') rule
of
signs which
249
250
CHAPTER
7
Rate
of
Return Analysis: Single Alternative
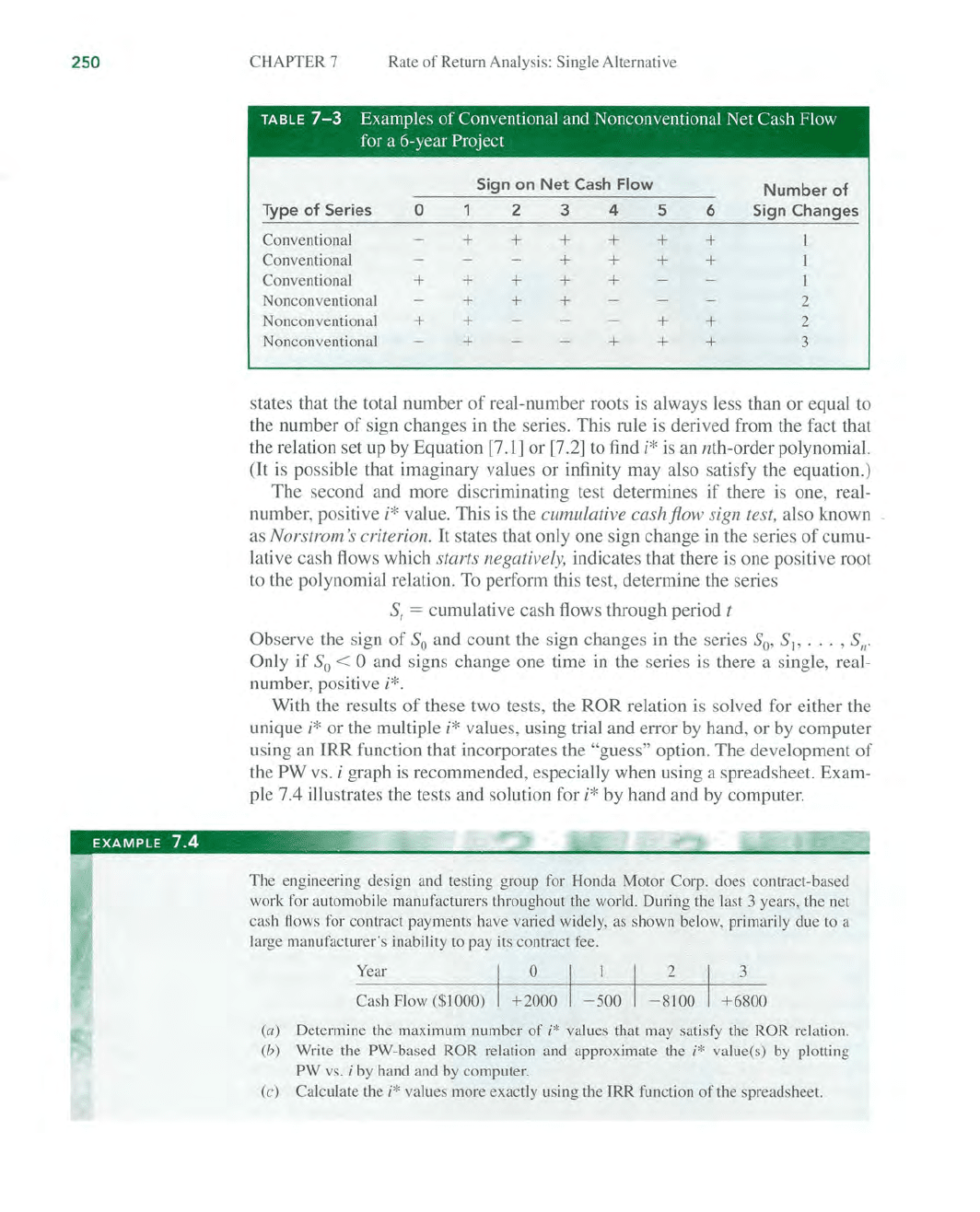
TABLE
7-3
Examples
of
Conventional and Nonconventional Net Cash Flow
for a 6-year
Project
Sign
on
Net
Cash Flow
Number
of
Type
of
Series
0 1 2 3 4
5 6 Sign
Changes
Conventional
+ + + +
+ +
Conventional
+ +
+ +
Conventional
+ + + + +
1
Nonconventional
+ + +
2
Nonconventional
+ +
+
+
2
Nonconventional
+ + +
+
3
states that the total number
of
real-number roots is always less than
or
equal to
the number
of
sign changes
in
the series. This rule is derived from the fact that
the relation set up by Equation [7.1]
or
[7.2] to find
i*
is an nth-order polynomial.
(It is possible that imaginary values
or
infinity may also satisfy the equation.)
The
second and more discriminating test determines if there is one, real-
number, positive
i*
value. This is the cumulative cash flow sign test, also known
as
Norstrom's criterion. It states that only one sign change in the series
of
cumu-
lative cash flows which
starts negatively, indicates that there is one positive root
to the polynomial relation. To perform this test, determine the series
51
= cumulative cash flows through period t
Observe the sign
of
So
and
count
the sign changes in the series
So'
51'
. . . ,
5".
Only if
So
< 0 and signs change
one
time
in
the series
is
there a single, real-
number, positive i*.
With the results
of
these two tests, the
ROR
relation is solved for either the
unique
i*
or
the multiple
i*
values, using trial and elTor by hand,
or
by computer
using an IRR function that incorporates the
"guess" option.
The
development
of
the
PW
vs. i graph is recommended, especially when using a spreadsheet. Exam-
ple 7.4
illustrates the tests and solution for
i*
by hand and by computer.
EXAMPLE
7.4
~
The
engineering design and testing group for
Honda
Motor
Corp
. does contract-based
work for automob
il
e manufacturers throughout the world.
During
the last 3 years, the net
cash flows for contract payments have varied widel
y,
as shown below, prim
ar
ily
due
to a
large manufacturer's inability to pay its contract fee.
Year
3
Cash Flow ($1000)
+
6800
(a) Determine the maximum number
of
i*
values that may satisfy the ROR rel
at
ion.
(b) Write the PW-based
ROR
relation and approximate the i* value(s) by plotting
PW
vs. i by hand and by computer.
(c) Calculate the
i*
values more
exac
tly using the
TRR
function
of
the spreadsheet.
SECTION 7.4 Mu
lti
ple Rate
of
Return
Va
lues
Solution by Hand
(a) Table
7-4
shows the annu
al
cash flows and cumulative cash flows. Since there are
two sign changes
in
the cash flow sequence, the rule
of
signs indicates a maximum
of
two real-number i* va
lu
es.
The
cumulati ve cash flow
se
quence starts with a pos-
itive number
So
=
+2
000, indicating there is not
ju
st
one
positive root.
The
conclu-
sion is that as many as two
i*
values can be found.
TABLE
7-4
Cash Flow and Cumulative Cash Flow Sequences, Example 7.4
Cash
Flow Sequence
Cumulative Cash Flow
Year
($1000)
Number
($1000)
0
+2
000
So
+2
000
I
-5
00
S,
+ 1500
2
- 8100
S2
- 6600
3
+68
00
S3
+2
00
(b) The
PW
relation is
PW = 2000 - 500(P / F,i, I) - 8100(P /
F,i
,2) + 6800(P / F,i,3)
Select values
of
i to find the two i* values, and plot PW vs.
i.
The
PW
values are
shown below and plotted
in
Figure 7- 5 for i values
of
0,5,
10
,2
0,30
, 40, and 50
%.
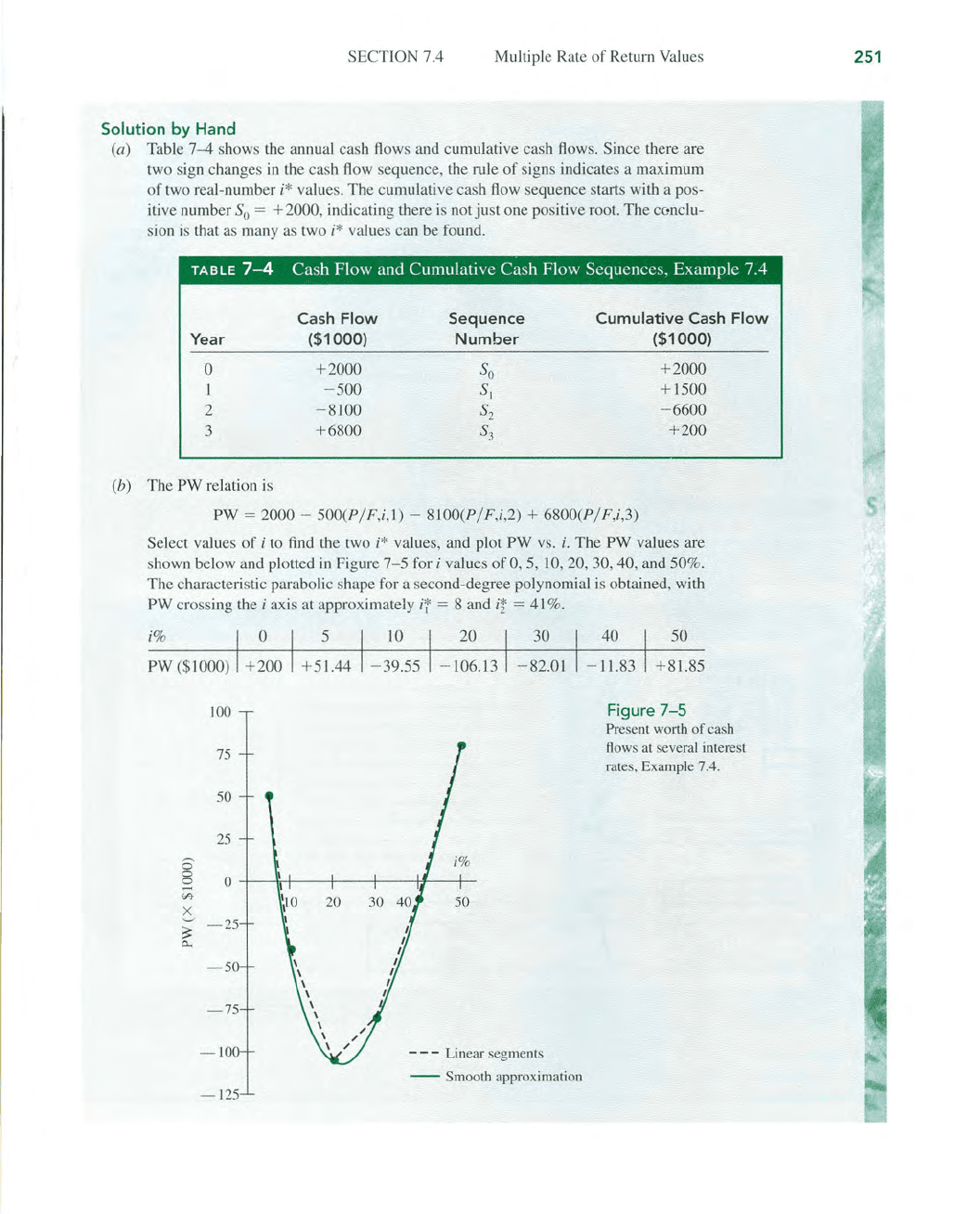
The characteristic parabo
li
c shape for a second-degree polynomial is obtained, with
PW crossing the i axis at approximately
if
= 8 and
ii
=
41
%.
i%
PW
($
1000
)
100
75
50
25
6'
0
0
S
""
x
~
-25
~
p"
-5
0
-7
5
-10
- 1
25
i%
50
- - - Linear segments
--
Smooth approximation
50
+8
1.
85
Figure
7-5
Present worth
of
cash
flows at several inte
re
st
rate
s,
Example 7
.4.
251
252
m
E·S
olve
CHAPTER 7 Rate
of
Return Analysi
s:
Single Alterna
ti
ve
Solution by Computer
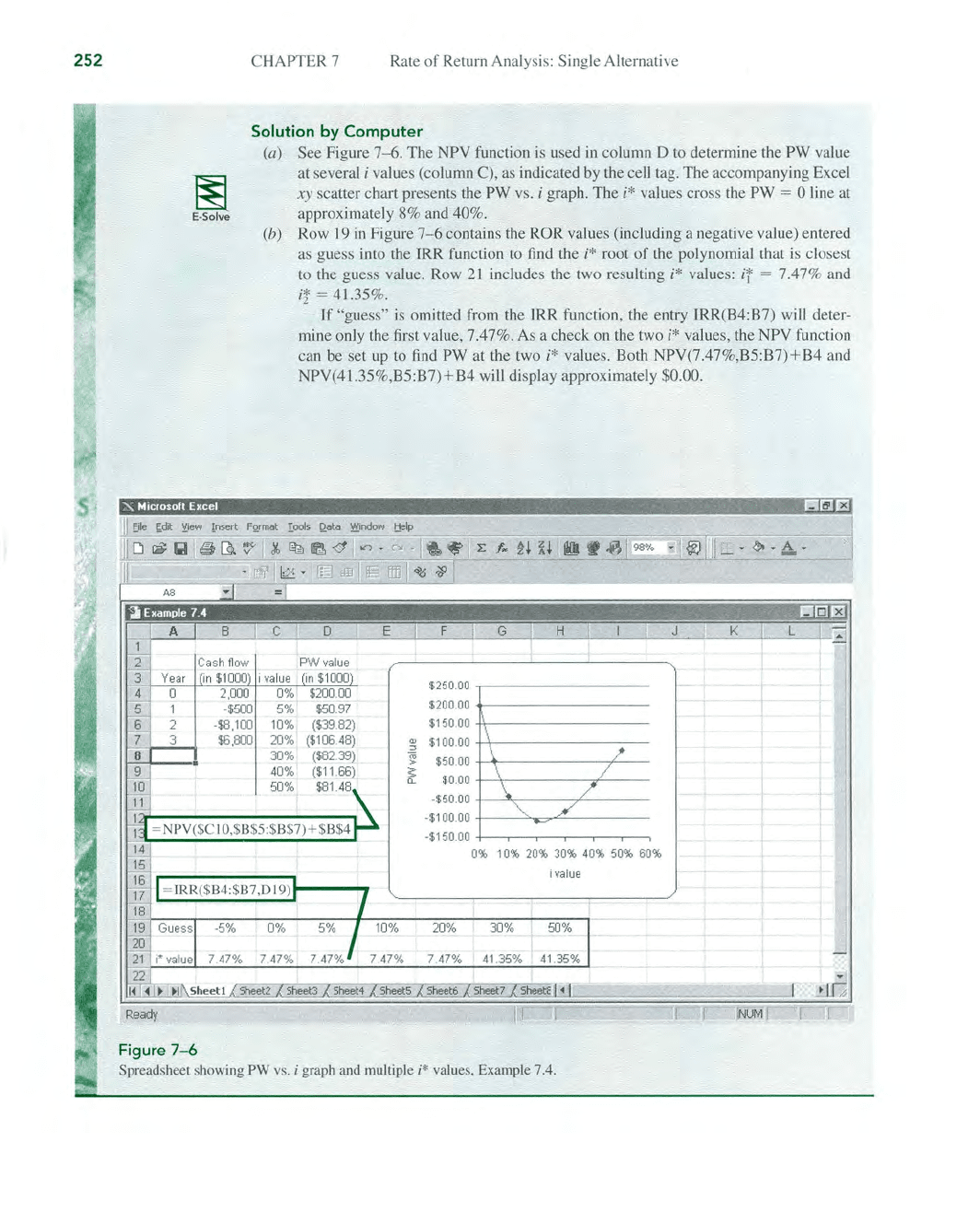
(a) See Figure 7- 6.
The
NPY function
is
used
in
column D to determine the PW value
at
several i values (column C), as indicated by the cell tag. The accompanying Excel
xy
scatter chart presents the PW vs. i graph.
The
i*
values cross the PW = 0 line at
approximately 8% and
40%.
(b) Row 19
in
Figure 7- 6 contains the ROR values (including a negative value) entered
as guess into the
TRR
function to find the i* root
of
the polynomial
th
at is closest
to the guess value. Row
2 I includes the two resulting
i*
values:
if
= 7.47% and
if = 41.35%.
If
"guess" is omitted from the
IRR
function, the entry IRR(B4:B7) will deter-
mine only the first value, 7.47%. As a check on the two
i*
values, the NPY function
can be set
LIp
to
find PW at the two
i*
values. Both NPY(7.47%,B5:B7)+
84
a
nd
NPY(41.35%,B5:B7)+ B4 will display approximately $0.00.
X Microsoft Excel
1!Ir;').Q
t
$250.
00
$200.00
$150.00
'"
$100.00
~
'"
$50.00 >
S
$0.
00
[L
-$50.
00
·$
10
000
\
\
/'
\ /
\
/'
"-
/'
-$150
.0
0
0%
10% 20% 30% 4
0%
50% 60%
i val
ue
20% 30%
Figure
7-6
Spreads
he
et showing PW vs. i graph a
nd
multiple i* values, Example 7.4.

SECTION 7.4
Multiple Rate
of
Return
Va
lu
es
EXAMPLE
7.5
::
Two student engineers started a software development business during their junior year
in
college. One package
in
three-dimensional modeling has now been licensed through
IBM's Small Business Partners Program for the next
10
years. Table
7-5
gives the
estimated net cash flows developed by
IBM
from the perspective
of
the small business.
The
negative values
in
years 1
,2,
and 4 reflect heavy marketing costs. Determine the number
of
i* va
lu
es; estimate them graphically and by the
IRR
function
of
a spreadsheet.
TABLE
7-5
Net Cash Flow Series and Cumulative Cash Flow Series,
Exam
pl
e 7.5
Cash Flow,
$100
Cash Flow,
$100
Year
Net
Cumulative
Year
Net
Cumulative
I - 2000 - 2000
6
+500
- 900
2 - 2000
- 4000
7 +400
- 500
3 +2500
-
1500
8
+ 300
- 200
4
- 500 - 2000
9
+200
0
5
+6
00
- 1400
10
+100 + 100
Solution by Computer
The
rule
of
signs indicates a nonconventional net cash flow series with
up
to three roots.
The cumulative net cash flow series starts negatively and has only one sign change
in
year
to, thus indicating that one unique positive root can be found. (Zero values
in
th
e cumula-
tive cash flow series are
ne
glected when applying Norstrom's criterion.) A PW-based ROR
relation
is
lIs
ed to find i*.
0 = -
2000(P/F
,i,l ) -
2000(P/F,i,2)
+
...
+
LOO
(P/ F,i,
LO
)
The
PW
of
th
e
ri
ght s
id
e
is
calculated for different values
of
i and plotted on
th
e spread-
sheet (Figure 7-7).
The
unique value i* = 0.
77
%
is
obtained using the
IRR
function with
the same
"g
uess" values for i as
in
the
PW
vs. i graph.
Comment
Once the spreadsheet is set
up
as in Figure 7-7, the cash flows can be "tweaked" to perform
sensiti
vi
ty
ana
ly
s
is
on
th
e i* value(s). For example,
if
the cash flow in year
10
is
changed
only slightly from
$+
100
to
$-
100,
the
re
sults displayed change across the spreadsheet to
i*
= - 0.84%. Also, this simple change
in
cash flow substantially alters the cumulative
cash flow sequence. Now
SIO
=
$-
100,
as can be confirmed
in
Table 7-
5.
There are now
no sign changes
in
the cumulative cash
flo
w sequence, so no unique positi
ve
rool can be
found. This is confirmed by
th
e value i* = - 0.84%.
If
other cash flows are altered, the two
tests we have l
ea
rned should be appljed
to
determine whether multiple roots may now
exist. This means
th
at spreadsheet-based sensitivity analysis must be performed carefully
when the
ROR method is applied, because not all i* values may be determined as cash
flows are tweaked on the scree
n.
253
m
E-Solve

254
CHAPTER
7 Rate
of
Return Analysis:
Single
Alternative
X Microsoft Excel
,~
!
clF&18;!~M'
KJ
"'"':
.ma
1
2
3
Year
4 0
5 1
6 2
2J
3
J\ji
jl
Cas
h
flow
$
$
(2,000)
$
(2,000)
$ 2,500
$
(500)
$ 600
$ 500
$
400
$
300
$ 200
$ 100
i
va
lue
·10%
-5%
0%
1%
5%
10%
PIN
value
$2,269
$946
$100
($29)
($450)
($811)
$200
,----------
$O~~-------
-$200
+-~----",
~
",,-
----
-$400
-t---
- -
""''''~~----
-$600
-t------~'-~--
-$800
-t--------~
-$1,000
-l--r---r--,-
-
.----,
0%
2%
4%
6% 8%
10%
..
...
J
.~.A.
~
- -
--
-
---
_ !:l X
L
~
15
r--------------------,
i
value
16
=N
PV($C7,$B$5:$B$14)+$B$4
17
18
-10% -5%
0%
0.77% 0.77% 0.77%
1%
5%
10%
0.77% 0.77%
Sheet!
Sheet2,
Sheet3.
,Gheet4
SheetS
Sheet6 Sheetl
Ready
Figure
7-7
Spreadsheet solution to
find
i*, Example 7.
5.
In many cases some
of
the multiple
i*
values will seem ridiculous because
they are too large or too small (negative). For example, values
of
10, 150, and
750% for a sequence with three sign changes are difficult to use in practical
decision making. (Obviously, one advantage
of
the
PW
and AW methods for
alternative analysis is that unrealistic rates do not enter into the analysis.) In de-
termining which
i*
value to select as the
ROR
value, it is common to neglect
negative and large values
or
to simply never compute them. Actually, the correct
approach is
to
determine the unique composite rate
of
return, as described
in
the
next section.
If
a standard spreadsheet system, such as Excel,
is
used, it will normally deter-
mine only one real-number root, unless different
"g
uess" amounts are entered
sequentially. This one
i* value determined from Excel is usually a realistically val-
ued root, because the
i*
which solves the
PW
relation
is
determined by the spread-
sheet's built-in trial-and-error method. This method starts with a default value,
commonly 10%, or with the user-supplied guess, as illustrated in the previous
example.
