Blank L., Tarquin A. Engineering Economy (McGraw-Hill Series in Industrial Engineering and Management)
Подождите немного. Документ загружается.


SECTION 8.4 Rate
of
Return Evaluation Using PW: Incremental and Breakeven
TABLE
8-4
Incremental Cash Flow Tabulation, Example 8.3
Incremental
Year Cash Flow A Cash Flow B Cash Flow
(1
) (2)
(3) = (2) - (1)
0 $
- 8,000
$-
13
,000
$ - 5,000
1- 5
- 3,500 - 1,600 +1
,9
00
5
{
+
2,
000
- 13,000
-11,000
6-
10
- 3,500 - 1
,6
00 + 1,900
10
+2,000
+2,
000
$- 43,000
$-38,
000
$
+5
,000
Determine which vendor should be selected if the MARR
is
15
%
per
year. Show hand and
computer so
Juti
on
s.
Solution
by
Hand
These are service alterna
ti
ves, s
in
ce all
ca
sh flows are costs. Use the procedure described
above to determine
Ci
i~
_ A
'
J.
Alternatives A and B are correctly ordered with the
hi
gher
fir
st-cost alternative
in
coJ-
umn (2).
2.
The
cash flows for the
LCM
of
10 years are tabulated
in
TabJe
8-4.
3.
The
incremental cash flow diagram is shown in Figure
8-l.
4. There are three sign changes in the incremental cash flow series, indicating as many as
three roots. There are also three sign changes
in
the cumulative incremental series,
which starts negatively at
So = $- 5000 and continues to
SIO
= $+5000, indicating
that more than one positive root may exist.
5.
The
rate
of
return equa
ti
on based on the
PW
of
in
cremental cash flows is
0=
- 5000 + I 900(P/ A,
Cii
,
10
) -
1l
,000(P/ F,Cii,5) + 2000(P/ F,Cii,10) [8.2]
$
1900
o 2 3
4
5 6
$
5000
$
IJ
,
OOO
7
8
9
$20
00
t
10
Figure 8-1
Diagram of
in
creme
nt
al
cas
h
flow
s,
Examp
le 8.3.
285

286
CHAPT
ER
8 Rate
of
Return Analysis: Multiple Alternatives
Assume that the reinvestment rate
is
equal to the resulting
~it
- A
(or
~i*
for a short-
ened symbol
).
Solution
of
Equation [8.2] for the first root discovered results
in
~i
':'
between
12
and
15
%.
By
interpolation
~i
*
= 12.65%.
6.
Since the rate
of
return
of
12.65% on the extra investment is less than the
15
%
MARR
, the lower-cost vendor A is selected.
The
extra investment
of
$5000 is not eco-
nomically
ju
stified by the lower annual cost and higher salvage estimates.
Comment
In step 4, the presence
of
up to three
i*
values
is
indicated.
The
preceding analysis finds one
of
the roots at 12.65%. When we state that the incremental
ROR
is 12.65%, we assume that
any positive net-investments are reinvested at c
= 12.65
%.
If
this
is
not a reasonable as-
sumption, the net-investment procedure must be applied and an estimated reinvestment
rate c
mu
st be used to find a different value
~i'
to compare with MARR =
15
%.
X M,cros
oft
EHcel - EHample 0.3 ,
I!I~
t3
DIS
A
MARR
=
Yea
l-
o
2
3
4
5
6
7
8
9
10
In
cremental
j'
Fi
gur
e
8~2
Vendor A
$
(8,000)
$ (3,500)
$ (3,500)
$ (3,500)
$ (3,500)
$ (3,500)
$ (3,500)
$ (3,500)
$ (3,500)
$ (3,500)
$ (3,500)
Incremental
Vendor B cash flow
$
(13,000) $ (5,000)
$ (1,600) $ 1,900
$ (1,600) $ 1,900
$ (1,600) $ 1,900
$ (1,600) $ 1,900
$
(1
2,600) $ (9, 1
00
)
~
=
Clo~Blo
l
$ (1,600) $
1,90
~
I
$ (1,600) $ 1,900
$ (1,600) $ 1,900
$ (1,600) $ 1,900
$ 400
,...;:;..$
_.,.;;
3
:.:,.;'
9
;;.,;;;0,;;,0.,
~
12
.65%
-;;
~
= NPV($0$
15
,D5:014
)+D4
1
$000
""""""'"
I
($438
91
:-)...
--.J
=
N
~
PV
;;:
(
;;
$
~
B
$
;;
I
-;:
,
0
::-:;
5
-;:
:0
::
1
-;
4
)
:-:
+
-::
0
::::1
41
Spreadsheet
So
lulion to
find
th
e
in
cremental rate
of
return, Example 8.3.
..!.J
r
r

SECTION 8.4 Rate
of
Return Evaluation Using PW: Incremental and Breakeven
The other two roots are very large positive and negative numbers, as the IRR function
of
Excel reveal
s.
So
they are not u
sef
ul
to the analysis.
Solution
by
Computer
Steps I through 4 are the same as above.
5. Figure
8- 2 includes the incremental net cash flows from Table
8-4
calculated
in
column D.
Ce
ll
D15
di
splays the
t.i
* value
of
12
.65% using the IRR function.
6. Since the rate
of
return on the extra investment is less than the
15
%
MARR
, the
lower-cost vendor A is selected.
Comment
Once the spreadsheet is set up, there are a wide variety
of
analyses that can be performed.
For example, cell D
17
uses the NPY function to verify that the present worth is zero at the
calculated
t.r
:'
. Cell D
18
is
the
PW
at
MARR
= 15%, which is negati ve, thus indicating
in
yet another way that the extra investment does not return the MARR.
Of
course, any
cash
flow
estimate and the
MARR
can be changed to determine what happens to t.i*. A
PW vs.
t.i
chart could easily be added, if two more columns are inserted, similar to those
in
Figures 7
-6
and 7-
7.
The rate
of
return determined for the incremental cash flow series can be in-
terpreted as a
breakeven rate
of
return value.
If
the incremental cash flow
ROR
(Lli
':'
)
is
greater than the
MARR,
the larger-investment alternative is selected.
For example, if the
PW
vs. i graph for the incremental cash flows in Table
8-4
(a
nd
spreadsheet Figure
8-2)
is plotted for various interest rates, the graph
shown
in
Figure
8-3
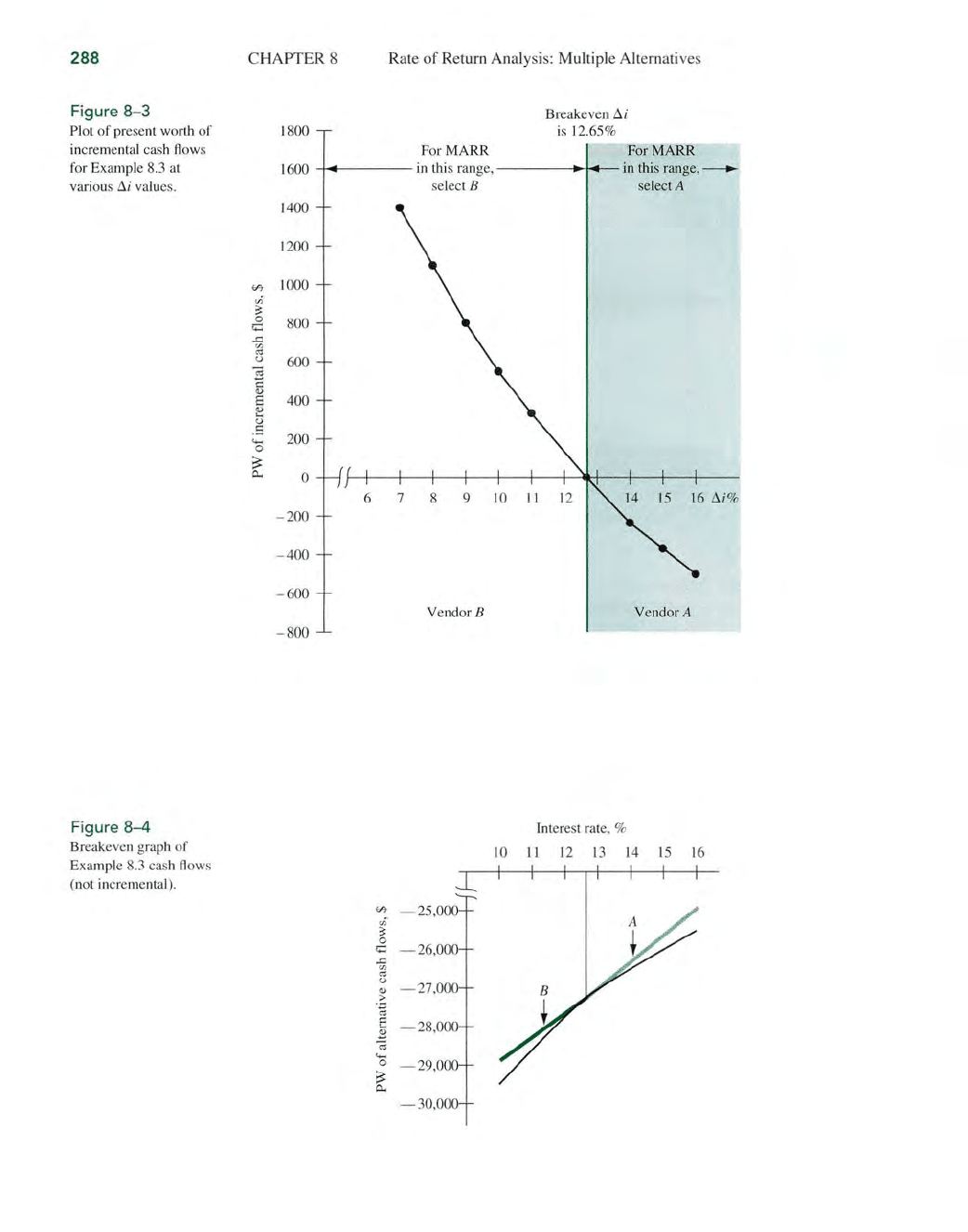
is obtained. It shows the Lli* breakeven at 12.65%. The
conclusions are that
• For
MARR
< 12.65%, the extra
in
vestment for B is
ju
stified.
• For
MARR
> 12.65%, the opposite is true; the extra investment
in
B should
not be made, and vendor A
is
selected.
• If
MARR
is
exactly 12.65%, the alternatives are equally attractive.
Figure
8-4,
which is a breakeven graph
of
PW
vs. i for the cash flows (not incre-
mental)
of
each alte
rn
ative
in
Example 8.3, provides the same results. Since all
net cash flows are negative (service alternatives), the
PW
values are negative.
Now, the same conclusions are reached using the following logic:
• If
MARR
<
12
.65%, select B since its
PW
of
cost cash flows is smaller
(numerically larger).
•
If
MARR
>
12
.
65
%, select A since now its
PW
of
costs is smaller.
• If
MARR
is exactly 12.65%, either alternative is equally attractive.
The next example illustrates incr
eme
ntal
ROR
evaluation and breakeven rate
of
return graphs for reve
nu
e alternatives.
More
of
breakeven analysis is covered in
Chapter
13.
287
~
E·
Solve
( Cha
p
-]
13
288
Figure 8
-3
Plot of prese
nt
worth of
in
creme
nt
al cash Hows
for Example 8.3 at
va
ri
ous tli
va
lu
es.
Figure
8-4
Br
ea
keven graph of
Exam
pl
e 8.3 cash Hows
(not
in
creme
ntal
).
CHAPTER 8
1800
Rate
of
Return Analysis:
Mu
ltiple Alternatives
Breakeven
tli
is 12.
65
%
Fo
r MARR For MARR
1600
-+01--
-
---
in
thi
s range,
--
--_~+
..
I--
in
this range,_
1400
1200
""
1000
ul
~
0
800
..::
.c
'"
'"
u
S
600
~
E 400
1:
u
.:
200
4-<
0
~
P..
0
6
-2
00
- 400
- 600
- 800
select B select A
""
t
o
I+:
~
'"
u
'"
>
:;;
Vendor B
"
~
-28,
000
0;
4-
; - 29,000
P..
-3
0,00
Vendor A
I
nt
erest
ra
te, %
10
11
12
13
14 15 16

SECTION 8
.4
Rate
of
Return Eva
lu
ation Us
in
g PW: Incremental and Breakeven
EXAMPLE
8.4 '
~
Ba
nk
of America uses a MARR
of
30% on alternatives for i
ts
own business that are con-
s
id
ered
ri
sk
y,
th
at is, the respo
ns
e
of
the public to the service has not been well estab-
li
shed
by
t
es
t marketing. Two alternative software systems and the marketing/delivery
pl
ans have been jointly developed by software engineers and the marketing department.
Th
ey are for new online banking and loan services to passenger cruise ships and military
vessels at sea inte
rn
ationally. For each system, start-up, annual net income, and salvage
va
lu
e (i.e., se
ll
-out value
to
another
fi
nancial corporation) estimates are summarized
bel
ow.
(a) Perfo
rm
th
e incremental ROR analysis
by
computer.
(b) Develop
th
e PW vs. i graphs for each alternative and the increment. Which altern
a-
ti v
e,
if either on
e,
should be selected.?
Initial i
nv
estment, $1000
Estimated net income,
$
1000 per year
Sa
lv
age value, $1000
Estimated com
pe
titive
lif
e,
years
Solution by
Computer
Sys
t
em
A
- 12,000
5,000
2,500
8
System
B
-
18
,000
7,000
3,000
8
(a)
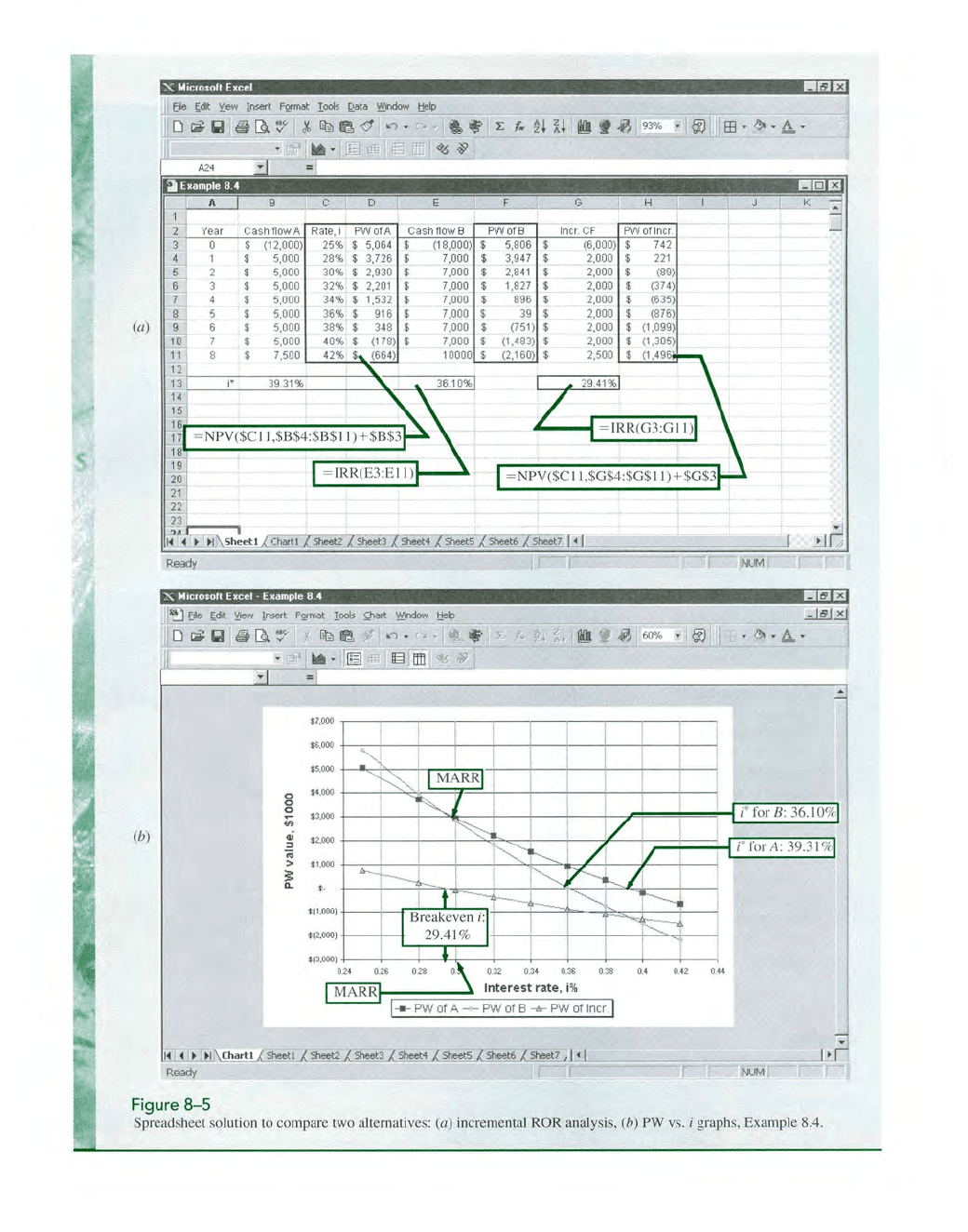
Refer to Figure 8- 5a. The IRR function
is
used in cells B
13
and E13 to display
i*
for each alte
rn
ative.
We
use the
i*
values
as
a preliminary screening tool only to
determine
whi
ch alte
rn
a
ti
ves exceed
th
e MARR.
If
none do, the DN alternative
is
ind
icated automatically. In bo
th
cases
i*
> 30
%;
they are both retained. The incre-
mental cash
fl
ows are calculated (column G = column E - column B), and the IRR
fu
nction r
es
ults
in
Ili* = 29
.41
%. This value is slightly less than the MARR; alter-
na
ti
ve A is selected as
th
e better economic choice.
(b) Figure 8-
5b
conta
in
s
pl
ots
of
PW vs. i for all three cash
flow
series between the
inter
es
t rates
of
25 and 42
%.
The bottom curve (incremental analysis) indicates
th
e breakeven ROR at 29
.41
%,
which is where the two alternative
PW
curves cross.
The conc
lu
sion is aga
in
th
e same; with MARR = 30
%,
select alternative A because
i
ts
PW va
lu
e ($2930
in
ce
ll
D5
of
Figure 8- 5a) is slightly larger than that for B ($2841
in
F5
).
Comment
With th
is
spreadsheet
fo
rmat, both a PW analysis and
an
incremental ROR analysis have
be
en
accomp
li
shed with gra
phi
c backup to demonstrate the conclusion
of
the engineering
economy ana
ly
sis.
289
~
E-Solve
(a)
(b)
X Microsoft Excel I!!lral3
'iI Example 8 4 I!!lIiII3
A B C D E
H
Y
ea
r Cash
fiowA
Rate
, j
PWofA
Cash
fi
ow B
PWofB
Inc
r.
CF
PW oflner.
3 0 $
(12,00
0)
25%
$
5,064
$
(
18,000
)
$
5,806 (6,000)
$ 742
4
$
5,000
28%
$
3,726
$
7,000
$
3,947 2,000
$
221
5
5,000 30% $ 2,930 $
7,000
$
2,841 2,000 $
(89)
6
5,000 32%
$
2,201
$
7,000
$
1,827
2,000
$
(374)
7
5,000
34%
$
1,532 $ 7,000
$
896
2,000 $ (635)
8
5,000
36%
$ 916 $
7,000
$
39 2,000
$
(876)
9
5,000
38%
$ $ 7,000 $
(751)
2,000 $
(1
,099)
10
5,000 40%
$
7,000
$ (1,483)
2,000
$ (1,305)
11
7,
500
42%
10000
$
(2,160) 2,500 $ (1, 496
12
13
j'
39.
31%
29.41%
14
15
16
17
= IRR(G3:G I I)
18
19
20
= NPV($C II ,$G$4:$G$ II
)+$G$3
21
22
23
I
~
~ ~
Ready
X M,c,o.on Excel · Example 8 4
l!!lra
13
$7.000
$6,000
$5.000
0
$4.000
0
0
$3,000
;;
oj
S2.000
:l
ii
>
$1,000
:s:
"-
$.
$(1,000)
$
12
.000)
I
I I I
~
I
I
I
~
~
A
~
,
!
1'..
I I
I
I
~
I
/ ,
I
I
,~
~
I
/1
V
,
I
,
f----
I
i'--,y----,
'--.
/1
I
,
t
-
~
~
--l~
'------.
I
I
1 Breakeven
i:
11
I
""""""-
,
!
I
,;:::-
I
29
.41
%
I
,
,
1
,
;
$(3,000)
0.24
0
.2S
0
.28
0.\ 0.
32
0.
34
0.3&
0.
38
0,4
0.42 O.H
~
Interest
rate
, i%
, .....
PW
of
A
~
PW
of
B
-.>-
PW
of
Incr
.'
~
.e
t.!..bb
eet
lli
he.!:.t3
,-"-,=="-"=",-,,-,,,,=,-,,-=,,,,,---,L
tl
Ready
i* for
B:
36. I 0%1
i' for
A:
39.3 l %1
NUM
Figure
8-5
Spreadsheet solution to
co
mpare two alterna
ti
ves: (a) incremental ROR analysis, (b) PW vs. i graphs, Example 8.4.

SECTION 8.5 Rate
of
Return Evaluation Using
AW
Figure
8-Sb
provides an excellent opportunity to see why the
ROR
method
can result in selecting the wrong alternative when only
i*
values are used to se-
lect between two alternatives. This is
sometimes
ca
ll
ed
the ranking
inconsistency problem
of
the
ROR
method. The inconsistency occurs when the
MARR is set less than the breakeven rate between two revenue alternatives.
Since the
MARR
is established based on conditions
of
the
economy
and
mar
-
ket,
MARR
is
established external to any particular alternative evaluation. In
Figure
8-Sb, the breakeven rate is 29.41 %, and the
MARR
is 30%.
If
the
MARR
were established
lower
than breakeven, say at 26%, the incremental
ROR
analysis results
in
correctly selecting B,
because
!1i*
= 29.41 %, which
exceeds 26%.
But
if only the
i*
values were used, system A
would
be
wrongly
chosen, because its
i*
= 39.31
%.
This
error
occurs
because
the rate
of
return
method assumes
reinvestment
at the alternative's
ROR
value (39.31 %), while
PW
and AW analyses use the
MARR
as the reinvestment rate.
The
conclusion
is
simple:
If
the
ROR
method
is
used to evaluate two
or
more alternatives, use the
incremental cash flows
and
.:li* to make the decision between alternatives.
8.5
RATE
OF RETURN EVALUATION USING
AW
Comparing alternatives by the
ROR
method (correctly performed) always leads
to the same selection as
PW,
AW,
and
FW
analyses, whether the
ROR
is deter-
mined using a
PW-based, an AW-based,
or
a
FW
-based relation. However, for the
AW-based technique, there are two equivalent ways to perform the evaluation:
using the
incremental cashflows over the
LCM
of
alternative lives,
just
as for the
PW-based relation (previous section),
or
finding the A W for each alternative's
actual cash flows and setting the difference
of
the two equal to zero to find the
!1i*
value.
Of
course, there is no difference between the two approaches
if
the
alternative lives are equal. Both methods are summarized here.
Since the
ROR
method requires comparison for equal service, the incremen-
tal cash flows must be evaluated over the
LCM
of
lives. When solving by hand
for
!1i*,
there may be no real computational advantage to using A
W,
as was found
in Chapter 6. The same six-step procedure
of
the previous section (for
PW
-based
calculation) is used, except in step 5 the AW-based relation is developed.
For comparison by computer with equal
or
unequal lives, the incremental cash
flows must be calculated over the
LCM
of
the two alternatives' lives. Then the
IRR function is applied to find
!1i*.
This is the same technique developed
in
the
previous section and used in the spreadsheet in Figure
8-2. Use
of
the IRRfunc-
tion
in
this manner is the correct way to use Excel spreadsheet functions to com-
pare alternatives using the ROR method.
The second A W-based method takes advantage
of
the AW tech
nique's
assump-
tion that the equivalent
AW
value is the same for each year
of
the first and all suc-
ceeding life cycles. Whether the lives are equal
or
unequal, set up the A W relation
for
the cash flows
of
each alternative, form the relation below, and solve for
i*.
0=
AW
B
-
AW
A
[8.3]
Equation [8.3] applies to solution by hand only, not solution by computer.
291
~
E·Solve
AW and
li
fe
cycles

292
CHAPTER S Rate
of
Return Analysis: Multiple Alternatives
For both methods, all equivalent values are on an AW basis, so the i* that results
from Equation [8.3] is the same as the
t:.i*
found using the first approach. Exa
m-
ple 8.S illustrates
ROR
analysis using AW-based relations for unequal lives.
EXAMPLE
8.5
~_c'
Compa
re the alte
rn
a
ti
ves
of
vendors A and B for Verizon Communi
cat
ions
in
Exam-
ple
S.3, us
in
g an
AW-
ba
se
d incremental
ROR
method and the
sa
me
MARR
of
15
%
per year.
Solution
For
reference, the PW-based
ROR
relation, Equation
[S
.2], for the
in
cremental cash
fl
ow in Example S.3 shows that vendor A should be selected with I:li* = 12.65%.
For
the
AW
relation, there are two equivalent solution approache
s.
Write an
AW-
based relation on the incremental cash flow series over the
LCM
of
10
years, or write
Equation
[S.
3) for the two actual cash flow se
ri
es over one life cycle
of
each alte
rn
ative.
For the incremental method, the AW equation is
0 = - 5000(A/P,l:li,1O) - 1l,000(P/F,l:li,S)(A/P,l:li,IO) +
2000(A
/F,l:li,]0) +
1900
It
is easy to enter the incremental cash flows onto a spreadsheet, as
in
Figure S-2,
column D, and use the
IRR
(D4:D14) function to display
I:li*
= 12.65%.
For
the second method, tbe
ROR
is found by Equation [S.3) using the respec
ti
ve
lives of
10
years for A and 5 years for B.
AW
A
=
-S
OOO
(A/
P,i,lO) - 3500
AWs =
-13,000(A
/ P,i,5) + 2000(A/ F,i,5) - 1600
Now develop 0 = AW
B
-
AWN
0 = - 1
3,
000
(A/
P,i,5) + 2000(A/ F,i,5) +
SOOO(A
/P,i,
10
) + 1900
Solution
aga
in
yields an interpolated value
of
i* = 12.65%.
Comment
It
is very important to remember that when
an
incremental
ROR
analysis us
in
g an
AW-
based equation
is
made on tbe incremental cash flows, the least common mUltiple
of
lives must be used.
8.6
INCREMENTAL ROR ANALYSIS
OF
MULTIPLE,
MUTUA
LLY
EXCLUSIVE ALTERNATIVES
This section treats selection from multiple alternatives that are mutua
ll
y exclu-
sive, us
in
g
th
e
in
cremental
ROR
method. Acceptance
of
one
alternative automat-
ica
ll
y precludes acceptance
of
any others.
The
analysis is based upon PW (or AW)
relations for
in
cremental cash flows between two alternatives at a time.
When the
in
cremental
ROR
method is applied, the entire
in
vestment
mu
st
return at least the
MARR.
When the i* values on several alternatives exceed the
MARR,
in
cremental
ROR
evaluation is required. (
For
revenue alternatives, if

SECTION 8.6
Incremental
ROR
Analysis
of
Multiple, Mutually
Exclusive
Alternatives
not even
one
i*
:2:
MARR, the do-nothing alternative is selected.)
For
all alter-
natives (revenue
or
service), the incremental investment
must
be separately
justified.
If
the return on the extra investment equals
or
exceeds the
MARR,
then
the extra investment should be
made
in order to maximize the total return on the
money available, as discussed in Section 8.1.
Thus, for ROR analysis
of
multiple, mutually exclusive alternatives, the follow-
ing criteria are used. Select the
one
alternative that
1.
Requires the largest investment, and
2. Indicates that the extra investment over another acceptable alternative
is
justified.
An important rule to apply when evaluating multiple alternatives by the incre-
mental ROR method
is
that an alternative should never be compared with one
for
which the incremental investment is not justified.
The
incremental ROR evaluation procedure for multiple, equal-life alterna-
tives
is
summarized below. Step 2 applies only to revenue alternatives, because the
first alternative is compared to
DN
only when revenue cash flows are estimated.
The
terms defender and challenger are dynamic in that they refer, respectively, to
the alternative that
is
currently selected (the defender) and the
one
that is chal-
lenging it for acceptance based on l1i*. In every pairwise evaluation, there is
one
of
each.
The
steps for solution by hand
or
by
computer
are as follows:
I. Order the alternatives from smallest to largest initial investment. Record the
annual cash flow estimates for each equal-life alternative.
2.
Revenue alternatives only: Calculate
i*
for the first alternative. In effect, this
makes DN the defender and the first alternative the challenger.
If
i*
<
MARR,
eliminate the alternative and go to the next one. Repeat this
until
i*
:2:
MARR
for the first time, and define that alternative as the defender.
The
next alternative
is
now the challenger.
Go
to step
3.
(Note: This is where
solution
by
computer spreadsheet can be a quick assist. Calculate the
i*
for
all alternatives first, using the
IRR
function, and select as the defender the
first one for which
i*
:2:
MARR. Label it the defender and
go
to step 3.)
3.
Determine the incremental cash flow between the challenger and defender,
using the relation
Incremental cash flow
= challenger cash flow - defender cash flow
Set up the
ROR
relation.
4. Calculate
l1i*
for the incremental cash flow series using a
PW
-, AW-,
or
FW-based equation.
(PW
is most commonly used.)
5.
If
l1i*
:2:
MARR,
the challenger becomes the defender and the previous
defender
is
eliminated. Conversely,
if
l1i*
<
MARR,
the challenger is
removed, and the defender remains against the next cha
ll
enger.
6. Repeat steps 3 to 5 until only
one
alternative remains.
It
is the selected one.
Note that only two alternatives are compared at
anyone
time.
It
is vital that the
correct alternatives be compared,
or
the wrong alternative may be selected.
293
Q-Solv
294
CHAPTER 8
Rate
of
Return Analysis: Multiple Alternatives
EXAMPLE
8.6
"
Caterpillar Corporation wants
to
build a spare parts storage facility
in
the Phoenix,
Arizona, vicinity. A plant engineer h
as
identified four different location options. Initial
cost of earthwork and prefab building, and annual net cash flow estimates are detailed
in
Table
8-5
. The annual net cash
flow
series vary due
to
differences
in
ma
int
enance,
labor costs, transportation charges, etc. If the MARR
is
10
%,
use
in
cremental ROR
a
nal
ysis
to
select the one economically best location.
TABLE
8-5
Estimates for Four Alternative Building Locations,
Example 8.6
Initial cost, $
Annual cash
flow
, $
Life, years
Solution
A
-2
00,000
+ 22,000
30
B
- 275,000
+3
5,000
30
c
-190
,000
+ 19,500
30
D
- 350,000
+42,
000
30
All sites have a 30-year life, and they are revenue alternatives. The procedure outlined
above is applied.
I. The alternatives are ordered
by
increasi
ng
initial cost
in
Table 8-6.
2.
Compare location C with the do-nothing alternative. The ROR relation includes
o
nl
y
th
e PIA factor.
0=
-
190
,000 + 19.500(PIA,i*,30)
Table
8-6,
column 1, presents the calculated (P I
A
,
~i
*,3
0
)
factor value
of
9.7436
and
~i
~
= 9.63%. Since 9.63% < 10%, location C is eliminated. Now
th
e com-
parison is A to DN, and column 2 shows that
~i
!
= 10.49%. This eliminates the
do-nothing alternative; the defender is now A and the challenger is
B.
TABLE
8-6
Computation
of
Incremental Rate
of
Return for Four
Alternatives, Example 8.6
C
A
B
(1
)
(2)
(3)
D
(4)
Initial cost, $ - 190,000 - 200,000 - 275,000 - 350,000
Cash flow, $ +
19
,500 +22,000 +35,000 + 42,000
Alternatives compared
CtoDN
AtoDN
B
toA
DtoB
Incremental cost, $ - 190,000
-2
00,000
-
75
,000
-
75
,000
Incremental cash
flow,
$
+ 19,500
+22,
000 + 13,000 + 7,000
Calculated
(
P
IA,
~i
*,3 0)
9.7436 9.0909 5.7692
10
.7
14
3
~i
*
,%
9.
63
10.49
17
.28 8.55
Increment justified?
No
Yes
Yes
No
Alternative selected DN A
B
B
