Білинський, Й.Й. Методи обробки зображень в комп’ютеризованих оптико-електронних системах: монографія

Подождите немного. Документ загружается.

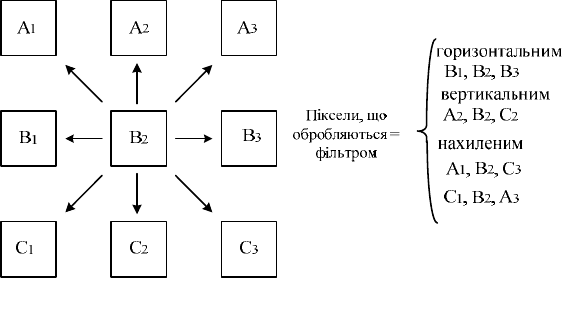
пристрій, аналізуючи параметри цієї примежової кривої, формує га-

уссовий фільтр у вигляді однонаправленої маски

*( )Gn

з певними

. За такої

те-

ваговими коефіцієнтами та розмірністю вікна допомогою

маски виконується повторна фільтрація в околі максимуму градієнта

примежової кривої. Результатом повторної фільтрації є розподіл ін

нсивності примежової кривої

**( )Sn

, а результатом знаходження спі-

льної точки перетину примежових кривих

*( )Sn

**( )Sn

є координа-

ти краю

()n

()m

об’єкта на зображе [171].

На відомі й шес-

подання .

нні,

трикутна

відповідно

зображення

Слід зауважити, що однонаправлена маска гауссового фільтра може

мати різний набір положень (залежно від кількості можливих напря-

мків), які визначаються структурою періодичної просторової ґратки

матричного приймача.

етрії

сьогодні

цифрового

квадратна

[161]тикутна форма геом

Так, наприклад, для матричного приймача з пікселами, що

мають квадратну форму, кількість можливих варіантів однонаправле-

ної маски гауссового фільтра відповідає чотирьом (рис. 3.5).

для м

Рис. 3.5. Варіанти однонаправлених масок

атричного приймача з квадратною формою пікселів

В результаті обходу виділеного контуру аналізується поло-

ження контурного піксела відносно попереднього та визначається йо-

100

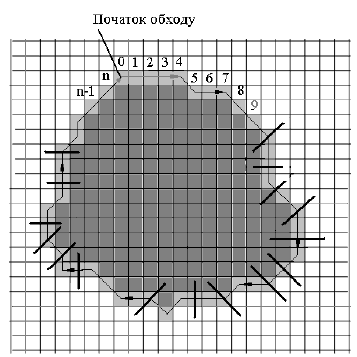
го орієнтація. Приклад обходу контуру зображення об’єкта та визна-

чення його орієнтації наведений на рис. 3.6.

Для визначення субпікселних координат контуру необхідно

знайти субпікселні зміщення

відносно центра контурних пік-

селів. При цьому необхідно застосувати дві однонаправлені маски за-

даної орієнтації. Залежно від ння кута нахилу контуру можуть

бути застосовані дві пари однонаправлених к г их фільтрів.

Якщо кут уру близький до 45

або 135

, то викорис

значе

масо ауссов

нахилу конт тову-

ються горизонтальна та вертикальна маски. Якщо ж кут нахилу кон-

туру близький до 0

або 90

, то використовують вертикальну та нахи-

лену або горизонтальну та нахилену маску, відповідно.

Рис. 3.6. Приклад обходу контуру зображення об’єкта

при використанні однонаправленої маски фільтра

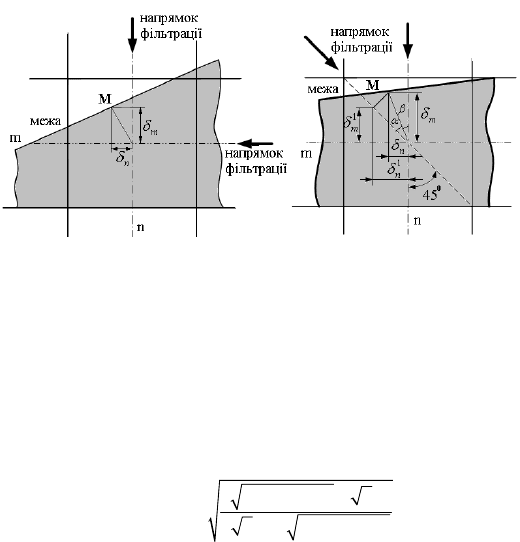
На ри що попада-

ють на 45

при куті нахилу близькому до 0 , а також напрямки їх фільтрації та

субпікс

с. 3.7а і б наведені межі зображення об’єкта,

піксел з координатами n, m при куті нахилу близькому до

елні координати в точці М, відповідно. При цьому вважається,

що інтенсивність по всій площі піксела є рівномірною.

101

Субпікселне зміщення

відносно центра піксела при куті нахи-

лу межі близькій до 0

визначається за допомогою субпікселних коор-

динат, отриманих за допомогою нахиленої маски як

12 1 2

3( ) ( ) 2

22 ( ) ( )

nm m

mn m

δδ

δδδ

+−

=±

−+

, (3.4)

де

– субпікселні зміщення межі відносно центра піксела при

використанні нахиленої маски.

Рис. 3.7. Знаходження субпікселних координат межі зображення

об’єкта при різних кутах нахилу контуру

У випадку нахилу межі близькій до 90

0о

субпікселна коорди-

ната

визначається згідно з (3.4).

на основі його дискретного подання

ри призводить

до великого згладження кута повороту, що не завжди відповідає дійс-

3.2. Відновлення неперервного контуру

Форма об’єкта описується його неперервним контуром який

можна отримати внаслідок апроксимації. Кількість відрізків, якими

апроксимується крива, залежить від необхідної точності. У випадку

різкої зміни поширення лінії використання цієї процеду

102

ност

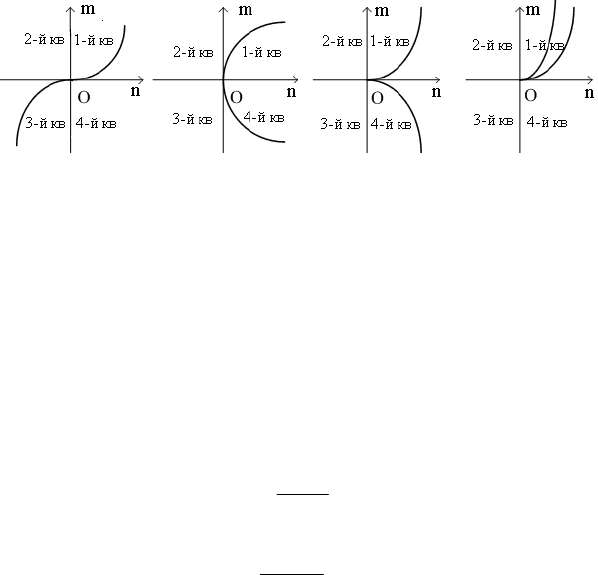
Якщо скористатися локальною системою координат, початком

якої є точка О, то з прикладів форми кривої, наведених на рис. 3.8, ви-

пливає, що ця крива може мати особливі або синг

гину, повороту першого роду або повороту другого роду. Тому для

відновлення неперервної контурної лінії необхідно виконати апрок-

ац у

могою кругової апроксимації залежно

від фор с ої.

і. Можливий і інший випадок, коли апроксимація взагалі немож-

лива, якщо масив точок заданих на площині, містить декілька з них,

розташованих на одній вертикальній прямій [141].

улярні точки пере-

сим ію контурної лінії в межах особливих точок та уточнити форм

лінії в околі таких точок за допо

ми амої крив

a) б) в) г)

Рис. 3.8. Сингулярні точки кривої:

а – точка перегину; б, в – точки повороту першого роду;

В робо ервного кон-

туру, який використовує особливі та крайові точки об’єкта, субпіксел-

і коорди

ї в визначення форми кривих в околі

собливих точок скористаємося кінцево-різницевими формулами зна-

ходження перш

– першої

г – точка повороту другого роду

ті запропоновано метод відновлення непер

н нати як вузлові точки, орієнтацію контуру, а також форму

криво околі особливої точки. Для

ої й другої похідних [152, 172]:

похідної для правої крайової точки

()

−

′

; (3.5)

−

– першої похідної для лівої крайової точки

()

−

′

−

; (3.6)

– центральна формула для першої похідної

103

()

210

2mmm

−

′

−

; (3.7)

– другої похідної для правої крайової точки

()

()()

210

2110

2mmm

nnnn

−

′′

−−

; (3.8)

– другої похідної для лівої крайової точки

()

()( )

112

jjj

ii i i

mmm

nn n n

−−

−−−

−

′′

−−

; (3.9)

– центральна формула для другої похідної

()

()()

210

mmym

2110

nnnn

−

′′

. (3.10)

−−

Якщо в околі особливих точок перші й другі похідні відповідають

умові

0 (1-й квадрант) і

() ()

'0;''fn fn><

(

)

(

)

'0;''fn fn 0

наведена на рис. 3.8

(4-й квад-

рант), форма кривої, що б, якщо –

квадрант) і

то приймається

()

'0;''0fn>> (1-й

()

(

)

(

)

;''0fn'0fn

< (4-й

на рис. 3.8в

квадрант), то

кривої, що , якщо –

рис. 3.8г.

квад-

ратів для кожної ві их випадків. Крім

цього, при виконанні умови, яка відповідає першому випадку

(рис. 3

контуру;

– точок;

– виконання апроксимації контуру

– уточнення контуру в околі крайових

повідаю м виконання круго-

вої апроксимації.

Орієнтацію контурної лінії в точ

могою ідно з

приймається форма наведена

() ()

'0;''0fn fn>> то приймається форма кривої, що наведена на

Відновлення кривої здійснюється за методом найменших

тки окремо для всіх вищенаведен

.8б), для уточнення форми кривої додатково здійснюється

кругова апроксимація.

Таким чином, метод відновлення неперервного контуру включає

такі кроки:

– визначення субпікселних координат об’єкта;

– визначення крайових і особливих точок

визначення форми кривої в околі особливих

;

або особливих точок, що від-

ть точкам повороту першого роду, шляхо

ці

(, )nm

визначають за допо-

кута між дотичною в даній точці і віссю

зг

104

(, )

nm arctg

⎛

⎜

⎝⎠

де

⎞

⎟

, (3.11)

– субпікселні зміщення контуру відносно центра піксела

n,m.

цію кривої в точках

повороту кривої за допо-

могою субпікселних зміщень наведена на ри

Виходячи записати систему рі-

внянь:

Це дає змогу виконати кругову апроксима

першого роду. Схема кругової апроксимації

с. 3.9.

з подібності трикутників можна

011

δδ

−+

⎪

де

,, ,

iji j

;

δδ

−+

⎧

−+

⎪

⎨

⎩

, (3.12)

δ δδ δ

–

субпікселні

зміщення

межі

контуру

відно

лів, відповідно;

,, ,

iji j

nmn m

– субпікселні координати

сусідніх точок, від

сно

центрів піксе

межі

повідно.

Рис. 3.9. Формування лінії при різкій зміні кривої

інії, які визначають як

У результаті розв’язування системи (3.12) знайдемо координати

центра кривизни

105

11 1 1 1

;

ij+

()

ii j j iji i

ji i j

mmn n

δδ δδ δδ

δδ δδ

++ + +

−+ −

⎧

⎪

−

⎪

−

⎩

1111 1

()

jj i i j ji jij

nn m m

δδ δδ δδ

++++ +

⎨

−+ −

⎪

(3.13)

Радіус цієї кривизни

()( )

ii j j

Rnn mm

=−++−+. (3.14)

У результаті переходу до нової координатної сітки для кожної

координати

визначимо відповідну координату:

(

jn in

mmRnn

=± −− ,)2

де і

(3.15)

[, ]

in i i

nnn

⊆

1j j+

Якщо

11ijij

[, ]

mmm

⊆

δδδ

⋅=⋅ , то крива лінія трансформується в пряму,

яка проходить через дві точки з координатами

(),( )

ii j j

, і

має вигляд:

11 1 1

(( ))(

()

in i i j j j j

jn j j

nn mm

)

δδ

++++ +

−

+−+

=++

−

. (3.16)

Для підтвердження роботи запропонованого підходу проведене

моделювання за допомогою геометричних фігур відомих розмірів. У

цьому випадку наведені дослідження фрагменту контура, зображення

якого формувалося на екрані монітора з радіусом не більше 20 пікселів

та записувалося на цифрову відеокамеру. Відстань між монітором і віде-

окамерою вибиралася таким чином, щоб відношення розміру піксела

монітора до розміру піксела відеокамери було відоме і складало 5:2.

У контур-

ної лінії б нованого

методу

ртого ступеня, оскільки фун-

кції регресії створюють криві з мінімальним відхиленням від експери-

ментального набору даних [171].

пам’яті комп’ютера формувалися два масиви даних

ез і з попередньою фільтрацією на основі запропо

. В результаті обробки отриманих координат виконувалася ап-

роксимація на основі вбудованих функцій регресії (regress) в пакеті

Mathcad з використанням полінома четве

106

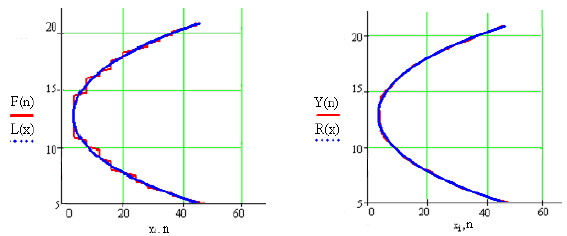
Отримані результати апроксимації контурної лінії до та після

попередньої обробки наведені на рис. 3.10.

Рис. 3.10. Позиції лінії кривої до та після апроксимації даних:

а ; б попередньої фільтрації

Відмінність координат

позицій кривих цих графіків складає від

0,01 до ікселної шир

радіус), а також

змірів об’єкта та зображення розрахована відносна по-

ювання даної кривої лінії, що не перевищує 0,04%.

3.3. Метод визначення субпікселної координати

дів

визнач

інтенсивності в околі цієї точки. Ви-

браний параметр є малочутливим до шуму та має високий рівень зава-

– відеокамери –

0,05 п ини в різних точках.

Знаючи параметри досліджуваної кривої (її ві-

дношення ро

хибка позиці

максимуму інтенсивності світлової плями

У розділі 2 наведена математична модель знаходження поло-

ження максимуму інтенсивності світлової плями (2.34). У випадку

присутності шумів знаходження максимуму ускладнюється, оскільки

розподіл інтенсивності будь-якої плями в площині матричного фотоп-

риймача має випадковий характер, а використання відомих мето

ення піку світлової плями при цьому призведе до збільшення

похибки. У такому випадку для мінімізації похибки необхідно вико-

ристати адаптивний низькочастотний фільтр, що не змінює параметри

розподілу інтенсивності в околі піксела, що має максимальну інтенси-

вність.

Основним параметром, що характеризує максимум світлової

плями, вибрано нахил розподілу

107

достійк

іцієнтами фільтра, але й

розмірністю вікна, слабо змінює нахил розподілу інтенсивності в око-

лі піксела з максимальною інтенсивністю .

Дослідження показали, що для збереження розподілу інтенси-

вності в околі піку світлової плями розмірність вікна повинна вибира-

тися, виходячи з параметрів плями, на рівні 0,5 її інтенсивності [56,

152, 169, 218].

Схема методу визначення максимуму інтенсивності світлової

плями наведена на рис. 3.11.

Алгоритм запропонованого методу визначення субпікселної

координати максимуму

лі (2.34)

–

знаходження світлової

плями згід

–

вик ку світлової

лями по

ості, оскільки при виконанні низькочастотної фільтрації з ви-

значеними апріорно не тільки ваговими коеф

світлової плями на основі математичної моде-

кі кроки: передбачає та

–

реєстрацію зображення;

вияв ;

–

визначення параметрів шуму;

–

створення низькочастотного фільтра;

лення піксела з максимальною інтенсивністю

–

виконання низькочастотної фільтрації;

–

визначення інтенсивності пікселів, що знаходяться зліва та

справа від піксела з максимальною інтенсивністю;

координати максимуму інтенсивності

но з (2.34 ) ;

онання аналогічних процедур знаходження пі

п іншій осі.

Рис. 3.11. Схема методу визначення максимуму інтенсивності

світлової плями

Максимум інтенсивності в поперечному перерізі підсвіченої

лінії за аналогією світловою плямою також залежить від нахилу фу-

нкції розподілу, тому цей метод є універсальним і може бути застосо-

ваний для визначення субпікселних координат світлової лінії. На рис.

зі

108

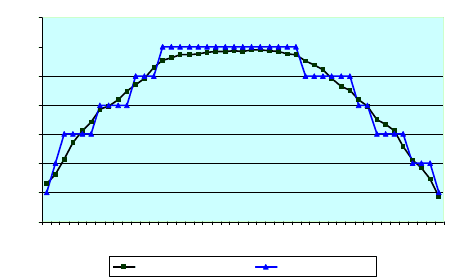
3.12 наведений фрагмент світлової лінії частини кола, отриманої в ре-

зультаті рєстрації відеокамерою до та після знаходження субпікселних

координат аналогічно з методикою, описаною в підпункті 3.2.

1 3 5 7 9111315171921232527293133353739414345

Субпікселна обробка Дані відеокамери

у точність визначення

кривої в результаті

методів виділення контурів, оскільки для бага-

тьох систем технічного зору виділення контрастних перепадів є одні-

єю з головних задач розпізнавання зображень. Це пов’язано з інтуїти-

вним розумінням того, що в контурних лініях міститься велика кіль-

кість інформації.

Контурні лінії утворюються в примежових ділянках об'єктів і

мож іж

зображеннями різних об'єк зображеннями суміжних

поверхонь одного й того ж об'єкта [3, 7, 51]. Крім цього, виділення ко-

нтурів

Рис. 3.12. Фрагмент світлової лінії

Результати обробки свідчать про висок

координат, оскільки похибка позицій координат

обробки не первищує 0,2 пікселної ширини.

3.4. Метод виділення контуру об’єкта вимірювання

У сучасній теорії цифрової обробки зображень приділяють ве-

лику увагу розробці

уть бути краями не тільки між об'єктами сцени й фону, але й м

тів і навіть між

є основою алгоритмів сегментації, які ґрунтуються на одній з

двох базових властивостей сигналу інтенсивності: розривності та од-

норідності.

109