Білинський, Й.Й. Методи обробки зображень в комп’ютеризованих оптико-електронних системах: монографія

Подождите немного. Документ загружается.

вило, к

ош рення. У зв’язку з чим більш прави-

льним

очка. ькочастотний

метод знаходження крайової точки дозволяє визначати положення краю

в міжпікселному просторі, то це дає змогу формувати контур подвійної

ширини з пікселів, знаходяться в околі крайово

Зображення, контур якого виділений за допомогою запропоно-

ваного

а також для порівняння на

ис. 3.20в – зображення, отримане детектором Канні.

райова точка знаходиться в міжпікселному просторі. Окрім цього

внаслідок впливу шуму пряма лінія формується з багатьма відхилення-

ми від свого прямолінійного п и

було б виконувати виділення контуру за допомогою двох піксе-

лів, між якими знаходиться крайова т Оскільки низ

що ї точки.

детектора наведене на рис. 3.20а. На рис 3.20б наведене конту-

рне зображення, отримане ізотропним детектором одиничної ширини

лінії, на рис 3.20г – подвійної ширини лінії,

Рис. 3.20. Виділені контури об’єкта:

а – вхідне зображення; б – ізотропним детектором з одиничною ши-

риною лінії; в – детектором контуру Канні; г – ізотропним

детектором з подвійною шириною лінії контуру

120

Ізотропний детектор аналогічно градієнтному зберігає кутові

точки та дрібні деталі зображення на відміну від детектора Канні. При

цьому, детектор, що використовує подвійну ширину лінії, забезпечує

більш високу стійкість роботи, оскільки шум на зображенні набагато

менше впливає на положення контурної лінії тому, що крайова точка

знаходиться в міжпікселному просторі.

Таким чином, ізотропний детектор виділення контуру перед-

бачає т

–

отримання бінарного зображення точок перетину вхідного та

фільтрованого зображень;

–

визначення градієнта у спільних точках фільтрованих зобра-

жень;

–

встановлення подібності пікселів, що вважаються контурни-

ми шляхом встановлення порога L та мінімального порога E ;

–

усунення несправжніх контурів;

–

оконтурювання зображення об’єкта лінією одиничної або

подвійної ширини.

Ізотропний детектор виділення контуру дає змогу отримати

стоншений контур у випадку використання лінії одиничної ширини,

зберегти контури кутових точок і контури дрібних елементів зобра-

ження.

При цьому відгук детектора (інтенсивність лінії) вищий в по-

рівнянні з детектором Канні.

Швидкодія детектора з контурною лінією одиничної ширини

вища в порівнянні з детектором, що використовує лінію подвійної

ширини, оскільки передбачена додаткова операція знаходження по-

ложення краю в , який піксел є

акі основні кроки [198]:

–

реєстрацію зображення;

–

виконання низькочастотної просторової фільтрації;

–

повторне виконання низькочастотної фільтрації (розміри фі-

льтра задаються);

міжпікселному просторі, яка визначає

онтурним.

121

3.5. Метод порогової обробки на основі

низькочастотної фільтрації

Порогове перетворення займає центральне місце в прикладних

задачах сегментації зображення, оскільки значна частина задач оброб-

ки пов’язана з перетворенням півтонових зображень у бінарні. Бінари-

зація є

оелементних перетворень спеціальних

дне для зменшення інформаційної

надмірності якого залишається лише та ін-

, напри-

або порогова обробка півтонового зображення по-

кладами застосування порогової обробки є

тобто за

інтенсивності, що розділяє

у. Аналогічний підхід можна застосувати при ная-

вності

ерший – базується на апроксимації ділянки гістограми між

піками

розподілу ймовірностей інте-

нсивно

можливість неправильного вибору порогового

локальний максимум і локальний мінімум можуть

окремим випадком препарування [186]. Операції препарування

здійснюються за допомогою п

видів. Таке перетворення необхі

зображення, в результаті

формація, яка потрібна для вирішення конкретного завдання

клад, для контуризації об'єктів.

Бінаризація

лягає в розподілі зображення на два класи за ознакою інтенсивності –

об'єкт і фон. Типовими при

машинописний текст, креслення, медичні проби під мікроскопом і т.д.

В такому випадку, використовуючи лише одну властивість –

рівень інтенсивності, можна отримати сегментацію зображення [187–

191]. При цьому об’єкти та фон повинні утворювати кластери в прос-

торі рівнів інтенсивності. За допомогою розбиття гістограми,

допомогою вибору порога значень рівня

піки, можна досягнути розділення елементів, які належать об’єкту й

ті, що належать фон

декількох видів різних областей інтенсивності. Таким чином,

основною проблемою в таких задачах є вибір порога бінаризації.

Існують декілька основних методів порогової обробки зобра-

жень. П

будь-якої гладкої функції. Другий метод полягає в тому, щоб

підібрати моделі окремо для щільності

сті об'єкта та фону. Тоді можна здійснити апроксимацію гіс-

тограми сумою щільності ймовірностей. Після оцінки параметрів

можна вибрати поріг відповідно до принципу максимальної правдо-

подібності.

Основними недоліками вищенаведених методів є складність

апроксимації, а також

значення, оскільки

122

бути рознесені нє значення

порога, що дає набли ображення об’єктів,

о знаходяться на стаціонарному фоні, мають, як правило, гістограму

у вигл

по гістограмі. Тоді визначають деяке серед

жене значення [1, 192–194]. З

яді двох вузьких піків, що відповідають щільностям розподілу

ймовірностей інтенсивності об'єкта та фону (рис. 3.21а). Значення по-

рога в такому випадку відповідає будь-якому значенню інтенсивності,

що знаходиться між піками. Оскільки зображення може мати шум і

нерівномірний розподіл інтенсивності як по фону, так і по об’єкту, то

вибір порога ускладнюється в результаті розмивання функції щільнос-

ті розподілу ймовірностей.

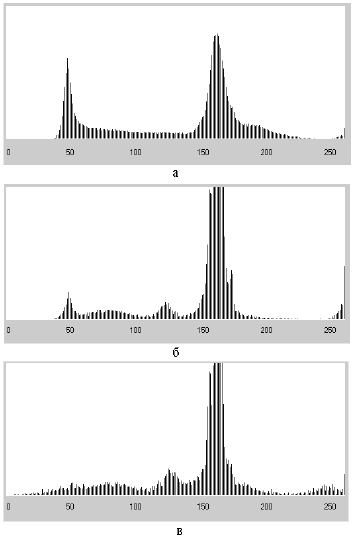
Рис. 3. 21. Гістограми зображення препарату крові

а – двопікова гістограма вхідного зображення;

б – трипікова гістограма точок перетину вхідного

та згладженого зображень; в – трипікова гістограма точок

перетину вхідного та згладженого зображень з шумом

123

Для вибору порогового значення як допоміжної ознаки може

бути взятий рівень інтенсивності, на якому знаходиться межа об’єкта.

Цьому рівню відповідає інтенсивність піксела, в околі якого знахо-

диться спільна точка фільтрованих зображень. Виходячи з вищеска-

заного, в роботі запропоновано метод автоматичного визначення по-

рога бінаризації, який оснований на знаходженні інтенсивності, що

відповідає спільним точкам фільтрованих зображень внаслідок низь-

кочастотної фільтрації.

3.5.1. Автоматичне визначення порога бінаризації на основі

трипікової гістограми

Поріг бінаризації визначається за допомогою особливого типу

гістограми, яка являє собою щільність розподілу ймовірностей інтен-

сивності спільних точок вхідного зображення та зображення, отрима-

ного в результаті низькочастотної фільтрації [195, 196].

Схема отримання зображень, фільтрованих за допомогою ни-

зькочастотних фільтрів, аналогічна схемі методу виділення контуру.

Після чого будується дана гістограма.

Гістограма щільності розподілу ймовірностей інтенсивності

спільних точок вхідного зображення та зображення, отриманого в ре-

зультаті низькочастотної фільтрації, наведена на рис. 3.21б. Гістогра-

ма цього ж зображення, але з накладеним адитивним шумом, наведена

на рис. 3.21в. Така гістограма має не два основних піки фону й

об’єкта, а три. Це піки щільності розподілу ймовірностей інтенсивнос-

ті точок перетину вхідного та фільтрованого зображення, що мають

інтенсивність вищу та нижчу, ніж значення порога, а також середній

пік, що відповідає значенню інтенсивності контуру об’єкта. Максима-

льне значення середнього піку може бути прийняте як порогове

Форма гістограми розмита за рахунок розкиду інтенсивності,

але значення щільності розподілу ймовірностей інтенсивності серед-

нього пік ої фільт-

рації [315]. осягається

можливіст ає змогу

викона з ви-

разом

(, )lInm=

у залишилось незмінним внаслідок низькочастотн

У результаті апроксимації ділянки гістограми д

ь автоматично визначити поріг бінаризації. Це д

ти поелементне перетворення інтенсивності зрізу згідно

124

1(,);

(, )

0(,),

при fnm l

gnm

при fnm l

⎧

≥

⎪

⎨

⎪

⎩

(3.26)

та отримати бінарне зображення за ознакою інтенсивності – об’єкт і фон.

Таким чином, запропонований метод порогової обробки перед-

бачає такі кроки:

–

реєстрацію зображення;

–

побудову безперервної функції інтенсивності світлового си-

гналу.

–

виконання просторової фільтрації за допомогою відповідної

маски;

–

побудову трипікової гістограми щільності розподілу ймовірно-

стей інтенсивності точок перетину вхідного та фільтрованого зображень;

–

знаходження максимального значення середнього піку в ре-

зультаті апроксимації ділянки гістограми, яке приймається за порогове;

–

виконання бінаризації на основі поелементного перетворен-

ня вхідного зображення.

Зображення препарату крові, бінаризоване та контурне, отри-

мані за

бути безпосередньо усунуті з використанням процедури знахо-

дження

ть стаціонарний фон.

допомогою автоматичного визначення порога на основі трипі-

кової гістограми наведені на рис. 3.22 [197].

Запропонований метод порогової обробки дозволяє застосову-

вати його не тільки для бінаризації, але й для виділення контуру, який

буде розглянутий нижче.

Наведені зображення препарату крові, на які накладався шум

з наступною бінаризацією та контуризацією, наочно свідчать про ви-

сокий рівень завадостійкості методу, оскільки, при наявності зашум-

леного зображення інтенсивність середнього піка його гістограми за-

лишається практично незмінним (рис. 3.21б і в). При цьому одиничні

піксели, що зберігаються після виконання операції виділення, можуть

точки згідно з виразом (1.6).

Ефективність алгоритму при збільшенні розмірів зображення

зменшується, оскільки висота середнього піка може бути недостат-

ньою для його визначення на фоні загального рівня. Це означає, що

такий алгоритм бінаризації може бути використаний для обробки

тільки малорозмірних зображень або локальних частин зображення,

які маю

125

3.5.2. Градієнтний метод автоматичного визначення порога

бінариз і однопікової гістограми

ації на основ

Для підвищення точності визначення порога бінаризації запро

поновано градієнтний метод автоматичного визначення порога біна-

ризації.

Рис. 3.22. Результати порогової обробки зображення препарату крові:

а – вхідне, бінарне й контурне, відповідно;

б – вхідне з 10%-м шумом, бінарне й контурне, відповідно;

в – вхідне з 20%-м шумом, бінар

зації [85].

не й контурне, відповідно

Встановлено, що в контурних точках значення градієнта є най-

вищим, а елементи зображення, у яких модуль градієнта малий, ле-

жать всередині об’єкта або фону. Таким чином, використовуючи до-

даткову ознаку (значення градієнта) запропоновано метод автоматич-

ного визначення порога бінари

126

Суть градієнтного методу автоматичного визначення порога

полягає у формуванні гістограми щільності розподілу ймовірностей

інтенси

значення градієнтного порога. Оскільки значення градієнта

в точках, що відносяться до контурних, завжди вища, ніж в точках

фону або зображення, то гістограма суттєво змінює свою форму. І при

збільшенні цього порога відсікається більша частина гістограми, що

призводить до зміни її вигляду від традиційної, що має два піки: фону

та об’єкта; до чітко вираженої однопікової.

У роботі [198–200] запропоновано фотометричний метод безконта-

ктного вимірювання об’єму круглих лісоматеріалів. Суть методу по-

лягає у вимірюванні площі торців колод шляхом порогової обробки

зображень торців. При цьому виконувалася порогова обробка відомим

методом згладжування гістограми та знаходження порога. Але гістог-

рама зображення торця колоди, яка наведена на рис. 3.23а, не дозволяє

визначити точно значення порога бінаризації, оскільки не виражений

пік щільності ймовірності інтенсивності об’єкта внаслідок неоднорід-

ності торця за рахунок нерівномірності зрізу та наявності кори.

Однопікова гістограма зображення торця колоди наведена на

рис. 3.23б.

Оскільки фон таких препаратів вважається стаціонарним, то

перетворення виконувалось за допомогою одного порога, значення

якого отримано на підставі гістограми. Гістограма має окрім одного

піка декілька нижчих, які можуть використовуватися як локальні по-

роги, що дає змогу підвищити точність бінаризації в цілому.

Таким чином, використання однопікової гістограми дає змогу

На рис його бінарне

зобра рога

бінари

вності спільних точок вхідного зображення та зображення,

отриманого в результаті низькочастотної фільтрації з використанням

заданого

підвищити точність, а отже й шукану площу торця колоди.

. 3.24а і б наведені зображення колоди та

ження, отримане внаслідок автоматичного визначення по

зації на основі однопікової гістограми.

Основною перевагою автоматичного визначення порога біна-

ризації на основі однопікової гістограми є невеликий час обробки,

оскільки цей алгоритм не вимагає повторного згладження зображення

для отримання вираженого піка.

127

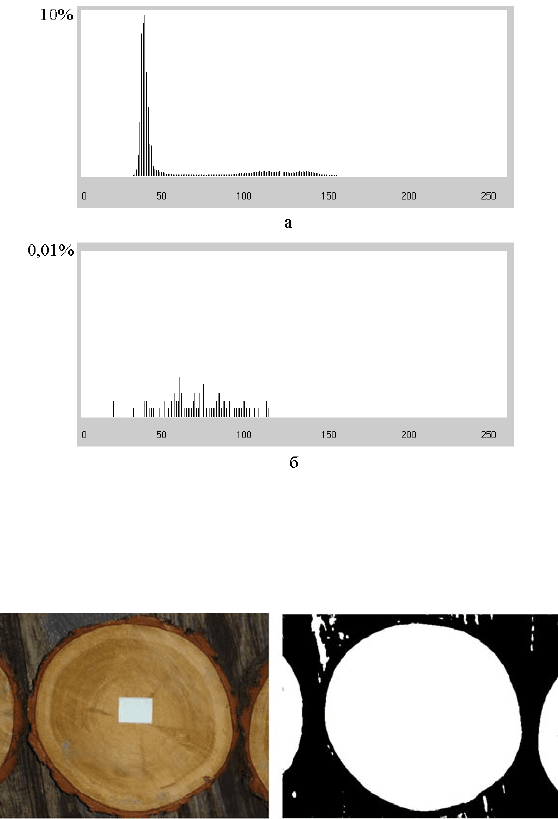
Рис. 3.23. Гістограми зображення торця колоди:

а – традиційна гістограма;

б – градієнтна гістограма фільтрованих зображень

а б

Рис. 3.24. Виділення контуру торця колоди:

а – вхідне;

б – бінарне зображення

128

Фрагменти, у вікно яких попадає край об’єкта, дають чітко

виражену однопікову гістограму, а фрагменти, що містять фон або

об’єкт у результаті низькочастотної фільтрації дають нульове або рі-

вномірне по всій гістограмі значення щільності розподілу ймовірнос-

тей інтенсивності.

Таким чином, гістограмний метод автоматичного визначення

порога бінаризації передбачає:

–

реєстрацію зображення;

–

побудову безперервної функції інтенсивності світлового си-

гналу;

–

виконання просторової фільтрації за допомогою відповідної

маски;

–

встановлення деякого значення градієнтного порога;

–

побудову гістограми щільності розподілу ймовірностей інте-

нсивності точок перетину вхідного та фільтрованого зображень;

–

знаходження значення максимального піка в результаті ап-

роксимації ділянки гістограми, яке приймається за порогове;

–

виконання бінаризації на основі поелементного перетворен-

ня зображення.

Важ ість робо-

ти при обробці слабо кож зображень, для

яких необ му його

застосування є досить перспективним особливо в медико-біологічних

дослідженнях.

3.5.3. Метод порогового виділення контуру

Автоматичне визначення порога бінаризації зображення дозво-

лило запропонувати метод порогового виділення контуру [81, 296].

Оскільки для зображення зі стаціонарним фоном або для фраг-

мента зображення досягається можливість автоматично визначити по-

ріг , то, використовуючи процедуру типу

ливою перевагою цього підходу є його ефективн

контрастних зображень, а та

хідно застосовувати змінний поріг бінаризації. То

(, )lInm=

(, )

gnm

, (3.27)

що відповідає поелементному ню, можна отримати виділе-

ний контурний препара

перетворен

129