Большаков В.Д., Гайдаев П.А. Теория математической обработки геодезических измерений
Подождите немного. Документ загружается.


ТЕОРИЯ
ТИЧЕСКОЙ ОБРАБОТКИ
ГЕОДЕЗИЧЕСКИХ
ИЗМЕРЕНИЙ

УДК 528.1 (075.8)
Большаков В. Д., Гайдаев П. А. Теория математической обра-
ботки геодезических пзмерешш. Изд. 2, перс-раб.
н
доп. М., «Недра»,
1977. 367 с.
Кинга состоит из двух частей. Первая часть — «Теория оши-
бок измерений» — включает элементы теории вероятностей и мате-
матической статистики (главы 1 и II), основы теории ошибок из-
мерений (глава III) и вопросы математической обработки много-
кратных измерений одпой величины (глава IV). Вторая часть —
«Метод наименьших квадратов» — освещает сущность этого метода
(глава V), основные н видоизменсипые способы уравнивания ре-
зультатов измерений нескольких величин с освещением вопросов
оценки точности (главы VI—VIII). Рассматриваются вопросы интер-
полирования измеренных значений неизвестной функции (глава IX)
и уравнительных вычислений при большом числе неизвествых
(глава X). Приведенные в книге способы и схемы вычислений для
обработки геодезических измерений иллюстрируются примерами.
В приложении даны вспомогательные таблицы, необходимые для
расчетов точности.
Табл. 67 + 7 прпл., ил. 16, список лпт. — 63 назв.
В
20701
~052
043 (01)—77
57
~
77
© Издательство «Недра», 1977

и I НЬДАКТОРОВ
ПЕРВОГО ИЗДАНИЯ
Труд П. Л. Гайдаева к 13. Д. Большакова «Теория математиче-
ской обработки геодезических измерении» соответствует дисциплине,
называвшейся ранее в учебной литературе «Способ наименьших
квадратов^. Новое пазвание точнее отражает содсржаппе труда и
учебной дисциплины.
Книга соответствует современному состоянию данной научиой
ДИСЦИПЛИНЫ М по содержанию существенно отличается от раиее издан-
ных аналогичных учебников.
В книге изложепию основного учебного материала предпосланы
необходимые сведения из теории вероятностей и математической
статистики, причем эти сведения используются как исходное матема-
тическое основание для изложения теории ошибок измерении и .метода
наименьших квадратов.
Вопросы классификации измерений и уравнительных вычислений
изложены на новой методологической основе, в которой отсутствует
разделение измерений па «непосредственные», «посредственные» и
«условные», на чем основывалось изложение способов решения задачи
уравнивания во многих учебниках п что весьма затрудняло изучение
столь лажной для ипженера-геодезиста научной дисциплины. Такой
методологический подход позволил устранить существовавший раз-
рыв в изложении основных способов решения задачи уравнивания*
трактовавшихся как «способ посредственных измерений» и «снособ
условных измерений». В книге для обоих способов дастся нх общая
теория (глава V), базирующаяся на избыточных измерениях, что со-
ответствует действительному порядку вещей при постановке п реше-
нии задачи уравнивания.
Кроме основных способов уравнивания (главы V—VI), в книге
излагаются видоизмененные способы — параметрический способ с из-
быточными неизвестными, снособ условий с дополнительными (не-
измеренными) неизвестными и др. (глава VIII). Изложение всех
способов уравнивания сопровождается тщательно и полно отработан-
ными примерами.
1* 3

Важный для геодезических работ вопрос оценкп точности изме-
рений базируется на принятом авторами положении, что математиче-
ское ожидание для ошибок измсрсплй отличается от дуля, а следова-
тельно. и предельное значеппе среднего арифметического отличается
от истинного значения измеренной величины по причине влияния
систематических ошибок. В книге приведены рекомендации но
борьбе с систематическими ошибками, являющимися в современных
высокоточных измерениях основным препятствием для существенного
повышения точности геодезических определении (главы III. IV и др.).
В отличие от записи алгоритма Гаусса, связанной с порядковым
номером букв в латинском алфавите, в книге прпмепястся запись,
в которой коэффициенты уравнений обозначаются только буквами а
(для пеходион системы) и Л
г
(для преобразованных систем) с цифро-
выми индексами.
В книге с достаточной для учебника полнотой освещается вопрос
уравнительных вычислепин при большом числе неизвестных (глава X),
имеющий важпое значение для вычисления государственных геоде-
зических сетей высших классов»
Математические сведения, необходимые для изучення дисциплины,
пе выходяг за рамки оспов дифференциального п интегрального ис-
числений. В теоретических выводах там, где ото было целесообразно,
пепользовались элементарные сведепяя из матричного исчисления.
Б. С. Кузьмин, В. Е. Гмурман

ПРЕДИСЛОВИЕ
Но содержанию дашшй учебник соответствует программе курса
«Теория математической обработки геодезических измерении» для гео-
дезических вузов п факультетов. Программа одобрена на заседаниях
кафедры геодезии Московского института инженеров геодезии, аэро-
фотосъемки и картографии (МИИГАиК) и кафедры геодезии и астро-
номии Военно-ипжеиерпой Краснознаменной и ордепа Ленина акаде-
мии им. В. В. Куйбышева н утверждена Учсбпо-методнческим упра-
влением по высшим учебным заведениям Министерства высшего и
среднего специального образования СССР. Учебник предназначен
для студентов вторых и третьих курсов очного, заочного и вечернего
обучепия геодезического, аэрофотогеодезического и картографиче-
ского факультетов геодезических вузов и соответствующих^снениаль-
ностей нсгсодезическнх вузов.
При изложении учебного материала КНИГИ используется мате-
матический аппарат, в основпом известный студенту 2-го курса тех-
нического вуза. Однако то обстоятельство, что данный курс изу-
чается параллельно с курсом высшей математики, создает некоторые
трудности п должно учитываться лектором. Что касается понятий
из специальных дисциплин (геодезии и др.), используемых ири из-
ложении учебного материала курса, то они не создадут особых за-
труднений студентам, изучившим первую часть курса геодезии, и
лишь в незначительной своей части потребуют некоторых дополни-
тельных пояснений.
Во втором издании киши «Теория математической обработки гео-
дезических измерений» заново наиисаи § 52 «Допуски для результа-
тов измерении и их фупкцпй» с учетом развития взглядов па эти
важные для геодезии вопросы. В остальном содержание книги под-
верглось коррективам, связанным с устранением неточностей.
Изложение теоретического материала в книге, как правило, ил-
люстрируется примерами. Можно надеяться, что ото позволит
использовать учебник не только для обучения студентов, но и в
тонографо-геодезнческом производстве.
о

Что касается степейи участия авторов в создании учебника, то
все его главы написаны ири тесиом и полном сотрудничестве ав-
чоров; поэтому оба автора в равной мере ответственны перед чита-
телями за все содержание книги.
Авторы благодарны коллективам кафедры геодезии МИИГАпЬ*
и кафедры геодезии п астрономии академии им. В. В. Куйбышева
за помощь и полезные советы при работе пад программой курса
и рукописью учебника.
Отзывы и критические замечания читателей книги авторами бу-
дут восприняты с должным випманпем.

ВВЕДЕНИЕ
Измерения играют весьма важную роль во всех областях техники,
они доставляют исходную информацию для точных наук.
Измерения составляют основное содержание всех работ, выпол-
няемых с целью картографо-геодезического изучения земной поверх-
ности. Методы и средства измерений, связанных с изучением Земли,
разрабатываются в геодезии, практической астрономии, гравиметрии,
фотограмметрии, картометрии, космической геодезии и в других
науках.
Измереппе любой величины рассматривают с двух точек зрения:
количественной, выражающей числовое значение измеренной вели-
чины, н качественной, характеризующей точность измерения.
С развитием науки и техники, в частности геодезии, повышается
точность измерений п совершенствуются методы их математической
обработки.
В измерениях не должно быть промахов п просчетов, или, как
говорят, грубых ошибок. Для обнаружения последних в геодечиче-
ской практике всегда делают не менее двух измерений каждой вели-
чины п. кроме того, используют математические зависимости между
измеренными величинами (например, равенство суммы углов в пло-
ском треугольнике 180°. равенство нулю суммы превышений в зам-
кнутом высотном полигоне н т. п.).
Из опыта известно, что даже при самой тщательной и аккуратной
работе многократные (повторные) измерения любой постоянной вели-
чины всегда дают несколько различные результаты, а результаты
измерений математически связаипых величии образуют иевязкп *.
Порядок величины невязок и расхождений между результатами по-
вторных измерении должен соответствовать точности измерении,
что п является признаком отсутствия грубых ошибок в измере-
ниях.
То обстоятельство, что и при отсутствии грубых ошибок резуль-
таты повторных измерений всегда в известных пределах различаются
между собой, объясняется тем, что любые измерения всегда сопро-
вождаются неизбежными малыми ошибками, т. е. отклоиепиями
результатов измерении ог точных значении измеренных величин.
Источниками этих ошибок являются неточности измерительных оно-
* Если математическую зависимость между измеренными величинами выра-
зить равенством ф(А'„ . . Л'
я
) = 0, то невязка определится равенством
И*
= • • •» где х
п
— результаты пзмереппй.

раций наблюдателя, неточности изготовления и юстировки приборов,
недостатки учета влияния непрестанно изменяющихся условий из-
мерений п др.
«Поэтому их (т. е. неизбежные ошибки. — Прим, авт.) прихо-
дится терпеть в наблюдениях, во следует, но возможности, ослабить
их влияние на полученные результаты путем искусного комбиниро-
вания...» *.
В вопросе о точности измерений и их математической обработки
следует обратить внимание на одно важное обстоятельство. Но вда-
ваясь пока в способы числовой оцонкн качества результатов измере-
ний, а риог! можно утьерждать. что результаты, содержащие мень-
шие ошибки, больше импонируют потребителю этих результатов.
На этом основании иногда предъявляют явно завышенные требова-
ния к точпостн измерении,
не
соответствующие действительной необ-
ходимости и реальным возможностям. Однако излишняя точность
измерений столь же нежелательна, как и недостаточная точпость, так
как это ведет к увеличению объема и сроков работ и к их удорожа-
нию. Поэтому возникает задача определения целесообразной, т. е.
необходимой и достаточной, точности измерений и обработки их ре-
зультатов.
Нзучепием качества геодезических измерений, законов возникно-
вения н действия неизбежных малых ошибок, разработкой правил
оценки и расчетов необходимой точности измерений, а также методов
н способов вычислении, позволяющих получать при экономных за-
тратах вычислительного труда наилучшие окончательные результаты,
и занимается теория математической обработки геодезических из-
мерении.
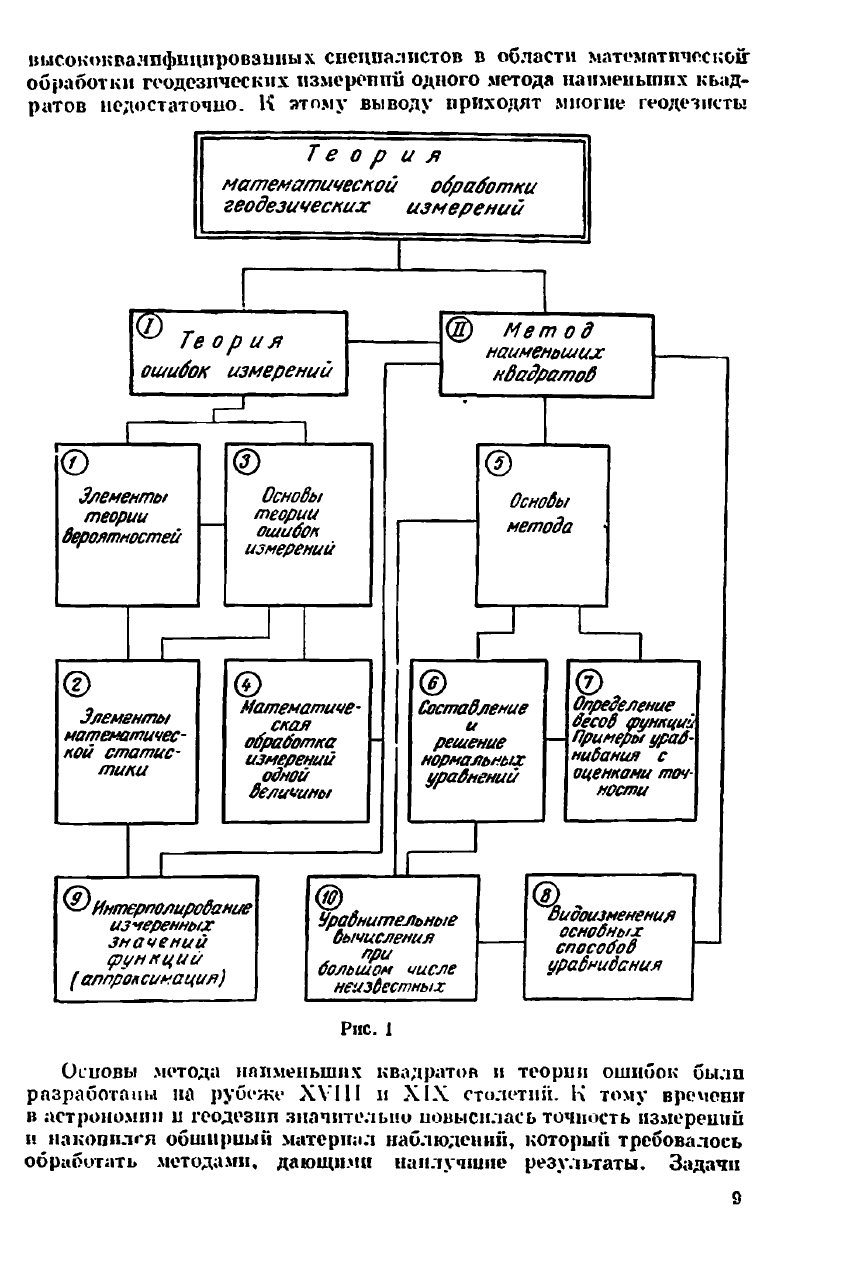
Логическая структура книги показана на рис. I; она состоит из
двух частей: теории ошибок измерении и метода наименьших квадра-
тов. Обе части основаны на элементах теории вероятностей; при
этом ладо иметь в виду, что «Теория вероятностей» как отдельный
предмет в геодезических вузах не изучается. Небольшой раздел этой
важной наук», включенный в ирограмму курса высшей математики
технических вузов, восполняет этот пробел лишь частично.
Авторы стремились учесть достижения говетской геодезической
школы в методологии и методике изложения способа на и меньших
квадратов, опираясь при этом на труды К. Ф. Гаусса (1777—1855).
Может возникнуть вопрос: почему традиционное название дис-
циплины «Способ наименьших квадратов» замешаю на «Теорию ма-
тематической обработки геодезических измерении»? Для ответа на
этот вопрос следует обратиться к схеме логической структуры книги,
откуда вытекает необходимость такой замены. Метод наименьших
квадратов, предложенный Лежвндром и Гауссом, болев чем за 160-
летний период его примепония всесторонне проверен практикой,
получил и получает все новое развитие. Тем не менее для подготовки
* К. Ф. Гаусс. Избранные сочпнеппн, т. I. М., Геодезпздат, 1957
с. 18.
II
высококвалифицированных специалистов в области математической:
обработки геодезических измерений одного метода наименьших квад-
ратов недостаточно. К атому выводу приходят многие геодезисты
Рис. 1
Основы метода наименьших квадратов и теории ошибок былп
разработаны на рубеже XVIII и XIX столетни. К тому времени
в астрономии и геодезип значительно повысилась точность измерешш
и накопился обшириый материал наблюдении, который требовалось
обработать .методами, дающими наилучшие результаты. Задачи
II

теоретической и практической астрономии и геодезии настойчиво
требовали создания научно обоснованного метода математической
обработки результатов измерений.
Отвечая требованиям науки и практики, ученые выдвипулп ряд
предложений по математической обработке результатов измерений.
В XVIII в. выдающиеся астрономы и математики того времени —
член русской Академии наук Леонард Эйлер (1707—1783), II. Ламберт
(1728—1777), П. Лаплас (1749—1827) и другие —предлагали различ-
ные способы, по все. опи не нашли применения по своей сложности.
В 1806 I. французский математик А. Лежа ид р (1752—1833) опубли-
ковал работу «Новые методы определеиня комстиых орбпт». в кото-
рой предложил зля математической обработки результатов наблюде-
ний метод наименьших квадратов. проиллюстрировав его примером
из геодезии (определение размеров Земли на основе градусных из-
мерений).
В 1809 г. Карл Гаусс (1777—1855) опубликовал свою работу
«Теория движения небесных тел. обращающихся вокруг Солнца
во коническим сечениям». В этой работе Гаусс блестяще развивает
алгебраическую сторопу метода наименьших квадратов. Достаточно
сказать, чго введенные им обозначения и символика сохраьплпсь и до
настоящего времени. Это обстоятельство позволяет считать Гаусса
наряду с Лежандром создателем метода наименьших квадратов.
В 1810 г. французский .математик н астроном Лаплас, используя
результаты Муавра (1067—1754), вывел формулу, позволяющую
определять вероятности числа появлений случайных событий при
многократных испытаниях. Эта формула значительно расширила
юзможностп прпмепения теории вероятностей в практик? и. в част-
ности, при обработке результатов паблюденнй.
Значительное развитие теория вероятностей получила в работах
русских математиков: академиков II. Л. Чебышева (1821—1894),
Л. А. Маркова (1850-1922) и А. М. Ляиупова (1857—1918).
Работы П. Л. Чебышева, А. А. Маркова н А. М. Ляпунова про-
должили и развили советские ученые: С. II. Бсрнштейн, А. Н. Колмо-
горов. А. Я. Хпнчин, II. В. Смнрпов, В. II. Романовский, Ю. В. Лип-
ник. Б. В. Гнеденко п другие, создавшие передовую советскую
школу теорпи вероятностей и математической статистики.
Широкое применение в геодезии метод наименьших квадратов
нашел лишь в середине XIX в. после выхода в свет ряда руководств
по практическому его применению. Характерно, что впервые прак-
тическое руководство по применению этого метода в геодезии было
издано в России в 1836—1837 гг. русским военным геодозистом
А. П. Болотовым. В Германия руководство такого рода было впервые
издано лпшь в 1843 г.
Разработкой методов уравнительных вычислений * занимались
главным образом астрономы п геодезисты. Из зарубежных ученых
» «У равппте л
ьпыми»"
называют вычисления, связанные с математической
обработкой пзмереипй по методу наименьших квадратов.
г,;
