Большаков В.Д., Гайдаев П.А. Теория математической обработки геодезических измерений

Подождите немного. Документ загружается.

Итак,

= (I

-204>

Теперь имеются все предпосылки для доказательства теоремы Чебышева

в нредположеппи, что рассматриваемые велпчшш попарно независимы и имеют

равномерно ограниченные (т. е. ограниченные одним и тем же числом) дисперсии,

Р 30|< е) > 1-6, (1.205)

11— ОО

где е и б — сколь угодно малые положительные числа.

Применим к случайной величине х неравенство Чебышева, полагая е = а»

Р = (1.206)

л-со

Рассматривая неравенство (1.206), убеждаемся, что как^бы малб ни было

заданное число е, всегда можно подобрать число п столь большим, чтобы соблю-

далось неравенство

О(А')

Поэтому можно иаписать

Р (|*-Х|>е)<б,

л-* оо

а переходя к противоположному событию,

Р (|х-Х|<е)>1-6,

л—со

что и требовалось доказать.

Таким образом, математическое ожидание ириблпженно можно

заменять средним зиачением пз п наблюдений и с тем бблышш осно-

ванием. чем больше число наблюдений.

2. Понятие о центральной

предельной теореме Ляпунова

Важпость закона больших чисел для практических применений

теории вероятностей очевидна. Не менее важны для нрактики тео-

ремы, объединенные общим названием «центральная предельная тео-

рема». Еслп закоп больших чисел устанавливает статистические свой-

ства среднего значения случайной величины, то центральная предель-

ная теореди! устанавливает условия, ири которых возникает

нормальный закон распределения.

Наибольший вклад в разработку этой теоремы внесли русские

математики П. Л. Чебышев, А. А. Марков и А. М. Ляпунов. Так как

строгое доказательство центральной предельной теоремы дано

А. М. Ляпуновым, то ее чаще всего называют теоремой Ляпунова.

Строгое доказательство этой теоремы требует значительного расшпре-

иия рамок даипого курса. Поэтому ограничимся лишь изложением

основной идеи этой теоремы и приведем упрощенное

ее

доказательство,

в известной мере иллюстрирующее основную идею строгого доказа-

тельства.

Сущность центрально» предельной теоремы заключается п следу-

ющем. Если некоторое случайной явление есть результат действия

достаточно большого числа независимых (пли слабо зависимых) слу-

чайных явлении, каждое из которых оказывает малое воздействие

на окончательный результат, то закоп распределения вероятностей

указанного сложного явления близок к нормальному.

Применительно к случайным величинам теорему Ляпунова можно

сформулировать так:

Если некоторая случайная величина есть

сумма достаточно большого числа других

случайных п с з а в и с н м ы х в е л и ч и н, отклоня-

ющихся от своих математических ожиданий

на весьма малые величины по сравнению

с отклонениями суммарной величппы, то за-

кон распределения этой суммарной случай-

пой в е л и ч и н ы б у д е т близок к нормальному.

Приведем упрощенно© доказательство теоремы Ляпунова для случайных

величин.

Предположим, что случайная величина Уесть сумма п независимых случай-

ных величин Х( (I = 1. - . -, п), т. е.

V = .*!+. •

+ Х

<I -207)

Представим (1.207) так

Г-И «(*, +

§,)

+ й„ + ы.

Так как _ _ _

то

Т|=!,+ . .

&П,

(1.208)

т. е. случайное отклонение суммы является суммой случайных отклонений сла-

гаемых.

Представим теперь, что'каждое перелагаемых составлено, в свою очередь,

пз некоторых элементарных слагаемых^, рапных по абсолютной величине, но

принимающих с одинаковой вероятностью знаки плюс п минус. Ввиду бесконеч-

ного разнообразия взапмвых^связей в природе такое допущение возможно, так

как каждое из слагаемых, в свою очередь, является результатом сложения мпо-

гих влиянии, н этот ход рассуждений можно вести сколь угодно долго.

Как следствие указанного упрощения, величину г| можпо представить как

сумму большого числа N элементарных слагаемых е с одинаковой вероятностью

р = 0,5, принимающих знаки плюс пли минус, т. е.

(1.209)

х-1

где |е | = сонз1, а слагаемые е различаются только знаками.

Конкретное значение случайной величины

т)

будет зависеть от числа положи-

тельных слагаемых е в данном испытании. Предположим, таких положитель-

ных слагаемых окажется к. Тогда конкретное значенпе г|

- будет

т)| =

А-1

| —

(Л'—к) | е |

(1.210)

(очевидно, что отрнцательпых слагаемых окажется при этом .V — к). Далее

получим

= к | е |-Л

|е|+А-1 е\ = 2к|е|-Л

|е | =

т. е.

=2Л'|е|(4--0.5). (,.211;

2Л'|е| — величина постоянная, а в скобках правой части равенства (1.211)

мы получили отклонение относительной частоты события от вероятности. Ио

так как отклонение относительной частоты от вероятности подчиняется нормаль-

ному закону распределения, то тем самым теорема Ляпунова доказана, разу-

меется, при тех упрощениях, которые нами сделаны в начале рассуждений.

Теорема Ляиупова л моет важное значение для теории ошибок

измерений.

Глава II

ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

§ 18. ВЫБОРОЧНЫЙ МЕТОД

Прп изложении главы I предполагалось, что законы распределе-

ния случайных величин л параметры этих закопов известны. Однако

при решении практических задач указанные допущения никогда пол-

ностью ие соблюдаются. Как правило, бывает известен лить закон

раснределепия, а его параметры определяются по результатам на-

блюдений. Иногда по результатам наблюдений приходится опреде-

лять и закоп распределения.

Обе задачи — определение закона распределения и определение

его параметров — можно решить точно, если получены из наблюде-

ний все значения случайной величины, которые называют гене-

ральной статистической совокупностью.

Однако для непрерывных случайных величин это принципиально не-

возможно, а для дискретных величин в большинстве случаев прак-

тически невозможно. Поэтому на практике применяют так называе-

мый выборочный метод. Сущность этого метода заключается в том,

что из генеральной совокупности получают лишь часть значении

или, как говорят, делают статистическую выборку и на ее основе

решают задачу. Разумеется, при этом получают приближенные

ответы.

Методами приближенного решепия вероятностных задач па ос-

нове выборки занимается математическая статистика.

Выборку стараются делать так, чтобы она распределялась равно-

мерно по геперальпой совокупности и, таким образом, паи.чучшим

образом отражала свойства случайной величниы. Приведем примеры.

Промер 1. Для определения запаса древесины на некоторой площади леса

производят выборочный обмер высоты и диаметра ствола (на высото груди)

некоторых тшигшых или средних деревьев на равномерно расположенных по

лесу площадках размером 50 X 50 м и, кроме того, подсчитывают число деревьев

на этих^площадках. В результате получают «средний» объем дреиссипы па «сред.

ней» площадке. Умножив полученный результат на где Р га—площа

Дь

всего леса, получают приближенное решение задачи. Математическая статистик,

позволяет прп этом дать и вероятностную ^оценку полученного результата.

Пример 2. Для того чтобы быстро определить распределение роста мобидц.

зованных солдат п получить па складе обмундирование с правильным соотно-

шением его размеров, выстраивают солдат но росту («по ранжиру») и делают

обмер каждого десятого в строю. Этих данных оказывается достаточно для уд

влетворптсльного решения вопроса, особепно если учтены еще и возможные

отклонения полученных статпстпческпхГнарамстров и соответственно получены

запасные комплекты.

Аналогично па основе выборок определяют урожайность злаков,

количество выпавших осадков, точность измерений и т. п.

Приближенные значения основных характеристик случайпой ве-

личины (математического ожидания и дисперсии) получают по фор-

мулам

Л/ (А") —« (11.1)

I) (А") ~ О' (А') = « (11.2)

где п — число наблюдений.

Ясно, что полученные статистические (эмпирические) параметры

распределения тем точпее, чем больше произведено наблюдений и чем

лучше сделана выборка.

Приближенная картина характера распределения случайной ве-

личины представляется «эмпирической кривой распределения». Для

построения этой кривой вычисляют по материалам выборки относи-

тельные частоты наблюденных значений случайной величины в неко-

торых йравнопромежуточных» интервалах. Далее последовательно

откладывают по оси X равные между собой интервалы изменения X

и строят на этих интервалах прямоугольники с высотами, численно

равными соответствующим относительным частотам. В результате

получают ступенчатую линию («гистограмму»). Сглаживая эту ступен-

чатую линию, получают плавную эмпирическую кривую распре-

деления.

§ 19. ДОПОЛНИТЕЛЬНЫЕ ХАРАКТЕРИСТИКИ ВЫБОРОК

1. Эксцесс

Эксцессом Е называют величину, вычисляемую по формуле

сил

В случае точного соблюдения нормального закона распределения

в выборке величина Е должна равняться пулю, что следует из со-

отношения (1.145). Для эмпирических значений 112 п ^ эксцесс, как

правило, нулю равен пе будет.

Отклонение эксцесса эмпирического распределения от его теоре-

тического значения, т. е. от нуля, указывает на отклонение эмпири-

ческого распределения от нормального, причем, если Е > О, рас-

пределение «высоковершшшое», если Е <

— «низковершинное»

(рис. 7).

Не требует пояснений утверждение, что эмпирическое распределе-

ние может точно совпасть с нормальным случайно ИЛИ при чпеле

испытаний, неограниченно большом. Таким образом, исследователь

практически всегда при вычислении эксцесса эмпирического распре-

деления получит величину, отличную о г нуля. Но можно ли считать

полученное значение эксцесса несущественным при данных усло-

виях, а следовательно, отклонение вершины кривой эмпирического

распределения от нормальной

кривой — допустимым?

Для этой цели применяют

следующую формулу, позволя-

ющую вычислять среднее квад-

ратпчоское отклонение эксцесса:

о'(Е)** (И-4)

паблюдепий

Рпс. 7

где п — число

(испытаний).

Если число наблюдении не очень велико (20 < »< оО), то экс-

цесс можпо считать несущественным при условии

(П.5)

вдесь

Е\ — абсолютное значепие эксцесса;

о' {Е) — среднее квадратическое отклонение эксцесса (эмпири-

ческое).

2. Асимметрия

В практике встречаются случаи, когда эмнирическая кривая

распределения является как бы скошенной. В качестве числовой

характеристики в этом случае применяют так называемый показа-

тель асимметрии

8к

~ (а')з'

(И.6)

где 8к — показатель асимметрии (ЗД — первые буквы слова зкетс-

ПС58 — скошепиость);

Рз — третий центральный момент;

(о')

— третья степень среднего квадратпческого отклонения (оче-

®идпо, о

= (.1; для теоретических значений).

Для симметричных распределений, каким является и нормальное,

очевидно, что теоретическое значение Зк — 0, так как суммы поло-

жительных и отрицательных кубов отклонений при вычислении и

по формуле (1.141) взапмпо компенсируются. Когда Зк окажется

больше нуля, кривая будет скошена влево, а когда Зк окажется

меньше нуля — вправо (рис. 8).

Для нормального распределения при большом числе испытании п

среднее квадратическое отклонение показателя асимметрии может

быть вычислено по эмиириче-

ской формуле

о'(Зк) ъ*

/4-

(И. 7)

Рис. 8

Если будет выполнено

условие

|5*КЗо'(5*). (Ц.8)

то эмпирическое распределение можно считать практически симмет-

ричным.

Иногда вместо показателя асимметрии 8к применяют постоянную Пирсона

Рп называемую мерой скошенности, равную

(Из)

Нетрудно установить, что

[о' (М

4 {Зк)*

\о' (Зк)]* С ((5,)

тУЦ-

Условию (11.7) аналогично условпе

|Р,|^Зо'(Р1).

Недопустимые отклонения Зк от нуля в большинстве случаев

означают наличие в результатах наблюдений односторонне действу-

ющих ошибок. Понятие одпосторопне действующих ошибок до-

ступно без дополнительных пояснений, однако к ним еще вернемся

ниже.

Пример. При исследовании светодальпомсра одна и та же линия была изме-

рена 16 раз. Пользуясь данными, помещенными в табл. 4, вычислить централь-

ные моменты ра. дисперсию В'(Х), среднее квадратическое отклонение

о', эксцесс Е, среднее квадратическое отклонение эксцесса о' (Е), асимметрию

8к и среднее квадратическое отклонение асимметрии о' (Зк). В графе «Вычис-

ление» табл. 4 приведен расчет числовых характеристик.

Как нетрудно видеть из результатов вычислений, эксцесс п

асимметрию здесь можно считать несущественными, а эмпирическое

распределение — практически нормальным.

Таблица 4

результаты пз-

нерсиий 5,-,

0994.911

890

879

895

882

898

885

883

902

901

895

894

896

883

895

902

-в

р.

мм

+17.8

-3,2

-14.2

+ 1.8

—11.2

+4,8

-8.2

-10.2

+8.8

+7,8

+ 1.8

+0,8

+2.8

—10.2

+1.8

+8.8

®8?

СР

=6994.8932

2 = -0.5

316.84

10.24

201.64

3.24

125.44

23.П/,

67.24

104,04

. 77.44

60.84

3.24

0.64

7.84

104,04

3.24

77.44

2 = ^86.4

65?

+5639.8

-32.8

—2863.3

+5.8

-1404.9

- 110.6

—551 \

-1061.2

+681,5

474.6

+ 5.8

+0.5

+22.0

-1061.2

+5.8

+6815

Вычислепие

У = +653.1

' -°-

пл.

М2

= "Тб~

-1

653

=40.8;

, _

199313

„

=124э/;

в^го:

о'

—

!^'—89 мм;

Е =

Г.

'.Я

5500

/; =

—0.74:

VI'

5А- =

(О')*

(5*)'

(5к

УбЛ'? = 199313

§ 20. ОЦЕНКА ПРИБЛИЖЕННОГО ЗНАЧЕНИЯ

МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ

Рассмотрим способы вероятностных оцепок приближенного зна-

чения математического ожидания, получаемого как средпее. т. е.

значения х. В оспову решения поставленной задачи положим метод

«доверительных интервалов». Сущность этого метода состоит в следу-

ющем.

Задаваясь «довсрительпой вероятностью» (3, определяют дове-

рительные интервалы, укладываемые в обе стороны от х (т. е.

в сторону уменьшения и

сторону увеличения), в пределах которых на-

ходится значение А с вероятностью р.

При этом рассмотрим два случая:

1-й случай: точное значение стандарта а известно.

Зная точное значение й (А

) = о

(X), получаем точное значение

дпсперсип среднего

и стандарт среднего

- ,/—~ о (X)

= (Г 1.9)

г И '

Далее рассуждаем так. Случайная величина х имеет параметры

распределения: М (х) = X и о (аг) = Вероятность того, что

У п '

конкретпое значение случайной величины попадает в интервал от

(X — 5.-) Д° № + как известно, равна

СЬ

где

§/=1*1—л

Нам задано = р и известно а (я). Пользуясь таблицами

Ф (*,) (прпл. 2), по заданному значению р находим

' °

С*)

и, накопец. — = 1

{

а (х).

Вопрос о том, какой доверительной вероятностью следует зада-

ваться, решается в каждом коикретиом случае, исходя пз тех или

иных соображений, причем субъективный подход вдесь неизбежен.

В большинстве случаев будем задаваться значением р = 0,99 и р =

= 0,68.

Строго говоря, точное значение стандарта прп обработке резуль-

татов наблюдений — абстракция. Однако оиытом установлено, что

значение стандарта можно считать практически точным, если оно

иолучепо по формуле

*'(Х)=\ п-\ (»

где л^ 20.

Формула (11.10) вытекает из формулы (П.2). Поэтому в дальней

шеи изложении будем считать, что стандарт известен практически

точно, если его значение получено пз 20 наблюдений и более.

Перейдем теперь к выводу формулы (11.2).

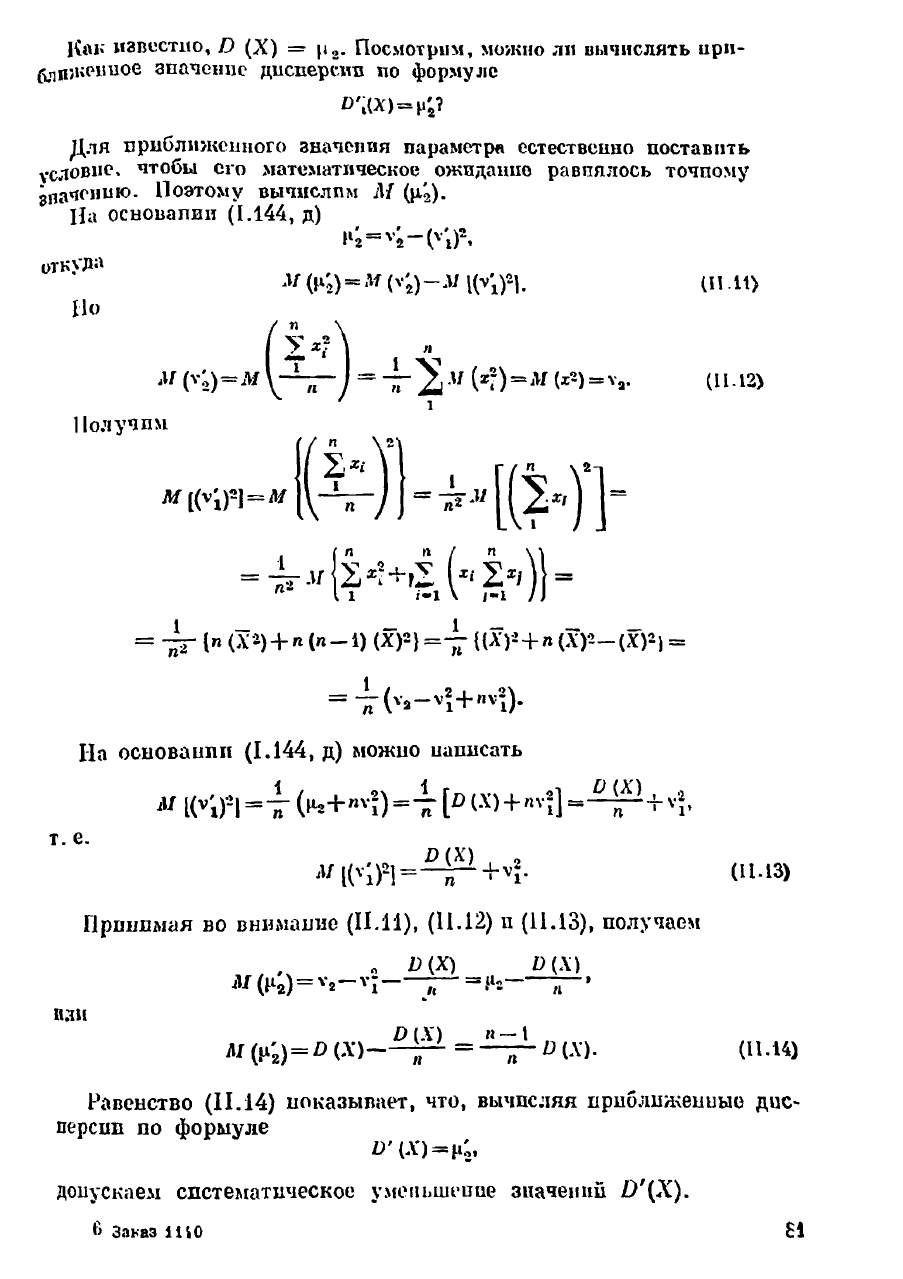
Как известно, О (X) = р

. Посмотрим, можно ли вычислять при-

ближенное значение дисперсии по формуле

Для приближенного значения параметра естествеино поставить

условие, чтобы его математическое ожидашю равнялось точному

значению. Поэтому вычислим М (ц'

Па основапии (1.144, д)

отк>"Д

(П

.11)

Но

V"» о

(11-12)

Получим

= I"

(**)

("-*) (Х)2) {(*)* +

(Х)2-(ХГ-) =

На основании (1.144, д) можно написать

т. е.

Принимая во внимание (11.11), (11.12) и (11.13), получаем

. о 1>(Х) , О(Х)

М (Н) = Ч--— =

}

и——»

(11.13)

пли

0(А")

« — I

Л/ (ц'

) = о (X) = -7Г

(А')-

(11.14)

Равенство (11.14) показывает, что, вычисляя приближенные дис-

персии по формуле

допускаем систематическое уменьшение значений 0'{Х).

6 Заказ ню 81

Из

(П. 14)

следует

V. (*,—

лт

х)=]

и —1

Поэтому приближенное значение дисперсии вычисляют но фор-

муле (11.2)

У (**-*)*

Пример 1 Случайная величина X наблюдалась 20 раз. Результаты на-

блюдений приведены в табл. 5.

Таблица 5

, 1

*<•

10,5 6 10,6

10.6

10,9

2 10,8

7 10,9

12 11.3

17 10.8

10,9 8 11,0 13

10,5

10,7

11,2

10,3 14

10,7

19 10.9

.0,4

10,8

20 11,0

Требуется найти доверительный интервал для^математпческого ожидания,

соотпетствуклщш доверительной вероятности р = 0,99.

Решение.

~ 20 "

>0,78;

2] (Ч-10.78)2

(ДГ) =

~ ПГ~ =0.004-, а' (X) =0.253,

V ~20~=0.056.

В прпл. 2 находим по 0 = Ф = о,99 значеппе

*р=2,57,

откуда

(-0

'(5 —

0,050

•

2,57 = 0.14.

• Пример зашсствован из книги Е. С. Вептцеля «Теория вероятностей».

М., «Наука», 1%9. о76 с. с пл. *