Бугай П.Т. Теорія помилок і спосіб найменших квадратів
Подождите немного. Документ загружается.

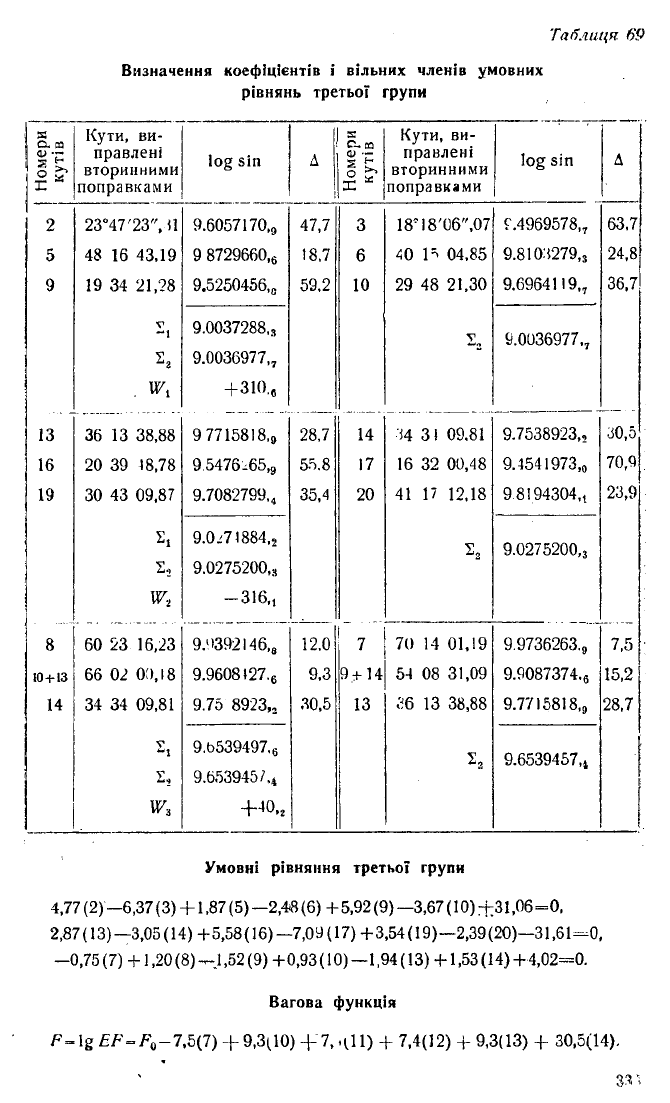
Номери
кутів
Кути, ви
правлені
вторинними
поправками
log sin
A
Номери
кутів
Кути, ви
правлені
вторинними
поправками
log sin
Д
2
23°47'23",И 9.6057170,9 47,7 3
18° 18'06",07
f.4969578,, 63,7
5 48 16 43,19
9 8729660,e
18,7
6
40 1=- 04,85
9.8103279,3 24,8
9 19 34 21,28
9.5250456,0 59,2 10 29 48 21,30
9.6964119,, 36,7
V
“1
9.0037288,3
9.0036977,7
Y
9.0036977,,
. W 'l
+ 310,e
13 36 13 38,88
9 7715818,9
28,7 14
44 ЗІ 09.81
9.7538923,,
30,5
16 20 39 18,78
9 5476-65,9 55.8
17 16 32 00,48
9.4541973,0
70,9
19 30 43 09,87
9.7082799,4
35,4
20
41 17 12,18
9 8194304,,
23,9
ї ї
2 .
9.0_'71884,2
9.0275200,3
2 2
9.0275200,3
W 2
-3 1 6 ,,
8
60 23 16,23
9.1>392146,8 1 2 , 0 7
70 14 01,19
9.9736263.9
7,5
10 + 13
66 02 0!), 18
9.9608127.6 9,3 9 + 14 54 08 31,09 9.9087374.e
15,2
14 34 34 09,81
9.75 8923,,
30,5
13
Д6 13 38,88 9.77І5818,9
28,7
V
" 1
9.6539497,6
9.653945/,4
9.6539457,4
w 3
+ - i o >2
Умовні рівняння третьої групи
4,77 (2) —6,37 (3) +1.87 (5) —2,4в (6) + 5,92 (9) —3,67 (10) +31,06=0,
2,87 (13) —3,05 (14)+ 5,58 (16) —7,09 (17)+ 3,54 (19) —2,39 (20)—31,61 =0,
-0,75 (7) +1,20 (8) -^-.1,52 (9) +0,93 (10) —1,94 (13) +1,53 (14) + 4,02=0.
Вагова функція
/•'=lg EF=F0-7,5 (7) + 9,3(10) + 7,чП ) + 7,4(12) + 9,3(13) + 30,5(14).
№
1
2
З
4
5
6
7
8:
9
10
11
12
13
14 :
15
16
17
18
19
20
1
с
. л А' ДА' '
В'
Д В'
0
0
0 + 0,870 0
+ 0,293
0
<
0
+ 3,625
+ 0,026
0
+ 0,293
0
0
-6 ,1 4 5
+ 1,624 0 -0 ,5 8 7
0 0
0 + 0,817
0
—0,293
0 0
+ 2,770 + 0,064
0
+ 0,587
0
0
-3,625 -0,026
0
-0 ,2 9 3
-0 ,7 5
-0 ,7 5
0
+ 0,68^
0
— 1,467
+ 1,20 0
0
-2,376 0
+1,467
-1,5 2
0 + 6,145
-1 ,6 2 3 0
+ 0,587
+ 0,93
+ 0,93 -2 ,7 7 0 — 0,064
0
0,587
0
+ 0,74 0
+ 1,532
0
— 1,888
0
+ 0,74
* о
-1 ,5 3 2
0 + 1,045
-1 ,9 4
+ 0,93
0
+ 0,613 + 4,980
—1,039
+ 1,53
+ 3,05
0
-0 ,6 1 ‘3
-3 ,2 9 5 + 0,196
0
0
0
+ 0,306
0 + 0,189
,0
0 0
+ 0,306 + 3,985
—0,232
0 0
0
-0 ,6 1 3
-4 ,9 8 0
+ 1,039
0
0 0 -0 ,3 0 6 0 + 0,654
0 0 0
+ 0,613
+ 3,925 -0 ,1 9 6
0 0 0
-0 ,3 0 6
-3 ,9 8 5
+ 0,232
рівнянь третьої групи 1 вагової ф ункції
д с
А'
ДА'
А"
В" С"
А п
S '
v’"
-0,8694
+ 0,0387
—3,5612
— 0,347
+ 0,187
-0 ,1 14
+ 0,870
+ 0,293
—0,459
+ 0,073
+ 0,777 + 0,890
—0,329
0
-0 ,1 3 7 + 3,651
+ 0,293
—0,329
—0,137
+ 3,478
— 1,991
+ 0,028 0
+ 0,064
—4,521
-0 ,5 8 7
+ 0,788
+ 0,064
— 4,256
+ 1,101
+ 0,311 + 0,187
+ 0,160
+ 0,817 -0 ,2 9 3 + 0,199
+ 0,347
+ 1,070 -1 ,4 3 0
— 0,063
— 0,465 —0,018
+ 2,834
+ 0,587
—0,528
—0,483
+ 2,410
-0 ,5 61
+ 0,329
0
+ 0,137
—3,651
-0 ,2 9 3
+ 0,329
+ 0,137
— 3,478
+ 1,991
+ 0,440 -0 ,5 6 2 + 0,196
‘ + 0,689
— 1,467
-0 ,4 2 2
-0 ,3 6 6
— 1,566
+ 0,847
-0 ,4 0 3 + 0,188
-0 ,2 4 2
—2,376
+ 1,467
+ 0,685
-0 ,0 5 4
-0 ,2 7 8
-0 ,3 1 7
-0 ,0 2 8
0
-0 ,0 6 4 + 4,522
+ 0,587
— 0,788
-0 ,0 6 4
+ 4,257
— 1,102
+ 0,064 + 0,465
+ 0,018 -2 ,8 3 4 -0 ,5 8 7
+ 0,529
+ 0,483
-2 ,4 0 9
+ 0,557
+ 0,472
+ 0,370 — 0,463 + 1,532 -1 ,8 8 8
+ 0,472
-0 ,0 9 3
+ 0,023
-3 ,0 8 6
— 0,369
+ 0,370
-0 ,9 0 1 -1 ,5 3 2 +1,045
-0 ,3 6 9
-0 ,53 1
— 1,387
+ 2,686
+ 0,393
+ 0,465
-0 ,4 8 9
+ 0,613 + 3,941 —0,577
— 0,024
+ 3,953
+ 1,674
-0 ,2 9 0 + 1,525
-0 ,8 76 -0 ,6 1 3
—3,099 + 0,475
+ 0,649
-2 ,5 8 8
— 1,278
— 0,314
-0 ,3 7 0 + 0,514
+ 0,306
+ 0,189 -0 ,3 1 4
+ 0,144
+ 0,325
+ 0,859
—0,263 0
— 0,168
+ 0,306
+ 3,753
-0 ,2 6 3 -0 ,1 6 8
+ 3,628
+ 0,816
— 0,393 —0,465 + 0,489 -0 ,6 1 3
—3,941
+ 0,577
+ 0,024
-3 ,9 5 3
— 1,674
+ 0,211 — 0,370
+ 0,851
—0,306
+ 0,654
+ 0,211
+ 0,481 +1,040
-0 ,4 6 0
+ 0,290
— 1,525
+ 0,876 + 0,613 + 3,099 —0,475
-0 ,6 4 9
+ 2,588
+1,278
+ 0,263
0
+ 0,168
-0 ,3 0 6
-3 ,7 5 3 + 0,263
+ 0,168
-3 ,6 2 8
— 0,816

Умовні рівняння сум 1— 6 виражають умови, щоб суми
зрівноважених значень виміряних кутів при пунктах А, В, С.
Э дорівнювали кутам при цих точках між твердими ,напря
нами на ці пункти.
Умовні рівняння горизонтів 7 і 8 виражають умови, щоб
•.уми врівноважених кутів при центральних точках Е і F до-
пвнювали 360°.
Геометричний зміст фігурних і полюсних рівнянь нам
оке відомий із попереднього викладу.
Розподіл умовних рівнянь на перші дві групи можна
іроводити різними способами. Найкраще робити гак, щоб до,
іершої групи входила найбільша кількість умовних рівнянь,
юдержуючиеь при цьому, звичайно, правил розподілу, відо^
лих із загальної теорії тригрупового врівноваження.
Всі обчислення проводимо в такому порядку:
1. Складаємо умовні рівняння першої групи (табл. 65).
2. Визначаємо первинні поправки за формулою
іе Wj — вільний член умовного рівняння першої групи З ПО'
іядковим номером /, tlj—■ кількість невідомих поправок, що
щадять у це умовне рівняння.
3. Знайдені первинні поправки v виписуємо в основну
;.хєму (габл. 66), виправляємо секунди виміряних кутів і об-
шслюємо вільні члени умовних рівнянь другої групи.
4. Обчислюємо другі поправки за формулою (80,18):
г)"і = pi Wa. -j- qi wp 4- h + mi
- J -
tt wt ,
шкористовуючи таблицю коефіцієнтів p, q, I, m, t (табл. 67).
5. Виправляємо кути другими поправками і за виправ
дними кутами знаходимо коефіцієнти і вільні члени умовних
)івнянь третьої груии (табл. 66 і 69).
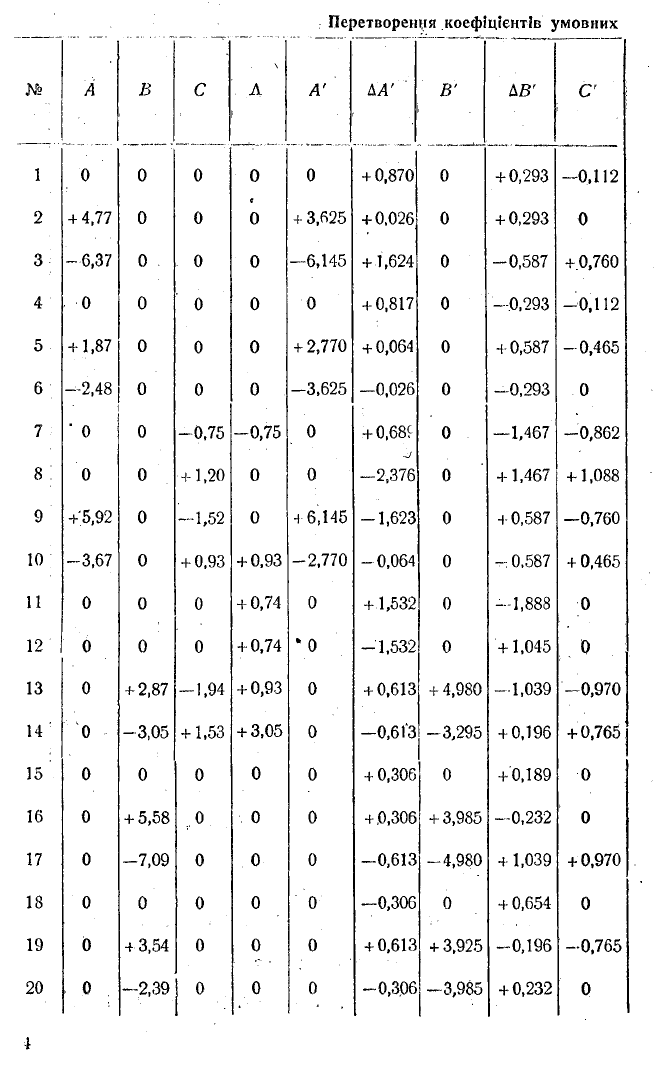
6. Проводимо послідовно двічі перетворення коефіцієнтів
/мовних рівнянь третьої групи за формулами (80,6) і (80,19),
te
дA t'=Pi [А']1
АВ і '= рі [£ ']" + <ь [Д ']"4- - + Ь W \ ll
Д [С'j” + qi [С']‘і 4-■••+*! [С']1}.
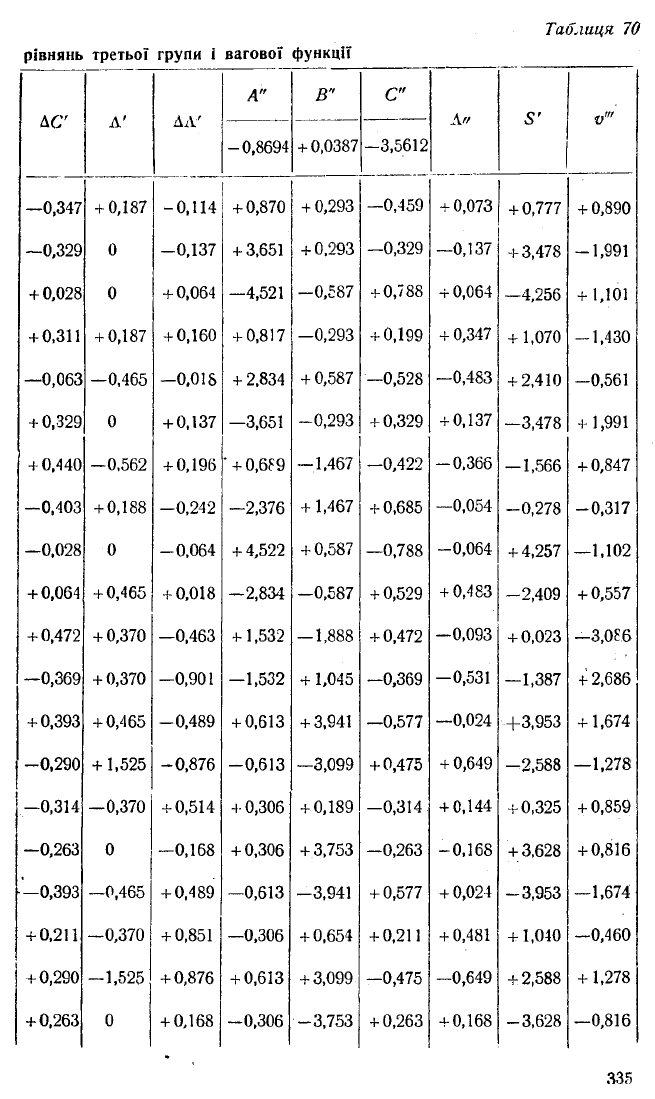
Для зручності обчислень таблицю СЯ неличнн [A')'J,
і [С']|! доцільно розташувати під таблицею 67 коефіцієнті!)
Р, д, А Ш, t.
Всі зазначені в цьому пункті обчислення проводяться в
таблиці 70.
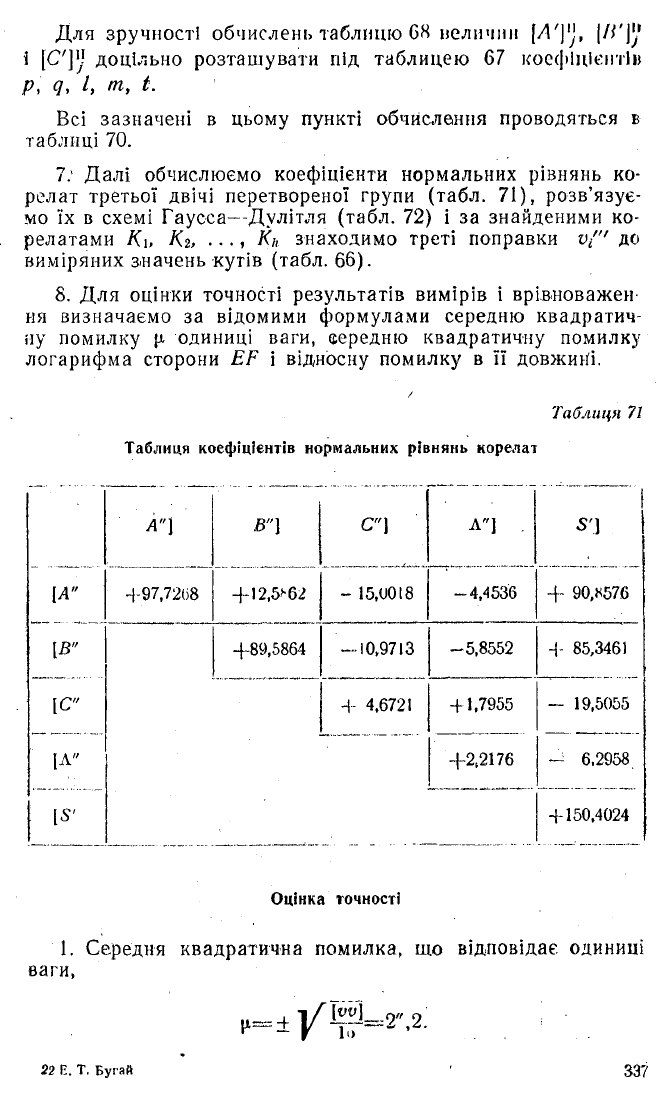
7: Д алі обчислюємо коефіцієнти нормальних рівнянь ко
релат третьої двічі перетвореної групи (табл. 71), розв’язує
мо їх в схемі Гаусса— Д улітля (табл. 72) і за знайденими ко-
релатами Ки К2, • • •, Кь знаходимо треті поправки v{" до
виміряних значень кутів (табл. 66).
8. Д ля оцінки точності результатів вимірів і врівноважен
ня визначаємо за відомими формулами середню квадратич
ну помилку {л одиниці ваги, еередню квадратичну помилку
логарифма сторони EF і відносну помилку в її довжигіі.
Таблиця 71
Таблиця коефіцієнтів нормальних рівнянь корелат
\А"
[В"
\С"
[А"
[5'
А" 1 В" і
С"\
А "] .
1
S’]
+97,7268
+ 12,5^62
- 15,0018 — 4,4536
+ 90,N576
+ 89,5864 — 10,9713
-5 ,8 55 2 + 85,3461
+ 4,6721
+ 1,7955
+ 2,2 176
- 19,5055
- 6,2958
+ 150,4024
Оцінка точності
1. Середня квадратична помилка, що відповідає одиниці
ваги,
тл.
Розв'язування нормальних рівнянь корелат
*
гг
st
З
*2
со
Со
+ 1
S
C O с о
О- г-
со — *-*
О со со
—“о* о'
со
+
СО Г-
f'- СП
LQ СЧ
00 05
О О
05
4- і
CQ
яэ «
ж я
СО X
О О)
с *
tr со
со *о
Ю Tt*
^ О
I +
f I
оо ю со
— со со
C if i T f
с ^-ю
ю ' о* о "
+
СЧ ОО о
СО 00 ю
со сч
о
1 0 -0
СЧ с? о “
+ 1 I
00
со
сч
+
ч*
05
• со
•—< СО ОС •**
СО — Tt* сч
со о со со
t*- 1-«* О *ч*
СО іО со* о "4
иг: і— > СО
+ 1 + 1
lO N t t O O lO
Ю ^х NCO
ОС — о со ю
T f f - 05 Г— 05
LO 00* со“
I + + + I
О О 05 00 00
О 05 05 чг ^
— 05 о о о
СО о .
СО ГГ Tt*
~
с о
if? о" о “
со со
1 н—ь
— ■ г- сч
со ■гГ
't O ,T-v'
со Г- СО 00
1C 1-Г СО О*
00 Г *
+ I + !
СЧ 05 СО о
LO СО — о
ю ю оо со
O0N. сч о
ю о “ ю о "
1 + 1 +
со о со 00 г-н
— СЧ О) сч со
С^- СО СО о СО
05 05 О со
с?-^о? с? с?
Ї+ І + І
о со — ю сч
О Г- СГ ОС f-H
СЧ со to СЧ СО
О^ Г--. СО — Ю
СО Ю со**
+ + I + I
ю сч t-- со
IC N N 0 5 10
О ^ СО О 05
1C 05 Ю О со
сгГ со“ n-“ сч” ^
7 + + + і
ОО Ю Ю 05 СО
ЮО^^'СЧ
05 Tt* СЧ 05
сч — Th t-*- чг
СО г*? ^ —Г
I н—Ь і +
Ю -’УОН
lij -+ СЧ Oi ю
05 ОО -*• СО 05
t - СО Ю со
^ с> о" с? о*
+ 1 1 + 1
со — 05 00 00
г^. СО СО ЧГ сч
О сч г-.
Сч СЧ СО СЧ
СЧ о “ О o ' 1-?
+ 111 +
— 00 сч — сч
сч сч о . о *—•
I-. © СЧ со
СО СО 05 ІО
тг СЧ о " —1 СО
+ 1 1 + 1 1
к .
Tt- — со Ь -
<0 — 1о 00
00 СЧ СО СО
ю со со о
05 —** t— Г-н с Г
СО 00
+ I + I +
^ Ю со Г*- 00
о> о — сч СО ^
Ю со 1“- 00 O i
147,25

2. Середня квадратична помилка логарифма сторони
, Iа . 12.1
/Иіг № = ± у -= - = ± То-г.
3. Відносна помилка довжини сторони EF
1 1

ПОСЕРЕДНІ ВИМІРИ, ЗВ’ЯЗАНІ УМОВАМИ
§ 84. ТЕОРІЯ ВРІВНОВАЖЕННЯ ПОСЕРЕДНІХ ВИМІРІВ,
ЗВ’ЯЗАНИХ УМОВАМИ
В главах V і VI розглядалися питання врівноваження
результатів безпосередніх вимірів відшукуваних величин, ос
гаточні значення яких повинні задовольняти певні матема
гичні умови. Але в геодезичній практиці зустрічаються ви
падки, коли найімовірніші значення невідомих величин дово
диться визначати з сукупності рівнянь помилок і умовних
рівнянь. Така задача зустрічається, наприклад, при врівпо
важенні кутів тріангуляції, якщо рівняння помилок, які ви
микають на станції, доводиться розв’язувати сумісно з умов
ними рівняннями, які виникають в даній тригонометричній
сітці, або при врівноваженні тріангуляції методом врівнова
ження посередніх вимірів, якщо в ній є тверді сторони, ди
рекційні кути та інші елементи, зв’язані з координатами тих
точок, положення яких необхідно знайти- Скорочено подібні
задачі називають врівноваженням посередніх вимірів з умов
ними рівняннями.
Умови задачі такі. Припустимо, що були одержані резуль
гати L\, L2
.........
Ln вимірів п функцій відшукуваних t нев'ідо
михх,, х2, ..., xt, які повинні задовольняти г умовних рів
яянь:
<Рі (*„ х 2, .... xt ) = 0,
ср2 (х „ х 2, .... X t ) = 0,
•
.
............................................ (84,1)
«Рг ( * 1 , * 2
...........
Xt) = 0 .
Необхідно знайти найімовірніші значення невідомих.
Ця задача має значення лише при умові п>^— г. Справді,
через те, що умовні рівняння (84,1) повинні точно задоволь
нятися знайденими значеннями невідомих, то f>r. В против
ному разі при не виникала б і задача на врівнова
ження. При r<7 кількість незалежних невідомих дорпилова
ТИМЄ t — Г, тому ЩО з г умовних рІВ,НЯ'НЬ ми можемо визна
чити г невідомих у функції решти t—г невідомих. Але, з дру

гаго боку, кількість вимірів п, кожному з яких відповідає
рівняння помилок, повинна бути більша від кількості неза
лежних невідомих. Отже, звідси випливає умова:
n>t-r. (84,2)
Для визначення найімовірніших значень величин хи хч.
. . ., X t можемо скласти п рівнянь помилок:
аі (^і) Л’Ь\ (х2) (х‘ h—v\>
а, (.*,) н- Ь2ІХ,і + ...-|-г2 (xt ) + l2=v2,
........................................................................... (84,8)
а п (-^ і) -\~Ьп (Х2) tn (Xt
де (jti), (х2), (X/) — найімовірніші поправки до набли
жених значень невідомих. їх необхідно знайти при наявності
умовних рівнянь (84,1).
Розв’язувати задачу можна такими двома способами.
1. Спосіб попереднього виключення умовних рівнянь. Візь
мемо умовні рівняння (84,1), які можна записати в такому
лінійному виді:
а1(х1)-\-и2(хг) a.t (xt )+w,=0,
Pi (*i) И 2 (■*•>) ! -•••+ Р/ (xt ) + w2=0,
.............................................................................. (84,4)
Pi (*l) + P2(*2)-|--+P< (*t ) + ®V =0,
і визначимо з них значення, наприклад, перших т невідомих
поправок, виразивши їх як функції решти t—г поправок
Припустимо, що ці функції в загальному виді виглядати
муть так:
(ЛГі)=Фі{(Л-,+|), (хг+і), ..., (xt )},
(ЛГ2)=Ф2{(Л:Г+,), (Хг+'г), (xt )},
................................................................ (84,5)
(хг )= ф , {(*г+і), (хг+2), (xt )}.
Підставивши ці значення г поправок у рівняння (84,3),
після відповідних перетворень одержимо систему рівнянь по
милок, В яку входитиме лише t— Г поправок (xr+l ), (Х/-+?), • ,
( Хг )■
Розв’язуючи одержану в такий спосіб систему при умові
[pvv] = minimum, знаходять поправки (хг+і ),(хг+Л ...П ід
ставляючи їх у рівняння (84,5), одержують значення перших
г поправок. І, нарешті, для визначення найімовірніших по
правок Wi, v2, .... vn до результатів безпосередніх вимірів
Li, L2, необхідно підставити знайдені невідомі (Xj )
(j — 1, 2, ..., t) у рівняння помилок (84,3).

Цей спосіб доцільно застосовувати тоді, коли умовні рів
няння (84,1) можна легко (розв’язати відносно вибра.ної гру
пи г поправок.
2. Спосіб корелат. Щоб визначити найімовірніші поправ
ки (xj)jio наближених значень відшукуваних величин, необ
хідно знайти мінімум функції [pvv] , аргументи якої повинні
задовольняти умовні рівняння (84,4). Як відомо, розв’язання
цієї задачі зводиться до визначення мінімуму такої функції:
Ф— Л {<*1 (-КіЬН'і ( * г ) + -+ А (xt Ж і } 2 +
~\~Рг{а2 (^ і)4 ^2 (Л:2') + ---“Ь^2 iXt ) “Ь А }г_Ь
-\~Рп {an (xL)-\-bn (x 2)-\-...-[-tn(xt )+ / л } 2-f- (84,6)
4 -2^ i{ai (-^2)“Ь- - + а^ (x t ) + w i} +
-(—2^2{Рі (* і)+ Р з (-^г)- Ь“-■ •”\~$t (Xt )~b®2}4"
+ 2 kr {р, (л:1)-)-р:1( х г) + " -| -Р ' (xt )-\-wr }= m in im u m ,
де k\, k2, . . ., k r — корелати (неозначені множники Л а г
ранжа) .
Д ля цього знайдемо часткові похідні функції (84,6) і при
рівняємо їх до нуля:
l— 2pyaiv l-\-2p2a2v2-\-...-\r 2pn апг»л +
-\-2kia.1 -\-2k2^l -{-...-\-2kr Pj— О,
Ф' 2= 2 p ibiy l-\-2p2b2v 2-\-...-\-2p„ bn v n - j -
-)-2k^2 —(— 2 &2P2 ~\~---~\~2kr p3= 0 ,
Ф't =2pit1v1+2p2fzVo-{-...~\-2pn tnvn ~|--
-\-2kyat -f-2 k2ftt — J—2kr pt =0,
або, після скорочення на 2,
\pav]-\-alkl-\-$ik2Jir ...-\-plkr =0,
(Xgfej—j— B^ko—j~...-j-Pokr = 0,
...........................
-------------------(84,7)
fptv\-\-a,t k2-{'...-{-pt kr — 0.
Якщо тепер у цих рівняннях замінимо величини vt (і = 1,
2, ..., п) їх значеннями (84,3) і до них приєднаємо умовні
рівняння (84,4), то одержимо тйку систему з f-f-r рівнянь:
\раа] (х^ІраЩ (*2) + ...-{-[pat] (xt )+<x1fc1+ P A + - +
+ рА = о»
