Цейтлин Н.А. Из опыта аналитического статистика

Подождите немного. Документ загружается.

С уважением, автор.

В своём ответе заместитель главного редактора попросил автора дать более

обоснованное описание возражений. Последовал ответ.

Глубокоуважаемый заместитель главного редактора! …

В попытке убедить рецензент я привел ряд аргументов в пользу развиваемых положений. …

С уважением, автор.

ОТВЕТ на замечания рецензента по статье Цейтлина Н. А. «Попарное сравнение…»

1. Необходимость в попарном сравнении СО возникает чаще всего при сравнении

случайных составляющих погрешности приборов, или методов измерения. Попарное сравнение

СО может быть использовано, например, для выявления подгрупп измерительных приборов,

имеющих равные (желательно – наименьшие) случайные составляющие погрешности среди

множества приборов с разными погрешностями.

Поскольку настоящая статья дважды возвращалась на сокращение, то даже запись

вышеприведенных тривиальных соображений приведёт к превышению заданного объема

рукописи. По мнению автора описывать «специфику задачи» вообще не надо. В математической

формулировке гипотез Н

п0

и Н

п1

отражена вся специфика. Всякому статистику известна

постановка задачи о равенстве СО (см., например, [5, с. 106; 6, с. 302 и 398]). В качестве

альтернативы обычно рассматривают разные неравенства. В статьях не принято подробно

описывать общеизвестные методы; достаточно привести ссылки. Такими ссылками в моей работе

являются [3] и [4].

Предвидя повторное возражение рецензента, автор предлагает для рассмотрения следующее

дополнение к статье.

Обычно нулевая гипотеза

2222

012

:...

σσσσ

====

в разных задачах проверки гипотез

относительно ряда СО σ

, σ

, ..., σ

одна и та же [l – 6]. Различаются эти задачи альтернативами.

Так, с помощью критерия Бартлетта [9, с. 144] проверяют гипотезу H

против одной альтернативы

(

)

:ln0

Hσσ

≠

∑

; по критерию Кохрена [9, с. 145] рассматривают другую

альтернативу

{

}

:max1/

σσ

∈

∑

; по критерию Хартли-Дэвид [9, с. 145] – третью

альтернативу

{

}

{

}

:maxmin1

H σσ

∈

Однако на практике часто бывает необходимо выполнить более тонкое - попарное сравнение

СО [3]. Например,

1,11

: , 1,1

iiii

Himσσ

<=−

, или такое [9, с.146] как в методе Дэвид [11]

: , ,1,,

nii

Hijmij

σσ

≠∈<

2. Совместная проверка l нулевых гипотез понимается просто. Записаны l гипотетических

равенств (23) H

: σ

= σ

, 1 ≤ i < j ≤ m; (

ln ,1=

). Если все Н

п0

не отклоняются, значит все СО

равны между собой; если хотя бы одна из Н

п0

отклоняется, то между собой равны не все СО.

Кстати, так же формулируются гипотезы относительно центров СВ [5]. …

В правильности выводов рецензент может убедиться и сам, если сравнит простой расчет в

статье со сложным расчетом по методу Дэвид. Автор не хотел загромождать статью подобным

сравнением. Нo специально для рецензента его приводит.

Пример. Разнообразие свойств продукции, выпускаемой пятью машинами, характеризуется

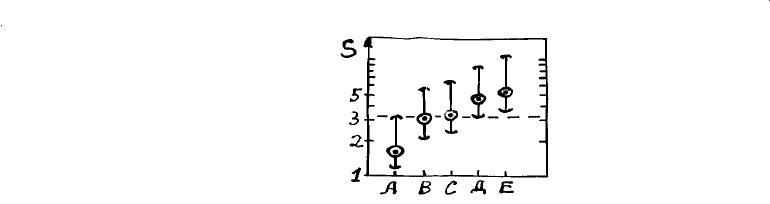
следующими СО [11] с равными числами степеней свободы f = 9 (Таблица).

Таблица

Машина А В С Д Е

СО 1,67 3,07 3,42 4,74 5,3

-------------------------------------------------- по Дэвид

[11]

------------------------------------------------------------------

-------------------------------------------------------------------

группировка

(подчеркнуто)

по МДИ

------------------------------------------------------------------

Необходимо выполнить попарное сравнение СО и разделить машины на множества

равноточных классов.

Решение. Зададим критический уровень значимости α

= 0,05. Число сравниваемых пар

l = 5*4/2 = 10. По номограмме (рис. 2) при α = α

/ l = 0,005 и f = 9 находим доверительную

вероятность 1 - P = 0,963; находим верхние Р/2 - пределы распределения Фишера [1] F

9; ; 0,0185

= 2,2;

;9; 0,0185

= 3,7. По формуле (3) строим 10 границ пяти ДИ (рис. 3).

Рис. 3. Сравнение среднеквадратичных отклонений S, характеризующих разнообразие

свойств продукции пяти машин методом доверительных интервалов: А, В, С, Д, Е – типы машин.

Из рис. 3 видно, что множество машин можно разделить на два пересекающихся класса

(Таблица). Полученные результаты почти совпали с результатами классификации по методу Дэвид

[11]. Отметим, что разные критерии проверки одних и тех же гипотез могут давать сходные, но не

обязательно в точности совпадающие результаты. Подробнее об этом см. в [11, с. 128].

Машины А и Д попали в один класс потому, что вспомогательная горизонтальная прямая

(пунктир на рис. 3) касается верхней границы интервала А и нижней – Д.

Автор Н. А. Цейтлин

Переписка с заместителем главного редактора закончилась вердиктом рецензента.

Повторная рецензия на статью Н. А. Цейтлина «Попарное сравнение…»

Автор не счел целесообразным переработку текста статьи, а только написал подробный

ответ на рецензию. Поэтому основные замечания рецензии остаются в силе, и можно их повторить

с учетом ответа.

1 - 2. По существу, автор предлагает построение совместных доверительных интервалов для

дисперсий на основе критерия Фишера-Бонферрони (24) или графическую иллюстрацию этого

критерия. Однако он не только рассматривает проверку основной гипотезы H

, но и на её основе -

выделение однородных по дисперсиям групп данных.

В ответе автор отчасти признает нечеткость постановки задачи и немного её поясняет,

однако, все же недостаточно четко - в частности, относительно выделения групп данных.

В ответе на п. 1 автор частично дает ответ на замечание 2. В связи с этим особенно

странным кажется грубый ответ на замечание 2 (который даже противоречит сказанному выше

автором).

3. По-видимому, именно переход от случая m = 2 к общему случаю должен содержать

анализ разбиений данных на группы. Эти вопросы применительно к другим методам

обсуждаются, например, в монографиях [11] и Г. Дэвид «Метод парных сравнений», M.:

Статистика, 1978.

4. Ссылки на более поздние работы указать нетрудно. Например, это книга Дэвид, а также

имеющиеся там ссылки.

5. Следует также отметить, что построение совместных доверительных интервалов на

основе неравенства Бонферрони может приводить к слишком широким доверительным

интервалам, практическая ценность которых может быть невелика [11].

Остается сожалеть, что автор не пожелал доработать статью, хотя это было бы не очень

сложно. Однако замечания, высказанные в рецензии и не снятые автором, считаю

принципиальными, поскольку они относятся к постановочной части статьи и, особенно - к

возможности применения предлагаемого метода для решения практических задач.

Таким образом, вывод остается прежним: статью нельзя рекомендовать к опубликованию.

Подпись рецензента отсутствует; копия верна. Зам. главного редактора …

После этого ответа автор съездил в Москву на очередную конференцию по планированию

экспериментов и математической статистике, где, между прочим, познакомился с коллегой

А. И. Орловым, человеком доброжелательным, но принципиальным. Затем многострадальная

статья была вновь направлена для публикации в журнал Заводская лаборатория. Ответ был

получен непосредственно от рецензента.

Дорогой Натан Абрамович! … Посылаю копию своих отзывов на Вашу статью в ЗЛ.

(Дружба - дружбой, а служба – службой!)

С уважением, А. И. Орлов.

Отзыв на статью № 2268: Цейтлин Н. А. «Попарное сравнение…»

Автор считает, что результаты измерений подчиняются нормальному закону и

рассматривает следующие задачи.

1. Пo выборке получить точечную и интервальную оценки среднего квадратического

отклонения (СО).

2. Проверить, что СО для двух выборок совпадают (с. 5-6).

3. Даны несколько выборок. Проверить ряд гипотез о попарном совпадении СО (с. 10).

Классические решения этих задач общеизвестны – см., например, [12]. В задаче № 3 обычно

проверяют равенство всех СО с помощью критериев Бартлетта и Кохрена (табл. 4.3 в [12]).

Фактически автор рассматривает задачу 3 в более узкой постановке - все СО сравниваются

между собой попарно. Это значит, что постановка является классической: проверяется равенство

всех СО между собой.

Видимо, Н. А. Цейтлин не подозревает о существовании статистик Бартлетта и Кохрена,

поскольку для аналитического решения задача 3 использует предложенную в его предыдущей

работе, опубликованной в ведомственном сборнике, статистику Фишера-Бонферрони. Она

сводится к тому, что в критерии Фишера для каждой пары уровень значимости уменьшается во

столько раз, сколько пар сравнивается. Ошибочность этого метода очевидна из того, что

результаты попарных сравнений зависимы между собой.

По указанной причине предложенное автором решение задачи 3 «графическим методом

доверительных интервалов» (ДИ) также принципиально ошибочно.

В задаче 2 автор предлагает для проверки гипотезы использовать ДИ. Если они не имеют

общих точек, то гипотеза отклоняется. При этом доверительная вероятность и уровень значимости

связаны уравнением (10). Автор пытается решать его с помощью различных аппроксимаций для

обратной функции распределения Фишера, но в итоге приходит к аппроксимациям (21) и (22) с

относительной погрешностью 14% и 5% соответственно, что явно неудовлетворительно.

Какие-либо преимущества графического метода по сравнению с классическим не указаны.

Недостатки же ясны - необходимость различных номограмм, графиков, отмеченная выше

недостаточная точность.

Статья написана как методическое пособие, а не как научная публикация. Объем её - 20 стр.,

т. е. вдвое больше принятого в «Заводской лаборатории».

Есть ряд более мелких погрешностей. В замечании на с. 2 автор отмечает, что обычная

оценка СО является смещенной. В грамотных практических расчетах используют множитель,

устраняющий смещение (см. например, [12]). Так что автор напрасно считает, что «в практических

расчетах смещение не учитывается». Ha с. 3 распределение хи - квадрат и распределение Фишера

спутаны. И т. д. Публикация в «Заводской лаборатории» нецелесообразна. Автор может связаться

с рецензентом.

А. И. Орлов.

Дорогой Александр Иванович! …

Ответ на отзыв рецензента на статью №2268 Цейтлин Н. А. «Попарное сравнение…».

Автор выражает признательность рецензенту за проявленное внимание к работе, однако не

согласен с замечаниями и выводом оппонента о нецелесообразности публикации. Во всяком

случае, автор просит дать разъяснение по следующим замечаниям.

1. В работе постепенно развивается подход к попарному сравнению СО Н

по

: σ

= σ

;

1 ≤ i < j ≤ m (формула (23)) против двухсторонних альтернатив

()

: σ

≠ σ

, n =

. Заметим,

что в «классических» постановках (см., например, [1, с. 70]) нулевые гипотезы выглядят

одинаково (например, в книге [1] записана нулевая гипотеза Н

2222

...

σσσσ

====

), но

альтернатива не указана! Этот, вообще говоря, общий недостаток описания задания для проверки

гипотез часто встречается в литературе. Например, гипотеза

(1)

012

σσ

против

112

σσ

≠

проверяется совсем не так, как гипотеза

(2)

012

σσ

против

112

σσ

«Классическую» постановку альтернативы можно сформулировать, например, и так

, 1,

iim

∃∈ :

σσ

≠

(существует такое i из множества

, для которого справедлива

альтернатива

σσ

≠

). Однако удобнее всего альтернативу формулировать непосредственно по

проверочной статистике. Например, по Бартлетту [1, с. 64], как Н

(

)

ln0

σσ

≠

∑

[12], а

по Кохрену [1, с.70]

{

}

:max1/

iii

σσ

∈

∑

Если бы рецензент рассмотрел альтернативы в «классической» постановке, то заметил бы,

что постановка альтернатив

()

в нашей статье отличается от «классической» постановки тем,

что в статье СО

сравниваются попарно. Может даже получиться такой «естественный» в

теории проверки гипотез «парадокс». Например, при

1,3

: σ

= σ

, σ

= σ

, но σ

≠ σ

! Очевидно,

что из всех нулевых гипотез σ

= σ

гипотезы σ

= σ

, σ

= σ

, … σ

m-1

= σ

, совпадают с

«классической» нулевой гипотезой σ

= σ

= … = σ

= σ. Отсюда следует, что замечание рецензента

«автор рассматривает задачу в более узкой постановке» – неверно! Как раз – наоборот: автор

рассматривает задачу в более широкой постановке, в которой «классическая» постановка является

лишь частным случаем.

Далее рецензент считает, что использование статистики Фишера - Бонферрони ошибочно

потому, что результаты попарных сравнений зависимы между собой. По-видимому, рецензент не

знаком с работой Миллера [14, с. 8], который показал, что такая зависимость в действительности

не является столь существенной, если m не слишком велико (m ≤ 5), а уровень значимости α мал

(α < 0,01). Такого же мнения придерживался Фишер [15], который предложил t-статистику (я

пишу «Стьюдента-Бонферрони» [3]) для проверки совершенно аналогичной группы гипотез

относительно математических ожиданий

: ; : ,

nijnij

νννν

=≠

1, 1,,

ijnnl

≤<<=

(

)

llmm==−, где

- число пар альтернатив. Подробнее см. в [3, 13 - 15].

Почему статистика Фишера – Бонферрони до сих пор широко не использовалась для

проверки гипотез

()

? По-видимому, пользователей удовлетворяли статистики Бартлета и

Кохрена. Правда, что делать при отклонении нулевых гипотез, эти статистики не говорят. По

существу статистика Фишера-Бонферрони аналогична статистике Стьюдента-Бонферрони и

является ненамного более «ошибочной». По этой причине предложенный в работе метод ДИ не

является «принципиально ошибочным», как утверждает рецензент.

Не ясно, чем руководствуется рецензент, когда утверждает, что погрешности 14% и 5% «не

удовлетворительные». Следует напомнить рецензенту, что исходный «критический» уровень

значимости α

выбирается исследователем из множества значений 0,01; 0,05; 0,1 (а иногда и 0,001,

или 0,2), различающихся на 1000% и более! Так что ошибка даже 50% для аппроксимации была

бы не столь велика! Во всяком случае, ошибка 14% с лихвой перекрывает все погрешности

практики и поэтому более, чем удовлетворительна! Отмечу также, что рецензент занимает

ортодоксальную позицию математиков-статистиков (в этом вопросе), подвергнутую резкой

критике И. Грековой [16].

Рецензент пишет: «автор пытается решать его (уравнение (10) – Н. Ц.) с помощью

различных аппроксимаций, но в итоге приходит к аппроксимациям (21) и (22)…». Слова «но в

итоге» показывают, что рецензент неточно понял суть изложенного. Поясняю.

Дело в том, что в работе записана точная формула (10), дающая зависимость 1 – Р от α, f

в неявном виде. Решение формулы (10) - дело техники. Только некоторые примеры такого

решения и рекомендации даны в работе. Так вот, слова «в итоге» следует отнести к формуле (10),

ибо она и есть итог, а остальные формулы лишь выражают мнение автора о практическом

использовании этой формулы.

На с. 2 рецензент повторяет неверное утверждение, что «автор предлагает графический

метод для решения классических задач». Приходится повторить, что поставленная задача - не

«классическая», а общая.

Можно поспорить с рецензентом, что стиль изложения «как методическое пособие» хуже

стиля «как научная публикация». Мы пытались четко ставить «задачи», «примеры», «замечания».

Не существует каких-либо указаний, скажем, редакции «Заводской лаборатории» о том, какой

стиль изложения следует использовать.

Нельзя согласиться с рецензентом, когда он пишет, что 20 стр. - вдвое больше принятого в

«Заводской лаборатории». Возьмём первую попавшуюся «свежую» статью в журнале № 3, 1987,

стр. 41- 48. Это - почти 7 стр. текста, что в переводе на машинописный текст - около 22-х страниц.

Далее рецензент тактично упрекает автора в неграмотности «в грамотных практических

расчетах используют множитель, устраняющий смещение…»

Нам представляется, что использование авторитетов в данной дискуссии неубедительно.

Цитируемым авторам книги [12] мы можем противопоставить не менее «грамотных» авторов [5 с.

73], которые названный множитель не используют.

Рецензент, по-видимому, не обратил внимания на приведенные в статье аргументы.

Попытаемся дать разъяснение.

Величина смещения

(

)

dSf

= не превышает СО

()

0,5

SSN= ошибки величины S

Это значит, что как несмещённая

YYs

SSd

, так и смещенная

оценки СО являются

незначимо различающимися оценками генерального СО

Наш спор можно сформулировать в терминах теории проверки гипотез. Если смещенная

→, а несмещённая

нн

→, то позиции автора и рецензента записываются как нулевая

гипотеза

σσ

против альтернативы

σσ

. Рецензент «заинтересован» в

альтернативной гипотезе

, автор - в нулевой

. Очевидно, что оснований для отклонения

гипотезы

нет, так как

! Покажем это на упомянутом [5, с. 73] примере.

Дано: выборка {27, 22, 24, 26}

⊂

ImY,

(

)

~,YN

νσ

. Находим

()

2,217

S=, смещение

0,1848

, откуда

()

2,402

S=; СО ошибки

равно

0,7840

. Величина смещения

более, чем в 4 раза (в 4,243) меньше СО

! Неужели эти факты не убеждают рецензента в том,

что наличие смещения

СО является интересным только для теории, но не для практики?

Отсюда видно, что грамотные практики не используют множитель, устраняющий смещение не

потому что не знают этого (см. [17, с. 74]), а потому что это смещение не значимо!

Неверно замечание рецензента «распределение хи-квадрат и Фишера спутаны». Мы

используем распределение Фишера

,ff

∞

= вместо распределения хи-квадрат

потому,

что это позволяет применять только одно общее распределение (Фишера) для решения многих

задач (а распределения хи-квадрат, а также Стьюдента являются частными случаями

распределения Фишера). В статье написано (согласно Шеффе [8]), что

12,

- это «верхний α -

предел», а

- это статистика.

Теперь о том, чего не заметил рецензент.

В приложениях существует очень сложная

проблема практического определения уровня значимости

по значениям

и F

распределения Фишера. Известные таблицы (даже в [12]) очень неудобны, громоздки и неполны.

А приведенные в работе номограммы просто решают проблему!

С уважением, Н. А. Цейтлин.

Дорогой Натан Абрамович! На Ваше письмо с датой 23.4.87 я хотел ответить подробно, но

для этого необходимо время, которого нет. Поскольку затягивать ответ уже было бы обидно для

Вас, отвечаю кратко.

В «Заводской лаборатории» довольно обычным является рассмотрение ответа-возражения

автора на замечания рецензента. Иногда итоговое решение пересматривается.

Меня же Ваши возражения не убедили. Правда, теперь я знаю, что Вы знакомы с

критериями Бартлетта и Кохрена. Тогда следует объяснить, чем конкретно Ваша постановка

отличается от их постановки - не мне объяснить, а в статье.

Разбирались ли Вы с имеющимися в дисперсионном анализе методами выделения значимо

различающихся параметров (дисперсий у Вас)? См. статьи Е. В. Марковой и др. в «Заводской

лаборатории».

Пожалуй, Вы правы, что для инженера изложение типа методики более предпочтительно,

чем даваемое сейчас в ЗЛ. Но тогда пришлось бы увеличить объем журнала раз в 10. Поскольку

это невозможно, авторы должны приспосабливаться к реальности.

Фишер, конечно, голова, но со времени его работ много воды утекло. Поэтому цепляться за

него нечего. …

В Вашем письме встречаются разнообразные ссылки, которых не было в

прорецензированной статье, а потому в этой статье Вы выглядели слабее, чем на самом деле.

Так зачем же Ваша сложная процедура нужна, зачем возиться с Вашей формулой (10),

решать уравнения, когда есть статистики Бартлетта и Кохрена? Если Вы пишете, что Ваша

постановка - более общая, то где конкретно нужна Ваша общность? И не покрывается ли эта

общность известными результатами современного дисперсионного анализа? На такие вопросы в

статье надо отвечать аргументировано.

Если Вы пишете статью для ЗЛ, то целесообразно ознакомиться с правилами для авторов.

Статья в ЗЛ № 3 за 1987 г., с. 41-48 – обобщающая; на такую, или обзорную статью допускается до

20 машинописных страниц, а на остальные - до 10 стр.

Книга Л. Закса [17] - пример безграмотного сочинения.

По поводу распределения Фишера. Г. В. Мартыновым (МГУ) разработана программа,

позволяющая считать всё что надо - см. «Статистические методы оценивания и проверки гипотез.

Межвузовский сборник научных трудов» – Пермь, Пермский гос. университет, 1986.

Я думаю, что Вам было бы неплохо написать статью типа «Опыт использования

прикладной статистики в содовой промышленности» с указанием конкретных заводов,

технологических процессов, экономического или технического эффекта. Подборки такого типа

статей я готовлю для журналов «Стандарты и качество» и «Надежность и контроль качества». …

Всего Вам доброго! Ваш А. Орлов.

Дорогой Александр Иванович!

Спасибо за письмо и внимание которые Вы уделяете моей работе. Постараюсь ответить по

пунктам.

1. Мне кажется, что разъяснять читателю отличие моей постановки проверки гипотез от

постановки, приводящей к критериям Бартлетта и Кохрена не надо: во-первых, это очевидно, во-

вторых, занимает лишнее место, а статья и так большая.

2. Е. Маркову в ЗЛ я читал, но посмотрю еще.

3. Мне нравится, как Вы эмоционально пишите о Фишере и, понимая, как надо читать

между строк, постараюсь это сделать. «Не цепляться за Фишера» - это значит «обойти вниманием

его распределение

FSS

= и не тратить усилий на параметрические критерии»?

Ваше письмо порождает больше вопросов, чем дает ответов. … У нас есть еще предмет

разговора – Ваши «рекомендации». Сначала я их читал почти без пометок – «терпел» Ваши крайне

«правые» высказывания, а потом «не вытерпел» и стал чёркать возражениями.

5. «Где нужна общность?» … Видите, сколько я еще должен добавить к статье, чтобы все

разъяснить! А ведь в ней уже 20 с.!

Дисперсионный анализ, даже самый современный – лишь частный случай регрессионного

анализа. Во всех книгах регрессию определяют только как функцию

(

)

ν=, но это – узкое

определение. Например, если рассматривается регрессия случайной величины Y по х, а Y имеет

распределение Вейбулла, то где там функция

(

)

ν=

7. Что значит «общность покрывается известными результатами»? Не «покрывается»: я

решаю задачу иначе (методом доверительных интервалов) и удобней для прикладника: результаты

становятся наглядными и обозримыми. …

8. За что Вы обижаете Л. Закса? Я против его книги [17] ставлю 20 монографий, которые

«зря» читал и которые слабее!

9. Да, некоторый «опыт» у меня есть. У меня уже около девяти почти готовых рукописей

«мини-монографий» по 40-50 стр. каждая на самые разные темы лежат в «долгом ящике». …

Всего наилучшего, Н. А. Цейтлин. 15.06.87.

Дорогой Натан Абрамович!

Отвечаю на Ваше письмо от 15.06.87. Ваша работа рассматривалась на секции редколлегии

18.06.87. Докладывал не я, другой член редколлегии, но он согласился с моим заключением,

добавив: «работа, кроме прочего, неверная».

Считаю полезным высказать несколько соображений о Вашей статистической деятельности.

Насколько могу судить, Вы - самоучка, никогда систематически не обучались теории

вероятностей и математической статистике. Вы с пользой применяете статистику в прикладных

задачах - и в этой Вашей включённости в дела промышленности Ваш большой плюс. Но с

теоретическими основами Вы знакомы слабо. Поэтому Вы не можете в горе книг выделить

основополагающие и вторичные. Другими словами, у Вас «нет школы».

Какие книги считать основополагающими? Сам я учился по «Математическим методам

статистики» Г. Крамера. Сейчас имеется университетский учебник A. А. Боровкова

«Математическая статистика», учебник для втузов Г. И. Ивченко, Ю. И. Медведева

«Математическая статистика». Из справочных пособий необходимо знакомство с книгой [12].

Без знания основ невозможен критический анализ «поваренных книг» типа Закса [17]. Равно

как и бесполезны попытки получения самостоятельных результатов в математической или

прикладной статистике.

Теперь - по тексту Вашего письма.

1. Прочитав Вашу статью, я решил, что Вы попросту не знаете критериев Бартлетта и

Кохрена. Всегда полезно четко указать место своей работы среди других.

2. P. Фишер работал давно и не всегда строго. Надо быть на уровне современности.

Е. С. Вентцель полезна своей популяризаторской и литературной деятельностью, но в

методологическом плане забывает про развитие.

3. Рассмотрим пример. Сейчас Ваша деятельность в содовой промышленности явно полезна.

Пройдет лет 20. Вы с теорией не познакомитесь, но станете большим начальником (главным

статистиком отрасли), выпустите 50 ОСТов по прикладной статистике. Придет молодой

специалист по теории вероятностей и математической статистике и найдет массу ошибок в Ваших

ОСТах. Он будет бороться за искоренение ошибок, а Вы будете его травить. Так из

прогрессивного явления Вы станете тормозом на пути развития общества. Именно такова

ситуация у меня с неким Б…

4. То, что одни и те же алгоритмы решают и задачи регрессионного анализа, и задачи

дисперсионного анализа, давно известно. См., например: Маркова E. В., Денисов В. И., Полетаева

И. А., Пономарев В. В. Дисперсионный анализ и синтез планов на ЭВМ. - M.: Наука, 1982. - 195 с.

5. Примеры ошибок в книге Закса [17].

На с. 270 утверждается «Критерий Уилкоксона, Манна и Уитни проверяет нуль-гипотезу:

две независимые выборки принадлежат одной и той же генеральной совокупности, их функции

распределения вероятностей равны: F

(х) = F

(х)». Это неверно. На самом деле с помощью

указанного критерия можно проверить только гипотезу

(

)

(

)

FxdFx=

∫

. Если функции

распределения совпадают, то и эта гипотеза верна. Обратное неверно.

На с. 279 сказано: «U - критерий - это самый строгий непараметрический критерий. Так как

статистика U - очень сложная функция от среднего значения, эксцесса и асимметрии..., то нужно

подчеркнуть, что с увеличением различия между генеральными совокупностями надежность

границ значимости будет уменьшаться».

Трудно в один абзац вместить столько чуши. U - критерий не является состоятельным (в

смысле математической статистики), и его никак нельзя считать «самым строгим». Состоятельные

критерии - Смирнова и омега-квадрат. (См. «Вестник АМН», 1987, № 2, моя статья). Статистика U

не является функцией от среднего и т. д. Последняя процитированная фраза вообще загадочна, не

могу придать ей строгий смысл.

Поскольку подобных ляпов у Закса много, то и отношение у меня к этой книге

соответствующее. Практически нет ляпов в «Таблицах» Большева и Смирнова.

6. Мне представляется, было бы полезно, если бы Вы постарались изучить учебник

Боровкова т. е. выйти на современный уровень. А хоть Левша и подковал блоху кустарными

методами, но это явно не перспективно.

7. Демокрит: «Иные многознайки не имеют ума». Вывод: читать надо хорошие книги.

Простите, если я что - то сказал слишком резко. Я не хотел Вас обидеть, поскольку хорошо к

Вам отношусь (иначе не стал бы писать письма). Но моя оценки ситуации, надеюсь, будет Вам

полезна. Хорошего отдыха и хорошей работы! Ваш А. И. Орлов

02.08.87. Дорогой Александр Иванович!

… Другой член редколлегии добавил: «работа, кроме прочего, неверная». Читал ли он мою

статью, или только конец Вашей рецензии и что именно в моей работе «не верно», я так и не

понял. Слова «другого члена редколлегии» мне напоминают речь Остапа Бендера на смерть

Паниковского: «- Порок сердца, - сказал Остап, чтобы что-нибудь сказать». …

«У Вас нет школы» - это Вы попали в точку. … Половину Крамера (еще «старого») я одолел

в 1977 г. Рекомендованные Вами книги лежат среди других, ждут очереди. Дрейпера и Смита, т. 2

я прочитал в первую очередь! Это книга - на каждый день! …

Я не во всем согласен, когда Вы прогнозируете мою «травлю» гипотетического молодого

специалиста. «50 ОСТов по прикладной статистике» я не выпустил, а только один, но зато

большой. «Молодой статистик» у нас уже есть (и не один) – из моих бывших студентов! И мы

хорошо сотрудничаем, помогаем друг другу и даже дружим.

Ошибки в книге Л. Закса [17] я тоже нашёл: процедуры на с. 270 описаны некорректно, а

правильно описаны у Ивченко и Медведева на с. 129; форма записи верхних α - пределов не

правильная (надо, например, писать

να

, а у него просто -

, и поэтому его трудно отличить от

двустороннего

να

); формула (1.14.3) на с. 152 неверна и т. д. Ряд ошибок в своем экземпляре я

исправил. Но ведь и на солнце есть пятна! Я же видел оригинал этой книги на немецком языке:

там ошибок меньше! Считаю, что книга Л. Закса все же полезная. Просто надо при повторном её

издании попросить редакторов учесть Ваши (и других читателей) замечания.

А в институте началась перестройка: начальников уже «сверху» не назначают, а выбирают

«снизу»! Всех благ, Ваш Н.А.

…

28 июня 2002 г. Дорогой Александр Иванович!

После «небольшого» пятнадцатилетнего перерыва я вновь взялся за ум и математическую

статистику и нашёл работу в НИИ М. Планка (в г. Гёттингене, ФРГ). Страшно обрадовался, когда

обнаружил в запутанной международной паутине Ваш адрес! Теперь у меня появилась надежда,

что Вы, наконец, ответите на моё предыдущее письмо от 02.08.1987 года. Кроме того, у меня

появились две актуальные проблемы, которыми я хочу с Вами поделиться! Дело в том, что я

заканчиваю монографию «Из опыта аналитического статистика» и собираюсь разместить её

сперва в Интернете, обсудить со специалистами, затем опубликовать. В одном разделе я

собираюсь цитировать нашу с Вами незаконченную переписку.

Проблема № 1 – этическая. Я прошу Вашего разрешения на публикацию фрагментов нашей

переписки в прилагаемой редакции (копию Вашего рукописного оригинала переписки я храню как

зеницу своего ока).

Проблема № 2. Я хочу попросить Вас ответить на моё предыдущее письмо от 02.08.1987 и

заодно уж поделиться-таки своим мнением о цитируемом разделе «Попарное сравнение …».

Безусловно, был бы счастлив возобновить с Вами переписку. Кстати, в моём бывшем НИИ -

НИОХИМе, которому я отдал четверть века своей биографии, перестройка, наконец, завершилась

«экономным» сокращением штатов в 20 раз. А чем у Вас завершилась перестройка?

Всех благ Вам, Ваш Натан Абрамович.

Дорогой Натан Абрамович!

Рад получить от Вас письмо. Еще больше рад, что Вы с энтузиазмом занимаетесь

проблемами прикладной математической статистики. Сразу вспомнились 1980-е годы, которые

сейчас воспринимаются мной как счастливые, несмотря на все тогдашние проблемы. Конечно,

тогда был эмоциональный подъем, надежды. А сейчас - спуск. И по возрасту, и по положению

страны. Приношу запоздалые извинения, если не ответил на Ваше письмо от 02.08.1987 г. Однако

возможно, что почта потеряла - либо Ваше письмо, либо мой ответ. Тогда я работал во

ВНИИСтандартизации. Сейчас он сократился не менее чем в 5 раз и стал ВНИИСертификации.

Как раз в 1987 г. начался самый бурный период в моей жизни. Сначала - борьба за отмену

ошибочных стандартов по статистическим методам, потом быстрая смена видов деятельности (в

1989 г. создал Всесоюзный центр статистических методов и информатики, убитый в 1992 г.

гайдаровской «либерализацией», в 1990 г. организовал Всесоюзную статистическую ассоциацию,

погибшую вместе с СССР), в результате - с 1993 г. профессор-экономист (сейчас на кафедре

«Экономика и организация производства» в МГТУ им. Н. Э. Баумана). Но в «Заводской

лаборатории» я по-прежнему действую. Информация о деятельности последних лет имеется на

сайтах www.antorlov.chat.ru, www.antorlov.nm.ru, www.newtech.ru/~orlov, www.antorlov.euro.ru, а

также примерно в сотне выпусков подписки «Эконометрика» (информация о подписке и архиве -

на перечисленных сайтах). Теперь - о Ваших вопросах.

Пожалуйста, помещайте в своей книге фрагменты нашей с Вами переписки. Я всегда

был и остаюсь сторонником открытости информации (гласности).

В присланных Вами текстах надо разбираться. Тем более, что шла напряженная дискуссия,

как между нами, так и у Вас с редакцией журнала. А сейчас - последние дни сессии, и надо все

закончить в трех университетах, в которых я преподаю. Поэтому по существу я смогу ответить

лишь несколько позже.

Одно замечание о термине «аналитическая статистика». Ю. В. Линник (и я вслед за ним

в статьях в «Вестнике статистики») понимал под ней дисциплину, посвященную внутри-

математическому изучению математических объектов, используемых в математической

статистике. В противоположность прикладной математической статистике, черпающей

постановки из потребностей практики. Совсем не тот смысл термина, что у Вас. Для Линника

«анализ» - это термин в ряду «математический анализ», «функциональный анализ» и др.

Всего Вам доброго! Ваш Александр Иванович 02.07.2002.

Дорогой Александр Иванович!

Скажу честно, приятно было получить от Вас столь быстрый ответ. К ответу на ответ мне

надо подготовиться, в частности, ознакомиться с Вашими сайтами и, если Вы позволите,

высказать по их содержанию своё мнение.

Спасибо за замечание. Я пишу «аналитический статистик» (АС). Слова - почти

одинаковые, но первые (по Ю. В. Линнику) относятся к названию математической дисциплины, а

я пишу о профессии. Можно, наверно, говорить о моей профессии и так: «прикладной статистик».

Но круг задач АСа шире: он не просто «черпает постановки из потребностей практики», он

занимается и формализацией задачи экспериментального исследования, и оптимальным

планированием эксперимента, и статистической обработкой результатов наблюдений (иногда - с

привлечением «чистых» математиков и программистов), и интерпретацией результатов расчета в

терминах исходной предметной области, и участвует в составлении научного отчета о

проведенной работе…

Поскольку главное – это уметь отличить важное от срочного, я срочно свидетельствую

оживление пульса нашей переписки.

С почтением, Ваш Натан Абрамович.

1.2.4. Метрология. Исследование погрешности считывания оператором

показаний стрелочного измерительного прибора

Статистика есть наука о том, как, не умея мыслить и понимать,

заставить делать это цифры. (В. О. Ключевский)

В настоящем разделе описаны процедуры метода доверительных интервалов,

используемые при сравнении, как среднеквадратичных отклонений, так и средних значений

нормально распределённых случайных величин.

Существенным слагаемым суммарной погрешности прямого измерения является

субъективная погрешность оператора [1]. Чаще всего такая погрешность обусловлена

считыванием показания со шкалы стрелочного измерительного прибора, реже – при чтении

графиков и номограмм [2]. Основные затруднения у человека возникают при определении на глаз

доли расстояния, отсекаемого стрелкой прибора, остановившейся между двумя делениями шкалы.

С задачей деления расстояния на глаз при считывании связана и обратная задача - установление

стрелки, которая должна разделить расстояние между двумя штрихами в заданном соотношении.

Подобные задачи решают практически все водители транспортных средств, лаборанты, рабочие,

инженеры, торговые работники и многие другие.

Обозначим: X - действительное значение доли, показанное стрелкой, Х

∈

[0; 1];

показание оператора;

∆

= X -

- погрешность показания оператора.

В литературе приведены лишь качественные оценки погрешности

∆

. В результате

обобщения результатов считывания показаний штангенциркуля установлено [1, с. 102], что

погрешность считывания опытным механиком характеризуется малым разбросом, но

существенной систематической составляющей, что объясняется неверными навыками, а у

молодых инженера и слесаря - большим разбросом и несущественной систематической

составляющей, что обусловлено отсутствием опыта. Других сколько-нибудь обстоятельных

исследований этого вопроса в литературе не обнаружено.

Целями одноимённого исследования (Цейтлин Н. А. - В. кн.: Метрологическое обеспечение

измерений параметров состава и свойств веществ и материалов на предприятиях и в организациях

химической промышленности. Труды. Т. 67 / ХНПО "Карбонат". - Харьков, 1988 - с. 89 - 103)

являлись: развитие наглядного статистического метода сравнения систематических и случайных

составляющих погрешностей и описание закона распределения исследуемой погрешности

∆

зависимости от различных факторов. Основными из них являются: факторы, характеризующие

личность оператора (возраст, пол, опыт, профессия, заинтересованность в получении большого

или малого значения измеряемой величины, дефект зрения, самочувствие); факторы,

характеризующие влияние обстановки (интенсивность и вид освещения шкалы; расстояние между

глазами оператора и шкалой, шум, мигание света, вибрация прибора, стрелки, пола помещения,

температура воздуха в помещении, ветер, дождь, положение стрелки между глазом оператора и

шкалой, между штрихами, дефекты углов поворота луча зрения оператора по отношению к

плоскости шкалы, стрелки, штрихов, углы между стрелкой и штрихами, продолжительность

фиксации взгляда на шкалу); влияние конструктивных и геометрических особенностей стрелки и

шкалы (толщина стрелки и штрихов, расстояние между штрихами, радиус кривизны шкалы;

«стрелкой» может служить мениск прозрачной или окрашенной жидкости в термометре,

барометре, бюретке; шкала может быть нанесена на линейки, прозрачные трубки различных длин

и диаметров); длина и цена деления шкалы (обычно цены деления шкалы кратны числам 1; 2; 2,5

и 5).

В настоящем исследовании варьировались лишь такие факторы: «профессия оператора»,

∈

{1, 2, 3} (где числами обозначены: 1 - математик (студент, неопытный оператор); 2 - технолог

(химических производств); 3 – химик-аналитик (специалист по химическому анализу веществ);

операторы q

∈

{2; 3} - опытные); длина деления шкалы, d, мм, и действительное значение X доли,

показанное стрелкой. Остальные факторы фиксировались на благоприятных уровнях.

Исследования выполнены в два этапа. В первом этапе исследований принимали участие 24

очаровательные студентки (в возрасте от 20 до 22 лет) механико-математического факультета

ХГУ (на занятиях спецкурса по прикладным методам математической статистики).