Чейз, Ричард, Б., Эквилайн, Николас, Дж., Якобе, Роберт, Ф. Производственный и операционный менеджмент

Подождите немного. Документ загружается.

Дополнение к главе 7. Линейное программирование

251

Оценка

степени

согласованности

Трое ученых использовали метод линейного программирования

для

оценки слаженности игры игроков

бейсбольной лиги. Модель основывалась

на

вычислении весовых коэффициентов

применялась

для

полу-

чения

объективных показателей слаженности

на

основе субъективных оценок согласованности действий

иг-

роков.

Сравнение результатов анализа

классификационными требованиями позволило подбирать игроков

команду. Такое применение линейного программирования

равной степени подходит

и для

оценки

со-

гласованности работы служащих менеджерами различных предприятий.

Источник.

Christopher

Zappe,

William

Webster

and

Ira

Horowitz,

"Using

Linear

Programming

Determine

Post-Facto

Consistency

Performance

Evaluations

Major

League

Baseball

Players",

Interfaces,

November-December

1993,

107-113.

Оценка

лесных

ресурсов

Когда правительство Новой Зеландии приступило

приватизации государственных лесных угодий,

для определения правильной продажной цены потребовалось оценить ожидаемые потоки денежных

средств

от их

эксплуатации.

помощью линейного программирования была разработана модель лесных

угодий, позволившая определить восстанавливаемые участки лесозаготовок

распределение стволов

в 14

зонах

горизонтом планирования

на 40 и 70 лет.

Рассчитанные показатели ожидаемых денежных пото-

ков

от

этих операций учитывались

при

назначении стартовых

цен и

налогообложении участков леса.

Кроме того, потенциальные покупатели смогли воспользоваться результатами моделирования

для

разра-

ботки своей стратегии торгов.

Источник.

Bruce

Manley

and

John

Threadgill,

"LP

Used

for

valuation

and

Planning

of New

Zealand

Plantation

For-

ests",

Interfaces,

November-December

1991, p.

66-79.

А теперь приготовьтесь!

этом дополнении

главе

мы обсудим основы одного

из

самых мощных инструмен-

тов, применяемых

сфере управления бизнесом,

— ли-

нейного программирования.

Понятие

линейного программирования

(Linear Program-

ming

— LP)

включает несколько взаимосвязанных мате-

матических методов, которые используются

для

опти-

мального распределения ограниченных ресурсов предпри-

ятия

между

его

конкурирующими потребностями. Наибо-

лее широко линейное программирование используется

методах, объединенных единым названием "матема-

тические методы оптимизации",

и, как вы

убедились,

прочтя врезку "Типичное применение методов линейного

программирования

операционном менеджменте",

ока-

зывается незаменимым

при

решении очень многих задач

этой области.

данном дополнении

мы

сосредото-

чимся

на

обсуждении симплексного метода,

помощью

которого решаются любые задачи линейного программи-

рования,

также

на

описании графического

транспорт-

ного методов, которые очень эффективны

при

решении

конкретных специфических задач.

Мы не

только проде-

монстрируем, каким образом методы линейного програм-

мирования

приводят аналитика

оптимальному решению

поставленной задачи,

но и

обсудим понятие "теневых

оценок"

другую

"бесплатную информацию", которую

получает специалист, применяя симплексный метод.

Для решения задачи методом линейного программиро-

вания

необходимо, чтобы описанная

в ней

ситуация отве-

чала пяти основным условиям. Во-первых,

она

должна

быть связана

ограниченными

ресурсами

(т.е. ограниченное

количество рабочих, оборудования, финансов

материа-

лов

т.п.),

противном

случае

этой задачи просто

бы не

существовало. Во-вторых, необходимо сформулировать

точную

цель

(максимизация прибыли

или

минимизация

затрат).

В-третьих,

задача должна характеризоваться

ли-

нейностью

(например, если

на

изготовление детали

требу-

ется

три

часа,

то на

изготовление

двух

будет

затрачено

шесть часов,

на

выпуск

трех

—

девять

т.д.).

В-

четвертых, задача должна характеризоваться

однородно-

стью

(изделия, изготовленные

на

станке, идентичны;

все

часы,

течение которых рабочий выполняет

ту или

иную

операцию, используются

им с

одинаковой продуктивно-

стью

т.д.). Пятое условие заключается

делимости:

ме-

тод линейного программирования строится

на

допуще-

нии,

что

результаты

ресурсы можно разделять

на

доли.

Если такое деление невозможно (например, полет поло-

вины

самолета

или

наем

на

работу одной четвертой

слу-

жащего), аналитику лучше воспользоваться специальной

модификацией линейного программирования

—

дискрет-

ным

(или

целочисленным)

программированием.

Методы

линейного

программирования

могут

применять-

ся,

если поставлена только одна цель: максимизировать

(например,

прибыль)

или

минимизировать (например,

издержки). Когда целей несколько, используется

целевое

программирование.

Если

же

задача эффективнее всего

ре-

шается поэтапно

или по

временным интервалам, анали-

тику

следует

воспользоваться методом

динамического

про-

граммирования.

В еще

более сложных задачах при решении

могут

потребоваться

другие

варианты данного метода,

на-

пример

нелинейное,

или

квадратическое

програлширование.

252

Часть

III.

Проектирование производственных мощностей и трудового процесса

Модель

линейного

программирования

Формально выражаясь, задача линейного программи-

рования

связана с оптимизацией процесса, в

ходе

кото-

рого отбираются неотрицательные искомые переменные

Х„ Х

, ..., Х

, используемые затем для максимизации (или

минимизации)

целевой функции в следующей форме.

Максимизировать (минимизировать) целевую функцию

при

условии ограничений на количество ресурсов, выра-

женных в таком виде:

где

С„,

и В

— заданные постоянные величины.

В зависимости от типа задачи ограничения

могут

ука-

зываться также с использованием знака равенства (=) или

знака

"больше или равно" (£).

Графическое линейное

программирование

Несмотря на то, что графическое линейное программи-

рование (Graphical Linear Programming) применяется толь-

ко

для решения задач с двумя искомыми переменными

(или

случае

с трехмерными графиками — тремя), этот

метод позволяет быстро понять основную

суть

линейного

программирования и иллюстрирует, что происходит при

использовании симплексного метода, описанного дальше

этой главе.

Порядок

решения задач графическим методом описы-

вается ниже в контексте задачи, связанной с деятельно-

стью компании

Риск

and

Pawn,

специализированной на

производстве хоккейных клюшек и наборов шахмат. Каж-

дая клюшка приносит компании прибыль в размере 2

долл., а каждый шахматный набор — 4 долл. На изготов-

ление одной клюшки требуется четыре часа работы на

участке А и два часа на участке В. Шахматный набор из-

готавливается с затратами шести часов работы на

участ-

ке А, шести часов на участке В и одного часа на

участ-

ке С. Доступная производственная мощность (Capacity

Available),

выраженная в рабочих часах, участка А состав-

ляет максимум 120 часов в день; участка В — 72 часа, а

участка С— 10 часов.

Вопрос: сколько клюшек и шахматных наборов долж-

на

выпускать в день компания, чтобы получать макси-

мальную прибыль?

1. Сформулируйте задачу с использованием математиче-

ских символов. Если обозначить количество хоккейных

клюшек через Я, а количество шахматных наборов — G, то

целевую функцию

(Objective

Function) для достижения мак-

симальной прибыли можно выразить следующим образом.

Максимизировать Z = $2# + $4(7;

при

условии следующих ограничений по мощностям:

(1) 4Я + 6G £ 120 (ограничение по

участку

А);

(2) 2# + 6

£ 72 (ограничение по

участку

В);

(3) 1G £ 10 (ограничение по

участку

при условии, что Я, G > 0.

Такая

формулировка удовлетворяет всем пяти услови-

ям,

предъявляемым к задачам линейного программирова-

ния,

описанным ниже.

1. Речь идет об ограниченных ресурсах (конечное чис-

ло рабочих часов по каждому из участков).

2. Точно сформулирована целевая функция (известны

значения

каждой переменной и цель задачи).

3. Все уравнения носят линейный характер (в них от-

сутствуют

экспоненты и комбинационные состав-

ляющие).

4. Ресурсы однородны (для их оценки использована

одна и та же единица измерения, т.е. рабочее время).

5. Искомые переменные — делимые и неотрицательные

значения

(можно изготовлять и части хоккейной

клюшки или шахматного набора; однако не забывайте,

что если такой подход нежелателен, то

следует

восполь-

зоваться методом целочисленного программирования).

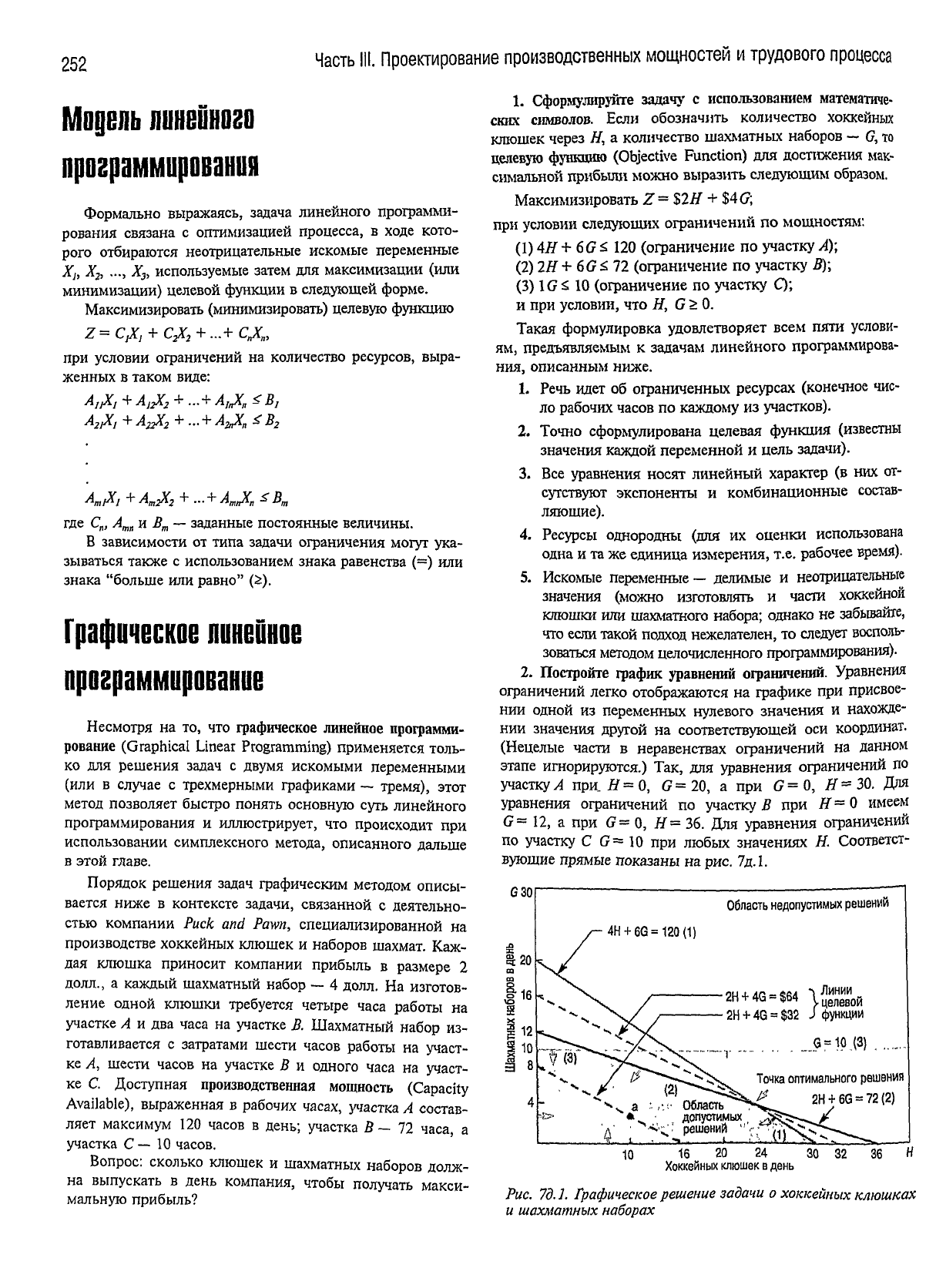
2. Постройте график уравнений ограничений. Уравнения

ограничений легко отображаются на графике при присвое-

нии

одной из переменных нулевого значения и нахожде-

нии

значения другой на соответствующей оси координат.

(Нецелые части в неравенствах ограничений на данном

этапе игнорируются.) Так, для уравнения ограничений по

участку

Л при. Я=0,

G=20,

а при G=0,

#=30.

Для

уравнения ограничений по

участку

В при Я= 0 имеем

G- 12, а при (?= 0, Я= 36. Для уравнения ограничений

по

участку

С G~ 10 при любых значениях Я. Соответст-

вующие прямые показаны на рис. 7д.1.

630

4H + 6G = 120(1)

Область

недопустимых решений

ои

х лп «й/1 "1

ЛИНИИ

2Н + 4G = $64

целевой

2Н + 4G = $32

функции

9=10.(3)

Точка

оптимального решения

2Н + 6G =

(2)

16 20 24 30 32 36 Н

Хоккейных клюшек

день

Рис. 7д.1.

Графическое

решение

задачи

хоккейных

клюшках

шахматных

наборах

Дополнение к главе 7. Линейное программирование

253

Пояснение

Пересечение ограничения (1) с осью G

Пересечение ограничения (1) с осью Н

Пересечение ограничения (2) с осью G

Пересечение ограничения (2) с осью Н

Пересечение ограничения (3) с осью G

Пересечение линии равной прибыли (целевой функции), соответствующей $32, с осью G

Пересечение линии равной прибыли, соответствующей $32, с осью Н

Пересечение линии равной прибыли, соответствующей

$64,

с осью G

Пересечение линии равной прибыли, соответствующей $64, с осью Н

120/4=30

72/2=36

32/2=16

64/2=32

120/6=20

72/6=12

32/4=8

64/4=16

3. Определите

допустимую

область. Направление знака

неравенства в каждом ограничении определяет область, в

которой

следует

искать допустимое решение. В данном

случае

все неравенства носят характер "меньше или рав-

но",

что означает, что недопустимо искать

любую

комби-

нацию

изделий, расположенную на графике справа и

сверху

от линий ограничений. Область допустимых реше-

ний

на графике рис.

7д.

закрашена серым и имеет форму

выпуклого многоугольника. Такой многоугольник бывает

выпуклым только при условии, что прямая линия, соеди-

няющая

любые две точки в нем, остается в его

пределах.

При

невыполнении данного условия задача либо непра-

вильно

сформулирована, либо не подлежит решению ме-

тодом линейного программирования.

4. Постройте график целевой функции. Целевая функ-

ция

отображается на графике следующим образом. Задай-

те какую-то произвольную величину общей прибыли и

найдите отрезки на осях координат, отсекаемые целевой

функцией,

как это было сделано для уравнений ограни-

чений.

Целевую функцию в данном контексте часто на-

зывают

линией

равной

прибыли,

или

линией

равносильного

вклада,

поскольку она отображает все возможные комби-

нации

двух

видов продукции для заданной прибыли. Так,

например,

на штриховой прямой, на графике ближе

всех

расположенной

к началу координат, мы можем опреде-

лить все возможные комбинации хоккейных клюшек и

шахматных наборов, которые

дадут

прибыль в 32 долл.,

выбрав для этого

любую

точку на прямой и найдя соот-

ветствующие количества каждого из производимых изде-

лий

по ее координатам. Так, для точки а комбинация, ко-

торая принесет компании прибыль в 32 долл.,

будет

клюшек

и 3 набора. Этот

результат

можно проверить под-

становкой

полученных с помощью графика значений

Н- 10, G - 3 в уравнение целевой функции:

($2 х 10) + ($4 х 3) = $20 + $12 = $32.

5. Найдите оптимальную точку. Можно математически

доказать, что оптимальная комбинация искомых пере-

менных

всегда

находится в крайней (угловой) точке вы-

пуклого многоугольника. На графике рис. 7д,1 таких то-

чек

четыре (исключая точку начала оси координат), и для

определения того, какая из них оптимальная,

существует

два способа. Первый заключается в алгебраическом поис-

ке

решений для разных вершин многоугольника и оты-

скании

среди них вершины с максимальной прибылью.

Такой

метод предполагает одновременное решение урав-

нений

для разных пар пересекающихся прямых и подста-

новку полученных параметров переменных в

целевую

функцию.

Так, например, вычисления для пересечения

линий

2Н + 6(7 = 72 и

= 10

будут

следующими.

Поставив

<?= 10 в 2#+ 6G = 72, получаем

2Я+(6х 10) = 72.

Следовательно, 2#= 12, а Н— 6. Подставив в

целевую

функцию

значения Н= 6 и

= 10, получаем

прибыль = $2Я

$4G = ($2 х 6) + ($4 х 10) =

$12 + $40 = $52.

Этот метод можно немного видоизменить, взяв пара-

метры Н и G непосредственно из графика и подставляя их

целевую

функцию, как это делалось в процессе преды-

дущих

вычислений. Недостаток данного

подхода:

при ре-

шении

задач с большим количеством ограничительных

уравнений возможных точек для оценки бывает очень

много,

и процедура математического тестирования каж-

дой из них становится просто неэффективной.

Второй метод, который обычно предпочитают специа-

листы, заключается в непосредственном поиске опти-

мальной

точки на линии равной прибыли. Эта процедура

состоит в том, что на графике проводится прямая,

парал-

лельная

любой произвольно выбранной исходной прямой

равной

прибыли, но наиболее удаленной от начала коор-

динат графика в пределах области допустимых значений.

(В

задачах

на минимизацию затрат прямая равной при-

были должна проходить через точку,

самую

близкую к на-

чалу

координат.) На рис. 7д.1 крайнюю

(угловую)

точку

пересекает штриховая линия, соответствующая уравнению

$2#+

$4(?= $64. Обратите внимание, что исходная про-

извольно выбранная прямая равной прибыли обязательна,

поскольку она отображает

угол

наклона целевой функции

для конкретной задачи

Это очень важно, так как при

другой

целевой функции

(например,

попробуйте подставить в значение прибыли

Угол

наклона целевой функции определяется коэффициентом,

который

в данном примере равен —2. Обозначив прибыль через

Р, имеем

Р=$2Я+$4О;

$2//=

Р-$4G,

H=pl2-2G.

Из этого

следу-

ет, что значение коэффициента наклона равно —2.

254

Часть

III. Проектирование производственных мощностей и трудового процесса

ЗЯ+Зб)

наиболее удаленной от начала оси координат

может быть другая точка. При условии, что уравнение

$2# + $4(7 = $64 является оптимальным, значение каж-

дой переменной, указывающее, какое количество изделий

следует

производить, можно определить по графику для

оптимальной точки: 24 хоккейные клюшки и 4 шахмат-

ных набора. Любые

другие

комбинации

дадут

компании

меньшую прибыль.

Симплексный

метод

Симплексный

метод (Simplex Method) представляет ал-

гебраическую процедуру, в результате которой аналитик,

последовательно выполняя ряд повторяющихся операций,

прогрессивно приближается к оптимальному решению

Теоретически данным методом можно решать задачи,

включающие любое количество переменных и ограниче-

ний,

но если в них, например, больше четырех перемен-

ных или ограничений, то вычисления лучше проводить на

компьютере. И все же для того, чтобы знать, как состав-

ляются уравнения, которые надо вводить в компьютерную

программу, и уметь эффективно использовать итоги, по-

лученные в результате работы в этой программе, предла-

гаем вам выполнить всю процедуру использования сим-

плексного метода без помощи компьютерной техники.

Шесть

этапов

симплексного

метода

Симплексный

метод включает в себя ряд отдельных

этапов.

Все они подробно описаны и подытожены в конце

данного раздела. Для наглядной демонстрации процедуры

поиска

решения симплексным методом воспользуемся все

той же задачей определения оптимальных объемов произ-

водства хоккейных клюшек и наборов шахмат.

Этап 1. Сформулируйте

задачу.

Вспомните, что, если

цель состоит в максимизации прибыли, то мы имеем та-

кие

условия задачи.

Максимизировать Z =

%2Н

+ $4(7;

при

условии, что

4Я + 6(7 й 120 (ограничение по участку А);

1Н + 6(7 £ 72 (ограничение по участку Б);

1G £ 10 (ограничение по участку Q;

Н,С>0

(требование отсутствия отрицательных значений).

Этап 2. Составьте исходную таблицу со свободными пе-

ременными.

При использовании симплексного метода не-

обходимо выполнить две следующие серьезные корректи-

ровки

задачи:

• ввести свободные переменные и

• построить таблицу решений.

Термин "симплексный" произошел отнюдь не от английского

слова

simple

(простой, простая). Он заимствован из «-мерной

геометрии.

Введение

свободных

переменных.

В каждое уравнение

ограничения вводятся свободные переменные. Свободная

переменная (Slack

Variable),

которая на практике может

рассматриваться как неиспользуемый ресурс, с математи-

ческой точки зрения представляет собой значение, необ-

ходимое для уравнивания

двух

частей ограничительного

уравнения.

Иными

словами, она предназначена для пре-

образования неравенства в равенство. Для рассматривае-

мой нами задачи потребуется ввести три свободные пере-

менные:

S, — для первого уравнения ограничений, S

—

для второго и S

— для третьего.

В результате наши уравнения примут следующий вид:

4H+6G+IS,= 120;

2H+6G+

=72;

1(7+

1S,= 10.

Чтобы в каждом уравнении ограничений были пред-

ставлены все свободные переменные, все они включаются

уравнения с множителями, равными нулю. В результате

такой корректировки получаем

следующую

систему урав-

нений:

4H+6G+

IS,

+0S

OS,

= 120;

2Я

05/

+ IS

+ OS,

= 72;

ОН +1G + OS, +0S

+ \Sj = 10.

Обратите внимание, что в третье уравнение введена

переменная Н с нулевым множителем. В целевую функ-

цию также добавляются свободные переменные, но по-

скольку они

никак

не влияют на прибыль, их множители

равны $0:

Z= $2# + $4(7 + OS; +0S

+ 0S

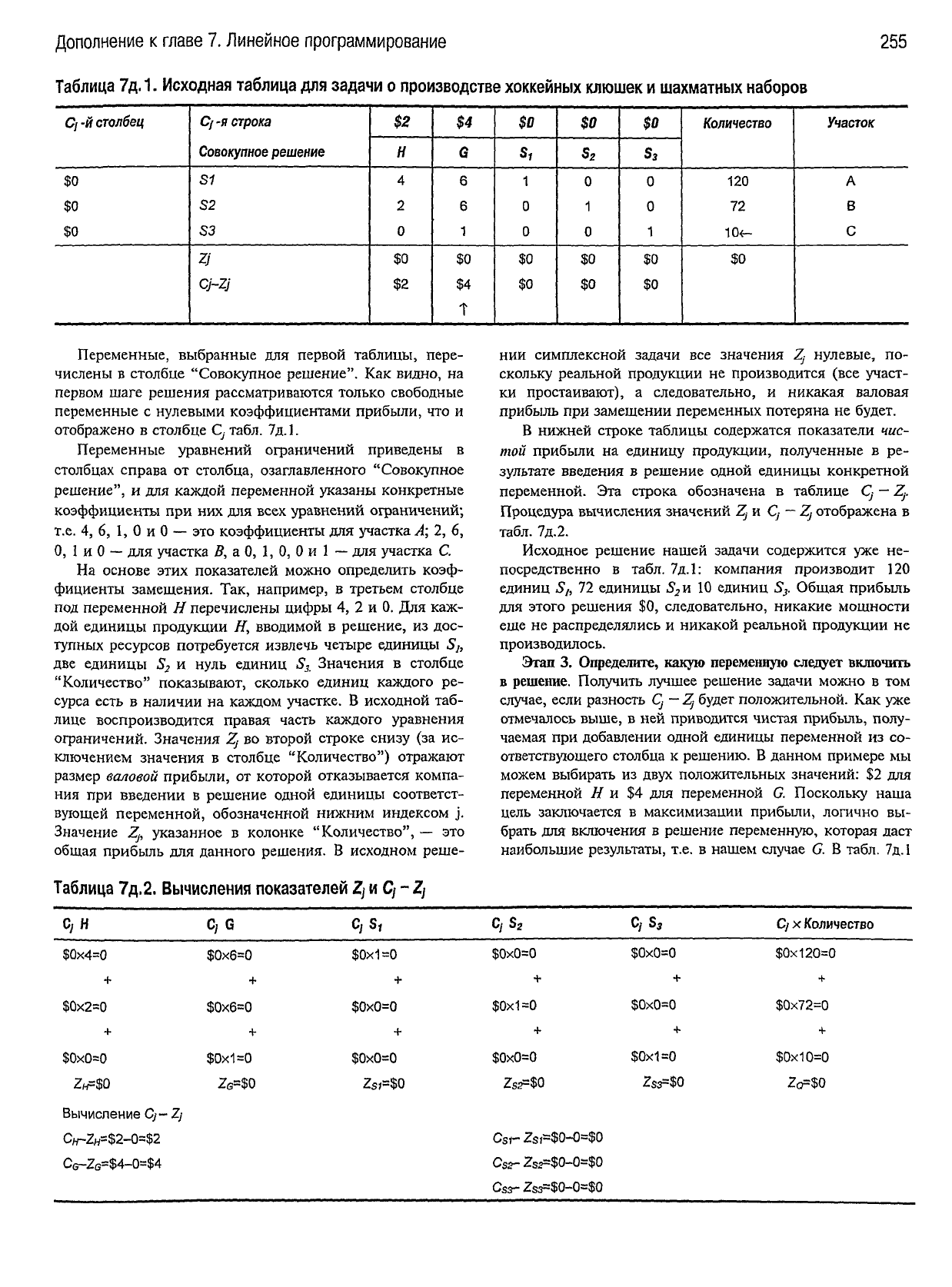
Построение

исходной

таблицы.

Исходная таблица

(табл. 7д.1) представляет удобный способ подготовки за-

дачи к решению с применением симплексного метода.

В данной таблице представлены.

1. Свободные переменные поэтапного решения.

2. Прибыль, соответствующая решению.

3. Переменная (если таковая существует), которая при

вводе в решение больше

других

увеличивает прибыль.

4. Показатель приведения переменных в решении (при

вводе одной единицы каждой переменной). Этот по-

казатель называется

коэффициентом

замещения.

5. Стоимость добавленной единицы ресурса (например,

часа), которую называют

теневой

ценой.

Первые четыре характеристики мы обсудим сейчас, в

ходе

описания табл. 7д.1, а о последней поговорим под-

робнее дальше в этом дополнении к главе.

В верхней строке табл. 7д.1 содержатся значения С

}

(вклад в общую прибыль, соответствующий выпуску одной

единицы каждого вида продукции). В этой строке приведе-

ны

множители переменных целевой функции. Они остают-

ся

неизменными во всех последующих расчетных таблицах.

В первом столбце, озаглавленном С

}

, для удобства приведе-

ны

значения прибыли на единицу переменных, включен-

ных в решение на каждом этапе решения задачи.

Дополнение

главе 7. Линейное программирование

Таблица

7д.1.

Исходная таблица для задачи

производстве хоккейных клюшек и шахматных наборов

255

Cj -й

столбец

С/

-я

строка

Совокупное

решение

Cj-Zj

Количество

120

10<-

Участок

Переменные,

выбранные для первой таблицы, пере-

числены в столбце "Совокупное решение". Как видно, на

первом шаге решения рассматриваются только свободные

переменные с нулевыми коэффициентами прибыли, что и

отображено в столбце С

табл. 7д. 1.

Переменные уравнений ограничений приведены в

столбцах справа от столбца, озаглавленного "Совокупное

решение", и для каждой переменной указаны конкретные

коэффициенты

при них для

всех

уравнений ограничений;

т.е. 4, 6, 1, 0 и 0 — это коэффициенты для участка А; 2, 6,

0, 1 и 0 — для участка В, а 0, 1, 0, 0 и 1 — для участка С.

На

основе этих показателей можно определить

коэф-

фициенты

замещения. Так, например, в третьем столбце

под переменной Н перечислены цифры 4, 2 и 0. Для каж-

дой единицы продукции Я, вводимой в решение, из дос-

тупных ресурсов потребуется извлечь четыре единицы S

две единицы S

и нуль единиц S

. Значения в столбце

"Количество" показывают, сколько единиц каждого ре-

сурса

есть в наличии на каждом участке. В исходной таб-

лице воспроизводится правая часть каждого уравнения

ограничений. Значения Z

во второй строке снизу (за ис-

ключением значения в столбце "Количество") отражают

размер

валовой

прибыли, от которой отказывается компа-

ния

при введении в решение одной единицы соответст-

вующей переменной, обозначенной нижним индексом j.

Значение Z

указанное в колонке "Количество", — это

общая прибыль для данного решения. В исходном реше-

Таблица

7д,2.

Вычисления

показателей

С;

2у

нии

симплексной задачи все значения Zj нулевые, по-

скольку реальной продукции не производится (все

участ-

ки

простаивают), а следовательно, и никакая валовая

прибыль при замещении переменных потеряна не

будет.

В нижней строке таблицы содержатся показатели чис-

той прибыли на единицу продукции, полученные в ре-

зультате

введения в решение одной единицы конкретной

переменной.

Эта строка обозначена в таблице Су

—

Zj.

Процедура вычисления значений 2J и C

—

Zj отображена в

табл. 7д.2.

Исходное решение нашей задачи содержится уже не-

посредственно в табл. 7д.1: компания производит 120

единиц S

72 единицы

10 единиц 5,. Общая прибыль

для этого решения $0, следовательно, никакие мощности

еще не распределялись и никакой реальной продукции не

производилось.

Этап

Определите,

какую

переменную

следует

включить

решение.

Получить

лучшее

решение задачи можно в том

случае,

если разность Cj

— Z/

будет

положительной. Как уже

отмечалось выше, в ней приводится чистая прибыль, полу-

чаемая при добавлении одной единицы переменной из со-

ответствующего

столбца к решению. В данном примере мы

можем выбирать из

двух

положительных значений: $2 для

переменной Я и $4 для переменной G. Поскольку наша

цель заключается в максимизации прибыли, логично вы-

брать для включения в решение переменную, которая

даст

наибольшие результаты, т.е. в нашем

случае

G. В табл. 7д.

С; Н

С; G

c,s,

Cj x Количество

$0x4=0 $0x6=0

$0x1=0

$0x0=0

$0x120=0

$0x2=0 $0x6=0

$0x0=0

$0x1=0

$0x0=0

$0x72=0

$0x0=0

Z«=$0

Вычисление

Cj-

Z-,

Cw-Z

=$2-0=$2

Cer-Z

=$4-0=$4

$0x1=0

=$0

$0x0=0

,=$0

$0x0=0

2=$0

Csr- Zsf=$0-0=$0

Car Zs2=$0-0=$0

Css- Zs3=$0-0=$0

$0x1=0

$0x10=0

Zo=$0

256

Часть

III. Проектирование производственных мощностей и трудового процесса

столбец для этой переменной помечен маленькой стрелкой,

расположенной под ним. (Для достижения каждого

улуч-

шенного решения одновременно можно добавлять только

одну переменную.)

Этап 4. Определите, какую переменную

следует

заме-

нить.

В решение рациональнее ввести переменную G, сле-

дующим шагом

будет

выбор переменной, подлежащей за-

мене.

Для этого разделим каждое значение столбца

"Количество" на соответствующее ему значение в столбце

G и выберем переменную, которая

даст

наименьшее по-

ложительное значение. Именно она и

будет

замещена.

Для строки S/. 120/6 = 20.

Для строки S? 72/6 - 12.

Для строки S

: 10/1 = 10.

Поскольку наименьшим значением является 10, нам

следует

заместить переменную S

. В табл. 7д.1 строка для

этой

переменной помечена маленькой стрелкой, распо-

ложенной в правой части таблицы. Это максимальное

значение G, которое может быть включено в решение.

Другими словами, выпуск более чем 10 единиц G превы-

сит имеющиеся в наличии производственные мощности

участка С. Этот

результат

можно проверить математиче-

ски,

рассмотрев ограничение G£ 10, или визуально, ис-

следовав графическое отображение задачи, показанное на

рис.

7д.1. Из этого графика также видно, что 20 и 12 —

это значения G для

двух

других

ограничений, и если ог-

раничение G^ 10 удалить, то в решение можно было бы

дополнительно ввести 2 единицы G.

Этап 5. Вычислите новые значения строки для вводимой

переменной.

Для введения в решение переменной G

требу-

ется замещение всей строки S? Значения G для замещения

строки

получают

делением каждого текущего значения S

на

значение в столбце G, соответствующее данной строке.

Это значение называют

элементом

пересечения

(Intersectional Element), поскольку оно находится на пере-

сечении строки и столбца. Эту перекрестную взаимосвязь

выделяют из остальной таблицы, после чего выполняют все

необходимые операции деления, как показано в табл. 7д.З.

Таблица

7д.З.

Вычисление

новых

значений строки для

вводимой переменной

0 1 0 0 1 10

0/1=0,1/1

=1,0/1

=0,

0/1=0,1/1

1,10/1

= 10

Этап 6. Проверьте остальные строки. Новые значения

третьей строки (теперь относящиеся к переменной G) та-

ковы:

0, 1, 0, 0, 1 и 10. В нашем

случае

они совпадают со

старыми показателями третьей строки таблицы.

Введение в

задачу

новой переменной влияет на значе-

ния

остальных переменных, и для обновления таблицы не-

обходимо провести второй тур вычислений. В нашем слу-

чае мы хотим определить, как влияет введение переменной

G на строки S, и S? Такие расчеты выполняются с исполь-

зованием метода, получившего название метода рычага

(Pivot Method), либо алгебраической подстановкой. Первый

метод представляет собой больше механическую процедуру

широко используется на практике, а второй чаще приме-

няется

для объяснения логики процесса обновления. Про-

цедура

использования метода рычага для получения новых

значений

S, и S

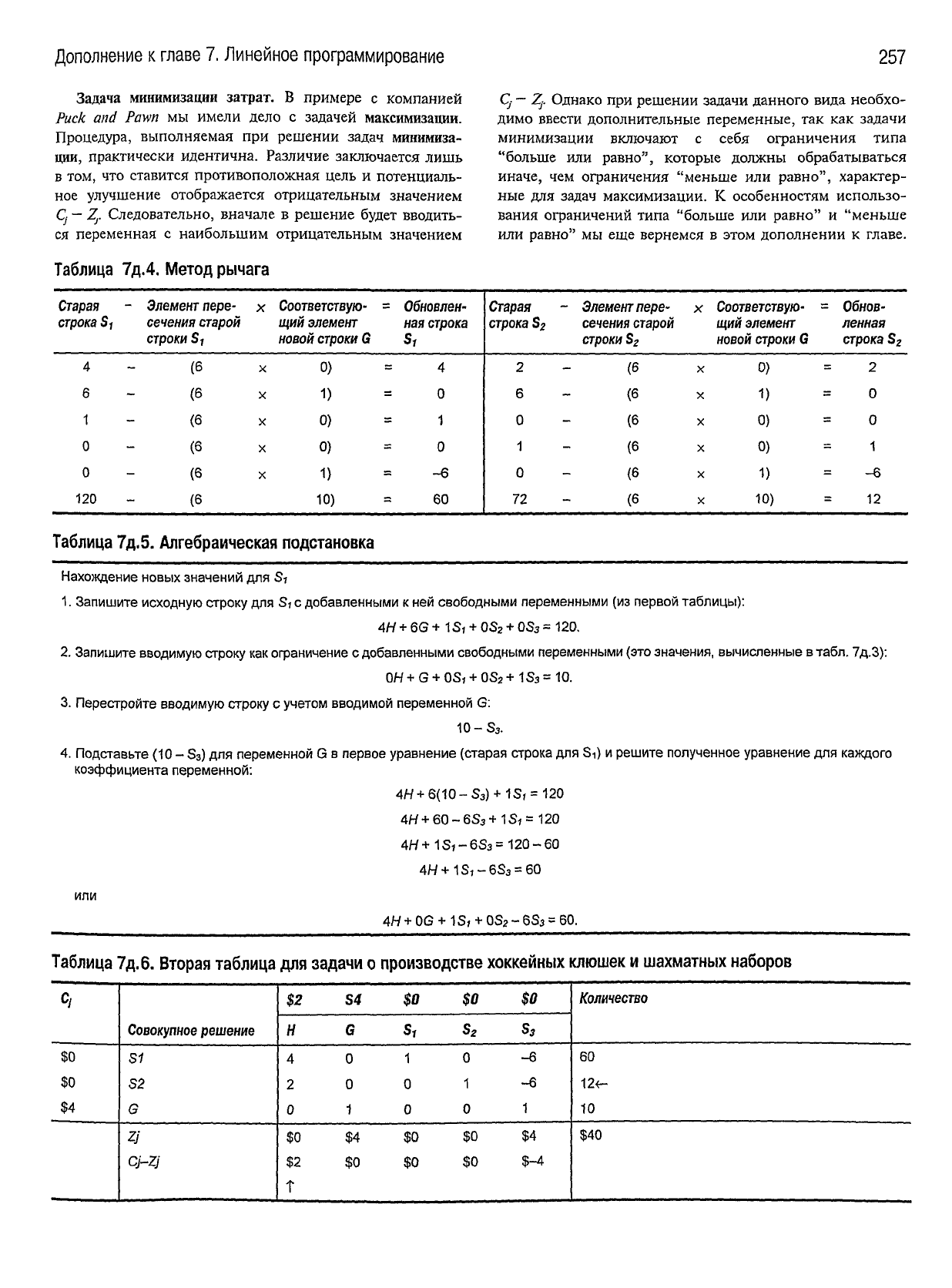
отображена в табл. 7д.4. (По сути, данный

метод заключается в вьнитании умноженных на 6 значений

строки 3 из строк S] и 5г.)

Коррекция

таблицы алгебраической подстановкой за-

ключается в подстановке всего уравнения для вводимой

строки во все остальные строки и решение его для

всех

из-

мененных значений переменной каждой строки. Процеду-

ра, представленная в табл. 7д.5, показывает, что решение

задачи линейного программирования симплексным мето-

дом по

сути

сводится к решению системы уравнений.

Выделив множители у переменных для новой строки

S, из табл. 7д.5, получаем такие же значения, как и при

использования метода рычага: 4, 0, 1, 0, —6, 60.

Результаты вычислений на этапах с

третьего

по шестой

вместе с вычислениями Z

и Cj-Z

}

отображены в

табл. 7д.6. Воспользовавшись терминологией, принятой в

математическом программировании, можно сказать, что

мы закончили первую

итерацию

поиска решения задачи.

Оценивая

полученное решение,

следует

обратить осо-

бое внимание на два момента: прибыль составляет

40 долл., но важнее то, что возможно дальнейшее

улуч-

шение этого показателя, поскольку в строке Cj -Zj мы

имеем положительное значение.

Вторая

итерация.

Поскольку переменная Н имеет наи-

больший показатель Cj - Z

}

= 2, она и

будет

вводиться. За-

меняемой переменной

будет

, так как при делении зна-

чений

из столбца "Количество" на соответствующие им

значения

из столбца Н она получит наименьшее значение:

S, = 60/4 = 14; S

= 12/2 = 6; S

= 10/0 = -.

Таким

образом, в строку Я

будут

введены следующие

значения:

2/2 = 1, 0/2 = 0, 0/2 = 0, 1/2 = 1/2, -6/2 = -3, 12/2 = 6.

Откорректированная в табл. 7д.7 строка S;.

0, 0, 1, -2, 6, 36.

Откорректированная в табл. 7д.7 строка G:

0, 1, 0, 0, 1, 10.

Воспользовавшись результатами табл. 7д.7, построим

третью

табл. 7д.8.

Анализируя табл. 7д.8, мы видим, что, введя макси-

мальное значение S

(что технически вполне осуществи-

мо),

можно достичь дальнейшего улучшения. Из расчетов

нижней части табл. 7д.8 получаем, что вследствие огра-

ничения

по показателю Sj максимальное значение S

, ко-

торое можно

будет

ввести в решение, составляет шесть

единиц.

Заменив показатель S, показателем S

и проведя

корректировку, составляем табл. 7д.9.

Поскольку строка С

;

- Zj содержит только отрицатель-

ные значения, дальнейшее улучшение невозможно, сле-

довательно, в

результате

трех

итераций мы достигли оп-

тимального решения (Я= 24, G- 4). Во врезке "Краткое

изложение этапов симплексного метода: задача на макси-

мизацию прибыли" вашему вниманию представлено

краткое изложение

всех

пройденных нами этапов.

Дополнение

к главе 7.

Линейное

программирование

257

Задача минимизации затрат. В примере с компанией

Риск

and

Pawn

мы имели

дело

с задачей максимизации.

Процедура, выполняемая при решении задач минимиза-

ции,

практически идентична. Различие заключается лишь

том, что ставится противоположная цель и потенциаль-

ное улучшение отображается отрицательным значением

—

Следовательно, вначале в решение

будет

вводить-

ся

переменная с наибольшим отрицательным значением

—

Zj. Однако при решении задачи данного вида необхо-

димо ввести дополнительные переменные, так как задачи

минимизации

включают с себя ограничения типа

"больше или равно", которые должны обрабатываться

иначе,

чем ограничения "меньше или равно", характер-

ные для задач максимизации. К особенностям использо-

вания

ограничений типа "больше или равно" и "меньше

или

равно" мы еще вернемся в этом дополнении к главе.

Таблица

Старая

строка

120

7д.4.

Метод

рычага

Элемент

пере-

сечения

старой

строкиS,

Соответствую-

щий

элемент

новой

строки

Ю)

Обновлен-

ная

строка

-6

Старая

строка

Элемент

пере-

сечения

старой

строки

Соответствую-

щий

элемент

новой

строки

10)

Обнов-

ленная

строка

-6

Таблица

7д.5.

Алгебраическая

подстановка

Нахождение

новых

значений

для Si

Запишите

исходную

строку

для

добавленными

к ней

свободными

переменными

(из

первой

таблицы):

4Я+ 6G + 1S, + 0$

+ 0S

= 120.

Запишите

вводимую

строку

как

офаничение

добавленными

свободными

переменными

(это

значения,

вычисленные

табл.

7д.З):

0H+G

0S,

+1S

=10.

Перестройте вводимую строку с учетом вводимой переменной

-S

Подставьте

(10

- S

) для

переменной

G в

первое

уравнение

(старая

строка

для S-0 и

решите

полученное

уравнение

для

каждого

коэффициента

переменной:

4Н+ 6(10-

) + 1S,= 120

4H+1S,-6S

120-60

4H+1S,-6S

= 60

или

4W +

-6S

Таблица

7д.6.

Вторая

таблица для

задачи

производстве

хоккейных

клюшек

и шахматных

наборов

С/

Совокупное

решение

Cj-Zj

-6

-б

$-4

Количество

12<-

$40

258

Часть

III.

Проектирование производственных мощностей

трудового процесса

Таблица

7д.7.

Корректировка строк

Старая

строка

-6

Элемент

пере-

сечения

старой

строки

Соответству-

ющий

элемент

новой

строки

1/2)

-3)

Новая

строка

—2

Старая

строка

Элемент пере-

сечения

старой

строки

Соответству-

ющий элемент

новой

строки

1/2)

-3)

Обнов-

ленная

строка

Таблица

7д.8.

Су

Третья

таблица

для

Совокупное

решение

Cj-Zj

задачи

производстве

хоккейных

клюшек

шахматных

наборов

-2

1/2

$-1

-3

$-2

Количество

36<-

$52

•—

36/6 =

6 6/-3

-2

(отрицательное

значение)

10/1

= 10

Поскольку

данной

задаче

три

уравнения

ограничений,

решении

должно

быть

три

переменные

неотрицательными

значениями

отрицательное

значение

нельзя

вводить

решение.

Таблица

7д.9.

Четвертая

таблица

для

задачи

производстве

хоккейных

клюшек

шахматных

наборов

(оптимальное

решение)

Су

Совокупное решение

Cj-Zj

1/6

1/2

-1/6

$1/3

$-1/3

-1/3

-1/2

1/3

$1/3

$-1/3

Количество

$64

Определение

пути

поиска

решения при

симплексном

методе

Как

уже отмечалось выше, оптимальное решение для

задач линейного программирования получают нахождением

экстремальной угловой точки. Симплексная процедура на-

чинается с получения исходного решения, за которым сле-

дует

поиск следующего наиболее выгодного и "переска-

кивание"

с одной точки пересечения прямых на

другу

(или,

случае

с многомерным пространством, от одного

пересечения плоскостей на другое). Оценка угловой точки

выполняется в

результате

одной итерации, и, достигнув

наиболее удаленной точки (в

случае

с задачами на макси-

мизацию прибыли на этапе, когда следующая за ней точка

отображает снижение прибыли), вы получаете оптимальное

решение.

Дополнение

к главе 7.

Линейное

программирование

259

Краткое изложение этапов симплексного метода: задача на максимизацию

приОыли

1. Сформулируйте

задачу:

определите целевую функцию и наметьте ограничения.

2. Постройте исходную таблицу со свободными переменными в совокупном решении и вычислите стро-

ки

Zj и Cj

—

3. Определите, какую переменную

следует

ввести в решение (наибольшее значение С

- Zj).

4. Определите, какую переменную

следует

заменить (по наименьшему положительному коэффициенту,

получаемому делением значений столбца "Количество" на соответствующее ему значение из столбца,

выбранного на этапе 3).

5. Вычислите новые значения строки для ввода переменной и вставьте в таблицу новую строку (строка,

подлежащая замене, плюс элемент пересечения).

6. Откорректируйте остальные строки и введите их в новую таблицу; вычислите новые значения для

строк

—

Zj (показатели исходных строк, минус элемент пересечения из исходной строки, умно-

женный

на соответствующий ему элемент из новой строки). Если в

результате

вы не получаете ни од-

ного положительного значения С

Zj,

значит, данное решение

будет

оптимальным. Если же такое

значение

есть, повторите этапы с 3 по 6.

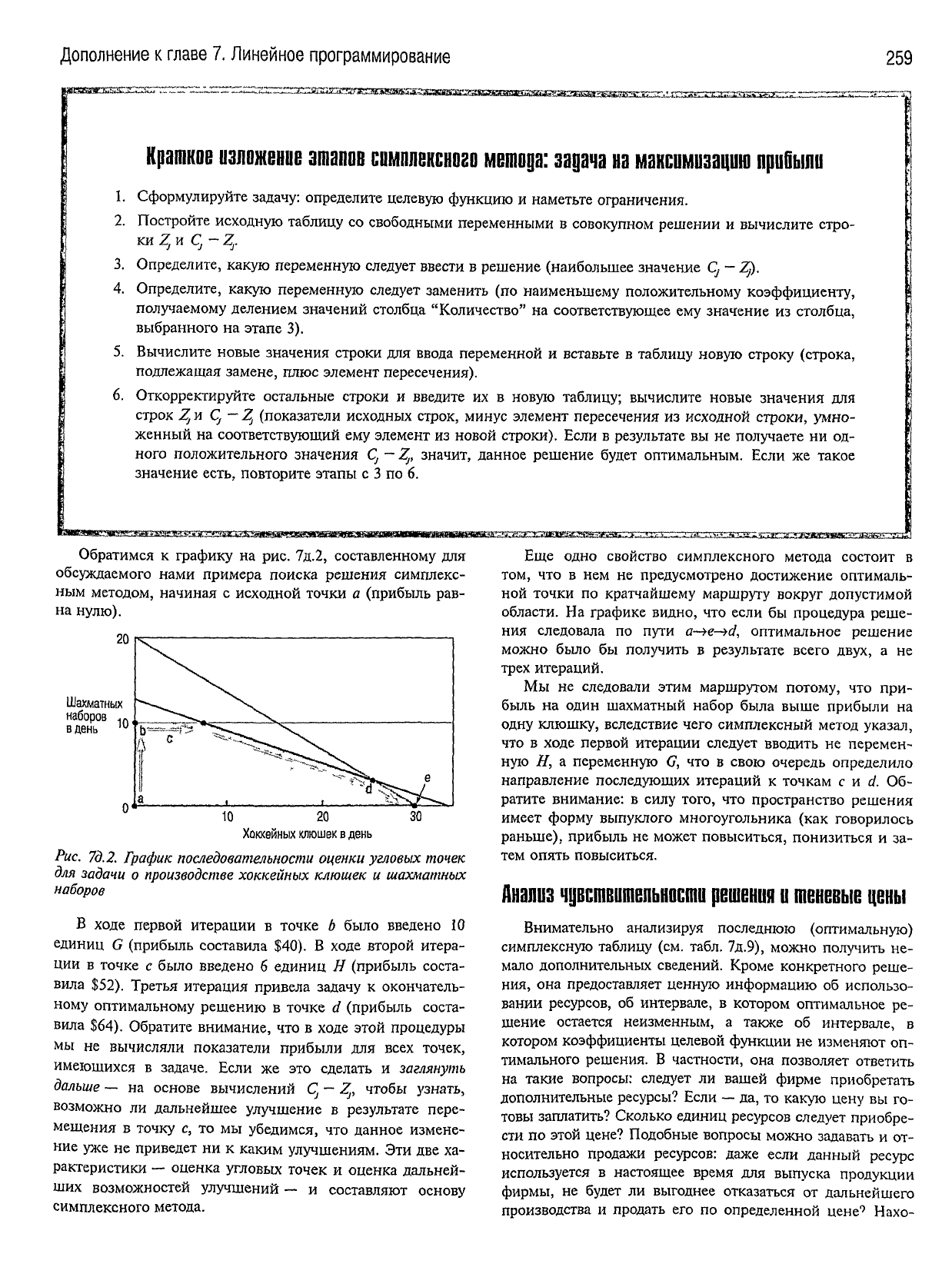
Обратимся к графику на рис. 7д.2, составленному для

обсуждаемого нами примера поиска решения симплекс-

ным

методом, начиная с исходной точки а (прибыль рав-

на

нулю).

Шахматных

наборов

вдень

Хоккейных клюшек в день

Рис. 7д.2.

График

последовательности

оценки

угловых

точек

для

задачи

производстве

хоккейных

клюшек

шахматных

наборов

ходе

первой итерации в точке b было введено 10

единиц

G (прибыль составила $40). В

ходе

второй итера-

ции

в точке с было введено б единиц Н (прибыль соста-

вила $52). Третья итерация привела задачу к окончатель-

ному оптимальному решению в точке d (прибыль соста-

вила $64). Обратите внимание, что в

ходе

этой процедуры

мы

не вычисляли показатели прибыли для всех точек,

имеющихся в задаче. Если же это сделать и

заглянуть

дальше

— на основе вычислений C

— Zj,

чтобы

узнать,

возможно ли дальнейшее улучшение в

результате

пере-

мещения

в точку с, то мы убедимся, что данное измене-

ние

уже не приведет ни к каким улучшениям. Эти две ха-

рактеристики

— оценка

угловых

точек и оценка дальней-

ших возможностей улучшений — и составляют основу

симплексного

метода.

Еще

одно свойство симплексного метода состоит в

том, что в нем не предусмотрено достижение оптималь-

ной

точки по кратчайшему маршруту вокруг допустимой

области. На графике видно, что если бы процедура реше-

ния

следовала по пути

a—^e—^d,

оптимальное решение

можно было бы получить в

результате

всего

двух,

а не

трех

итераций.

Мы

не следовали этим маршрутом потому, что при-

быль на один шахматный набор была выше прибыли на

одну клюшку, вследствие чего симплексный метод указал,

что в

ходе

первой итерации

следует

вводить не перемен-

ную Н, а переменную G, что в свою очередь определило

направление

последующих итераций к точкам с и d. Об-

ратите внимание: в силу того, что пространство решения

имеет форму выпуклого многоугольника (как говорилось

раньше),

прибыль не может повыситься, понизиться и за-

тем опять повыситься.

Анализ

чувствительности

решения и теневые

цены

Внимательно анализируя последнюю (оптимальную)

симплексную таблицу (см. табл. 7д.9), можно получить не-

мало дополнительных сведений. Кроме конкретного реше-

ния,

она предоставляет ценную информацию об использо-

вании

ресурсов, об интервале, в котором оптимальное ре-

шение

остается неизменным, а также об интервале, в

котором коэффициенты целевой функции не изменяют оп-

тимального решения. В частности, она позволяет ответить

на

такие вопросы:

следует

ли вашей фирме приобретать

дополнительные ресурсы? Если — да, то какую цену вы го-

товы заплатить? Сколько единиц ресурсов

следует

приобре-

сти по этой цене? Подобные вопросы можно задавать и от-

носительно продажи ресурсов:

даже

если данный ресурс

используется в настоящее время для выпуска продукции

фирмы,

не

будет

ли выгоднее отказаться от дальнейшего

производства и продать его по определенной цене

Нахо-

260

Часть

III. Проектирование производственных мощностей и трудового процесса

дить правильные ответы на такие вопросы очень важно, и

симплексный метод позволяет это делать. Причем эти отве-

ты

дополняют

оптимальное решение, вычисленное в соот-

ветствии с целевой функцией в табл. 7д.9.

Кроме перечисленных выше вопросов, можно задать и

такой вопрос: если мы изменим прибыль на единицу про-

дукции (изменив коэффициент целевой функции), не при-

ведет

ли это к изменению оптимального решения? Оты-

скивая

на него ответ, мы имеем дело с анализом чувстви-

тельности

(Sensitivity

Analysis),

который заключается в опре-

делении того, насколько изменится решение в результате

некоторых изменений целевой функции, или наоборот, как

изменение решения повлияет на целевую функцию.

Вернемся к табл. 7д.9. Значения С

}

—

связанные со

свободными переменными, называют теневыми ценами

(Shadow Prices),

безубыточными

ценами,

предельными

зна-

чениями

или

приростными

значениями.

Обратите внимание,

теневые цены для S, и S

составляли $1/3 (или 33 цента)

каждая, а для S

— $0. При любом превышении этой це-

ны

управленческий персонал

будет

стремиться к продаже

ресурсов, а при понижении ниже этого уровня — приоб-

рести их. А теперь предлагаем вам еще раз рассмотреть,

как

решается эта задача, на этот раз с применением дос-

тупной компьютерной техники.

Решение

задач линейного программирования

в MS Excel

Для решения задач линейного программирования час-

то используются электронные таблицы. В большинство

таких таблиц встроены понятные и простые в примене-

нии

стандартные программы В программе Microsoft

Excel, например, есть оптимизирующий инструмент

Solver

(Поиск решения), работу которого мы продемонст-

рируем опять же для решения задачи о производстве хок-

кейных клюшек и шахмат. Программа

Solver

(Поиск ре-

шения)

запускается из меню Tools (Сервис), после чего

появляется диалоговое окно, запрашивающее информа-

цию,

необходимую для ее работы.

Вначале нужно поставить

задачу,

указав целевую ячей-

ку (или целевую функцию), изменяемые ячейки (искомые

переменные) и ячейки ограничений. На рис. 7д.З изобра-

жена электронная таблица с информацией, которая необ-

ходима для решения данной задачи

Поле Target Cell (Установить целевую ячейку) (в нашем

случае

ячейка D5) содержит формулу, умножающую ко-

личество произведенных клюшек и шахматных наборов

на

соответствующую им прибыль; значения, указанные в

поле Changing

Cells

(Изменяя ячейки), соответствуют иско-

мым переменным задачи. В поле Subject to Constraints

(Ограничения) указаны ячейки для введения конкретных

ограничений на решение. Обратите внимание, что в диа-

логовом окне

Solver

(Поиск решения) необходимо указать,

что наши значения для решения должны быть больше

или

равны нулю.

На

рис. 7д.З не показано диалоговое окно Options

(Параметры), но если его вывести на экран, то появится

поле, в котором можно указать, что данная задача являет-

ся

линейной, что позволяет значительно ускорить процесс

ее решения В этом окне, которое управляет механизмом

поиска

решения, используемым программой

Solver

(Поиск

решения),

можно выбрать и многие

другие

варианты.

Данная

программа способна решать задачи с использова-

Hochey

Sticks

Chess

Sets'

used

I Capacity

';()<='

УХУ

Щ'- 72;

Рис 7д.З.

Поиск

решения

задачи

(Solver)

программе

Microsoft

Excel