Циценкова Г.А., Чукавина Т.В., Рязанова Л.Д., Труппова В.А. Методические указания и контрольные задания по высшей математике
Подождите немного. Документ загружается.


101
5.3.
()
)34(
2222
3
22
yxxayx +=+
5.4.
()
)23(
222
2
22
yxayx +=+
5.5.
)3(
2224
yxax −=
5.6.
)(
4426
yxax −=
5.7.
)3(
2224
yxax −=
5.8.
(
)
4426
xyay −=
5.9.
()
)32(
222
2
22
yxayx +=+
5.10.
)3()(
222226
xyyxay −⋅+=
Задача 6
Вычислить с помощью тройного интеграла объем тела, ограниченного
указанными поверхностями. Сделать чертежи данного тела и его проекции на
плоскость
XOY
.
6.1.
,0=z
,x
z
=
,0
=
y
,4
=
y
.25
2
yx −=
6.2.
,0=z
,9
2
yz −=
.9
22
=+ yx
6.3.
,0=z
,4 yxz −−
=
.4
22
=+ yx
6.4.
,0=z
,
2
yz =
.9
22
=+ yx
6.5.
,0=z
,2=+ zy
.4
22
=+ yx
6.6.
,0=z
,4
2
yz =
,02
=
−
yx
.0
=
+
yx
6.7.
,0=z
,
22
yxz +=
.4
2
=+ yx

102
6.8.
,0=z
,1
2
yz −=
,
22
yx =
.12
2
+= yx
6.9.
,0=z
,1
2
xz −=
,0
=
y
.3 xy
−
=
6.10.
,0=z
,4 yz =
,0
=
x
.4
=
+
yx
Задача 7
Вычислить криволинейный интеграл. Сделать чертеж.
7.1.
∫
−−−
L
dyyxdxyx )()(
22
Вдоль дуги L окружности
tx cos5
=
,
ty sin5
=
, обходя ее против хода
часовой стрелки от А(5;0) до В(0;5).
7.2.
∫
−−+
L
dyyxdxyx )()(
вдоль ломанной L = ОАВ, где 0(0;0), А(2;0), В(4;5).
7.3.
∫
+
−
L
yx
xdyydx
22
вдоль границы L треугольника АВС, обходя ее против хода часовой стрелки,
если А(1;0), В(1;1), С(0;1).
7.4.
∫
−+−
L
dyxyydxxyx )2()2(
22
вдоль дуги L параболы
2
xy =
от точки А(-1;1) до точки В(1;1).
7.5.
∫
++−
L
dyyxydxxyx )2()3(
22
вдоль верхней половины L эллипса
tx cos3
=
,
ty sin3
=
.
7.6.
∫
+++
L
dyxydxyx )()(
22
вдоль ломанной L = АВС, где А(1;2), В(1;5), С(3;5).
103
7.7.
∫
+
L
dy
y
x
ydx
вдоль дуги L кривой
x
ey
−
=
от точки А(0;1) до точки В(-1;е).
7.8.
∫
−
+
L
dy
y
x
dx
y
y
2
2
1
вдоль отрезка L = АВ прямой от точки А(1;2) до точки В(2;4).
7.9.
∫
+−
L
xdydxxxy )(
2
вдоль дуги L параболы
2
xy =
от точки О(0;0) до точки А (1;2).
7.10.
∫
+
L
xdydx
x
y
вдоль дуги L кривой
xy ln=
от точки А(1;0) до точки В(е;1).
Задача 8.
Представить заданную функцию
)(zf
=
ω
, где
iyxz +
=
, в виде
),(),( yxivyxu +=
ω
; проверить является ли она аналитической. Если да, то
найти значение ее производной в заданной точке
0
z
.
8.1.
,)(
3
iz=
ω
.1
0
iz
+
−
=
8.2.
,
21 z
e
−
=
ω
.3
0
iz
π
=
8.3.
,2)1(
2
zzi −−=
ω
.1
0
=
z
8.4.
,
2
z
e
−
=
ω
.
0
iz =
8.5.
,3
3
izz −+=
ω
.
0
iz
−
=
8.6.
,
21 iz
e
−
=
ω
.6
0
π
=z
8.7.
,2
2
izz −=
ω
.1
0
iz
−
=
8.8.
,
2
iz
e=
ω
.2
0
iz
π
=
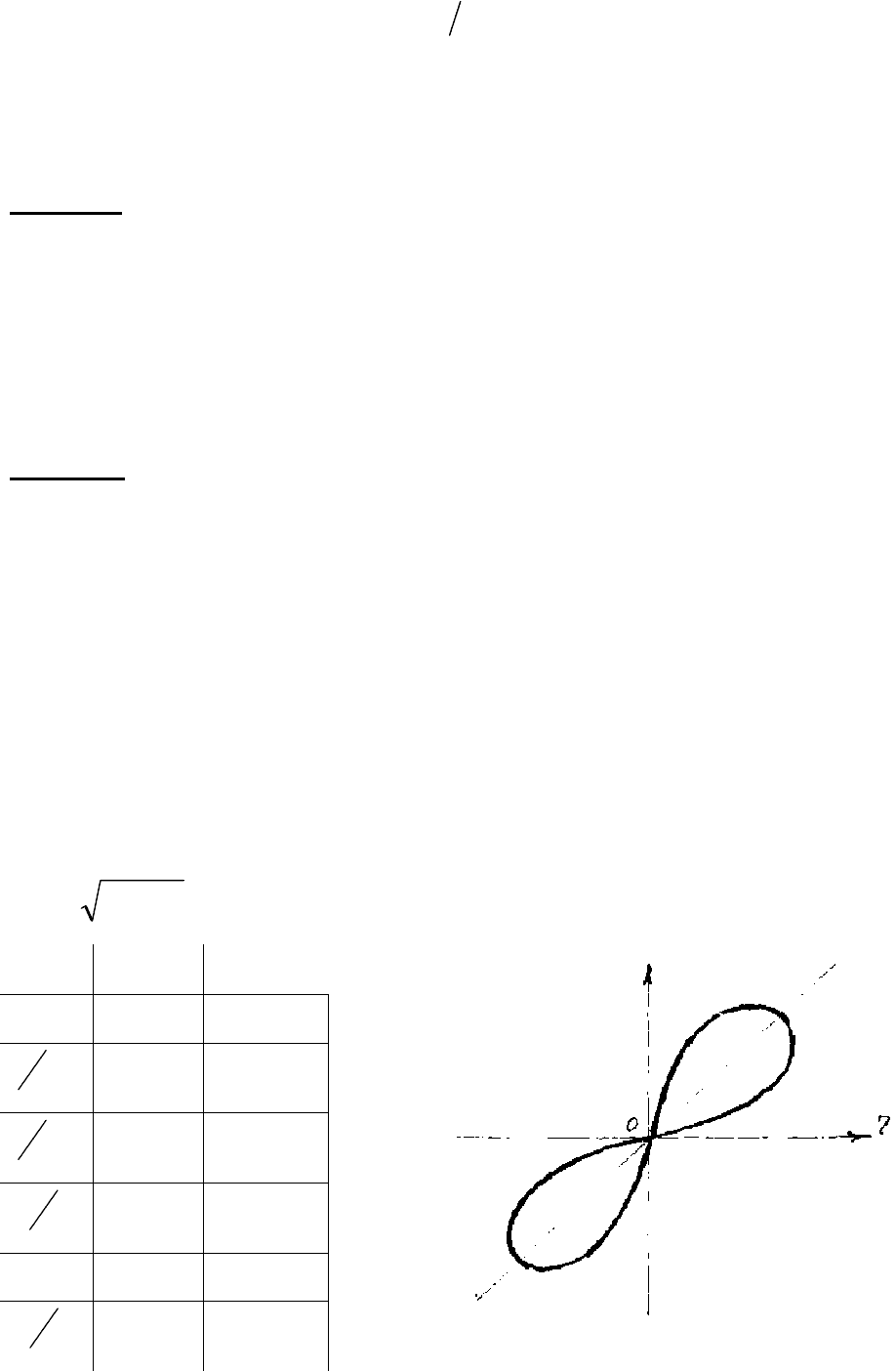
104
8.9.
,
23
izz ++=
ω
.32
0
iz
=
8.10.
,
z
ze=
ω
.1
0
π
iz
+
−=
Решение типового варианта
Задача 5.
Найти площадь фигуры, ограниченной кривой
xyayx
2222
2)( =+
с помощью
двойного интеграла в полярных координатах.
Решение.
Перейдем к полярным координатам, полагая в данном уравнении кривой
,cos
ϕ
r
x
=
,sin
ϕ
ry =
получим:
[]
,sincos2)sin(cos
22
2
222
ϕϕϕϕ
⋅=+ rar
ϕ
2sin
22
ar =
- полярное уравнение кривой. Эта кривая называется
«лемнискатой Бернулли». Построим эту кривую.
0 ,2sin >= aar
ϕ
ϕ
Sin 2
ϕ
r
0 0 0
4
π
1 а
2
π
0 0
4
3
π
-1 не сущ.
π
0 0
4
5
π
1 а
105
2
3
π
0 0
4
7
π
-1 не сущ.
4
8
π
0 0
Кривая симметрична относительно точки 0 и при измерении
ϕ
от 0 до
2
π
текущая
точка
(
ϕ
, r) опишет половину кривой, расположенную выше полярной оси.
Площадь плоской фигуры в полярных координатах вычисляется по формуле [1].
∫∫
=
Д
rdrdS
ϕ
, следовательно
()
.2cos
2
2sin
2
22
22
2
0
2
2
0
2sin
0
2
0
2
0
2
2sin
0
2
едa
a
da
r
drdrdS
a
a
=
−
====
∫∫ ∫ ∫
π
π
ϕ
ππ
ϕ
ϕϕϕϕϕ
Задача 6.
Вычислить с помощью тройного интеграла объем тела, ограниченного
поверхностями
.9,3,0
22
=+=+= yxzyz
Решение.
Сделаем чертеж.
Цилиндр
9
22
=+ yx
снизу ограничен плоскостью z = 0, а сверху плоскостью
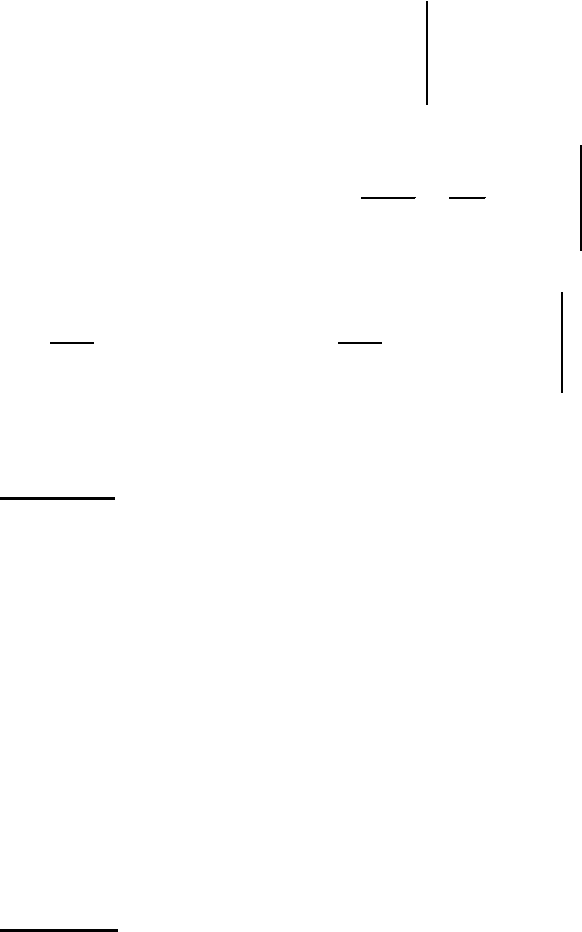
106
z = 3 - y и проецируется в круг x
2
+ y
2
≤
9 плоскости ХОY.
Поскольку область
Д – круг, то при вычислении объема данного тела используем
цилиндрические координаты [3], при этом
.3,99;sin33
222
==⇒=+−=−= rryxryZ
ϕ
[
]
{
}
∫∫∫ ∫∫∫
====
)()(
2
vv
dzrdrddxdydzV
ϕ
∫∫∫∫∫
==
−
−
π
ϕ
ϕ
π
ϕϕ
2
0
sin3
0
3
0
sin3
0
3
0
2
0
r
r
rdrzddzrdrd
∫∫∫
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−
ππ
ϕϕϕϕ
2
0
3
0
32
3
0
2
0
sin
32
3
)sin3( d
rr
drrrd
()
.27cos9
2
27
sin9
2
27
3
2
0
2
0
eдd
πϕϕϕϕ
π
π
=
⎟
⎠
⎞
⎜
⎝
⎛
−=
⎟
⎠
⎞
⎜
⎝
⎛
−
∫
Задача 7.
Вычислить криволинейный интеграл
∫
+−
L
ydyxdxxy
2
)1(
от точки А(1; 0) до точки В(0; 2):
а) по прямой
;22 =+ yx
б) по дуге параболы
;44
2
=+ yx
в) по дуге эллипса
.sin2,cos tytx
=
=
Решение.
а) Данный криволинейный интеграл представляет собой криволинейный интеграл
по координатам [3].
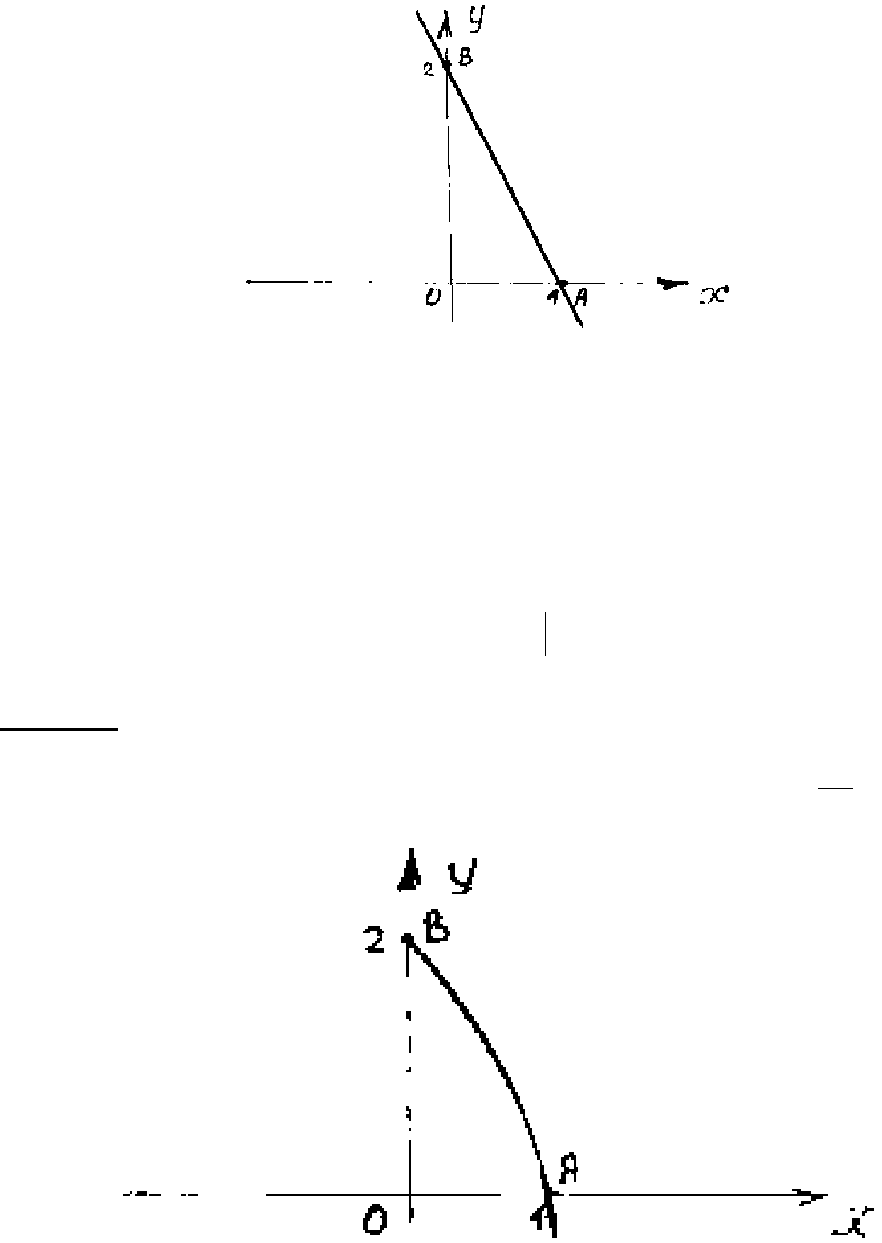
107
Линия интегрирования – прямая
,22
=
+
yx
откуда
.22 xy
−
=
,2dxdy −=
подставив
)(xfy =
и
dy
, преобразуем криволинейный интеграл в
определенный интеграл с переменной
х:
()
[]
=−−+−−=+−
∫∫
)2)(22(122)1(
22
dxxxdxxxydyxdxxy
B
A
X
XL
.1)2()1264(
0
1
234
0
1
23
=−+−=−+−
∫
xxxxdxxxx
Решение.
б) Здесь линия интегрирования дуга параболы
.
4
144
2
2
y
xyx −=⇒=+
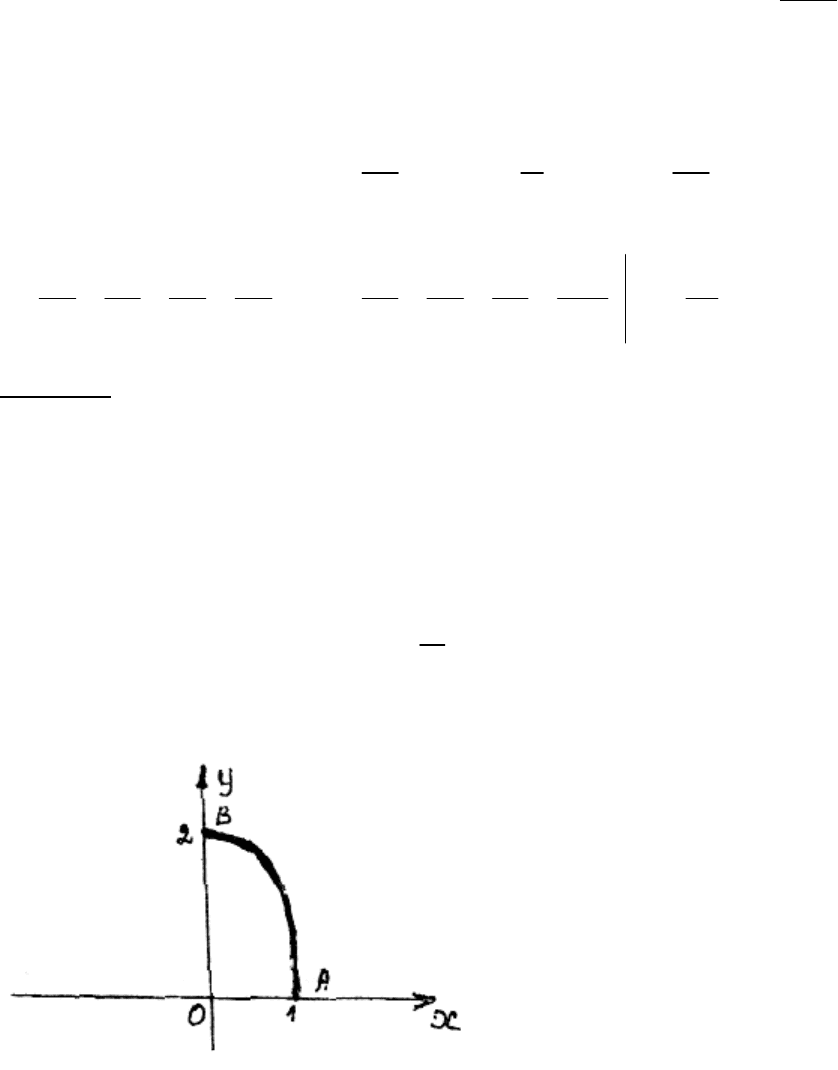
108
),( yx
ϕ
=
следовательно переменной будет
y
, найдем
,
2
ydy
dx
−=
подставив
х и dx в интеграл, вычислим:
∫∫
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+
⎟
⎠
⎞
⎜
⎝
⎛
−
⎥
⎦
⎤
⎢
⎣
⎡
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=+−
B
A
y
yL
ydy
y
dy
y
y
y
ydyxdxxy
4
1
2
1
4
1)1(
22
2
.
15
7
1
4
3
616402
3
248
2
0
2345
2
0
234
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+−−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+−−
∫
yyyy
dy
yyyy
Решение.
в) Линия интегрирования – дуга эллипса:
.sin2,cos tytx
=
=
Преобразуем
данный интеграл в определенный с переменной
t
и вычислим его:
;cos2sin2;sincos tdtdytytdtdxtx
=
=−==
.
2
)2;0(,0)0;1(
π
=⇒=⇒
BA
tBtA
∫∫
+−−=+−
L
t
t
B
A
tdtttydyxdxxy )sin)(1sin2(cos)1(
2
109
∫
=−+=⋅⋅+
2
0
232
)cossin2sinsincos4(cos2sin2cos
π
dtttttdtttdttt
∫∫∫
=−+−=
2
0
2
2
0
2
0
3
)(sinsin2sin)(coscos4
πππ
ttdtdtttd
.
3
4
)sin
3
2
cos(
2
0
34
=−−−=
π
tttsco
Задача 8.
Вычислить криволинейный интеграл
∫
+
L
xdyxdxy sincos
вдоль границы треугольника
АВС, обходя ее против хода часовой стрелки, если
А(-1; 0), В(0; 2), С(2; 0). Сделать чертеж.
Решение.
Сделаем чертеж.
Здесь линия интегрирования замкнутая, область внутри треугольника –
односвязная.
Подынтегральное выражение есть полный дифференциал функции двух
переменных, так как выполняется условие
xy
QP
′
=
′
[7], где
0
B
A C
y
X

110
x
x
Q
x
y
P
xyxQ
xyyxP
cos
cos
,sin),(
,cos),(
=
∂
∂
=
∂
∂
=
=
вследствие этого данный криволинейный интеграл, взятый по периметру данного
треугольника, равен нулю:
.0sincos =+
∫
L
xdyxdxy
Задача 9.
Дана функция
izzzfw +−==
2
)(
, проверить ее на аналитичность, если
функция аналитическая, то вычислить ее производную в точке
.
0
iz =
Решение.
Представим
)(zfw =
в виде
).,(),( yxiyxuw
+
=
Для этого подставим в
)(zfw =
iyxz
+
=
, где
1
2
−=i
[3].
=++−+== iiyxiyxzfw )()()(
2
=+−−−+= iiyxyxyix
22
2
),12()(
22
+−+−−= yxyiyxx
отсюда
,),(
22
yxxyxu −−=
.12
+
−
= yxyv
Если функция
)(zfw =
- аналитическая, то выполняются условия Коши-Римана:
,
y
v
x
u
∂
∂
=
∂
∂
.
x
v
y
u
∂
∂
−=
∂
∂
Найдем
