Crank J. Free and Moving Boundary Problems
Подождите немного. Документ загружается.


92
Free-boundary problems: formulation
On
the
bottom
boundary, Py(x,
0,
t) =
-1,
and finally the initial conditions
are
f(x,
0) = !o(x), and, for
v>O,
p(x,
y,
0) = Po(x, y).
The
problem is
to
find a pair (t, p) satisfying
the
above relationships where Yl(t), yz{t) fo(x),
Po(x, y) are given functions.
The
Baiocchi-type variable
w(x,
y,
t) = r p(x, y +
t-T,
T)
dT
is introduced, where p = p in
nand
p = 0 in D -
n,
where D is the
extended domain 0
< x <
a,
0 < y <
Y3'
The
existence, uniqueness, and
regularity
of
the solution of
an
appropriate variational inequality for w
follow from the theoretical papers referred to above.
Then
a priori
estimates and a convergence theorem are established for a finite-element
approximate problem of implicit type
but
an
explicit approximation could
be
introduced equally well.
The
final algorithm involves
the
iterative
solution of a non-linear set of equations for
Wij
when the mesh point (i,
j)
lies in
the
domain D and a simpler set of equations for points (i,
j)
on
the
bottom boundary.
The
first case is equivalent to a minimum problem in
One
variable and can
be
solved directly. Values finally adopted at
the
new
time level incorporate a relaxation parameter
of
1.7, though this is
not
known
to
be
optimum. Solutions are shown graphically for four different
situations involving rapid raising
or
lowering
of
reservoir heights from
an
initial steady-state position of the free boundary. A fifth problem starts
from a non-equilibrium free-boundary position specified as
fo(x) = 1
+0.3
sin
2'lTX
with Yl(t) = yz{t) = 0, t
~o.
The extension of the Baiocchi approach to time-dependent problems in
dams
of
general shape presents difficult quasi-variational problems.
Gilardi (1979, 1980) therefore adapted the formulation of
Alt
(1977,
1979, 1980a,b) given in §8.6 and
of
Brezis
et
al.
(1978) outlined in §2.11.
He
arrived
at
the following formulation of the problem: find a pair of
functions
(p,
x)
satisfying
p~O,
0.:;; x.:;;
1,
p(l-x)=O
in
n,
p = G
on
!,O,
G bounded and
~O
on
n,
X(O)
=
Xo
in
D,
L [Vp .
Vv+
X(vy-vt)]dx':;;O,
for any smooth v such
that
v(O) =
v(T)
=
0',
v
~
0
on
!'O.
This variational inequality reduces to
that
of Brezis
et
al. (1978) in
§2.11 when
V
t
= 0 and where v and X
take
the
places of , and
g.
In
the

Lubrication cavitation
in
a journal
bearing
93
time-dependent problem the space-time domain .0 stands
on
the area
domain
D of
the
dam
and extends over 0 < t < T in time, aD the
boundary of D comprises two parts
r ° and r 1> and I
o
,
II
are the
corresponding parts of the boundary surface of .0.
The
function
XO
specifies
the
initial wet
or
partially saturated region.
The
condition
p;;:.
0
indicates saturated
flow
in regions where p > 0
but
elsewhere unsaturated
flow
is allowed.
An
existence theorem for this evolution problem
is
proved
in
Gilardi (1979).
Visintin
(1980a,b) extended his formulation of the stationary problem
(Visintin 1979)
to
the time-dependent problem with reference to the Fig.
2.17 by introducing a new system of coordinates
(~,
'lJ,
'1")
corresponding to
a rotation
of
,"/4 in the (y, t) plane, i.e.
(
~\
=,(:)
= ( (y + :)/.)2 ) .
;}
t
(-y+t)/.)2
The
final variational inequality involved two unknown functions z+ and
z-
satisfying appropriate boundary conditions and Visintin proved an
existence theorem.
He
claimed
that
possible generalizations include
three-dimensional
flow,
a vertical sheetpile, and a capillary fringe.
The
non-stationary
flow
of a compressible fluid through a simple
rectangular porous dam, with fluid again moving through the base at a
rate
.f(x, t), was studied by Torelli (1977b).
He
used the Baiocchi trans-
formation
w(x,
y,
t) = r v
(x,
t+
y -
'1",
'1")
d'l",
where V is
the
extended form of
the
pressure over a fixed space-time
domain, to obtain theoretical results based on a variational ineqUality.
Rasmussen and Salhani (1981) described three different numerical
methods for more general unsteady, two-dimensional porous flow with a
free surface. They used a Rayleigh-Ritz expansion, a Kantorovitch ex-
pansion, and a coordinate transformation.
2.13.
Lubrication cavitation
in
a journal
bearing
This phenomenon which has been of practical and theoretical interest
to engineers for almost a century presents a classical elliptic free-
boundary problem (Pinkus and Sternlich 1961).
It
is
of historic interest
to
mathematicians in
that
Christopherson (1941) introduced for the first
time
the
idea
that
the
differential equation must be solved subject
to
an
inequality constraint
that
the
solution
be
non-negative.
In
fact,
he
used
94
Free-boundary problems: formulation
essentially what is now known
as
the
Cryer algorithm, with relaxation
instead
of
SOR, and
in
spirit, though
not
explicitly, formulated a linear
complementarity problem.
SOR
was first used by Gnanados and Osborne
(1964). Cryer (1971b) gave a mathematical analysis of Christopherson's
approach.
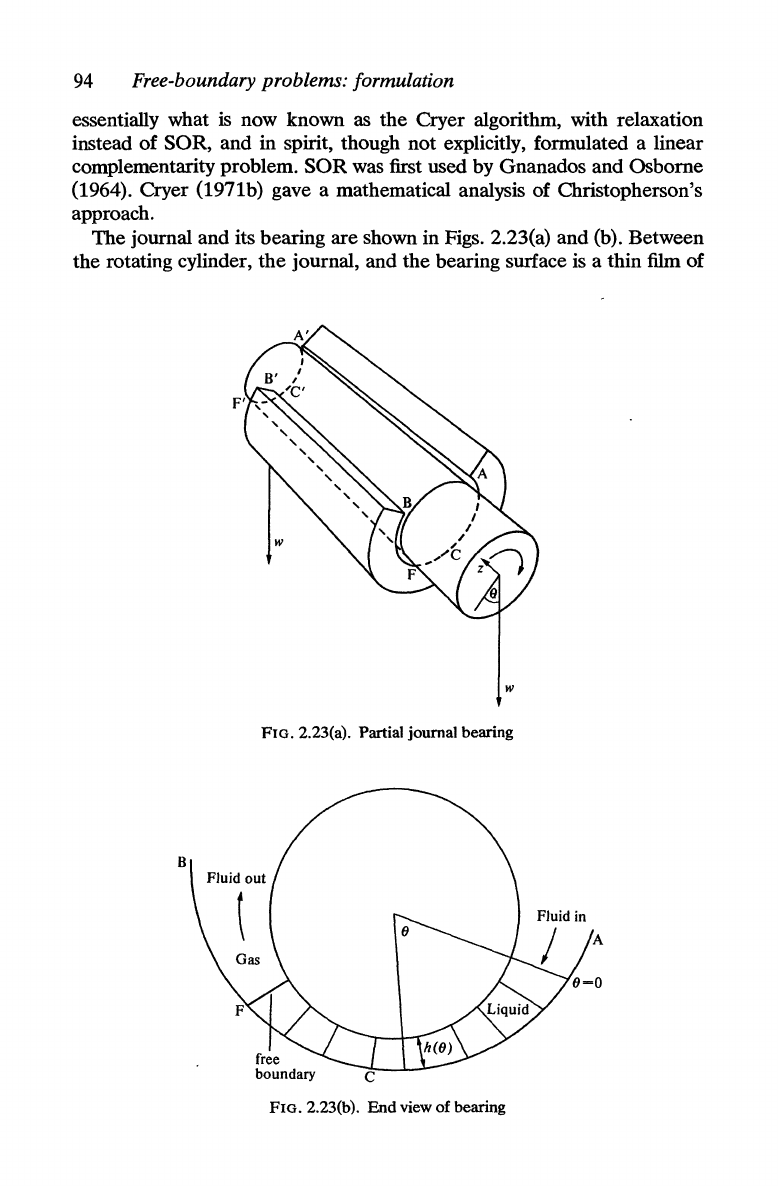
The
journal and its bearing are shown in Figs. 2.23(a) and (b). Between
the
rotating cylinder,
the
journal, and
the
bearing surface is a thin
film
of
w
FIG.2.23(a). Partial journal bearing
B
FIG. 2.23(b).
End
view
of
bearing

Lubrication cavitation
in
a journal bearing
95
lubricating fluid which is fed in along
AA'
(Fig.
2.23(a)) and
flows
out
through BB' and the ends ACB and
A'CB'.
H the width of the fluid
film
decreases between A and C and then increases
to
B, the pressure can
be
expected to increase between A and C and to decrease between C and B
(Fig. 2.23(b)). Along
AA',
BB', ACB, and
A'CB'
the
lubricant is in
contact with the atmosphere and the boundary condition there
is
p = 0,
if
pressure is normalized to zero atmospheric pressure. The lubricant occurs
in both liquid and vapour phases and the free boundary is the interface
FF' between liquid and vapour.
It
is
assumed that vaporization occurs at
zero pressure so that the inequality
p;;:.
0
is
satisfied everywhere.
Where p
> 0
the
liquid phase exists and the flow is determined by
Reynolds's equation in two dimensions
if, for a thin
film,
the
pressure
is
assumed not to vary across the gap. Then the equation is to
be
solved in
the
region
AA'FF
(Fig. 2.24), where the x-axis lies along
the
length of
the
cylindrical journal, 6
is
the
angular distance along
the
film,
and h(6) is
the
film thickness, a known function. The liquid region
is
denoted by n+,
the gaseous region by
00,
and the whole rectangle AA'B'B by
n.
The
problem is defined by the following equations and Fig. 2.24:
Lp=V·(h
3
Vp)-dh/d6=0
inn+>
(2.
157a)
p = 0 in
00,
p = 0
on
the boundary of
n,
(2.157b)
p=ap/an=O
on
FF,
6=s(x),
(2. 157c)
where
6=s(x)
is the free surface
to
be
determined together with p(6,x).
The
cavitation conditions (2.157c) ensure non-negative pressures. The
conditions dh/d6
< 0, 6 A < 6 < 6
c
and dh/d6 > 0, 6
c
< 6 < 6
B
ensure that
the
free boundary lies above 6 = 6
c
(Elliott 1976).
o
B~------------------~B'
p-o
Vapour
Liquid
p>o
A~------------------~A7,---X
FIG. 2.24. Journal bearing: solution domain

96
Free-boundary problems: formulation
We
note
that
this problem is already
in
variational form in
the
original
variable
p(O,
x)
because of
the
conditions (2.157c).
In
fact,
-V·
(h
3
Vp)+dhldO;;::'0,
p;;::'O
inn,
p{-V'
(h
3
Vp)+dhldO}=0,
(2.158)
and finally
J J h
3
Vp .
V(v-p)
dx
dO;;::'
- J
J(dhldO)(V-P)
dx
dO
(2.159)
o 0
for all v
;;::.
0 in
n,
square integrable
together
with its first derivatives,
and
v = 0
on
the
boundary
of
n.
Figure
2.24
refers
to
a bearing of finite length, - L ~ x
~
L say.
If
L is
very large
so
that
the
pressure variation
in
the
axial direction is small
the
problem is
treated
as
one
dimensional with p =
p(
0) and describes
an
infinite journal bearing. Cryer
proved
the
existence of a unique solution
for this case
and
developed
the
theory
of
his
SOR
algorithm
to
find
numerical solutions of a discretized formulation.
Meyer
(1978d) used his
method
of
lines (see §4.4)
to
solve
the
two-dimensional problem
and
showed
that
his solution converged
to
that
of
the
variational inequality (2.159).
He
also stated
that
the
method
of
lines could
be
applied with little change
to
more
realistic technical
problems.
Some unsolved free-boundary problems from
the
theory
of
lubrication,
including
the
conditions
on
a cavitation free boundary,
are
discussed
by
Capriz
and
Cimatti (1980).
2.14. A more general look at the Baiocchi transformation
Several examples
of
the
use
of
the
Baiocchi transformation and
method
have
been
described in this chapter.
The
aim in this section is
to
present
a
more
general statement
of
free
boundary
problems in terms
of
variational
inequalities.
The
individual physical situations emerge as special cases.
In
particular, two questions
are
examined systematically: first
what
deter-
mines
the
need
for a Baiocchi transformation
in
some problems
but
not
in
others; second,
in
what
direction, i.e. with reference
to
what
independent
variable, should
the
integration in
the
Baiocchi transformation
be
per-
formed?
What
follows
is
based
on
an
elucidation by Baiocchi himself
(1980b).
A typical free-boundary
problem
can
be
stated
as follows, without any
reference
to
a particular physical situation for
the
moment.
We
denote
the
Laplace
operator
for n independent variables
by
VZu
=
Lf=l
a
2
ulaxr
in
a fixed
open
domain
D.
Given f
and
tfJ,
two
real, smooth functions
on
fj,

A more general look
at
the Baiocchi transformation 97
i.e.
the
domain D together with its boundary
aD,
we wish
to
find a pair
{n,
u}, where n is
an
open
sub-domain
of
D with boundary
an
also
included in
D,
u
is
a function defined
in
.n,
and
both
nand
u
are
to
be
smooth.
The
conditions
to
be
satisfied are:
-V
2
u=f
in
n,
(2.160)
u=I/I
on
annD,
(2.161)
grad u = grad
1/1
on
annD,
(2.162)
u=O
on
an
n
aD.
(2.163)
The
'fixed'
part
of
the
boundary
of
n is also
part
of
aD
and written as
annaD
in (2.163)
and
other
types
of
this condition
are
admissible, e.g. a
Neumann derivative condition.
The
'free
boundary' is denoted by
an
n D
and
(2.161), (2.162)
are
the
two conditions needed because this boundary
is unknown.
A
more
general free-boundary problem arises
if
the
Laplace
operator
is
replaced by
an
operator
L so
that
(2.160) becomes
n n
Lu
= L
-«(J;jUx.}".
+ L
biUx.
+cu =
finn,
(2.164)
iJ=l
i=1
and
instead
of
(2.162) we
take
1:
(J;j(u
-
1/1)",
+
1:
gj(u -
1/1)",
=0
on
annD,
(2.165)
i.j=l
j=1
for a prescribed
g=(gj(x)).
Here
Ux.
=
au/aX;
etc., x denotes
the
vector
x =
(Xl,
X
2
,
•••
,
x;,
...
,x,,),
and
g = (gl,
g2,
...
,
&,
...
,g,.).
For
the
Lap-
lace
operator
(J;j
= 1, i =
j;
(J;j
= 0,
if
j;
and
with g
=0,
(2.165) is equival-
ent
to
(2.162).
By
(2.161), u -
1/1
= 0
on
the
free boundary and therefore
grad(u -
1/1)
is parallel
to
Va,
the
unit
outward
no~al
to
an.
Thus, (2.165)
can
be
written
in
the
form
[a·
grad(u-
1/1)-
g].
Va
=0
on
annD,
(2.166)
where
a'
grad(u-I/I)
is
the
vector with components
:Lj=l
(J;j(u-I/I)", with
i =
1,
...•
n.
If
now we denote
by
K a set of admissible functions
v,
which
are
square summable together with their first derivatives, and v = 0
on
aD,
v
;;?;
1/1
in
D,
we can write
K
={v
E
Hh(D):
v
;;?;I/I},
where
Hh(D)
is
the
usual Sobolev space
of
functions which are zero
on
aD.
Then
the
free boundary problem becomes
to
find u E K such that
a(u,
u-v).:;;;(u-v)
for all
VEK
(2.167)

9H
Frel'-hol/III/ar.\'
/)1'11"'1'111.1':
/iJl'll/u/atiol/
where
a(u,
v)
f f grad u . grad v
dx
dy,
(u-V)=
fff(U-V)dxdY.
n
The
proof
of
(2.167)
is
as for (2.36) outlined in §2.2.4.
Several physical problems have
been
formulated in this way in
the
preceeding sections.
We
rely
on
the
original theorem by Stampacchia
(1964) for existence
and
uniqueness results
on
u.
In
order
to
show
that
with U a solution
of
(2.167)
and
0 defined
to
be
the
sub-domain of D for
which U >
"',
the
pair
{O,
u}
solves
the
problem
of
equations (2.160-3),
we need
to
investigate further
the
smoothness of
u.
We
appeal
to
the
theoretical work
of
Lewy and Stampacchia (1969) for
the
important result
that
the
solution
of
(2.167) implies u
is
in C1(D), i.e. has continuous first
derivatives in
D.
We
require also
that
'" is in C1(D).
If
we
take
u
to
be
the
restriction
of
u
to
n,
then
(2.161) holds by
the
definition
of
0;
(2.163) is
true
because u E
Hb(D);
(2.162) holds because
u - '" is a C
1
function which
is
non-negative,
and
so grad(u - "') = 0
where u - '" = 0, i.e.
on
the
free boundary. Finally, we refer, for example,
to
Baiocchi et
al.
(1973a) for
the
proof
that
the
solution
pair
(0,
u)
of
(2.167) provides a
weak
solution
of
the
original problem (2.160-3).
We
noted
that
the
conditions (2_161)
and
(2_162), which lead
to
the
continuous first derivatives of u
on
the
free boundary
that
are essential
for a variational formulation, correspond
to
g
==
0 in
the
generalized free
boundary condition (2.166). This
point
was
noted
by Levy
and
Stampac-
chia (1969).
The
implication is
that
problems in which g
is
not
zero
cannot
be
solved directly through a variational inequality.
In
general
we
must expect limited continuity
of
u across
the
free boundary (Brezis,
1972a,b). Thus,
if
we define
L2(0)
to
be
the
space
of
square integrable
functions
in
0
the
solution
of
(2.167) belongs
to
H2(0)
provided f
belongs
to
L 2(0).
We
now briefly categorize some
of
the
free boundary problems consi-
dered
earlier
in
this chapter
and
some
of
the
moving boundary problems
formulated in
Chapter
1 as special cases
of
the
general problem defined
by (2.164)
and
(2.166). Especially, we see whether they
are
immediately
amenable
to
variational solution
and
if
not
what form
the
Baiocchi
variable should take.
(i)
Journal bearing.
The
equations (2.157a-c) describing
the
cavitation
problem in a journal bearing (§2.13)
are
in
the
form
of
(2.164)
and
(2.166) with '" = 0
and
g = 0
and
it
was directly expressible as
the
variational inequality (2.159).
(ii) Oxygen diffusion. Similarly,
the
diffusion
of
oxygen in absorbing
tissue, formulated
in
equations (1.57-60) corresponds
to
L = O/at-iP/ax
2
,

A more general look at the Baiocchi transformation
99
f=-l,
1/1=0,
and from (1.58),
g=O,
and is fonnulated directly in the
variational
fonn
of (6.141).
(iii) Simple rectangular dam. With suitable change of nomenclature, e.g.
</>
replaced
by
u,
y
by
Xl>
and x by
~,
equations (2.7) and (2.9) in §2.2
are like (2.160) with
f = 0,
1/1
=
x,
and
the
second condition in (2.9) on
the
free boundary can
be
put
in
the
form of (2.166) with
g1
=-1,
&;
=0
for
i
=f
1.
The
Baiocchi variable (2.20) therefore had
to
be
defined in order
to
introduce
the
continuity necessary for
the
variational
fonn
(2.36).
The
direction of integration in (2.20) is
Xl>
e.g.
gl>
and this was found
necessary and useful in
other
steady dam problems fonnulated in §2.3.
Difficulties which still arose in some cases were
due
to
the
conditions on
the
fixed boundaries.
(iv)
Evolution dam
problem.
The
dam is denoted
by
Do
in
two
or
three
space dimensions (m = 2
or
3) for
the
non-steady dam problem of
§2.12.4, and
D denotes
the
space-time domain
on
the
base Do and
extending in time t over
the
range 0".;
t".;
T.
If
the
coordinate
x..
in
(2.164), for example, is written
x..
= t and n = m + 1,
the
evolution dam'
problem still has the
fonn
of (2.160) and (2.161) with
f=O,
I/I=xbthe
vertical component,
but
V
2
involves
the
space variables only.
The
only t
derivative appears in
the
free boundary condition
Ut
=
grad u . grad( u -
Xl)
and grad involves only space variables. This condi-
tion is like (2.166) with
g1
=-1,
gj
=0
for
l<i<n,
and
gn
=-1.
Torelli
(1977a) used
the
variable
t+Y-T
for
the
integration in
the
Baiocchi
variable (see §2.12.4).
(v)
One-phase Stefan problem. By retaining
the
nomenclature of the
previous problem
(iv)
but
with Do denoting the ice-water region and D
its extension
to
the
space-time domain for 0".;
t".;
T,
the
melting ice
problem
d~ribed
in one dimension, for example, in §1.2.1 is (2.161),
(2.164), and (2.166) with
f=
1/1
=0,
L =
a/Ot-~,
and O(x,
t)
is
the
water
region.
In
§1.3.9
the
usual condition (1.56b)
on
the
melting boundary is
expressed in
the
fonn
(1.56k).
For
a one-phase problem in
the
present
nomenclature this becomes (grad
U)2
=
93uc,
with
91
a
heat
parameter,
which has
the
fonn
(2.166) with
&;
=0
for
i<n,
gn
=-91.
This indicates
immediately
the
need for
Duvaut
(1973) transfonnation (6.159) where
the
integration is in
the
t-direction.
To
summarize,
the
direction of integration in
the
examples (i)-(v)
was
always in
the
direction of
g,
with no integration needed
if
g =
O.
Baiocchi
(1976) established this
as
a general result for free-boundary problems; a
similar investigation for Stefan-like, moving boundary problems was
carried
out
by Gastaldi (1979).
In
tenns
of p, a continuous extension of u
defined by
p =
u-I/I
in
n,
p=O
inD-n,
(2.168)

100
Free-boundary problems: formulation
the
general problem defined by (2.164), (2.161), (2.166) was expressed by
Stampacchia (1964)
as
Lp
= Xo(J - Li{!) - g . grad
Xo,
(2.169)
where
XO
is
the
characteristic function of
fi
in D, i.e.
XO
= 1 in
fi
and
Xo=O
in
D-fi.
The
relation (2.169) follows from (2.164), (2.166),
(2.168) and confirms
that
a Baiocchi integration along
the
direction of g
can remove the difficult term grad
Xo.
Elliott and Ockendon (1982) comment
on
the
difficulties of generaliz-
ing
the
above derivation of variational inequalities. They also illustrate
the
possible existence of more than
one
conservation formulation for a
particular problem, e.g.
the
rectangular
dam
problem. Only conservation
laws with appropriate discontinuities in
the
dependent variables can
be
diagnosed
as
amenable
to
weak and variational formulations.
In
general
there are no
firm rules for guidance.
2.15. Connections between
certain
free-bonndary problems
Rogers (1980) examined systematically
the
connections between
the
single-phase Stefan problem,
the
problems of oxygen diffusion and elec-
trochemical machining, and
the
time-dependent dam problem which have
been formulated earlier in this chapter and in
Chapter
1. Rogers
pro-
posed truncation algorithms for
the
numerical solution of these problems
which have close
affinity with linear complementarity algorithms as noted,
for example, in §6.4.4. Rogers's findings on
the
connection between the
evolution dam problem and that of electrochemical machining reflect
the
use of Rele-Shaw flow as an analogy for two-dimensional porous flow
on
the one
hand
(see §2.12.1) and its similarity of mathematical formulation
to
that
of electrochemical machining
on
the
other
(see §2.12.3).

3. Analytical solutions
3.1.
Exact
simllarity solutions
VERY
few analytical solutions are available
in
closed form. They are
mainly for
the
one-dimensional cases
of
an infinite
or
semi-infinite region
with simple initial
and
boundary conditions and constant thermal proper-
ties. These exact solutions usually take
the
form
of
functions
of
the
single
variable
xlt~
and
are
known as similarity solutions. Corresponding solu-
tions which
are
functions
of
rlt~
only
are
available in cylindrical and
spherical coordinates. Some similarity solutions
have
been
obtained for
combined
heat
and
mass transfer
in
a semi-infinite region. A good
collection
of
similarity solutions and references
is
to
be
found in Carslaw
and
Jaeger (1959).
3.2. Neumann's solution; geners-lizations; volnme changes
A similarity solution which predates
the
work
of
Stefan himself was
apparently presented in lectures given by Franz Neumann in
the
1860s
(Riemann-Weber 1912).
It
refers
to
a semi-infinite region, x
>0,
initially
occupied by a liquid
at
a constant temperature greater
than
the
melting
point
and
with
the
surface, x = 0, subsequently maintained
at
a constant
temperature
below
that
of
melting. Neumann's solution for this problem
is reproduced
by
Carslaw
and
Jaeger (1959,
Chapter
IX) together with
Stefan's results (1891) for
the
special case in which
the
liquid is initially at
its melting point.
In
fact, this latter result had
been
obtained previously
by
Lame and
Qapeyron
(1831).
The
corresponding problem
of
melting a
solid in
the
region
x>
0, initially
at
a temperature below
the
melting
point, is presented
here
to
illustrate Neumann's method.
It
is convenient
to
refer
to
ice
and
water
purely for descriptive reasons and
to
adopt
the
nomenclature
of
§ 1.2.2, except
that
x,
t,
k etc. will
be
used for conveni-
ence even when physical variables with appropriate dimensions are sig-
nified.
