Crank J. Free and Moving Boundary Problems
Подождите немного. Документ загружается.


82
Free-boundary problems: formulation
between two vertical plates, separated by a small distance
2a
so that
the
flow
can
be
considered two-dimensional. With reference
to
axes indicated
in Fig. 2.18, where
y is vertically upwards, u
and
v denote mean velocity
components between
the
plates.
It
follows easily from
the
general
equa-
tions of flow that (see Safiman and Taylor 1958)
-a
2
ap
u=---
121£
ax'
-a
2
(a
p
)
v
=
121£
ay + pg ,
corresponding
to
a velocity potential given by
a
2
<I>
=
121£
(p + pgy).
(2.136)
(2.137)
Comparison with (2.2) shows
the
direct analogy with flow in a porous
medium of permeability
a
2
/12, remembering
that
u and v are mean
velocities in
the
Rele-Shaw flow.
It
remains
to
examine
the
conditions
on
an interface between two
fluids, for example when fluid 1 is being pushed out completely by fluid 2.
The
mean velocity
U1
in fluid 1, ahead of
the
interface, is
-a
2
U1
=
121£1
grad(p +
P1GY)
= grad
<1>10
and in fluid 2, behind
the
interface,
the
mean velocity is
-a
2
U2
=
121£2
grad(p +
P2GY)
= grad
<1>2.
If
a is small,
the
width of
the
projection of
the
meniscus
on
to
the
plates
is small,
and
the
expressions for u can
be
assumed
to
hold right
up
to
the
interface, which can
be
regarded as a sharp line.
It
follows
that
the
components of
U1
and
U2
normal
to
the
interface are continuous across it.
Furthermore,
if
surface tension effects are negligible; the pressure p is
constant across
the
interface. Thus the motion of
the
two fluids repro-
duces that of
the
interface between two fluids of viscosities
1£1
and
1£2
in a
porous medium with permeability
a
2
/12.
2.12.2. Hele-Shaw injection
Richardson (1972) considered
the
injection of fluid into an infinite cell
by a point source placed in
the
centre of
an
initially fluid blob which
subsequently expands. His practical interest was in injection moulding.
Elliott
and
Janovsky (1979) formulated
the
problem of a finite injection
source in a horizontal finite cell in terms of an elliptic variational
inequality.
The
time-dependent nature of
the
problem appears only in

Degenerate free-boundary problems
83
FIG. 2.19. Injection into horizontal cell
the
condition
on
the
moving boundary, which is
the
surface of
the
expanding fluid blob.
With
reference
to
Fig. 2.19,
the
fluid initially occupies
the
domain Do
lying between
the
two curves r 0
and
r
I
and
more
fluid
is
subsequently
injected
at
a constant
rate
Q>O
through
the
surface
rio
The
region
between
r
I
and
the
outer
wall
of
the
cell r
is
denoted
by
D.
The
moving
boundary
is
r"
for
time
t > 0;
at
t = 0, r
t
==
f
0;
D
t
denotes
the
domain
between
r
I
and
r
t
•
Applying
the
general discussion
of
§2.12.1
to
the
horizontal cell we
can
write
v=-Vp
where
v = (v
x
,
v
y
)
is
the
fluid velocity
and
p
is
a modified pressure defined
by
a
2
/(12/L)P,
where
P(x, y)
is
the
true
pressure.
In
the
incompressible
fluid
~p=O.
(2.138)
The
velocity
of
the
moving boundary,
r"
is
taken
to
be
Vn
in
the
direction
of
the
outward
pointing normal n,
and
the
pressure
on
r
t
is assumed
to
be
always zero.
When
the
fluid reaches
the
cell wall
the
flow is assumed
tangential
and
the
normal
derivative
of
pressure,
Pm
vanishes.
It
is
convenient
to
define ft,
t>O,
by
r
t
=s(x,
t)=
t-t(x)=O,
(2.139)
with
x denoting
the
space coordinate vector
(Xl,
x:z),
such
that
at
time t
the
fluid occupies
the
part
of
D in which X satisfies
t(x)
<
t:
the
function
t(x)
is unknown a priori.
The
classical formulation
of
this
problem
is
p=O,Pn
=-v",
as
or
Vp·
Vs
=-
or
Vp·
Vt=-1
on
r"
at
Pn
= Q
on
rb
Pn
= 0
on
r,
t(x)
= 0 in Do.
(2. 140a)
(2. 140b)
(2. 140c)
(2. 140d)

84
Free-boundary problems: formulation
Following
Duvaut
(1973)
and
Elliott (1980) a new
dependent
variable
u(x, t) is introduced defined
by
u(x,
t)
= r p(x,
'1")
d'l"
in
D,
t>O. (2.141)
On
the
fixed
and
moving boundaries
Un
=0
onr,
Un
=Qt
onrJ,
u =
Un
= 0
on
r
t
•
(2.142)
Assuming
p
and
t(x)
to
be
smooth, it follows from (2.141)
by
using
(2.140b), (2.140a)
that
and
Vu =
It
Vp(x,
'1")
d'l"
in D
t
,
~(x)
t(x)<t<T,
v
2
u = 1 in D
t
,
V
2
u
=0
in Do,
t(X)<t<T,}
O<t<T,
(2.143)
(2.144)
where
t = T is
the
final time
at
which
the
cell is completely filled.
Thus
in
the
domain
D,
u(x, t) satisfies
the
inequalities
(-~u-f)-;;;.O,
u-;;;'O,
(-~u-f)u=O,
on
D,
(2.145)
since
u(x, t)=O in
D-D
t
and
where
f(x)=O
in Do
and
f(x)=-l
elsewhere.
The
elliptic variational inequality corresponding
to
(2.142)
and
(2.145)
is
J
Jvu.
V(v - u) dXl
dx
2
-;;;.
J Jf(V-u)
dx
1
dX2
+ L
Qt(v-u)
ds, (2.146)
D D '
where
the
functions u
and
v
together
with
their
first derivatives
are
square integrable in
D.
There
is
the
equivalent minimization
statement
J(u)~J(V),
(2.147)
where
J(v)
=~
J
JIVV\2
dXl
d~-
J
Jtv
dXl
dx
2
-
L
Qtv
ds.
D D I
The
most interesting feature
of
(2.146)
and
(2.147) is
that
time
tenters
only as a
parameter
in Qt
and
thus
the
free
boundary
r
t
may
be
found
at
any required time
t*
by
solving
one
elliptic free boundary problem with
Qt
= Qt*, without
the
need
to
determine
the
solution
at
times
prior
to
t*.
Mathematical properties
of
the
solutions
and
their existence, unique-
ness,
and
regularity were examined
by
Elliott
and
Janovsky (1979, 1981,
1983). They expressed (2.146), (2.147) as a discrete linear complementar-

Degenerate free-boundary problems
85
ity problem ansmg from a finite-element discretization and obtained
solutions
by
using
the
SOR
with projection algorithm described in
§8.5.1(i). They included an error analysis and presented solutions graphi-
cally for two problems:
(i) for an elliptic source inside a square container;
and
(ii)
for the injection
of
fluid into a mould lying between two
semicircles.
2.12.3. Electrochemical machining
As an alternative
to
mechanical machining, a piece of metal can
sometimes
be
shaped by using it as an anode in an electrolytic cell with an
appropriately shaped cathode. This is a moving boundary problem be-
cause
the
anode surface changes with time. A detailed account of the
physical and practical details of the process and its industrial uses are
given by McGeough (1974). Essentially, the anode is moved towards the
cathode,
or
vice versa, at a constant velocity
and
the
products of
the
erosion
of
the
anode
are
swept away by
the
electrolyte which is pumped
through
the
space between
the
electrodes. The cations combine with
the
electrolyte
to
form gases
and
so
the
cathode shape does not change.
Several authors have studied a quasi-steady mathematical model in
which the electrodes are assumed
to
be
equipotential surfaces,
and
the
electrolyte
to
be
homogeneous
and
isotropic with constant conductivity.
Hougaard (1977) gave references
to
pioneer papers
and
formulated two-
dimensional problems
on
the
complex-potential plane.
The
transformed
boundary condition& depend
on
the
cathode shape
and
may
be
so
complicated that classical analytical
or
semi-analytical methods
of
solu-
tion have
to
be
replaced by purely numerical methods. HougaI'd pre-
sented methods
and
solutions based
on
integral equations for a number of
cathode shapes. Two basic geometrical arrangements have been investi-
gated.
The
two-dimensional annular problem
of
shaping a cylindrical
anode by placing it inside a long cylindrical cathode has been treated by
Christiansen and Rasmussen (1976), who formulated the problem as an
integral equation
of
the first kind (see §8.7.1). Hansen
and
Holm (1980)
used an integral equation of
the
second kind. Meyer (1978e) applied his
method
of
lines (§4.4)
to
the
Poisson equation with electrochemical
machining as an example.
An
enthalpy-type formulation by Crowley
(1979) is described in §6.2.7(i).
Elliott (1980) formulated a variational inequality for this problem
and
drew attention
to
the
close analogy with the Hele-Shaw injection problem
discussed above in §2.12.2. This analogy can
be
anticipated from the
similarity between
the
generalized Fig. 2.20 for electrochemical machin-
ing
and
Fig. 2.19.
The
anode is
the
shrinking region
A(t)
with moving
boundary
r
t
and r 0 denotes
the
initial anode surface
at
t =
O.
The
region
inside
the
cathode surface C is denoted by D and the region occupied by

86
Free-boundary problems: formulation
c
FIG. 2.20. Annular electrochemical machining
the electrolyte
by
Db so that D includes
A(t)
and D
t
•
If
c/>(x,
y)
is
the
electric potential field,
the
mathematical problem is
to
find
c/>(x,
t) and
t(x)
such that
VZc/>
= 0 in D
t
,
S(t,x)=t-t(x)=O
on
rb
t(x)
= 0 in Do,
c/>
= 0 on
C,
q,
=
V(t)
on
r
t
Vc/>
•
VS
=
-L
as/at}
Vc/>
•
vt=
L.
(2. 148a)
(2. 148b)
(2. 148c)
(2. 148d)
(2. 148e)
Here
V(t)
is
the
potential difference between
the
electrodes
and
L
>0
is
a known constant of
the
system. This formulation is based on Faraday's
and Ohm's laws (McGeough and Rasmussen 1974).
Elliott (1980) formulated a variational inequality for this problem
following
the
arguments used in §2.12.2.
The
maximum principle for
Laplace's equation (2.148a) states that
O""c/>(x,
t)""
V(t).
For
each
t,
q,(x, t) is extended
to
all of D by q,(x, t) =
V(t)
in
A(t)
and
so
V(t)
-
c/>(x,
t);;:.:
0 in D.
The
Baiocchi variable u(x, t) in this case is given
by
U(x, t) = r
{V(T)-
q,(x, T)} dT in
D,
Corresponding
to
(2.145) we can deduce
that
-Vlu-f;;:':O,
u;;:.:O,
(-V
2
u-f)u=0
onD,
t>O.
(2.149)
(2.150)

Degenerate free-boundary problems
87
where f(x)==-L in
Ao
and f(x)
==0
in Do. Finally, using
the
conditions
(2.148d), (2.148e) we have
u(x,
t)
= r
V(r)
d'T
==
W(t)
on
C,
u =
u,.
= 0
on
r
t
•
(2.151)
Thus, as in the Rele-Shaw problem,
the
anode surface at any specified
time can
be
obtained by solving a single elliptic free boundary problem
and
t enters only through
the
boundary condition, u = W(t).
The
elliptic variational inequality follows easily since,
if
u(x, t) is a
classical solution of (2.150)
and
(2.151),
I
Ivu.
V(v-
u) dXl
dX2
= J
Ivu
.
V(v-u)
dXl dx
2
D
D,
= I I
-V2U(V-U)dXl~+1
u,.(v-u)ds
+r,
D,
= I I
f(
v - u) dXl
dx
2
~
I I
f(
v - u) dXl
dx
2
,
D,
D
i.e. for each t
~O,
u is
the
solution of
J
Ivu
. V(v - u) dXl
dX2~
I Jf(V- u) dXl
dX2,
(2.152)
D D
where u
and
v are, together with their first derivatives, square integrable
in
D,
v~O
in
D,
and
v = W(t)
on
C.
The
corresponding minimization
statement is
J(u).".J(v),
(2.153)
where
J(v)=~
J
IIvv
l2dx
l
d~-
I
ltv
dXl
dx
2
.
D D
Elliott (1980) proved some regularity results for u(t)
and
gave some
numerical results obtained by a finite-element approximation
to
(2.152)
with
error
estimates. His results for
one
problem are compared with those
of
other
authors in Table 8.25.
The
second geometric arrangement considered calls fo. the solution of
a two-dimensional planar problem between rectangular electrodes,
theoretically of infinite area.
The
quasi-steady-state model for this case
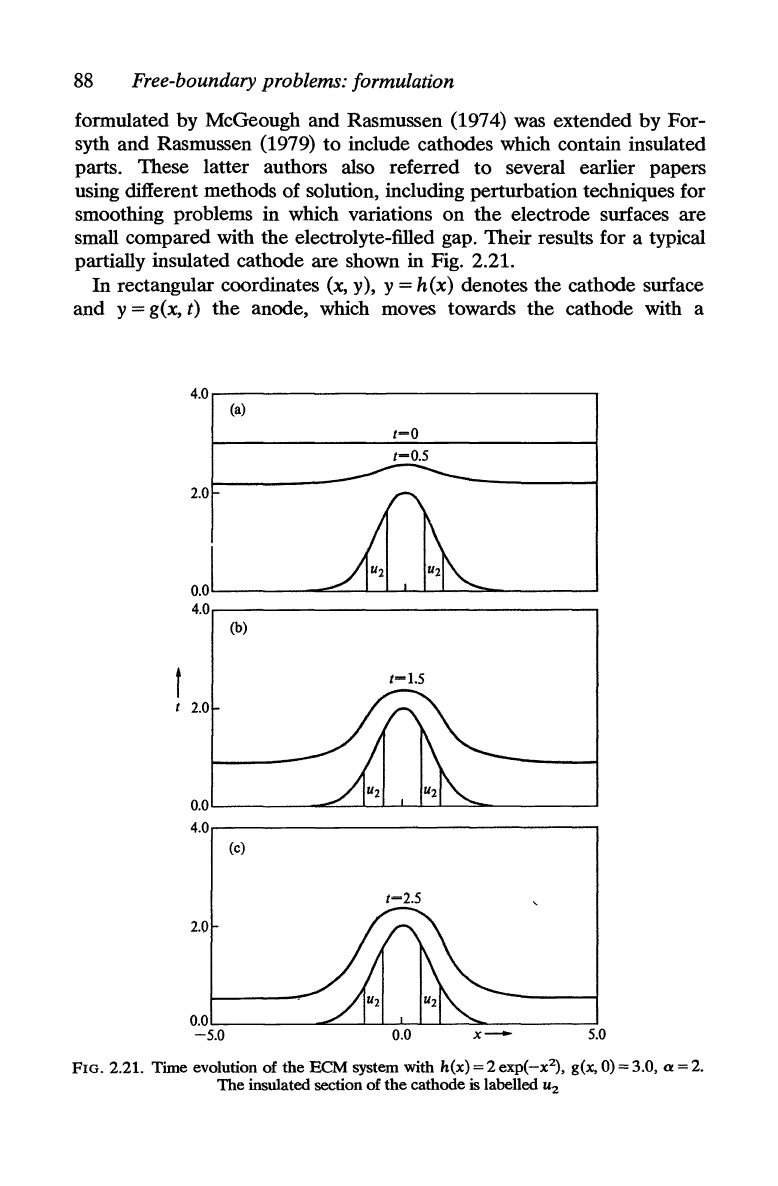
88
Free-boundary problems: formulation
formulated
by
McGeough
and
Rasmussen (1974) was extended
by
For-
syth
and
Rasmussen (1979)
to
include cathodes which contain insulated
parts.
These
latter authors also
referred
to
several earlier papers
using different methods
of
solution, including perturbation techniques for
smoothing problems in which variations
on
the
electrode surfaces
are
small compared with
the
electrolyte-filled gap.
Their
results for a typical
partially insulated cathode
are
shown in Fig.
2.2l.
In
rectangular coordinates (x, y), y =
hex)
denotes
the
cathode surface
and
y = g(x, t)
the
anode, which moves towards
the
cathode with a
4.0,....------------------,
(a)
1-0
1-0.5
2.0
O.OL-
____
=---L-L....I-.J..-L--=
____
--'
4.0.--------------------.
(b)
1=1.5
1
2.0
O.O'------""'---'--l---'-.L.......JL-..;::,..-------'
4.0,.-------------------,
(c)
1=2.5
2.0
O.O'--
____
""---'---'--'-.1........JL..-...=..
____
--:-'
-5.0
x-
5.0
FIG. 2.21. Time evolution of
the
ECM
system with
h(x)=2exp(-x2),
g(x,
0)=3.0,
a=2.
The
insulated section of
the
cathode
is
labelled u
2

Degenerate free-boundary problems
89
constant velocity a.
The
potential
cf>
is given by
VZcf>
=
(fcf>
+
(fcf>
= 0
ax
z
ayZ
,
(2.154)
cf>
= 0,
y
= h(x),
cf>
= 1, y = g(x, t).
If
there are insulated parts of
the
cathode, V
z
, and conducting parts,
Vi>
the
conditions in (2.154) become
y
= h(x). (2.155)
The
boundary condition
on
the moving anode is
ag=
acf»
_ ag
acf»
_ a =
Vg
.
Vcf>
- a,
at
ay g
ax ax
g
(2.155a)
where
acf>laY)g
denotes the value of
the
derivative
at
y = g(x, t), etc.
Forsyth
and
Rasmussen (1979) confined attention
to
functions h(x),
g(x, t) which approach straight lines of zero slope as x
~
±oe.
In
principle, the solution proceeds in small time steps and
at
each step
the
classical, fixed boundary-value problem defined by
VZcf>
= 0 and the
boundary conditions appropriate to
the
time is solved with the anode
treated
as a fixed surface.
The
condition (2.155a) is then used
to
deter-
mine a new anode surface which becomes the fixed boundary in the next
time step. Forsyth and Rasmussen (1979) used a variational method to
solve Laplace's equation in a transformed domain with straight bound-
aries by using the body-fitted curvilinear coordinates discussed in relation
to
Stefan problems in §5.2.
The
new feature is that
the
coordinate
transformation
is
applied directly
to
the
variational integral. These au-
thors presented numerical and graphical solutions for different cathode
shapes.
Later
Hansen (1983) was critical of the simple mathematical model
studied in these earlier papers because no account was taken of the flow
of
electrolyte between the electrodes.
He
generalized his integral equa-
tion method (Hansen 1980) (see §8.7.1) in order
to
deal with practically
realistic geometric shapes, and obtained numerical results which could
be
compared with experiments.
He
concluded that
at
the upstream
end
of
the
electrode gap the quasi-steady state model, with no allowance for
electrolyte flow, predicts the anode profile reasonably well.
In
the middle
and downstream regions, however,
the
predictions are
poor
because,
Hansen thought, the bubbles
of
gas, evolved
at
the cathode and swept
along in the electrolyte, form an insulating screen which reduces
the
local
current density. More details of the integral equation method in this
context are given in §8.7.
90 Free-boundary problems: formulation
2.12.4. Evolution
dam
problem
When a dam separates two reservoirs in which
the
water levels depend
on time the problem
is
a degenerate one. The velocity' potential
is
harmonic in
the
flow region but the free surface varies with time and
is
not a streamline.
The
condition
a4>/an
= 0 on the free surface
is
replaced
by
<f>t
- V
4>
• Vp =
O.
Unsteady
flow
of an incompressible fluid in a rectan-
gular dam (Fig. 2.22) was studied theoretically by Friedman and Torelli
(1977) and Torelli (1975,
1977a,b);
he
also allowed for fluid to move
across the base AB, i.e.
4>1I(X,
0, t)
==
-f(x,
t). Torelli (1977 a) used
Baiocchi's approach and formulated the problem in an extended fixed
domain in space and time using the variable
w(x,
y,
t), where
w(x,
y,
t)
==
f
[<f;(x,
t+y--r,
-r)-(t+y--r)]d-r
in the domain 0 < x <
Xl>
0 < Y <
Y3,
0 < t <
T,
where
Xl
is
the
width of the
dam,
Y3
its height, and T some final value of time t >
O.
He
formulated
differential and variational inequalities and gave some theoretical results.
Friedman and Torelli (1977, 1978) established
the
regularity and physical
properties of Torelli's solution and proposed a finite-difference scheme.
Transient problems have been studied from
the
numerical point of view
by several authors including Taylor and Luthin (1969), Cooley (1971),
Neuman and Witherspoon (1971), Verma and Brutsaert (1971), Todsen
(1971), and Neuman (1975).
In a transient dam problem,
the
conserva-
tion condition
on
the
moving interface analogous
to
the Stefan condition
can be written
(2. 156a)
y
~~~
____________
~=-L-
______
X
A~I·
______ a
______
~·IB
FIG. 2.22. Unsteady flow through porous dam

Degenerate free-boundary
problems
91
where
.ex,
.e
y
,
.e
z
are
the
direction cosines
of
the outward normal
to
the
interface
on
which P = 0,
f3
is a porosity constant for
the
medium, and
lex,
ky,
kz
are directional permeabilities. France et al. (1971) and Taylor et al.
(1973) incorporated this boundary condition into finite-element schemes
for
both
transient and steady-state problems (see §8.2.2).
Meyer (1980) used Patel's (1968) form
of
boundary condition discussed
in
§1.3.9.
Thus
in
two space dimensions, for example,
and
substituting
l,.fly
= (ap/ax)/(ap/ay), (2.156a) becomes
k
apa</>
+
apa</>
=_
(apax
+
apa
y
)=
ap
x
ax
ax
ky
ay ay
f3
ax
at ay at
f3
at
(2. 156b)
on
the
surface p = 0 where also we have ay/at =
-(ap/at)
(ay/ap ). Thus
(2.156b) gives
af
1 [ ay ap
a</>J
1
at=-(j
-lex
ax
ax
+kyay
=(j[1ex(1-</>y)(a
y
/ax)2_ky</>y],
(2. 156c)
remembering
that
</>
= p + Y and with
the
free boundary denoted by
y = f(x, t). Meyer applied his method
of
lines (§4.3.4)
to
a transient dam
problem by using (2.156c).
Yet
another
form
of
moving-boundary condition was used by Comin-
cioli
and
Torelli (1979).
Thus
by writing
ap
(.
ap . a
p
)
(.
ax
. a
y
)
-=
'-+J-
.
'-+J-
'at
ax
ay
at at
(
. ap . a
p
)
(.
a</>
.
a</»
=-
'-+J-
.
'-+J-
ax
ay
ax
ay'
we obtain
Pt=P;+P;+Py
on
using </>=p+y.
(2. 156d)
Comincioli
and
Torelli (1979) considered
the
various numerical al-
gorithms
to
be
of a heuristic nature
and
not
sufficiently rigorous from a
mathematical point of view. Accordingly, they developed a new numeri-
cal algorithm based
on
a finite-element discretization
of
a variational
equality.
Formulated in terms
of
pressure and with reference
to
Fig. 2.22
the
equation
to
be
solved is
VVt
- V
2
p = 0 in O(t),
where
O(t)
is
the
flow region
O<x<a,
O<t<T,
O<y
<f(x,
t), Y = f(x, t)
is
the
free boundary,
and
a is
the
width
of
the
dam.
The
constant v is
the
retentivity coefficient
(v~O).
On
the
free boundary p = 0,
and
from
(2.156d),
p;+p;+py
=Pt>
while
on
the
faces of
the
dam, f(O,
t)~Yl(t),
f(a,
t)~Y2(t),
together with
p(O,
y,
t)=(Yl(t)-y),
p(a,
y,
t)=(Y2(t)-y),
p~O.
