Crank J. Free and Moving Boundary Problems

152

Analytical solutions

an

area A of the surface, a cylindrical hole will

be

formed, and

if

in a

time interval

8t the volume of material evaporated

is

A 8x then

hpA8x=W8t,

where h

is

the

heat required

to

vaporize unit mass of

the

material of

density

p, i.e.

dx/dt=

W/(Ahp).

(3.194)

This speed, dx/dt,

is

an upper limit for

the

rate

of

penetration which will

be

approached after a finite time

if

some conduction of heat into the

material occurs.

The

coupled process constitutes a Stefan problem in

radial coordinates. First, Andrews and Atthey

(1975a) obtained a pertur-

bation solution for a planar evaporating boundary using an expansion

parameter

e defined by

(3.195)

where

C

and

L are average specific

heat

and latent heat respectively and

Tv

is

the boiling point. They quote physical

data

to

justify taking s small

(s

- 0.2). Non-dimensional variables

r.=z/f,

T = vt/f,

g=

x/f,

are introduced where S is the Kirchhoff temperature variable, z is normal

to

the

evaporating surface z = x(t), v

is

the

speed of

the

boundary in the

evaporation-controlled limiting case, and

l

is

a characteristic length

defined by

f=K!(pCv),

(3.196)

where

K

is

an average conductivity over

the

temperature range (0,

Tv).

The

problem

is

then specified by the equations

(Up

/ar.

2

=

ao/aT,

dg/dT

-1-

s(ao/ar. + 1) = 0,

0=

1,

o

~

0,

Substituting the trial perturbation series for

0,

g,

1/

=dgJdT,

O(r.,

T)

=

Oo(r.,

T)+

e01(r.,

T)+

...

,

g(T)

=

gO(T)

+ eg1(T)+ .

..

,

1/(T) = 1/0(T) + S1/1(T) +

...

,

into (3.197) gives

to

zero order

a

2

o

%

r.

2

=

aoo/aT,

1/0=

1, 0

0

= 1.

(3.197)

(3.198)

Approximate solutions

153

Ignoring the time for the boundary

to

reach the evaporation temperature

(which can

be

shown

to

be

0(e

2

))

the zero-order solution,

~o=

'T,

(3.199)

comes by integrating the second of (3.198). Taking

the

Laplace transform

in a frame of reference moving with the boundary and putting 8

0

= 0,

'T

=0

gives

The

first -order equations

;i8

1

/a,2 =

a6

1

/a'T,

lead

to

and hence

(3.200)

'1/1

= 1

+a8ofa"

(3.201)

This solution

is

a good approximation for

'T

=

0(1)

but for

'T

= O(eZ) its

second term

is

0(1)

rather than O(e).

For

small times (3.201) provides an

outer solution which needs

to

be

supplemented by

an

inner solution that

allows for

the

pre-evaporation heating of the surface, initially at some

temperature below the boiling point.

During

the

pre-heating period

the

heat

conduction equation is still the

first of (3.197), which

is

to

be

solved for conditions

a8/a,=-1-1/e,

'=0

8=0,

'>0,

8~0,

,~OO,

The

standard solution (Carslaw and Jaeger, 1959)

is

8 =

(1

+ 1/e

){2('T/'7T)!

exp(-i,2/'T)_,

erfc@,,'T!)},

which gives a pre-heating time

'T;o:O.

'Tp=i'7Te

2

/(1+ef

(3.202)

that

is

0(e

2

).

The

temperature 8

p

("

'Tp)

is

6

p

= exp[

-{,(1

+

e)/'7T

1

e}2]-{C(1 + e)/e}erfc{C{1 +

e)/'7T!e}.

(3.203)

For

the early stages of evaporation (3.202) and (3.203) suggest

the

new

variables

" =

"e,

8'=8,

The

heat conduction equation becomes

a

2

6'

/aC'2

=

a8'/a'T'

154

Analytical solutions

with

the

boundary conditions

11'

= 1 +

a(J'/a{;'

+

e,

(J'

~

0,

(J'

= 1,

{'

~

co,

and the initial condition (3.203) becomes

(f

=exp[

-{{'(1

+ e)/1r!}2]-

{;'(1

+ e)erfc{r;'(1 +

e)/'IT~}

at

T'=-~'lTe(2+e)/(1+e)2.

The

zero-order perturbation solution based

on

(J'({',

T')

=

(Jb({;',

T')

+

e(J~

({;',

T')

+

...

,

l1'(T')

=

l1b(T')

+

el1~(T')

+

...

must satisfy the equation

and

the

conditions

(3.204)

(3.205)

For

very small times, i.e.

T'

=

0(e

2

),

the

evaporating boundary

will

have

moved only a small distance from

{;'

=

O.

We

therefore temporarily

discard the condition for

l1b

on

{'

= 0 and solve the resulting problem for

(Jb

on fixed boundaries. AftelWards,

the

discarded condition can

be

used

to

determine

the

motion of

the

evaporating boundary. Thus by taking

the

Laplace transform of (3.204) and using

the

conditions (3.205) except

the

one

for

l1b

we obtain for

the

transform, iib(p) ,

d

2

iiMd{;,2=

piib-exp(-{;'2/'IT)+{;'

erfc({;'/'IT!),

(3.206)

iib

= 1!p,

(,=O,

iib

~

0,

The

solution of (3.206) obtained by using Green's functions and

then

integrating by parts

is

iib

=

fexpC~1Tp

)[2 exp(

-p~{;')erfGp1T)!

+

exp(p!{;')erfc{{' I

'IT!

+

!(p1T

)!}

-exp(

-p!{;')erfc{{'

I'IT!

-!(P'IT

)!}]p-~

+

+ (1!p)exp( -(;'2/'IT)-

({;'

Ip

)erfc(r;'

/~).

(3.207)

The

Laplace transform applied to

the

discarded condition for

l1b

gives

iib =

lip

+

aiiMa{;'

at

{'

= 0 and substitution for

aiiMa{;'

from (3.207) finally

yields

Approximate solutions

155

Inversion by the convolution theorem gives

an

inner solution

TJ'

= (2/7r)arc

sin{(1

+llTh-T~}+O(e).

(3.208)

Andrews and Atthey

(1975a) use a standard matching principle to

construct

the

uniformly valid approximate solution

TJ

= [1 +

eG

erfcGT~)-

("Tl'T)-!e-%>}][(2hr)/{1 +

e/("Tl'T)!}]

x [arc sin{(1-f1Te

2

/T)!}],

(3.209)

which has errors of O(e) when

T=0(e

2

)

and of

0(e

2

)

when T

=0(1).

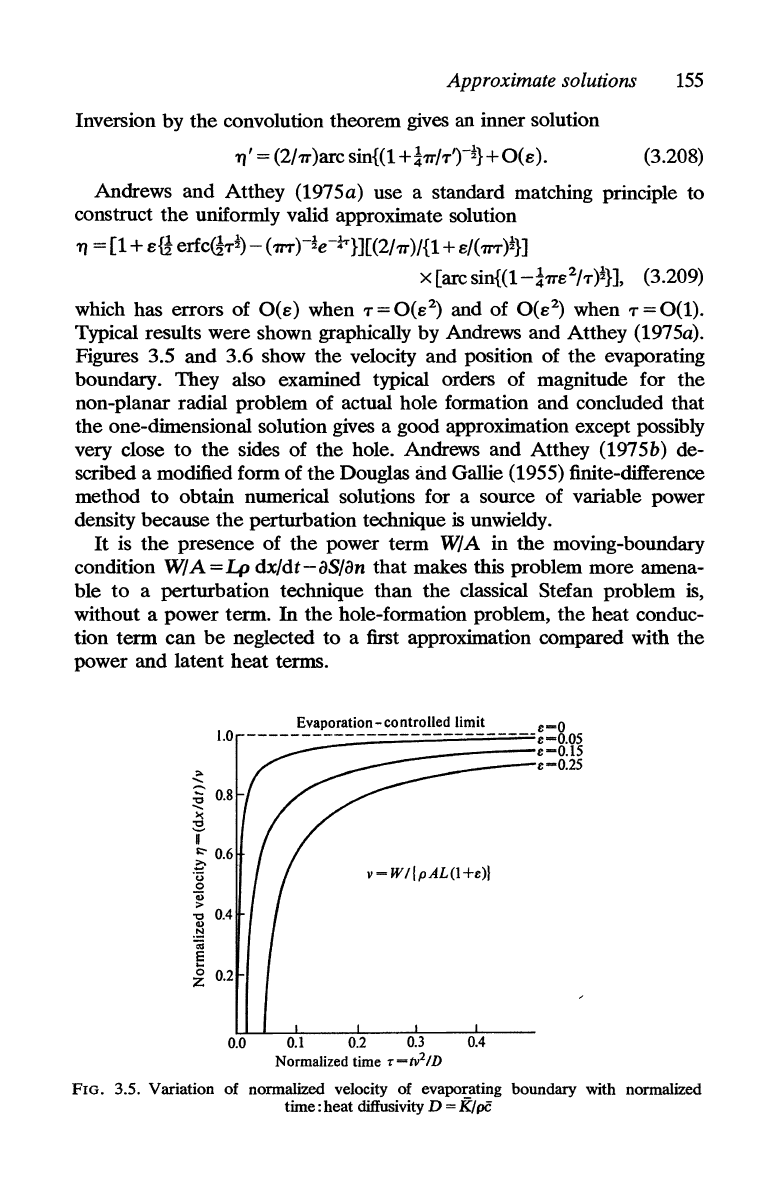
Typical results were shown graphically by Andrews and Atthey (1975a).

Figures 3.5 and 3.6 show the velocity and position of

the

evaporating

boundary. They also examined typical orders of magnitude for the

non-planar radial problem of actual hole formation and concluded that

the one-dimensional solution gives a good approximation except possibly

very close to the sides of the hole. Andrews and Atthey

(1975b) de-

scribed a modified form of the Douglas and Gallie (1955) finite-difference

method

to

obtain numerical solutions for a source of variable power

density because

the

perturbation technique is unwieldy.

It

is

the

presence of

the

power term

WI

A in the moving-boundary

condition W/A

=Lp

dxldt-iJSliJn that makes this problem more amena-

ble

to

a perturbation technique than

the

classical Stefan problem is,

without a power term. In

the

hole-formation problem,

the

heat conduc-

tion term can

be

neglected to a first approximation compared with the

power and latent

heat

terms.

Evaporation-controlled limit

e-O

1.0

---------------------------e=o.o5

""

......

~

0.8

......

><

~

I

""

0.6

~

'u

o

0:;

>

'0

0.4

Q)

.t::!

OJ

E

o

;Z

0.2

~-----e-0.15

~---e-0.25

v-wllpAL(l+e)}

0.0

O.l

0.2

0.3

0.4

Normalized time

r-tv

2

lD

FIG. 3.5. Variation of nonnalized velocity of evaporating boundary with nonnalized

time: heat diffusivity D

=

KIP;;

156

Analytical solutions

~

0.4

.....

~

o I

5""

:E

~

0.3

~-a

","0::

"t:I ::;

Q)

0

N.Cl

~

~0.2

§

''-::

o e

z

8-

'"

~

0.1

0.2

0.3

Normalized time

-r-tv

2

/D

e=0.05

e-0.15

e-0.25

0.4

FIG. 3.6. Variation of nonnalized position

of

evaporating boundary with nonnalized

time: heat difiusivity D

=

Kt

pC

Oi)

Stefan's problem for a sphere. The detennination of the time taken

to

complete

the

inward solidification of a molten sphere, initially at

the

fusion temperature, presents mathematical difficulties. For example,

the

analyses by Pedroso and Domoto (1973) and by Riley, Smith, and Poots

(1974) break down before the centre freezes. Stewartson and Waechter

(1976) developed a complete asymptotic theory for large latent heat

which adequately describes the final temperature profile and they also

detennined the first four terms of

the

asymptotic expansion of

the

time

to

complete freezing. We outline here

the

essential features of their ap-

proach. More manipulative detail

is given by Stewartson and Waechter

(1976).

The liquid sphere

O:s:;;

r*:s:;;

a

is

at

the

fusion temperature n throughout

and

at

time t* = 0 the surface temperature

is

dropped

to

and maintained

at

T\t.

Convection and density changes

on

solidification are neglected as

usual, and radial heat

flow

is

assumed. Non-dimensional variables are

defined

to

be

r=

r*/a,

S=S*/a,

T*-n

r*

8(r,

t)=

T*-T*

-,

F w

a

where S*(t*) denotes the solidification boundary and

K,

p, c are heat

conductivity, density, and specific heat respectively.

The

problem

is

then

Approximate solutions

157

defined

by

the

equations

(;20/or

2

=

(1/A)

oO/ot,

S(t)<r<1,

S(O) = 1, 0(1,

t)=-1,

t>O,

O(r,

t)

~

0,

oO/or

~

S dS/dt, r

~

S(t)

(3.210)

in

the

solid phase, and

A

=L/{c('n!-T~)}.

Here

L is

the

latent heat and we take

A»

1.

AB

in

the

earlier papers

Stewartson

and

Waechter

put

co

a(n)(t)(1-

r)2n+l

0(r,t)=-1+L

An(2

1)'

n=O

n+.

(3.211)

where

aO(t) =

a(t)

and a(n), n = 1, 2,

...

, are

the

successive derivatives of

a function

a

to

be

determined. Use of

the

boundary conditions

on

r =

S(t)

leads

to

equations

co

a(n)(t)(1-

S)2n+l

n~o

A n(2n +

1)!

1,

f

an(t~(1-

~)2n

-SS(1) (3.212)

n=O

A (2n).

and by writing

co

S = L A

-ns,.

(t), a = L A

-n<Xn(t),

(3.213)

n=O

where

So(O)

= 1,

s..

(0)

=

0,

n ;;;'1, substituting into (3.212) and equating

successive powers

of

A

-1

to

zero we find

-tS~+iS~

=

t-~,

1 1 13 1

SI

=

6S

o

(1-

So),

S2

= -

72S~

-

360S~

+ 20S

o

'

(3.214)

1 607

29

149

S3

=

432S~

+ 45360Sri

11340S~

,

with corresponding formulae for a,.

The

first of (3.124) shows

that

near

t=~,

So={2(~-t)}~

approximately and hence

the

first approximation

to

the

time t =

tE

at

which s = 0 and

the

sphere is completely frozen is

tE

=~.

The

other

relationships in (3.214), however, show that

the

expansions

(3.213)

break

down when

S~-

A-I and an inner rescaled solution is

needed.

The

form of

Sn

near

t = t needed

to

match inner and

outer

158

Analytical solutions

solutions is seen, in terms

of

1/

=

2(1-

t),

to

be

So

=

1/!

+ h +

O(

1/

1

), S =

6~~

-~+

O(

1/!)'}

1 1

_1

S2

=

-n1/C

451/

+0(1/

2).

(3.215)

To

obtain an inner solution Stewartson

and

Waechter (1976) introduce

a = 1 + A!A(A, x),

S = A

-~Y(A,

x)

(3.216)

and express

the

conditions (3.212) as

A

(1)

A

(2)

Y =

A(1-

A

-!y)

-31

(1-

A -!Y)3

+51

(1-

A

-~y)s

+

...

,

(3.217a)

where

the

differentiation is with respect

to

x,

and

{

A

(1)

A

(2)

}

yy(1)=

1+A

-!

A

-2!(1-A

-!Y)2+T!

(1-A

-~Y)4+

.....

- (3.217b)

In

terms

of

intermediate variables

(A,

x),

'I'(A, x) defined as

A

(1)

A

(2)

(-1)"A

(,,)

(A,X)=A-T!+T!+"'+

(2n+1)!

+

...

,

(3.218)

A

(1)

A

(2)

(-1)"A

(,,)

'I'(A,X)=A-2!+T!+"'+

(2n)! +

...

,

(3.217) reduce

to

Y(A,

x)

=

<1>-

A~Y'I'-

A-I

;;

<1>(1)

+ A

-~

;-;

'\ft<1) + A

-2

~;

<1>(2)

+

...

'}

y2

y3

yy(1)

= 1 + A -!'It + A-I Y

<1>(1)

- A

-~

2! '\ft<1) - A -2

3T

<1>(2)

+

....

(3.219)

Starting with

the

second of (3.219)

and

putting all terms

O(A

-!)

to

zero

gives Y - (2x

)~;

then

from

the

first equation

= (2x)! and

'I'

follows from

(3.218).

The

expression for Y is

then

corrected

to

include terms

O(A

-!)

and

the

cycle repeated.

By

taking Laplace transforms

of

(3.218), Stewart-

son

and

Waechter deduce after some manipulation

that

'I'(A,

x)

=

(A,

x) - 2 f

{""(I)(A,

z)exp[

-n

2

'lT

2

(z -

x)]

dz.

,,=1

(3.220)

Approximate solutions

159

They

then

substitute

the

expansions

<1>:

<1>0

+

)..

=:<1>1

+

)..

=:<1>2

+

...

, }

'1'-'1'0+)"

~1+)..

'1'2+···,

Y=

YO+)..-~Y1+)..-1Y2+

...

'

into (3.217)

to

obtain

Yo

Y'd-)

= 1,

Yo

= (2x)i,

<1>0=

Y

o

=(2x)!,

d

dx

(Y

o

Y

1

) ='1'0,

<1>1

= Y

1

+

Yoqro,

d~

@

Yi

+

Yo

Y

z)

=

'1'1

+ Y

o

<l>&1),

(3.221)

(3.222a)

(3.222b)

(3.222c)

(3. 222d)

(3.222e)

<1>2

= y

2

+qro

Y

1

+ Y

O

qr1-!Y5<1>&1>,

etc. (3. 222f)

By

using

the

Laplace transform

of

(3.220) with

<1>0=

(2x)~,

the

asymptotic

expansion

of

the

'1'0

as x

~

0 is found

to

be

qro(x) -

-(21T)-~'Y

+

In(1/x1T2)},

(3.223)

where

l'

= 0.5772

...

is Euler's constant. Then (3.222c) gives

(3.224)

as

x~o,

and

(3.225)

follows from (3.222d) as x

~

O.

Inspection reveals that Y

1

/Y

O

~

00

as

x

~

0 and it is likely

that

the

expansion (3.221) breaks down when

g =

0(1),

where g =)..

-~

In(1/x), which implies through

t~e

second of

(3.216) that

the

inner solution fails within a time

O()"

-1

e

-A') of

the

time

for complete freezing. Subsequent analysis confirms these limits but

meanwhile we can write

( )

l{

3g 1 -

-1

<1>-

2x'

1-2(21T)~+···

2(21T)..)!(1+'Y-6In1T+

...

)+O().. )

(3.226)

as x

~

0 for fixed

g,

where higher powers of g have been omitted.

By studying

the

behaviour

of

Y,

<1>,

and

'I'

as

x

~

00,

Stewartson and

Waechter (1976) arrive

at

results for

the

inner solution which agree with

the

two-layer analysis

by

Riley et al. (1974) with a trivial correction. They

160

Analytical solutions

find that as

x~oo

(3.227)

where 8

1

=

(2/7rS)!C(3)

and C is

the

Riemann zeta-function, and develop

an expansion for

tE

in

the

form

=

tE

= i+ L

b,.A

-",2

(3.228)

n=2

with

where

and

q,1

is defined by (3.222d). A further stage

of

matching yielded

b

s

=-2

f

21

2

r=e-

a

q,2(

:

2)da

n=l

n

7T

.10

n

7T

but

a numerical value was not determined.

The

terminal temperature

distribution

n was found

to

be

given by

1

1.

~

sinmrr

-1

+-(27T/A)2

I.J

--z--2

r

n=l

n

7T

--1--(2/7TA)i

In(2sinh)dy.

(3.229)

1

J,-

r7T

0

This expression predicts

that

T~

has a logarithmic singularity as r

~

0

whereas

T~

=

J1;

from

the

boundary conditions. This non-uniformity

stems from

the

behaviour of Y

1

/Y

O

as x

~

0 and

the

breakdown of

(3.221) referred

to

above.

Stewartson and Waechter (1976) examine further

the

properties of a

terminal core

of

exponentially small radius by using

~

= A

-~

In(1!x) =

A

-il

n{1/A(t

E

-t)}

as independent variable instead

of

x.

In

order

to

obtain

a uniformly valid expression for

n correct

to

order A

-~

they write

q,=

(2x)~[F~(~)+

A

-~F~(~)+

.

..

],

Y =

(2x)i[Go(~)+

A

-!G1(~)

+

...

],

(3.230)

where

Fm

G

n

are functions of

~

to

be

found and differentiation is with

Approximate solutions

161

respect to

~.

Some analysis leads

to

a parallel expression for

'\f1

which

is

A~

'\f1~-

(21T)f

Fo(~)+

(21T)~F1(~)+(2In

2-2)F~W-1'-2In

21T}+O(1).

(3.231)

The unknown functions

Fn>

G

n

are now found by substitution of (3.230)

and (3.231) into (3.219) and solving the ensuing differential equations.

On

writing Z = 1 + S2(21T)t their expressions for n = 0, n = 1 become

Go(~)

=

Z-t,

Fb(~)

=

G~,

-1

G1(~)

=

2(21T)!Z2

[1'+

1-21n

1T+(5-6In

2)lnZ],

FH~)

=

2(2:~~Z4[1'+l-2In

1T+(5-6In2)lnZ].

These are used in the expression

8=-r+A-i[(1-r)+2

n~l

n1Tsinn?Tr

1""(y)exp{-n21T2(Y-X)}dY],

obtained by them previously in

the

derivation of (3.229), to give in

particular

(

21T)f

~

sin

n?Tr

8(r,

tJ:J=-r+

- i.J

~

A

n=l

n

1T

X

[F~(N)

+ A

-~Fl

(N) - (2 -

l'

-

2ln

2)F

o

(N)}], (3.232)

where N = A

-i

In n

2

1T2.

The

evaluation of (3.232) is carried out by using a

theorem by Zygmund (1959) and shows that

the

terminal temperature

8

E

= 8(r,

tJ:J

satisfies

iJ8

E

1 1 [(5 -

6ln

2)ln(1 +

R)]

Tr-

(1

+ R)2 +

(21TA)!

(1

+ R)3 +

...

, (3.233)

where

R =

(21TA)-!

In(1/?Tr).

When

R«

1

iJ8

E

2

(1)

Tr--

1

+

(21TA)!ln

?Tr

'

which

is

in agreement with (3.229) when

r«

1, so that a composite

exp~ession

for 8

E

,

uniformly valid for all r < 1,

is

now available. The

boundary condtions which imply 8

E

= 0 at r = 0 and, from the definition

of

8,

iJ8/iJr

= 0 at r = 0 are seen

to

be

satisfied by (3.232) since

the

right-hand side of (3.233) approaches zero as R

~

00.

Soward (1980) obtained the same key equations for the sphere as

Stewartson and Waechter (1976) by using a method of images which

Crank J. Free and Moving Boundary Problems

Подождите немного. Документ загружается.