Crank J. Free and Moving Boundary Problems

232 Fixed-domain methods

TABLE

6.1

Values

of

10

3

u at x = 0.5, y = 0 for model problem

(Furzeland 1977b):

Cl

=4,

C2=

1,

kl

=2,

k2= 1, A

=2;

v(H)

signifies a discontinuous enthalpy function

and

H(

v)

a smoothed function

Time

0.2 0.4 0.6 0.8 1.0

v(H)

h = 0.1, 8t = 0.04

-421

-208

-34

39

102

H(v), 8

=0.001

h = 0.1, 8t = 0.04

-412

-197

-22

44 103

H(v), 8 =

O.OS

h=0.1,8t=0.04

-416

-196

-43

38 107

v(H)

h =

O.OS,

8t = 0.01

-421

-202

-S3

46

110

H(v), 8 = 0.01

h =

O.OS,

8t = 0.01

-417

-191

-Sl

47

l1S

H(V),8=0.03

h =

O.OS,

8t = 0.01

-421

-199

-S2

47

113

Exact solution

-420 -199

-Sl

48

l1S

rewritten as the single equation

a a

2

v

at

H(u(v))

= ax2

+f(u(v)),

(6.49)

where

v(u)

is defined by (6.8) and H

is

the discontinuous enthalpy

function

H(u)

=

t:

C(8)d8+{~

if

(6.50)

and

u*

is

a reference temperature.

The

parameters K,

C,

f represent

Kl>

Cl>

it

if

U<UM

or

K

2

,

C

2

,

f2

if

U>UM,

and

u(v)

is

the inverse

transformation

of

(6.8). Equation (6.49)

is

approximated by

(6.51)

where r

= Ilt/(IlX)2, 8

is

the implicit, time-discretization parameter, and

aj=

Hj+

Ilt(1-

8)fj+

r(1-

8)(Vj_1-2vj+vj+1)'

(6.52)

A point, successive over-relaxation scheme (SOR)

is

used

to

solve (6.51)

for

vj+l,s+1

by treating

the

right-hand side, bj, as known at

the

s.

The reiax&tion parameter

Cd

is varied automatically according

to

the proportion of phase 1

to

phase 2 (Elliott 1976).

The

standard discussion of

Cd

for a linear system gives

the

optimum

Enthalpy method

233

value for a matrix

cI

+

OA

cSt/(cSx?

to

be

2

205t

w = 1

+(1-p2)~'

P

=-c-cos

7TcSX.

The

relevant matrix in (6.51) is c(v)+OA5t/(cSx? with c(v) a diagonal

matrix with entries

l/Kl

or

1/K2 for the frozen or melted regions

respectively. Near the solution at time

(n + 1)

cSt,

c(v)

is

approaching

c(v

n

+1)

and so Elliott (1976) calculated w from the usual expression with

the diagonal entries in c given by

Z/Kl

+(1-

z)/K

2

,

where z is the

proportion of mesh points in the frozen region, phase 1.

For

mesh points j where the phase change

is

occurring, w

is

set equal to

unity following Meyer (1973).

At

each point j, an inner iteration (p

=:

1,2,

...

) is performed based on a Newton linearization of (6.51), i.e.

V!'+l,p+l

=

vn+l,p+

b

i

-{H

+2r6v -

Of

at}j+l,p (6.53)

I j {dH/dv + 2r6 - 0 ;1t df/dv}j+1,p

TABLE

6.2

Moving boundary position s(t): two-phase Stefan problem

(Bonacina et al.

1973);

kl

= 2.22, k2 = 0.556,

Cl

= 1.762,

C2 = 4.226, ,\ = 338; zero melting temperature, surface temp-

erature

-20,

initial temperature 10. Starting time t = 0.0012

with s(t)

=0.015

975;

at=O.0012

except for method (iii)

and

smoothed enthalpy results

Time

0.0024 0.0036 0.018 0.072 0.144

0.288

(i)

0.0224 0.0276

0.0618 0.1238 0.1750

9·2476

(ii)

(0.0220) (0.0273)

0.0196

0.0256 0.0617

0.1236 0.1749 0.2474

(iii)

0.0228

0.0279

0.0619 0.1237

0.1750

0.2474

(iv)

0.0250 0.0250

0.0500 0.1250 0.1750 0.2490

(v)

Non-monotonic values near

(0.180) (0.247)

phase change 0.1391 0.1791

0.2389

Exact

solution

0.0226 0.0278 0.0619 0.1238 0.1750 0.2475

(i)

Method of lines in tinle with invariant inlbedding (Meyer 1970;

Furzeland

1979b):

81

space points, 6

=!.

(ii) Boundary-fixing coordinate transformation (Crank 1957a); 41 points

in each phase, 6

=!;

6 = 1 for values in parentheses.

(iii) Boundary-fixing transformation and method of lines

in

space by

Elliott reported in

Funeland

(1979b);

41

points in each phase,

ODE

in

tinle.

(iv)

Enthalpy method:

41

points, 6

=~,

stepwise behaviour can

be

cor-

rected by Voller and Cross's (1981a) procedure.

(v)

Smoothed enthalpy (Bonacina et

al.

1973):

81

points,

At

= 0.0004,

B = 0.5, results in parentheses started at t = 0.072;

if

started at t = 0.0012

non-monotonic instability occurs near phase-change boundary.

234 Fixed-domain methods

is used, where the

SOR

superscript s has been dropped and

dH/dv

= (dH/du)/(dv/du),

df/dv

= (df/du)/(dv/du).

Non-linear conditions

on

the

fixed boundaries are similarly treated by

Newton linearizations. Denoting the converged result of (6.53) by

ilj+l,

the

outer

SOR

iteration

is

written

(6.54)

Elliott (1981) established the convergence

of

this

SOR

scheme for

6 <

w

<2

if

w = 1

is

used when

vj+l

. vj+1,s

~O,

i.e. a mesh point changes

phase.

TABLE

6.3

Moving boundary position

and

surface concentration:

oxygen diffusion problem. Upper value =

u(O,

t); lower

value = s(t)

(i)

201 points

8=~,

At=O.OOl

(ii)

41 points

8=~,

At=0.005

(iii)

41 points

ODE

time

(iv)

41 points

8=~,

t=0.005

*Hansen and

Hougaard (1974)

* Ferriss and Hill

(1974); boundary

fixing; 40 points,

&=0.0005

Ferriss and Hill

(1974); embedding

8t=0.01

Time

0.04 0.10 0.18 0.19

0.2746 0.1436

0.0222 0.0090

0.9993 0.9361

0.5065

0.3541

0.2770

0.1437

0.0219

0.0091

0.9991 0.9349

0.5023

0.3495

0.2745

0.1433

0.0219

0.0091

0.9992 0.9358

0.5028

0.3477

0.2766

0.1439

0.0221

0.0093

1.0000

0.4750

0.3250

0.2743

0.1432

0.0218

0.0090

0.9992 0.9350

0.5011

0.3454

Time

0.02 0.10 0.12 0.16 0.18

0.3417

0.1438

0.1097

0.0493 0.0222

1.0000 0.9354

0.8800

0.6850 0.5046

0.3404

0.1437

0.1091

0.0488

0.0218

1.0000 0.9353 0.8797 0.6860 0.5097

Methods (i-iv) as

in

Tables 6.2 with the amended parameters

indicated. Solutions start from

t = 0.0025 except for those bearing

an asterisk which start from

t =

O.

Enthalpy method

235

Furzeland (1980) compared results obtained by the enthalpy program

for several test problems with those obtained by other methods. Tables

6.2, 6.3 are extracted from his paper and some other results referred

to

in

this book are assembled there for convenience.

6.2.5. Accurate determination

of

phase-change boundary

It

is a central feature of the enthalpy method that the position of the

phase-change boundary is determined,

a

posteriori,

from

the

numerical

solution carried out in a fixed domain. Simple inspection of the solution

reveals which mesh point

is

undergoing a phase-change at any time and it

may

take

several time steps for the change to be completed there. The

position of the boundary can be bracketed by the two mesh points

between which temperature changes from less than to greater than the

phase-change temperature

or

vice versa. To locate

the

boundary more

accurately, however, can present difficulties. Extrapolation of the temper-

ature values,

u

or

v,

from either side of

the

phase boundary,

or

interpola-

tion across the boundary,

is

a possible refinement but the results tend to

exhibit a physically unrealistic, stepwise behaviour in

the

motion of the

boundary and in the time history of

the

temperature at a typical fixed

point.

Voller and Cross (1981a) advanced explanations of

the

stepwise and

oscillatory behaviour of

the

basic enthalpy solutions both for discontinu-

ous

and

smoothed enthalpy functions.

The

authors proposed an interpre-

tation of

the

numerical solution which leads to a more accurate evaluation

of

the

boundary movement and

the

temperature history at any point.

With reference first

to

a one-dimensional solidification problem with a

discontinuous enthalpy function, Voller and Cross (1981a) considered an

element

e;

of

the

discretized region associated with a mesh point or node

i.

The

total heat in this element at any time

is

approximated by

II.

8x,

where

II.

is

the enthalpy at node i and 8x

is

the element length (Fig. 6.3).

If

at

any time t the freezing front

is

in element

e;

and moving towards

element

e;+1,

the total heat in

e;

is

the

sum of the heat in the solid and

I

+

ej

Solid : Liquid

I

~fax-l

I

-----

ax

----

FIG. 6.3. Partially frozen element e

j

236

Fixed-domain methods

liquid parts, and so

If;

can

be

approximated by

If;

=

CuJ+(Ct4

+L)(l-f),

(6.55)

where

f is

the

solid fraction

of

the

element

and

the

heat

capacity C is

taken

to

be

the

same

in

both

phases.

When

the

freezing front reaches

the

node

i then

f=!,

U;

=

UM,

the

melting temperature, and (6.55) becomes

(6.56)

Thus, when any nodal enthalpy satisfies (6.56)

the

phase-change

bound-

ary can

be

located approximately

on

the

node

i.

This interpretation

of

the

state

of

an element undergoing a phase-change is physically

more

satisfying

than

the

idea

that

the

whole element is uniformly in some

intermediate

state

betwen

the

solid and liquid phases.

Voller and Cross

(1981a) concluded from (6.56)

that

if

at

any nodal

point

i in

the

basic finite-difference solution H/>CuM+!L and

Hj+l<

CuM+!L, for a freezing problem,

the

phase-change boundary

had

passed

through node

i in

the

time interval between j 8t and

(j

+ 1) 8t.

It"it

is

further assumed

that

the

enthalpy changes linearly in any time interval,

8t,

then

the

time

t;

when

the

phase-change boundary is

on

node

point

i,

which occurs when

If;

=

CuM

+ !L, is given

by

t;

=

(j

+

a)

8t

where

a < 1

and

is estimated

by

a=@L+Cu

M

-Hl)/(H/+1-HD. (6.57)

Clearly,

at

time

t;

the

temperature

at

node i is

UM'

The

temperatures

at

other

node points k

(k1=

i)

are

approximated

by

the

linear

int~rpolation

(6.58)

Voller and Cross

(1981a)

obtained

good agreement between

their

finite-

difference solution

interpreted

using

the

above argument

and

the

analyti-

cal solution for a classical, two-phase Stefan problem.

They

extended

their

algorithm

to

include some two-dimensional problems

and

used

it

to

solve a problem similar

to

the

freezing in a square channel studied

by

Crowley (1978),

but

it was a two-phase

problem

as distinct from Crow-

ley's

one

phase. A refinement

of

the

method

(Voller and Cross 1983)

led

to

a

more

continuous tracking

of

the

phase change.

Voller and Cross

(1981a) also described

an

implicit scheme for numeri-

cal solution which incorporated

the

idea

of

choosing each

time

step so

that

the

phase-change

boundary

moved from

one

node

point

to

the

strategy adopted

by

Douglas

and

Gallie (1955),

but

they

did

not

apply

it

to

an

enthalpy

equation

(see

§4.3.1).

The

advantage

of

this approach is

that

the

position

of

the

phase-change boundary is known at each time step. This means

that

the

finite-difference formulae,

and

hence

the

nodal enthalpy and

temperature

Enthalpy method

237

distributions, have their normal accuracy and

if

the

heat

parameters are

different

in

the

two phases they can

be

easily

and

accurately accommo-

dated in

the

scheme.

The

essential feature

of

the

algorithm proposed is

to

ensure

that

at

each time step

one

and

only

one

nodal enthalpy has

the

value CuM+!L.

If

at

time t

the

phase-change boundary is

at

node

k,

an

initial guess for

the

next time step,

l>t

k

,

is

taken

as

l>tg

=

l>t

k

-

1

•

An

implicit finite-difference

scheme for equation (6.37), following Longworth (1975) (see equations

(6.36, 37) above) is used

to

evaluate

the

nodal enthalpies for a time

intervall>tg

and

for successive estimates,

l>tl:',

calculated from

the

iterative

formula

(6.59)

where w is a relaxation factor.

When

H~~8{r

has converged

to

CuM+!L,

the

corresponding enthalpy

and

temperature values

at

all nodal points are

adopted as

the

solution for

the

time

t+l>tl:'.

Voller

and

Cross (1981a)

quoted

acceptable results for a simple two-phase freezing problem and

for a spot-welding problem similar

to

that

studied by

Atthey

(1974).

Their

implicit algorithm is much faster than

their

explicit

one

because

there

are

no

stability restrictions

on

the

time step.

Voller

and

Cross (1981b) confirmed that

their

explicit numerical

scheme incorporating (6.56-8) can

be

satisfactorily applied

to

the

freezing

or

melting

of

a circular cylinder.

From

a collection

of

numerical results

they approximated

the

dimensionless solidification time

t~

of

a circu-

lar

cylinder

to

be

given by

the

empirical expression

t~

=

(0.14+0.085u~)+(0.252-0.0025u~)L

*, (6.60)

with

an

accuracy of 1

per

cent

of

the

numerical predictions when

O:SO;

u~:so;

2,

2:so;L

*:so;50.

The

cylinders

of

radius R are solidifying

under

the

following conditions:

U=UO>UM,

O:SO;r:SO;R,

t<O;

U=UW<UM,

r=R,

t;a>O;

UM

is

the

melting temperature.

The

non-dimensional variables in

(6.60) are defined

to

be

t*=Kt/(R2pc),

u~=(Uo-U~/(UM-UW)'

L*=

L/{C(UM- uw)}.

The

enthalpy function has a discontinuous jump L

at

U =

UM'

A

more

tentative approximation for

the

melting time

of

general

symmetrically shaped

but

not

necessarily circular cylinders is based

on

an

upper and a lower bound.

The

former is

the

melting time

of

a circular

cylinder with

the

same cross-section as

the

original cylinder;

the

latter

is

based

on

a circular cylinder which fits totally inside

the

original cylinder.

A reasonable approximation for

the

solidification time

of

any general,

symmetrically shaped cylinder is afforded

by

using

an

approximating

circular cylinder with a radius equal

to

the

mean

of

the

radii associated

with

the

upper

and

lower bounds.

The

sum

of

the

percentage errors in

the

238

Fixed-domain methods

upper

and lower bounds

is

stated

to

be

given by B =

100(T~-

T~)fTa,

where

To>

Te

are the radii of the upper and lower bound approximating cylinders

and

Ta=(Tu+Te)/2.

For

a square channel

B=24

per

cent: for a pentagon

B = 14.5

per

cent.

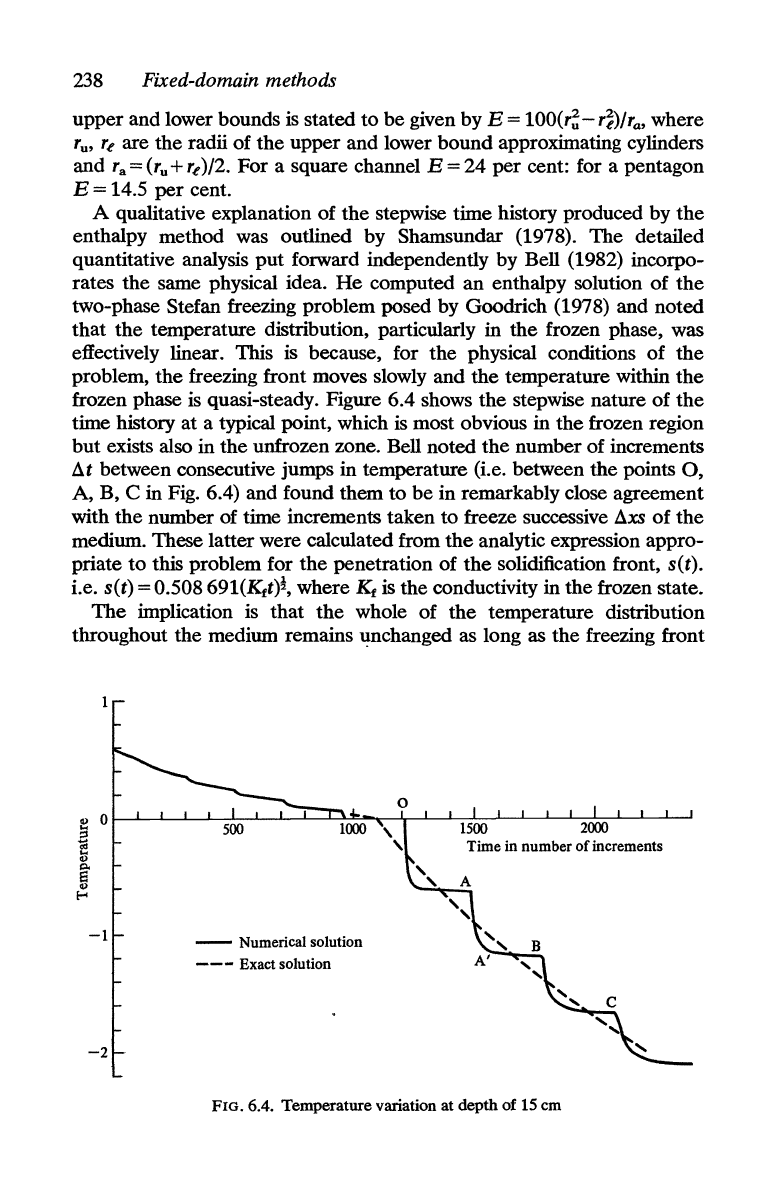
A qualitative explanation

of

the stepwise time history produced by

the

enthalpy method was outlined by Shamsundar (1978).

The

detailed

quantitative analysis

put

forward independently by Bell (1982) incorpo-

rates the same physical idea.

He

computed

an

enthalpy solution

of

the

two-phase Stefan freezing problem posed by Goodrich (1978) and noted

that

the temperature distribution, particularly in

the

frozen phase, was

effectively linear. This is because, for the physical conditions

of

the

problem,

the

freezing front moves slowly and the temperature within

the

frozen phase

is

quasi-steady. Figure 6.4 shows

the

stepwise nature of

the

time history at a typical point, which is most obvious in

the

frozen region

but exists also in the unfrozen zone. Bell noted the number

of

increments

at

between consecutive jumps in temperature (i.e. between the points

0,

A,

B, C in Fig. 6.4) and found them to

be

in remarkably close agreement

with the number of time increments taken

to

freeze successive

axs

of

the

medium. These latter were calculated from

the

analytic expression appro-

priate

to

this problem for

the

penetration of

the

solidification front, s(t).

i.e. s(t) = 0.508

691(Ktt)~,

where

Kt

is the conductivity in the frozen state.

The

implication is

that

the

whole of

the

temperature distribution

throughout the medium remains

~nchanged

as long as the freezing front

-1

- Numerical solution

---

Exact solution

-2

FIG.

6.4. Temperature variation at depth of

15

cm

Enthalpy method

239

remains within

the

spatial element

ax

associated with a particular mesh

point. A change in temperature only occurs when the front moves from

the

locality of one mesh point

to

the

next. This is exactly

the

behaviour to

be

expected from

the

quasi-steady temperature profile. Thus,

if

the

interval (m

-1)

ax';;;x

.;;;(m

+1)

ax

is changing from liquid

to

solid, the

enthalpy computed

at

the

point m

ax

lies between 0 and L, and the

temperature

at

m

ax

stays

at

zero. Thus, there is a region with fixed

boundaries, namely x

= 0, where

the

temperature is

-10°C

in Goodrich's

example,

and

x = m

ax

where

the

temperature is O°C.

The

analytical

expression for the temperature in this subsidiary heat-Bow problem

(Carslaw and Jaeger 1959, p. 100) has

the

form

(

x)

f .

mrx

(-n

2

7T

2

K

f

t')

-10

1---:-

+

£."

An

sm~exp

2(A)2

'

m

~x

n=l

m

~x

m

~x

where t' is measured from

the

instant the temperature

at

x = m

ax

becomes zero.

The

series represents

the

transient

part

of

the

solution.

The

term

-10(1-

x/m

ax)

is

the

ultimate steady state achieved theoreti-

cally after infinite time

but

for this problem the transient effects are very

short lived.

The

intervals

of

time over which transient

heat

Bow

occurs

are

the

short periods

of

rapid temperature drop in Fig. 6.4, e.g. between

the

points A and

N.

The

near-constant-temperature plateaux, e.g. be-

tween

A'

and B, indicate

the

period

of

the

steady-state

Bow.

Bell also showed, with

the

aid

of

the

analytical expression,

that

the

time-scale

of

the

transient effects increases in comparison. with

the

time

taken

for an element

to

freeze, as m increases. This is confirmed in Fig.

6.4.

There

is an implication for

the

linear interpolation which Voller and

Cross

(1981a) used as described above

to

determine

the

time

at

which the

enthalpy is

1L.

It

is

that

the accuracy will deteriorate when a point well

below the surface freezes, because

the

time increments for

the

element

to

freeze will

be

larger, and non-linear transient effects more significant.

6.2.6. Body heating

There

is an important class

of

problems in which

the

heat

needed

to

produce melting comes from

heat

sources distributed throughout the

volume of

the

material

rather

than

by entering through

the

outer

bound-

aries.

An

example is joule heating associated with electric currents within

the

medium. In such cases

the

melting does

not

necessarily take place

across a surface as in the classical Stefan problem. Instead, there may

be

an

extended region the whole

of

which is

at

melting temperature, and the

solid and liquid phases coexist.

This volume of material is called a 'mushy'

region, a

term

used by Tien

and

Geiger (1967) in relation

to

alloys. The

physical nature of a mushy region has been discussed more generally in

240

Fixed-domain methods

o

H

K

FIG. 6.5. Cross-section

of

a weld specimen

§1.3.1(iv). For the purpose of

the

present enthalpy formulation it suffices

to

say that within the mushy region

the

average enthalpy lies somewhere

between its values for the solid and liquid states at

the

melting tempera-

ture.

Atthey (1974) described an enthalpy method

to

solve a welding prob-

lem in which a mushy region occurs.

The

spot welding of two sheets of

equal thickness placed face to face

is

effected by passing a high electric

current between two circular electrodes held together by a large force

(Fig. 6.5). Atthey (1974) gave grounds for assuming that only

the

joule

heating

Q

is

significant. As

the

electrodes are cooled, the expectation

that

the

highest temperature will occur

on

the

central plane, x = t, of

the

weld

specimen can

be

justified by

the

Maximum Principle before melting starts.

At

some time, t =

to,

the

central plane

CE

in Fig. 6.5 will reach

the

melting temperature U =

UM.

An

amount

of

heat

pLS 8x

is

required

to

melt a small element t - 8x

~

x

~

t,

where S is

the

area

of

the electrode.

The

joule

rate

of heating

of

the

element

is

OS 8x and no

other

heat

can

enter

the element since no

other

part

of the sheets can

be

at

a higher

temperature than

that

at x = t.

The

only possibility is

that

the

element

t-8x~x~t

remains at the melting temperature for a time Lp/Q.

During this time, other parts of

the

sheets will reach the melting tempera-

ture

so

that

during the time interval

to~t"'"'to+Lp/Q

there will

be

a

region,

t'(t)~x"'"'t

say, which is

at

the melting temperature and

is

neither fully molten nor fully solid. This

is

half

the

mushy region existing

between the solidus and liquidus boundaries

if

the sheets are of equal

thickness.

The

one-dimensional heat-conduction problem for a material with

constant heat capacity C

=

cp

can

be

expressed by

the

equation

K;Pu

+Q=aH

(6.61)

ax

2

at

Enthalpy method

241

where u =

u(H)

is

defined by

u=H/C,

H~CuM'

}

u = u

M

,

CuM<H

<

CuM

+ Lp, (6.62)

u=(H-L)/C,

H~CuM+Lp.

The

body-heating

term

Q(u)

is

taken

to

be a given piecewise linear

function of temperature only and other boundary conditions are, for

example,

au/ax

=au,

x=O; au/ax

=0,

x=t.

(6.63)

An

initial condition

H(x,

0) = ho(x)

is

given. Atthey (1974) approximated

(6.61) by the explicit finite-difference scheme

(6.64)

where..\

= 8t/(8x)2 and

the

conditions (6.63) become, as in (6.22), (6.23),

uo=

u~(2-a

8x)/(2+a

8x), (6.65)

where E

8x

= t. The initial condition

is

simply

H:!.

= ho(m 8x). Proceeding

as

in

§§6.2.1, 2, Atthey (1974) showed that the finite-difference solution

converges

to

a unique weak solution analogous

to

(6.13) modified to

include

the

body-heating term and

the

derivative boundary conditions

(6.63).

Figure 6.6 shows a typical picture of the solid, mushy, and liquid

regions from a computed solution (Atthey 1974).

"

S

1.0

.......... -*.* •••• *

•••••••

*.****.*

••••

............ *

••

_._

••••

-

.......

-

••••••••

............ *.*****

•••

******** *

••

* •• -

••

..............

.._

••••

*

•••••••

* •• *

.......

.

.............. • *

.......

_

•••

-."'

••

-

•••••••

..............

..

•••• -••••

_*

..............

..

............

0..

•

._

•••••

* *.*.* *

........

*'

•

........... u...

..

............

_*

•••••••• _ •

..................

..............

**.........

.

....

Solid

..................

..*

...

"'

..........

"'._.-

................... .

............

-

..........

"'.

..................... *

........

**

••••••••••

...................... **

••••

*

••••

*

••

*.**.

.......................

..**

••

**

••

*.**.***

..·.Liquid

No

symbol: Mushy

.............. .......... * ... *

..........

*.*.

........................ •

••

*.*

•••••

**

•••

......................... • ••• ****

••

"'*

•••

:;

0.8

"

N

~

S

o

z

.........................

.*

•••

*.**

••

*

........................... *.*."'*.* •

..

-.

.......................

..

................................

..................................

......................................

~

.......................................

.

....................................................

0.6

L-..

___

~:-::-

____

-:-

0.0 0.5

1.0

Normalized length

FIG. 6.6. Solid, mushy, and liquid regions

Crank J. Free and Moving Boundary Problems

Подождите немного. Документ загружается.