Crank J. Free and Moving Boundary Problems

12

Moving-boundary problems: formulation

and

appropriate initial conditions, where

fICD,

f2(T) are given fwlctions.

An

inverse problem would be to find ft(T),

MT)

such that a prescribed

motion

S(T)

is

produced.

The

automatic, real-time control problem

posed by this inverse situation is

of

practical importance, e.g., in steel

casting, and is elaborated by Hoffman and Sprekels (1982)

'Who

present

numerical solutions. A wider survey of the application of control techni-

ques

to

parabolic systems is given by Hoffmann and Niezgodka (1983).

1.3.6. Multi-phase problems

The

two-phase problem formulated in § 1.2.2 above can

be

easily

extended

to

more than two phases and moving interfaces. More equations

of type (1.7) and more Stefan conditions (1.9) together with appropriate

conditions

on

fixed boundaries and

at

t = 0 determine

U1>

U

2

,

•••

, Un+l

and

S1>

S2,

...

,5,..

The

essential feature of a multi-phase problem

is

that

each domain and

the

solution of

the

corresponding parabolic equation is

connected

to

every neighbouring domain and solution through a set

of

- relations expressing

the

physics

or

chemistry of the problem being consi-

dered, e.g. the Stefan condition. A simple example is provided by a

collection of ice cubes in a glass

of

wa~er.

There is one heat-flow equation

in

the

water phase and one in each ice cube.

In

the

most general case

the

'cubes' have different

heat

parameters, and equations and solutions in

each one are linked with

the

water-domain equation and solution by

Stefan conditions on each cube-water, interface. Cannon (1978) relates

the

analysis of multi-phase problems to a problem in which two sub-

stances in solution diffuse

and

react quickly and completely on a moving

boundary.

The

ablation of

the

alloy walls of a space vehicle leads

to

a three-phase

problem with solid, liquid, and vapour phases and two moving boundaries

(Koh

et

al. 1969).

Bonnerot and Jamet (1981) discuss a simple, one-dimensional problem

involving three phases, solid, liquid, and vapour, which can appear

and

disappear. They consider a solid material which initially occupies

the

region 0 < X <

a,

where X is

the

space coordinate in

the

direction

perpendicular

to

the

wall.

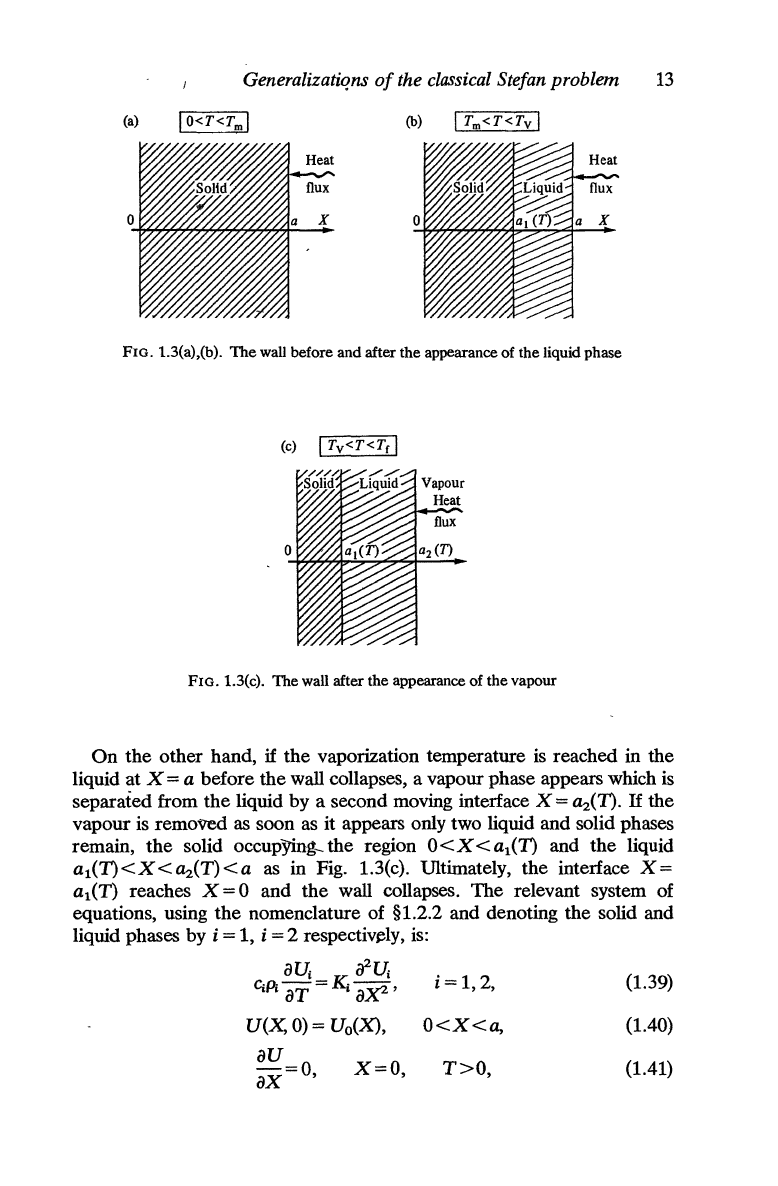
The

wall

is

at

a known temperature initially

and then it is heated from

the

right (Fig. 1.3(a) by a given heat flow on

X

=

a.

The

surface X = 0 is thermally insulated.

When

the

temperature

on

the

right side of the wall, X =

a,

reaches the

melting temperature a liquid phase appears. Assuming no density change

on melting,

the

solid occupies

the

space

O<X

< a 1(1') and

the

liquid is in

al(T)

<X<a,

where

X=al(T)

is

the

melting interface (Fig.1.3b). This

interface moves

to

the

left and temperature increases at any fixed point.

If

the

melting interface X = al(T) reaches the left side

of

the wall X = 0

at T = T

f

before

the

temperature on X = a reaches

the

vaporization

temperature, the solid phase disappears and

the

wall collapses.

Generalizatiqns

of

the classical Stefan problem

13

FIG. 1.3(a),(b).

The

wall before and after the appearance of the liquid phase

(c) I

Tv<T<Tr

I

o

FIG. 1.3(c).

The

wall after the appearance of

the

vapour

On

the

other hand,

if

the

vaporization temperature

is

reached in the

liquid

at

X = a before

the

wall collapses, a vapour phase appears which

is

separated from

the

liquid by a second moving interface X =

aiT).

If

the

vapour

is

remowd

as

soon as it appears only two liquid and solid phases

remain,

the

solid occupymg_

the

region

O<X

<al(T)

and

the

liquid

al(T)<X<a2(T)<a

as

in Fig. 1.3(c). Ultimately,

the

interface

X==

al

(T) reaches X = 0 and

the

wall collapses.

The

relevant system of

equations, using

the

nomenclature of § 1.2.2 and denoting

the

solid and

liquid phases by

i = 1, i

==

2

respectiv~ly,

is:

au;

~u;

C;P;

aT

=

~

a~

,

i=

1,2,

(1.39)

U(X,

0)

= Uo(X),

O<X<a,

(1.40)

au=o

ax

'

x==o,

T>O,

(1.41)

14

Moving-bf!undary problems: formulation

au

Kl

aX

=

F(T),

X=a,

(1.42)

au

K2

aX

=

F(T),

X=a,

(1.43)

U=U

m

, }

K

aU

1

_

K

aU

2

=L

dal

1

aX

2

ax

mP

dT'

(1.44)

U=U

v

,

aU

2

da2

K2

ax-F(T)=Lvp

dT'

}

x~a,(T).

(1.45)

(1.46)

Here

L

m

,

Lv

are latent heats of melting and vaporization respectively.

Numerical methods used by Bonnerot and Jamet are discussed in §4.3.3.

Tayler (1975) discusses the degeneration of phases

in

a slightly more

general way.

1.3.7. Simultaneous diffusion and heat

flow:

alloys

Alloy solidification problems differ from classical Stefan problems in

that

the

melting temperature is not known in advance; it depends on

the

composition

of

the alloy. Typically, an alloy

is

considered

to

comprise a

pure substance containing a small concentration of one

or

more secon-

dary substances, conveniently referred

to

as

'impurities'.

The

solidifica-

tion of an alloy calls for a simultaneous study of the processes of heat

flow

and

the

diffusion of impurities.

An

introduction

to

the

essential ther-

modynamics can conveniently be based on

the

eutectic diagram for one

impurity shown

in

Fig. 1.4.

~~~------

____________

~

__

c

FIG. 1.4. Eutectic diagram

Generalizations

of

the classical Stefan problem

15

H at any point in

the

alloy the concentration of impurity

is

CA

and the

temperature

is

U represented by

the

point A in Fig. 1.4 this point

is

in the

solid region.

H the concentration is increased

to

a value CB at the same

temperature, the point

B

is

reached in the liquid region. Equilibrium

between

the

impurity and

the

pure alloy

is

not possible in

the

range

Cs < C <

Cv

This

is

a region of instability

but

liquid and solid phases can

coexist in equilibrium

at

the

same temperature u with respective concent-

rations

cs(u) and

cdu),

e.g.

at

points

X.

Y in Fig. 1.4. Thus, the melting

temperature will depend

on

the

concentration of the impurity and

at

a

phase-change boundary there

will

_be

a discontinuous change in the

concentration related

to

the

melting temperature through the eutectic

diagram, i.e.

CL(U)-CS(u) for a

temp~ture

u.

A simple two-phase alloy soli9ification process can now

be

expressed in

non-dimensional terms as follows, where

Uh

Ch

Kl

refer,

to

the solid

phase and

U2,

etc.

to

the

liquid phase.

aUl a

2

Ul

aCl_

D a

2

Cl

;;t=Kl

ax2'

at

- 1

ax

2

'

aUz

a

2

u

2

aC2_ D a

2

C2

;;t=K2

ax2'

at

- 2

ax

2

'

aU2_

aUl_

ds

'Y2

ax

'Yl

ax

-

dt'

O<x<s(t),

s(t)<x

< 1,

aC2

aCl

ds

x =

s(t),

{32

a;-

{3l

a;=

(Cl - cz)

dt'

Ul

= U

2

=

g,

Cl

= cs(g),

C2

= CL(g),

(1.47)

(1.48)

(1.49)

together with appropriate conditions on

x

=0,

1 and t = 0. Tayler (1975)

discusses some special limiting cases of the general formulation. Fix

(1978) outlines a simplified model of alloy solidification due to Langer

and Turski (1977)

to

illustrate ideas

of

non-iinear instabilities associated

with Mullins and Sekerka (1963,1964) on the melting front and related

to

the

growth of dendrites in multi-dimensional problems.

The

simplifica-

tions in

the

Langer model are: (a) heat conductivity

is

everywhere

infinitely large; (b)

the

diffusion coefficient for the impurity

is

constant;

and

(c)

the

concentration

jump

CL(U,j-CS(U,j

is constant, independent

of

the

melting temperature. Fix then develops an alternative weak varia-

tional formulation of

the

complete alloy solidification problem. Ockendon

(1978) also derived a weak formulation in

one

space dimension. An

enthalpy formulation of alloy solidification and some solutions are pre-

sented in §6.2.7(ii).

Other examples of simultaneous diffusion and heat

flow

have been

16

Moving-boundary problems: formulation

examined by Mikhailov (1975,1976) and in flame studies by Crowley

(1980, 1981) and Buckmaster (1979) (see §6.2.7(iii)).

1.3.8.

Muskat's

problem

A problem that only involves fluid

flow

but

which is otherwise akin

to

the

alloy solidification problem in that

the

concentration on

the

moving

boundary

is

not explicitly specified

is

usually referred

to

as

the

Muskat

problem (1934,1937).

The

theory

is

that when two immiscible

fl~ds

in a

porous medium are in contact with each other, the movement of

the

interface formed and of

the

fluids constitutes a moving boundary prob-

lem. A typical system of equations given by Cannon (1978)

to

determine

the

pressures Pt(x, t), i = 1, 2, in

the

two media 1 and 2 is:

i=

1, 2,

(1.50a)

where

i=1

refers

to

O<x<s(t),

i=2

to

s(t)<x<l,

and O<t~T in

both cases;

PI(S(t), t) = P2(S(t),

t)}

al

apI/aX

=

a2

ap2/aX,

x = s(t),

#(t)

=

-al

apI/aX

(1.50b)

where

a;

are given functions

of

x,

Pb

and

</>{s(t),

p(s(t), t)} is known,

together with specified initial values of

Pb

i = 1, 2, at t = 0,

PI(O,

t) and

pil,

t) given functions of time,

and

s(O)

=

So,

0 <

So

< 1. Muskat's general

problem

is

not pursued further in this

book

but a particular case of

the

motion of two immiscible fluids

is

considered in §2.12.1 in relation

to

the

flow in a Hele-Shaw cell.

1.3.9.

Two and three space dimensions

As an example of

the

extension of

the

various one-dimensional prob-

lems formulated above in §1.2 and §1.3, the two-phase moving-boundary

problem with heat generation in each phase and on

the

moving boundary

can

be

expressed as follows, with x

the

space coordinate vector:

au

pc-=V(KVu)+Q,

at

au;

-;;--hu;

= gt(x, t),

. un

i=

1, 2,

O<t<T,

(1.51)

O<t<T,

(1.52)

(1.53)

Generalizations

of

the

classical

Stefan

problem

17

FIG. 1.5. Two-phase region with a moving boundary f(x, t) =

O.

and

[

au]2

aU2

aUI

K-

=K

2

--K

1

-=-pLv,.+q

an

I

an

on

the

moving boundary f(x, t} = 0, 0 < t <

T,

u(x,

O}

=

uo(x},}

t =

o.

f(x,

O}

=

fo(x),

(1.54)

(1.55)

With reference

to

Fig. 1.5, D =

DI

U D

2

,

aD

=

aD

I

U

aD

2

denote the

interior and boundary of the relevant domain.

The

operator V encompas-

ses different coordinate systems, e.g. rectangular, cartesian, cylindrical

and spherical polar, and generalized curvilinear.

In

heat conduction

nomenclature

Uj denotes

the

temperature in each phase, i = 1, 2, U

m

the

phase-change temperature, L

the

latent heat, n

the

outward normal

to

the

moving boundary f(x, t) = 0, and

v"

the velocity of this boundary

along

the

normal.

The

thermal properties

c,

p,

K and

the

heat generation

terms

Q,

q may

be

functions of

u,

x, and t and may

be

different in

the

two

phases,

Patel (1968) expressed

the

condition (1.54)

on

the

moving boundary in

the

more usable form

{

(

as)2 (as)2}

I

auI

2

as

1+

- + -

K-

=-pL-

z:;s(x

y

t)

ax

ay

az

I

at'

, ,

(1.56)

for

the

case q =

O.

This relationship connects explicitly

au/az

with deriva-

tives'"'

of

the

moving-boundary surface f(x,

t}

= 0 written as z = s(x,

y,

t}.

Similar relations hold for

the

other two components

au/ax

and

au/ay.

Patel's derivation of (1.56) for q = 0 is as follows, denoting temperatures

by

Uj, i = 1, 2,

and

considering the three-dimensional case in which the

18 Moving-boundary problems: formulation

moving boundary is given by f(x,

y,

z, t) = 0. Thus we have

u;(x,

y,

z, t) =

Urn,

i = 1, 2,

(1.56a)

K

aUI_

K

au

2

=

!Lv

I

an

2

an

p

'"

(1. 56b)

on

f(x,

y,

z, t) = 0, (1.56c)

where n is

the

outward normal and

Vn

the

normal velocity.

Then

n =

Vl/IVfl

=

VU;/IVu;I,

au;

-=Vu;

'n=(Vu;

• Vf)/IVfl =

IVu;1

an

'

v,.

=v

'n=(v'

Vf)/IVfI =

(v'

Vu;)/IVu;I.

Remembering from (1.56c)

that

df=

af dx+ af

dy+

af

dz+

af dt=O,

ax

ay

az

at

and hence

that

. af . af . af af °

x-+y-+z-+-=

,

ax

ay

az

at

we

see

from (1.56f)

that

IVfl

(

'

.•.

k·)(·af+.af+ka

f

) af

v,.=IX+JY+

z

1-)-

-

=--,

,

ax

ay

az

at

and

s~ilarly

for

IV

U;

I

v'"

so

that

Vn

= -(aflat)/IVfI =

-(aU;/at)/lvu;l.

Using (1.56e,g),

eqn

(1.56b) becomes

KIVUI

.

Vf-K

2

VU

2

' Vf=-pL(aflat),

and

by

differentiating (1.56a), (1.56c) we find

..

aU;

aflax

au; au;

aflayau;

ax

= aflaz

az

'

ay

=

afliJz

az

'

and hence by substituting (1.56i) into (1.56h)

[

1+faflax)2+(aflay)2][K aUI_K aU2]=_!L

aflat

\aflaz

aflaz

1

az

2

az

P aflaz'

(1.56d)

(1.56e)

(1.56f)

(1.56g)

(1.56h)

(1.56i)

(1.56j)

which is

the

same as (1.56) above for f(x,

y,

z,

t)

= z -

sex,

y,

t)

= 0.

For

Generalizations

of

the classical Stefan problem

19

q

1=

0 in (1.54) Patel derives

the

additional tenn

{

la/lax)

(a/lay)

}

-

VJ/laz

llx

+

a/laz

qy

+ 4:

on

the

right-hand side of (1.56j). Crank and Gupta (1975) derive the

two-dimensional single-phase

fonn

of (1.56)

by

a simpler argument.

By

combining (1.56e) with (1.56f), equation (1.S6b) can

be

written in the

form quoted by Carslaw and Jaegar (1959, p. 284)

(1.56k)

1.3.10. Implicit boundary conditions: oxygen diffusion problem

A feature common to all the problems fonnulated above in §§1.2 and

1.3 is that

the

Stefan condition and its generalizations connect the

position

or

velocity

of

the

boundary with the dependent variable u

or

its

derivatives, e.g. with

the

temperature gradient

aulax

on

the

boundary in

the

one-dimensional case. Problems exist, however, in which such an

explicit relationship does' not occur and Sackett (1971) introduced the

tenn

'implicit free-boundary problems'

to

describe them. They corres-

pond

to

the

special case L

=0

in (1.12).

A much-quoted example of an implicit condition

,-,ccurs

in

the

oxygen

diffusion problem. Practical details are given by Crank and Gupta

(1972a,b) and by Constable and Evans (1975,1976). First, oxygen

is

allowed

to

diffuse into a medium which absorbs and immobilizes oxygen

at

a constant rate.

The

concentration of oxygen

at

the surface of the

medium

is

maintained constant. A moving boundary marks the innennost

limit of oxygen penetration. This first phase of

the

problem continues

until a steady state

is

reached in which the oxygen does not penetrate any

further into the medium.

The

surface of the medium

is

then sealed so that

no

further oxygen passes in

or

out.

The

medium continues

to

absorb the

available oxygen already diffusing in it and, as a consequence,

the

boundary marking the depth of penetration in

the

steady state recedes

towards

the

sealed surface.

The

major problem

is

that of tracing this

movement of the boundary and of detennining

the

distribution of oxygen

as a function of time. A secondary problem in

the

application of numeri-

cal techniques

is

associated with

the

discontinuity in

the

derivative

boundary condition which results from the abrupt sealing of the outer

surface.

If

C(X,

1)

denotes the concentration of oxygen free to diffuse

at

a

distance X from

the

outer surface of

the

medium

at

time

T,

D

is

a

constant diffusion coefficient, and

m,

the rate

of

consumption of oxygen

per

unit volume of

the

medium,

is

also assumed constant for C(X,

1)

> 0,

20

Moving-boundary problems: formulation

the steady state

is

defined by a solution of

d

2

C

D

dXZ-m=O

which satisfies

the

conditions

c=ac/ax=o,

where

Xo

is

the

innermost extent of oxygen penetration, and on

the

outer

surface

c =

Co

= constant, X = 0.

The

required solution

is

readily seen

to

be

given by

After

the

surface X = ° has been sealed,

the

position of the receding

boundary is denoted by,Xo(T) and the problem

to

be solved becomes

aC

a

2

c

aT=D

aXZ-:

m

, O.,;;X.,;;Xo(T),

(1.57a)

aC

=0

X=O,

T;-;.O,

ax

'

(1.58a)

aC

C= ax=o,

X=Xo(T),

T;-;.O,

(1.59a)

m '

C=_(X_X)2

2D

0 ,

T=O,

(1.60a)

where T = °

is

the

moment when the surface

is

sealed. By making

the

changes of variables,

X

x=-

Xo'

D C

c=--=-

~

2C

o

'

and denoting by s(t)

the

value of x corresponding to Xo(T),

the

above

system

is

reduced

to

the

following non-dimensional form:

ac

= a

2

c_

1

at ax

2

'

O,,;;x";;s(t),

(1.57)

ac=o

ax '

x=o,

t;-;.o,

(1.58)

c

=ac/ax=o,

x

=5

s(t),

t;-;.o,

(1.59)

c=t(1-X)2,

O.,;;x.,;;1,

t=o,

(1.60)

Generalizations

of

the classical Stefan problem

21

where c is

the

concentration of oxygen free to diffuse.

It

is

the

absence of

as/at

in (1.59)

that

renders this problem implicit.

Schatz (1969) uses

the

transformations

w = au/ax

or

w=au/at

(1.61)

to

express

an

implicit problem in

an

explicit form. Thus, in

the

ablation

problem

of

§1.3.5 for

A';O

but

q'l=O

in (1.35)

the

use of w =

au/ax

gives

w=q(t),

O<x

<s(t),

aw

..

-=-qs+g

ax

'

aw

.

-=

[(t), x

=0,

t>O,

ax

x = s(t),

w=a4>/ax,

t=O,

O<x<1.

-<1.62)

If

q = 0

the

appropriate transformation is w = au/at provided

g'l=

0 and u

is differentiable at

t:;:

0, x = 0

and

1, which requires

[(0)

=

4>(0)

and

g(O)

=

4>(1),

q(O)

=

4>'(1).

Otherwise,

the

Schatz transformation introduces

singularities. Tayler (1975)

and

Ockendon (1975) use

the

oxygen diffu-

sion problem

to

illustrate these statements. Thus for A = 0, g =

t,

q = 0,

and

au/ax = 0

on

x = 0,

use

of

the

transfonnation w = au/at would

be

straightforward. However,

the

initial condition (1.60) used by

Crank

and

Gupta

(1972a) coupled with (1.58) means that c is

not

differentiable

at

x = 0, t =

O.

The

Schatz substitution, w =

ac/at,

reduces

the

system

(1.57-

60)

to

ifw/ax

2

=

aw/at,

O<x<s(t),

1

w =

0,

aw/ax = -ds/dt, x = s(t),

(1.63)

w=O,

s=l,

t=O,

aw/ax

= 8(t), x = 0,

where

8(t) expresses

the

discontinuous jump in

ac/ax

from

-1

to

zero

given

by

(1.60)

and

(1.58)

at

x =

0,

t =

O.

Proofs

that

the

transformations will convert

an

implicit problem into an

explicit

one

and

vice versa together with

an

examination

of

the

necessary

conditions

are

given

by

Schatz (1969). ,

Various methods

of

obtaining numerical solutions

of

equations (1.57-

60)

are

described in §§3.5.2, 4.2, 4.3.1-3, 5.1, 6.2.7(i), 6.3, 6.4.1, and

6.4.2. Results

are

presented in Tables 3.1,

3.2,4.1,4.2,6.3,

and

6.6-8.

A two-dimensional version of

the

oxygen diffusion problem (Evans and

Gourlay 1977) is

referred

to

in

§6.3.

Crank J. Free and Moving Boundary Problems

Подождите немного. Документ загружается.