Crank J. Free and Moving Boundary Problems

52

Free-boundary prohh!lIIs: fiJl'll/lIlatio/l

. Comincioli (1975) proposed this formulation, established mathematical

properties, and gave the following

SOR

scheme for a numerical solution.

Starting with an arbitrary vector

{w~~?\},

where

q(O)

is

a first estimate

of

q,

a sequence of vectors

{w~~J)}

is

generated and subsequently

q(r)

and

{w~~.~}

from the equations

i = 1, 2,

...

,n.

(2.69g)

An

outer

iteration for

q(r)

is

built into the algorithm

as

described in

§8.5.1. Thus a non-linear equation

is

to

be

solved for

w~~.~f)

for each i

and

r,

but the solution can

be

given explicitly because of the definition of

H.

The

problem has become

one

of finding

w~"i.~f)

which minimizes

the

function

F(t)

=!~it2+wt+-

[w/;

+(1-W)~iW~~J.i-W

if

~jW~~'~ji)

j=l

- W jll

~jW~"i.\,j]t,

(2.69h)

where t+=!(t+ltl}. This formulation could

be

used in the other problems

of this chapter.

2.3.7. Arbitrary-shaped

dam

Baiocchi (1975a) formulated the problem of porous flow through a

dam with an arbitrary shape and

an

impermeable horizontal base separat-

ing two reservoirs using

the

quasi-variational inequalities introduced by

Bensoussan and Lions (1973).

The

cross-section of

the

dam

(Fig. 2.7) has

the form

D(x,

y) with 0 < x <

Xl>

0 < Y <

Y(x),

where Y is a smooth

y

FIG. 2.7. Arbitrary-shaped

dam

Other two-dimensional dams

53

concave function of x in 0 < x <

Xl

and, with reference

to

Fig. 2.7,

Y(XF)

=

Yb

Y(Xd

=

Y2

are the heights of the two reservoirs respectively.

The flow region

n

is

defined by ABDF, an extended variable

4>

is

defined

as

4>

=

4J

in

nand

4>

= Y in D -

n,

and the Baiocchi transformation

defines

z(x,

y)

by

z(X,y)=

f('l'J-4J)d'l'J

inD,

As before

V2z=1

in n and

~z=O

in

D-O,

so that

0~V2z~1

in D.

The conditions for

z(x,

y)

are

z(x, y);a.z(x, Y(x)),

O~y~Y(X),

(2.70a)

z=O

onAB,

Zy

= y -

Y2

on BC,

Zy

= Y -

Yl

on AF,

Zy

=0

on

FEC,

and

z(x,

Y(x))

is concave as a function of X in

XF~X~XC.

Also

q

= zx(x, Y(x)),

(2.70b)

(2.70c)

(2.70d)

(2.70e)

The

variational statement obtained by Baiocchi (1975a) for the functions

z(x,

Y),

using test functions v(x,

y)

which are square summable

on

D

together with their first derivatives, and with v(x,

y)

= 0 on AB,. is written

as

a(z, v -

z)+

j(z, v);a. j(z,

z)+(v-

z)

(2.71)

where

D

-Yxxzy(v-z)}dxdy,

(2.71a)

(v-z)=-

f f

(v-z)dx

dy+

fF(l+

Y;)(Y(X)-Yl)

x{v(X,

Y(x))-z(x,

Y(x))}dx

+

fl(1+

Y~){Y(x)-yJ{v(x,

Y(x))-z(x,

Y(x))}dx,

Xc

(2.71b)

j(z,

v)

= f f

[v

(x,

y)

- z(x, Y(x))]+

dx

dy,

(2.71c)

D,

j(z, z) = f f[Z(x,

y)-

z(x, Y(x))]+ dx dy,

(2.71d)

54

Free-boundary problems: formulation

where the domains

Db

D

2

,

D3 are the parts of D between 0 < x

::s:;

XF,

XC::S:;X<Xb

XF<X<XC

respectively and in (2.71c) and (2.71d),

[t]+=

t for

t~O,

[tJ+

= 0 for

t::s:;O.

The

tenn

'quasi-variational inequality' is used in

this fonnulation because

the

function z(x,

Y(x))

depends itself on the

unknown function

z.

Baiocchi (1975a) gave a derivation of (2.71) which was reproduced by

Bruch (1980). Baiocchi

(1975a,1975b), Baiocchi, Comincioli, and

Maione (1975), and Comincioli (1975) established

the

existence of maxi-

mal and minimal solutions for a range of problems, and Comincioli

(1975) and Baiocchi

(1975a) gave numerical algorithms

to

obtain approx-

imations

to

them. Uniqueness

of

the

solutions of their quasi-variational

inequalities

is

conjectured because

the

numerical experiments showed the

maximal and minimal solutions

to

be

the same (Baiocchi 1975c; Gilardi

1976; Baiocchi, Brezzi, and Comincioli 1976).

The

problem of

the

dam

with slanting inlet face §2.3.4

is

the

special

case

Xc

=

Xl

= Xe (Fig. 2.7) of (2.71) and was solved in this way by

Baiocchi

(1975a) and Comincioli (1975) who gave algorithms and numer-

ical results for

the

maximal and minimal solutions. Bruch (1980) indicated

how the quasi fonnulation can

be

reduced

to

the fonnulation given above

in §2.3.4 when

Yx(x) =

Yl/XF'

Baiocchi (1975a) showed how

the

varia-

tional inequality (2.36) for

the

simple

dam"

problem

is

regained from

the

general quasi theory when D is a rectangle.

The

dam

with vertical inlet face and horizontal base

but

slanting exit

face also presents a quasi-variational problem.

In

Baiocchi et

al.

(1976)

and Baiocchi and Magenes (1974, 1975)

the

problem is expressed as a

family of variational inequalities depending

on

two parameters q and

the

horizontal distance

to

the

intersection of

the

free surface with

the

seepage

face. Baiocchi

et

al.

(1975) solved a quasi-variational inequality for

the

dam with both

faGes

slanted

on

a horizontal base.

In

§§2.11

and

8.6 generalized fonnulations are given of problems in

arbitrary shaped dams by Brezis

et

al.

and independently by

Alt

who

constructed a general purpose algorithm.

Various aspects of steady flow in a fairly general region, leading

to

a

truncation algorithm (§6.3), were studied by Rogers (1980, pp. 333-82).

2.3.8. Arbitrary-shaped dam with

toe

drain: split-domain method

In

order

to

avoid the complexities of quasi-variational inequalities

Bruch

et

al.

(1982) proposed

to

use

the

Baiocchi transfonnation and

fonnulation only in

the

part

of

the

solution domain containing

the

free

surface, and in

the

remaining

part

of the domain

to

apply classical

methods for solving fixed boundary-value problems.

The

two regions thus

defined have

an

overlap which permits an alternating iterative numerical

scheme

to

be

adopted.

The

approach was first used by

Remar

et

al.

Other two-dimensional dams

55

y

FIG. 2.8. Split-domain method

(1982) (see §8.5.2) and was applied to the arbitrary-shaped dam with toe

drain by

Bmch

et al. (1982).

With reference to Fig. 2.8 the

flow

domain 0

is

the region AFCBA

defined by

O<XO:;;XF,

O<yO:;;Y(x);

xF<x<Xc,

O<y<f(x),

where

y=

f(x)

is

the

free surface and f(xp) = Y

F

,

f(xc;) = 0, df(xF)/dx =

-1/YAx

F

),

df/dx =

-00

at x = xc.

The

solution region 0 is extended

to

the known region

D,

O<xo:;;x

F

,

0<

y <

Y(x);

XF

< X <

xc,

0 < y <

YF,

i.e.

AFEC.

The problem could

be

formulated in terms

of

the

velocity potential

<fJ

and stream function

1/1

or

in terms of the Baiocchi variable w(x, y) with equations similar to those

for

the

rectangular

dam

with toe drain in §2.3.L

Instead,

Bmch

et al. (1982) split

the

domain D into two regions,

D4>

and D

w

,

with a common overlap where

D4>

is

defined

to

be

the region

O<XO:;;XF,

O<y<Y(x);

xp<x<g(y),

O<Y<YF, where

x=g(y)

is the

equation of the chosen curve

'Y

between F and

Fl

in Fig. 2.8. This leaves

Dw

which is

the

rectangular region

FECF~,

XF<X<XC,

O<Y<YF and

finally

Or

.•.

is

the region

xF<x<xc,

O<y<f(x).

The fixed boundary-

value problem in

D4>

is

V

2

<fJ

= 0 in

D4>

(2.72)

<fJ

= yp

on

AF,

<fJ

= Y -

Wy

on

'Y

</Jy

=0

on

AFt>

O<X<XF

t

'

(2.72a)

(2.72b)

In

Dw

the problem in terms of the Baiocchi variable w(x, y) given by

(2.20)

or

(2.46)

is

~w

=0

in D-Or.s.

wy=O

on

BC,

XB<X<XC,

(2.73a)

(2.73b)

(2.73c)

56

I';Y'('-/Jo/lfl(/""v {J1'O"'l'IIIS: formulation

w=

f'(<p-1/)d1/

on

FF~,

y

w

=0

in

DW-O

f

.

s

.

w;;:OO

in D

w

,

w>O

in

fit.s.

Thus in

Dw

we have the differential inequalities

w(x,

y);;:OO,

I-V

2

w(x,

y);;:OO,

and

The

associated variational inequality

is

(2.73d)

(2.73e)

(2.73f)

w(I-~w)=O.

(2.73g)

JJV(V-W).VWdXdY;;:O-

JJ(V-W)dXdY,

(2.74)

Dw

where v agrees with w

on

F~B

and

FF~,

v = 0

on

FE

and

Ee,

and

v;;:Oa.e.

on

Dw.

Bruch and Sloss (1981) used (2.74)

to

show the uniqueness

and

existence of

the

solution w(x, y).

This is another problem in which

the

flow rate q is unknown and

the

necessary compatability condition similar

to

that used by Sloss

and

Bruch

(1978)

is

(2.75)

The

essential feature of the split domain is that information

is

inter-

changed between

the

two domains along

the

line

FF~

and

the

curve

'Y.

The

solution of (2.73)

or

(2.74) in

Dw

provides values of w

to

be

used in

the derivative boundary condition (2.72a)

On

'Y

in

Dot>;

and correspond-

ingly the solution of the equations (2.72) yields values of

<p

to

be

used in

the boundary condition (2.73d) in

Dw.

Bruch, Sloss,

and

Remar

(1982) applied their split-field approach

to

the

particular example in which Y

F

= 30 ft, X

F

= 30 ft,

XB

= 60 ft. They

took

q(O)

= 15

fe/sec

per

foot depth normal

to

the

plane of flow

and

q(l)

=

16fe/sec

per

foot depth.

An

alternating method was used in which an

SOR

scheme was applied

to

a triangular finite-element mesh with linear

shape functions in

the

Dot>

region coupled with a finite-difference

SOR

scheme with projection in

the

Dw

region.

The

relaxation parameter was

1.85.

For

each value of

q,

discretized solutions of (2.72-72b) for

<p

and

(2.73a-f) for w are subjected

to

the

compatability condition (2.75), using

the

secant method (see equation (8.92».

The

alternating method between

solutions in

Dw

and

Dot>

was similar

to

that described by

Remar

et

al.

(1982). Bruch et

al.

(1982) gave computational and iteration information

for two grid sizes

Ax

=

Ay

= 2.5 ft and

Ax

=

Ay

= 1.0 ft.

In

a comparison

with earlier results obtained by solving for w throughout the whole

domain (Sloss

and

Bruch 1978),

the

calculated position of

the

free

Three-dimensional dams

57

boundary

was found

to

be

the

same for

the

two methods with

I1x

=

l1y

=

2.5 ft.

With

I1x

=

l1y

= 1

ft

the

point

of

intersection C of

the

free surface

with

the

drain

was

the

only

point

of difference

and

the

split-field value

was

more

accurate

and

its computing time was shorter.

2.4. 'Three-dimensional

dams

The

formulation of problems in three-dimensional dams introduces

no

essentially

new

features

that

do

not

occur in

the

two-dimensional prob-

lems.

The

differences

are

matters of complexity

rather

than

of principle.

When

the

Baiocchi transformation

and

method

are

to

be

used

the

a priori

unknown solution region is extended across

the

unknown free surface

into

a known domain which is

three

dimensional.

The

transformation

becomes

I

g(X,Y)

w(x,

y,

z)=

z

[<f>(x,

y,

l1)-l1]dl1,

(2.76)

where

z = g(x, y) is

the

free surface

and

cf>

is

the

modified velocity

potential (2.5). Stampacchia (1974) formulated a variational inequality

and

gave existence

and

uniqueness proofs. Gilardi (1977) expressed a

three-dimensional flow through

porous

media as a quasi-variational in-

equality

and

established an existence theorem.

Bruch

(1980) mentioned

other

theoretical

papers

by Caffarelli (1976)

and

by

Carbone

and

Valli

(1976, 1977), who considered a three-dimensional non-homogeneous

dam

with variable cross-section.

Stampacchia's (1974) formulation, reproduced

by

Caffrey

and

Bruch

(1979)

and

outlined below

for

the

dam

shown in Fig. 2.9, is

seen

to

be

closely similar

to

the

two-dimensional rectangular

dam

problem

formu-

lated

in

§§2.2.1

and

2.2.3.

The

width of

the

dam

between

the

impervious

sides is

denoted

by

a,

x =

4>1

(y) is

the

inlet face,

and

x = 4>iy)

the

outlet

FIG. 2.9. Three-dimensional flow

58

Free-boundary problems: formulation

face.

The

wetted parts of

the

inlet

and

outlet faces of

the

dam

are

denoted by

Flo

F

2

,

and

Fi

respectively, where

F

1

(x,

y,

z)

is defined by x =

<l>l(Y),

O~

Y

~a,

0

~z

~Zh

(2.77a)

Fix,y,z)

is

defined by X =

<l>2(Y),

O~y~a,

0~Z~Z2'

(2.77b)

and

Fi

by x = <l>iy),

O~y~a,

The

wetted sides

of

the

dam

are

denoted by

Sl

and

S2

where

SI(X,

y,

z)

is

defined by

<1>1(0)

~x

~2(0),

y = 0, 0

~z

~g(x,

0),

(2.78a)

and

y=a,

O~z~g(x,

a).

(2.78b)

The

flow region

11

is

defined by

<1>1

(y) < x <

<l>2(y),

0 < y <

a,

0 < z <

g(x, y),

and

g(I(y),

Y)=Zlo

g(2(Y),

Y)=Z2

as

in Fig. 2.9.

The

Baiocchi

variable w(x,

y,

z)

is

defined by (2.76) in

11

and

is zero

in

D-11,

where D

is

the

extended region of

the

dam

up

to

the

height

of

the

inlet reservoir

and

is

the

domain

<l>1(Y)<X<2(Y),

O<y<a,

O<Z<ZI.

The

problem is defined by

the

equations

V2q,

=0

in

11

q,=ZI

on

Flo

q,=Z2

on

F

2

,

q,=z

on

Pi,

q,z

=0

on

the

base B, <l>1(y)<x<iy),

O<y<a,

z=O,

</Jy

= 0

on

Slo

S2,

q,

= z,

aq,/an

= 0

on

the

surface z = g(x, y).

(2.79)

The

formulation in terms

of

w(x,

y,

z)

follows closely

the

reasoning of

§2.2.3 for

the

two-dimensional problem. Slightly

more

detail is given by

Caffrey

and

Bruch (1979). Thus starting from (2.76) we derive

I

g(X,Y)

aq,

Wx = - (x, y, 1j) d1j,

z

ax

J

g(x.y)

aq,

Wy = - (x,

y,

1j) d1j,

z

ay

W

z

=z-q,(x,

y,

z).

(2.80)

It

follows immediately

that

in D -

n,

Wx = Wy = W

z

= 0,

and

since W = 0 by

definition in D -

n,

so W

and

its first derivatives

are

continuous across

the

free surface.

Three-dimensional dams

59

The

second derivatives

of

W

are

i

g(X'Y)

if

d

dg

Wxx

= z

dX

2

[<f>(x,

y,

1])]d1] +

dX

[<f>(x,

y,

g(x,

y»]

dX'

d

W

zz

=

--

[<f>(x,

y,

z)]+

1,

dZ

i

g(X,Y){

d2

d

2

}

Wyy

= z -

d1]2

[<f>(x,

y,

1])]-

dX2

[cf>(x,

y,1])

dTl

d

dg

+ dy

[<f>(x,

y,

g(x,

y»]

dy ,

(2.81)

where

the

equation

V

2

<f>

= 0

has

been

used

to

obtain w

yy

•

Furthennore,

J

g(x,y)

d

2

d d

z

d1]2

[<f>(x,

y,

-ri)]

d1]

=

dZ

[<f>(x,

y,

g)]-

dZ

[<f>(x,

y,

Z)],

so

that

finally, by expanding

the

condition

d<f>ldn

= 0

on

Z = g(x, y) in

tenns

of

its components

d<f>ldX,

dgldX,

etc., we

have

~W=O

in

D-G.

(2.82)

The

boundary

conditions

for

w

on

the

sides

of

n follow readily by

combining appropriate items in (2.79)

and

(2.80)

and

are

listed in (2.85)

below.

The

condition for w

on

the

base B of the dam, defined in (2.79), is

less obvious.

We

know

that

in

n,

<f>

satisfies

the

weak

fonn

of

V

2

<f>

= 0, so

that

J J

J{

d<f>

dV

+

d<f>

dV

+

d<f>

dV} dx

dy

dz

= 0

dX

dy

dZ

(2.83)

for all functions

v(x,

y,

z)

with continuous derivatives in n

and

which

are

zero

near

the

faces

Flo

F

2

,

and

Pi.

Confining attention

to

the

base B of n

by

choosing v(x,

y,

z)

= vo(x, y), where

Vo

has continuous derivatives in B

and

vanishes

on

the

curves x =

<Ill

(y), x = <Iliy),

0:;;;;

y

:;;;;

a,

(2.83) reduces

to

J J

{

dVO

J

g(x,y)

d<f>

dVo

1

9

(X,Y)

d<f>

}

-

-d1]+-

-d1]

dxdy=O

dX

0

dX

dy dy

,

B

which after using (2.80) becomes

J J

{

dVO

dWo

+

dVo

dWO}

dx

dy

= 0,

dX dX

dy

(2.84)

B

where wo(x, y) = w(x,

y,

0) in B.

60

Free-boundary problems: formulation

The complete formulation in terms of w derived by Stampacchia (1974)

is

therefore

V2w=1

inn,

w;a:O

in

D,

W=!(Zl-Z)2

V2W=0 in

D-O,

w=O

in

D-.o,

w = 0

on

F;,

Wy

= 0

on

Sh

S2,

W;""

+

Wyy

= 0

on

B.

(2.85a)

(2.85b)

(2.85c)

(2.85d)

(2.85e)

The

boundary conditions for the solution of (2.85e) are

Wy

= 0

on

(x, 0, 0)

and on

(x, a,O) together with w(<pl(y),

y,

0)

=!zf

and

w(<p

2

(y),

y,

0)

=!z~.

Conditions (2.85a), (2.85b) can

be

expressed

as

the inequalities

w;a:O,

1-V

2

w;a:0,

w(l-~w)=O

inDo (2. 85f)

Stampacchia (1974) established

the

equivalent variational inequality for

w which takes

the

usual form

J J

Jvw.

V(v-w)

dx dy dz;a: - J J

J(V-W)dX

dy

dz

(2.86)

D D

for all functions v(x,

y,

z)

satisfying the usual conditions for such test

functions and where

v vanishes near the boundaries of D apart from Sl

and

S2'

The

proof follows closely

that

of (2.36) in §2.2.4. Stampacchia

established some of the mathematical properties of

W.

In

Chapter 8, §8.5.1(ii) contains two numerical algorithms and a

graphical solution for two different three-dimensional dam problems (see

Figs. 8.15, 8.16(a) and (b». Caffrey and Bruch (1980) treat

the

same

dam

with a toe drain.

2.5. Coastal aquifer

The

extraction of fresh water by means of a well from a layer of porous

rock

or

soil jutting out into

the

sea is of practical importance.

The

situation in such

an

aquifer, shown in Fig. 2.10(a), is that the upper

part

of the porous medium contains fresh water and sea water has penetrated

the lower part.

The

region from which fresh water can

be

extracted

without contamination by salt water

is

thus bounded below by

the

upper

surface of

the

entrapped sea water. The simplest problem, therefore,

is

to

determine the extent of

the

sea water in the absence of a well.

The

mathematical treatment of this problem presented by Baiocchi et

al. (1973a) is closely similar

to

that

for the simple rectangular

dam

in

§2.2.

The

known quantities are

Yl

=

AF,

the height above sea level of the

inlet fresh water, and the densities

Pf

and

Ps

of the fresh and salt water,

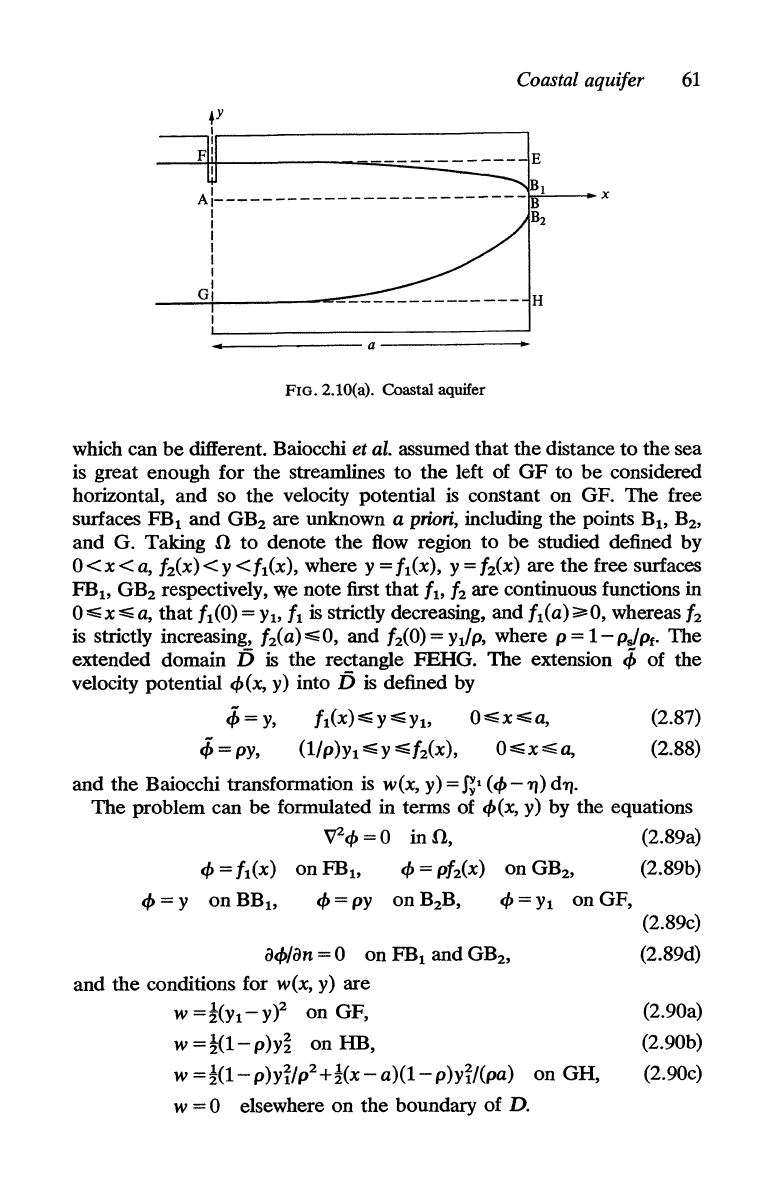
Coastal aquifer

61

-----------

E

J.n'-----x

--~~--------=-~-~-------------

H

••

-----------a------------

FIG.2.10(a). Coastal aquifer

which can

be

different. Baiocchi et

al.

assumed that the distance to the sea

is great enough for the streamlines to the left of

GF

to be considered

horizontal, and so the velocity potential

is

constant on GF. The free

surfaces

FBl

and GB

2

are unknown a priori, including the points

B1>

B

2

,

and G. Taking

n

to

denote

the

flow region

to

be

studied defined by

O<x<a,

f2(X)<Y <fleX), where Y = fleX), Y =

f2(X)

are

the

free surfaces

FB1>

GB

2

respectively, we note first that

f1>

f2

are continuous functions in

O..;x

";a,

that fl(O) =

Y1>

fl

is

strictly decreasing, and

fl(a)~O,

whereas

f2

is strictly increasing,

fia)

";0,

and f2(0) =

Yl/P,

where P =

1-

pJpf. The

extended domain

i5

is the rectangle FEHG. The extension

cb

of the

velocity potential

q,(x, y) into

i5

is

defined by

4>=y, fl(X)";Y";Y1>

O,,;x";a,

4>=PY,

(l/p)Yl,,;y..;f2(X),

O,,;x";a,

and the Baiocchi transformation

is

w(x, y) =

~1

(q,

-1)

d1).

(2.87)

(2.88)

The

problem can

be

formulated in terms of q,(x, y) by the equations

V2q,

= 0

in

n,

(2.89a)

q,

= fleX) on

FB1>

q,

=

pf2(X)

on GB

2

, (2. 89b)

q,

= Y on BB

1

,

q,

=

PY

on

B

2

B,

q,

=

Yl

on GF,

a<wan

= 0 on

FBl

and GB

2

,

and the conditions for

w(x, y) are

W=!(YI-y)2

onGF,

w=!(1-p)y~

on HB,

w

=!(1-p)yVp

2

+!(x-a)(1-p)yV(pa)

on GH,

w = 0 elsewhere on the boundary of D.

(2.89c)

(2. 89d)

(2.90a)

(2.90b)

(2.90c)

Crank J. Free and Moving Boundary Problems

Подождите немного. Документ загружается.