Crank J. Free and Moving Boundary Problems

42

Free-boundary problems: formulation

y

r

1---------.

l'

~A

-Q:-------i'::o::::~-X

~~~D~

FIG. 2.2.

Dam

with toe drain

the extended domain

O<X<XD,

O<Y<Yl

and

cI>(x,

y)

is

defined by

cI>(x,

y)=cP(x, y) _ in_f!} (2.48)

=y

in

D-n,

and

~(x,

y) by

~(X,

y) =

t{!(x,

y) in

f!

= 0 in

V-f!.

(2.49)

The fonnulations in tenns of

C/>,

t{!,

and w are given together for conveni-

ence. The problem

is

defined in the two ways as follows

v

2

c/>=0

or

cf>x

-1/1.;

= 0,

c/>y

+

t{!x

= 0

inn,

(2.S0a)

c/>

=

Yl>

w=~(Y-Yl?

onAF,

(2.S0b)

c/>=O

onBC,

wy=O

onBC,

(2.S0c)

c/>y

=0,

t{!

=

q,

w=h~-qx

onAB,

(2.S0d)

c/>

=

y,

oc/>Ion

= 0

or

t{!=0

onFC,

(2.S0e)

w=O

on

V -

f!

including

Fe.

(2.S0f)

The condition (2.S0c),

c/>

= 0 on BC, follows from (2.S) because it

is

usual

to

put p = 0 on the drain and Y = 0 there;

Wy

= 0 immediately from (2.22).

Furthermore,

wAx,

0)

=

Pol

c/>x(X,

'l'})

d'l'}

=

-q,

where q

is

the constant

flow

rate through all vertical sections of

the

dam in

n,

and so

the

condition for

w

On

AB (2.S0d) follows by integrating

Wx

with respect to x and ensuring

that

w(O,

0)

=

h~

to agree with (2.S0b) at Y =

O.

The variational inequality (2.36) is

to

be satisfied by w(x, y) for this

problem. Proofs of this and the uniqueness of the solution are similar to

those for the simple dam. Polubarinova-Kochina (1962) and

Harr

(1962)

Other two-dimensional dams

43

approximate

the

flow

rate

q for this problem

by

yi

(2.50g)

where t

=

AB

in Fig. 2.2, and this can be inserted as

the

known value of q

into

the

boundary condition (2.50d).

We

note

that

this implies

the

value

w(t,

0) = q2/6

at

the

point B, where

the

drain starts. Thus (2.50d) gives

w(t,O)=hi-qt

at

B while (2.50g) yields

Yi=~q2+2qt,

so

that

w(t,O)

becomes simply q2/6.

Bruch and Caffrey (1979) used both the finite-difference and finite-

element algorithms (8.90) and (8.91) to solve a typical problem. They

compared their results with

the

analytical solution (Harr 1962) for two

mesh sizes (see Fig. 8.17(a».

Before proceeding, it is convenient

to

comment

on

the

approximate

expression (2.50g) for

the

flow

rate

q.

It emerges as a special case in a

very lengthy treatment of

the

much more general problem of a trapezoi-

dal

dam

with a trapezoidal

toe

drain due

to

Numerov (1942) and

reproduced by

Harr

(1962, pp. 210-26). Sloss and Bruch (1978) give a

more direct derivation of

the

value

w(t,

0)

=~q2

based

on

Kozeny's

conformal transformation (1931). Its use in the present problem is strictly

an approximation because Kozeny's solution is for a

dam

with a parabolic

inlet face

and

a horizontal

toe

drain.

The

free surface is also found

to

be

parabolic

but

the

flow

pattern

near

the

toe drain is assumed

to

be

insensitive

to

the

geometry of

the

inlet face.

Kozeny's transformation from the

z = x + iy plane

to

the

w =

</>

+

il{!

plane, suitably adapted for

the

origin

at

A in the (x, y) plane (Fig. 2.2)

and

with

I{!=q

along

AB

is

z-t=a[</>+i(l{!-q)f

so that

x-t=a[</>2-(I{!_q)2],

y=2a</>(I{!-q). (2.50h)

The

condition (2.50e), i.e.

</>

=

y,

I{!

= 0

on

the

free surface gives im-

mediately

a =

-1/(2q)

from

the

second of (2.50h). Since

</>

= 0

on

BC

(2.50c)

the

first of (2.50h) gives

I{!

=

-[2q(x-t)]1/2+

q

on BC,

(2.50i)

where

the

I).egative sign is needed since

I{!

= 0

at

C on

the

free surface.

Also, combining (2.50e) with (2.50h)

on

FC

gives x - t = _(y2 _ q2)/(2q),

and so

xc=!q+t.

(2.50j)

Finally,

the

line integral (2.46) taken along the path FCB gives, by using

(2.50i), (2.50j) and

I{!

= 0,

.</>

= y on FC,

wB=w(t,O)=-f

I{!dx=~q2.

Xc

44

Free-boundary problems: formulation

Substitution of w =

~q2,

X = e in (2.50d) gives

yi

= iq2 +

2qe

which also

follows directly by rewriting (2.50g) and so the

flow

rate

q

is

confirmed by

the present derivation.

2.3.2. Rectangular dam with a sheetpile

The

dam shown in Fig. 2.3 has an impervious sheetpile along the

part

GE'

of the inlet face. This problem introduces a significant new feature.

The

point F where the free boundary meets the inlet face is not known a

priori. This means that the

flow

rate

q through

the

dam

is

not known, as in

the

two previous examples, but

is

an

additional unknown to

be

deter-

mined as

part

of the solution.

The

formulation

is

as follows where 0

is

again the

flow

region

ABCDFGA

and D

is

the

extended domain

ABEE'A:

</>x

= 0,

on

GF

apart from the points

G,

F,

<1>,;=0,

w=h~+q(XI-X)

on AB,

</>=Yl>

W=h~+qxl+!(Yl-y)2_hi

on

AG,

</>

=

Y2,

W

=!(Y2-

y)2

on

BC,

</>

=

y,

w = 0

on

CD,

</>

=

y,

a</>/an

= 0

on

FD,

w=O

on

D-n

including FD.

(2.51a)

(2.51b)

(2.51c)

(2.51d)

(2.51e)

(2.51f)

(2.51g)

(2.51h)

Since

AB

is

a streamline,

the

condition

Wx

(x, 0) =

-q

=

the

constant

discharge

rate

still holds

but

q is not known.

The

condition (2.51c)

follows as in §2.3.1 remembering that at B,

X=Xl>

y=O,

w=h~

from

Y

T

:'--------------

E

YI

G

t

D

C

Y2

·I

B

X

XI

FIG. 2.3.

Dam

with sheetpile

Other two-dimensional dams

45

(2.51e).

On

AG

we have

Wy

=-(</>-y)

and hence

[w

]~=

- r

(</>-1])

d1]

=lliYI-y)2].

But

w(O,O)=h~+qxlfrom

(2.51c) and so (2.51d) follows.

The

variational inequality (2.36)

is

to

be

satisfied by w(x, y) in the

present problem also. However, Baiocchi et al. (1973b) obtained the

mathematical result that, provided

q is chosen such that

q

~{Yi-Y~-(Yl-

AG)~/2xb

(2.52)

there

is a unique solution

Wq

and

there

is

a unique value of q in the range

defined in (2.52) for which

Wq

and its first derivatives are continuous on

the

boundary of

the

domain D. Baiocchi et

al.

(1973a) gave a discretized

interpretation of these mathematical statements which

is

convenient for

use in a numerical algorithm.

A suitable discretized form of the definition

of

q,

where

rf(X)

-q

=.10

<I>x(x,

1])

d1],

(2.53)

is

~

c/>ij -

c/>i-l,i

A

-q

= t..

~Y,

j=l

llx

i=l,

2,

...

,Nb

(2.54)

where N1llx =

Xb

N

2

lly

=

Yl'

The

corresponding

(2.22) is

</>i,j

= j

lly

+ (Wi,j-l-wi,j)/lly,

i=O,

1,

...

,N

b

discretized form of

j = 1, 2,

...

, N

2

•

(2.55)

Substitution of (2.55) into (2.54) with i = 1 and summing over

j leads

to

-q

llx

=

WI,O

-

WI,G

-

wo,o

+

WO,G

(2.56)

because

all intermediate terms cancel leaving only the W values for x = 0,

llx

at

y = ° and

at

y =

AG

denoted by

WO,G,

WI,G'

The

summation

terminates

at

the

lower edge of

the

sheetpile because

</>x

= ° on

GF

(see

2.51b). Using (2.51c) gives

(WI,O-WO,o)

=-q

llx

and so finally (2.56)

yields

WO,G

-

WI,G

= 0, which is a compatibility condition

to

ensure that

both

the

Dirichlet condition along

AG

and

the Neumann condition along

GF

are satisfied.

The

mathematical statement quoted by Baiocchi et al.

(1973a) can now

be

interpreted as implying that q must

be

chosen so that

a numerical solution satisfies

the

condition

(2.57)

where

fh(q)

is

a discrete analogy

to

the

continuous function of q in

the

46

Free-boundary problems: formulation

theoretical analysis.

For

a fixed q within the range specified in (2.52) the

Cryer algorithm will converge

to

the solution of the variational inequality,

for example, but (2.57) will not necessarily

be

satisfied. Baiocchi et al.

(1973a) inserted an outer iteration

on

q into the Cryer algorithms and

used the modified procedure detailed in §8.5.1(iii). They obtained several

sets of numerical results (see Tables 8.13-16).

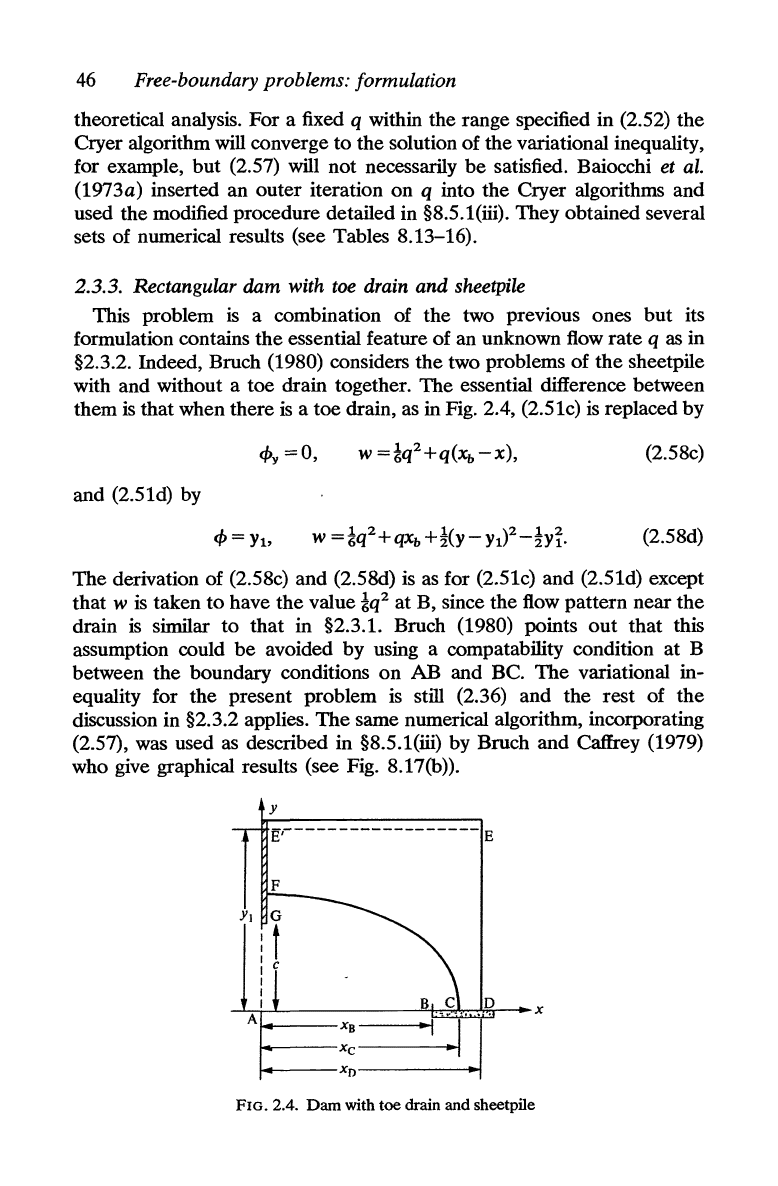
2.3.3. Rectangular dam with

toe

drain and sheetpile

This problem

is

a combination of the two previous ones

but

its

formulation contains

the

essential feature of an unknown flow

rate

q as in

§2.3.2. Indeed, Bruch (1980) considers the two problems of the sheetpile

with and without a toe drain together.

The

essential difference between

them is that when there

is

a toe drain, as in Fig. 2.4, (2.51c)

is

replaced by

<P

y

=0,

(2.58c)

and (2.51d) by

(2.58d)

The

derivation of (2.58c) and (2.58d)

is

as for (2.51c) and (2.51d) except

that

w

is

taken

to

have

the

value !q2 at B, since the flow pattern near

the

drain

is

similar

to

that

in §2.3.1. Bruch (1980) points

out

that

this

assumption could

be

avoided by using a compatability condition

at

B

between

the

boundary conditions

on

AB

and BC.

The

variational

in-

equality for the present problem

is

still (2.36) and the rest of

the

discussion in §2.3.2 applies.

The

same numerical algorithm, incorporating

(2.57), was used as described in §8.5.1(iii) by Bruch and Caffrey (1979)

who give graphical results (see Fig. 8.17(b)).

Y

E

r

-----------------

E

F

YI

G

: t

: c

I

-

~I~====~====~B~C~1D~~x

A:=====;;

..

,'-

~f

..

·I·

~----XD--------~

FIG. 2.4.

Dam

with toe drain and sheetpile

Other two-dimensional dams

47

2.3.4.

Dam

with inlet face slanted

The

different geometry of this dam, depicted in Fig. 2.5, gives rise to

new features in

the

formulation. Although

<b(x,

y) still has the constant

value

Yl

along

AF,

the Dirichlet condition (2.29) for w on

AF

can no

longer

be

obtained by the integration leading to

w(O,

y). Instead we have

a Neumann condition

Wy

=

Y-Yl

on

AF,

(2.59a)

in which

w(x, y)

is

redefined

to

be

(2.59b)

Here

the

flow

rate

q

is

again unknown and

is

contained in the boundary

condition

on

AB

which

is

~(x,O)=O,

w(x,

O)=-q(x-xl)+h~,

(2.59c)

Also

(2.59d)

Other

definitions in

the

extended domain D, taken to

be

the trapezium

AFEB, and conditions

on

its boundary except

AF

are as for the simple

dam §2.2.3, but

the

variational inequality

is

more complicated.

For

test

functions

vex,

y) which agree with w(x, y) on

the

boundary of D except

AF

and otherwise have the properties of §2.2.4, the variational inequality

is

Y

--~--~~-~---------------------E

IF

I

Y2

__

~_~L_

_____________

~~L_~x

I..----------xl------------+I

FIG. 2.5.

Dam

with front face slanted

(2.60)

48

Free-boundary problems: formulation

where now, with

the

suffix q temporarily dropped for convenience,

a(w,

v-w)"'"

J

J{wx[v-w1

+wJv-wl,

D

and

fJ

y2+X2JF

(v-w)=-

[v-w]dxdy+-l

__

f

(Y-Yl)(v-w)dy.

-

XfYl

A

D

(2.60b)

A proof is outlined below

but

first we remark

that

Baiocchi et ai.

(1973a)

quoted mathematical results for this problem similar

to

those in

§2.3.2 including restrictions

on

q.

There

is a unique value of q for

q;;::.

-

y~/(2Xl)

for which (2.60) has a unique solution

Wq

which, together

with its first derivatives, is continuous on

the

whole boundary of D.

The

compatability condition

at

F corresponding

to

(2.5-7)

and obtained in

the

same way

is

(2.61)

which is

to

be

incorporated in

the

numerical algorithm discussed in

§8.S.1. Baiocchi

et ai. (1973b) and Bruch (1980) base a proof of

the

ineqUality (2.60) on

the

form of Green's theorem

J

J{I~V2w

- V .

[g{3Wy

-

g{3w

x

] +

V{3

. Vw}dx dy

D

=1

{{3[W

x

-gw

y

]dy-{3[w

y

+gw

x

]dx}, (2.62)

ilD

where g =

Yl/XF,

the

slope of

the

inclined face and where again

the

suffix

q has been dropped for convenience, i.e. w

"'"

w

q

•

For

the

boundary lines

AB,

BC, CE, and EF,

{3

= v - w = 0 and so, remembering (2.S9a),

the

right-hand side of (2.62) reduces.to an integral

IAF

along

AF

only, given

by .

(2.63)

since

dx

"'"

(XF/Yl)

dy along AF.

The

second integral over

the

domain D

Other two-dimensional dams

49

on

the

left-hand side of (2.62) can

be

expanded as follows:

-I I V .

(g(3Wy

-

g(3w,,)

dx dy = - I I

{(3[g.,w

y

-

gy

w,,]

D

+

g[f3x

Wy

-

(3y

w,,]

+

g(3[

W"y

- W

y

,,])

dx

dy

= - I

I{g[f3x

W

y -

(3yw,,])

dx dy (2.64)

D

since g =

Yl/XF

and the first derivatives

of

W are continuous. Finally we

recall

that

I J

(3V

2

w dx dy

:,.;;;

I J (v -

w)

dx dy,

(2.65)

D

and combine (2.63), (2.64), and (2.65)

to

establish (2.60).

We

note that

(2.60)

is

associated with a non-symmetric bilinear fonn and so this

problem cannot

be

fonnulated as a minimization problem. Accordingly,

Baiocchi

et

al.

(1973a) approximated the complementarity fonnulation as

in §8.5.1(iii) and this

is

convenient for use of (2.61). The matrix in the

successive overrelaxation method (SOR) with projection

is

no longer

symmetric but the method

is

still convergent. Miellou (1971) and Baioc-

chi

et

al.

(1973a) present some numerical results and a demonstration of

convergence for

one

particular dam (see Table 8.17).

2.3.5.

Dam

with inlet face slanted and a

toe

drain

Sloss and Bruch (1978) obtained numerical results for this problem but

Bruch (1980) quoted an alternative

fonn

of variational inequality in

which, with reference to (2.60),

a(w,

v-w)=

J I{Vw .

V(v-w)-

g[(v-w)xWy

-(v-w)yW

x

]

D

+(v-

w)[-g.,w

y

+ gyw,,]}dx dy, (2.66a)

II

J

F (y2+

X2)

(v-w)=-

(v-w)dxdy+

1\.

(V-W)(Y-Yl)

~FY1F

dy,

D

(2.66b)

where now g

= y/x. A uniqueness proof was given by Bruch (1980). Sloss

and Bruch (1978) showed results agreeing well with Polubarinova-

Kochina's (1962) analytical solution for

one

dam and with results of

Jeppson

(1968c) and

of

Shaug and Bruch (1976), who used an inverse

fonnulation, for a second dam (see Table 8.18 for iteration details).

50 Free-boundary problems: formulation

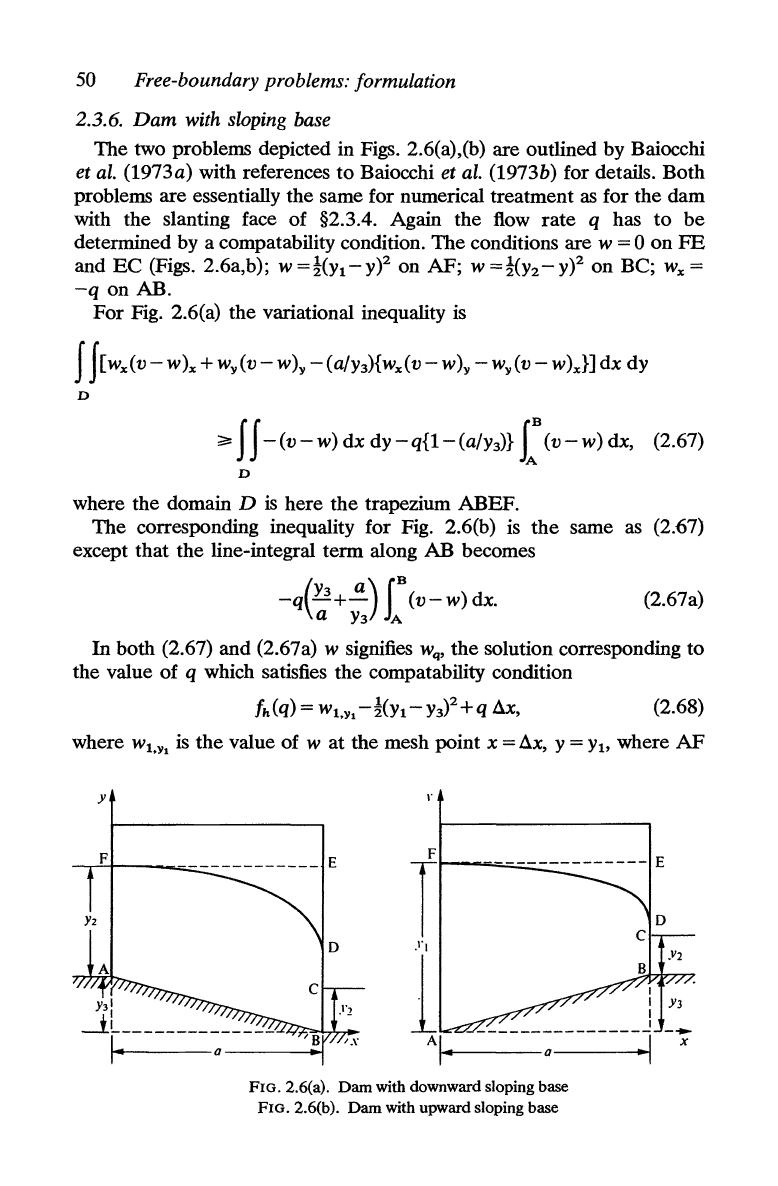
2.3.6.

Dam

with sloping base

The two problems depicted in Figs. 2.6(a),(b) are outlined by Baiocchi

et al. (1973a) with references

to

Baiocchi et al. (1973b) for details. Both

problems are essentially the same for numerical treatment

as

for the

dam

with the slanting face of §2.3.4. Again the flow

rate

q has

to

be

determined by a compatability condition. The conditions are w = 0

on

FE

and

EC

(Figs. 2.6a,b);

w=t(YI-yf

on AF;

w=t(Y2-yf

on

BC; W

x

=

-q

on

AB.

For

Fig. 2.6(a) the variational ineqUality

is

J J [wAv - w)x + wy(v -

w)y

- (a/Y3){wAv -

w)y

-

Wy(v

- w)x}]

dx

dy

D

~

JJ-(V-W)dXdy-q{1-(a/

Y3

)}

f(V-W)dX,

(2.67)

D

where the domain D

is

here

the

trapezium ABEF.

The

corresponding inequality for Fig. 2.6(b)

is

the

same as (2.67)

except that the line-integral

term

along AB becomes

_q(Y3+~)

J\V-W)dX.

(2.67a)

a

Y3

A

In

both (2.67) and (2.67a) w signifies w

q

,

the

solution corresponding to

the value of

q which satisfies the compatability condition

fh(q) =

Wl,y,

-t(Yl-

Y3f+q

.:lx,

(2.68)

where

Wl,y,

is the value of W at the mesh point x =

.:lx,

Y =

Yt>

where

AF

y r

--------------

E

c

Y3'

-1L

______________

'-"4'.z>.IhJ,-,..

I..

a-------t

~-------a------~

FIG. 2.6(a).

Dam

with downward sloping base

FIG. 2.6(b).

Dam

with upward sloping base

o

Y2

YJ

--

x

Other two-dimensional dams

51

'--1--~--~-=---------------

E

~~~Ex

~1·----·xl-----+J

FIG.2.6(c). Dam with sloping base and inlet face

and

BE

are lines on a mesh with increments

Ax,

.Ay

where

.Ay/Ax

=

Y3/a.

Baiocchi

et

al.

(1973a) give results for one example of each dam (see

Tables 8.19, 8.20).

The

problem of the

dam

with a sloping base and a sloping inlet face

(Fig.

2.6(c»

contains a jump discontinuity in a fixed-boundary condition

which precludes a variational formulation. Thus Baiocchi's transformation

for the problem depicted in Fig. 2.6(c) leads to

the

equations

~w=Xo

in D

W=O

in

D-n,

Wx

=-q

on AB

Wy=Y-Yl

onAF,

W>O

in

n,

W

=!(Y2-y)2

on

Be,

W=O

on

CE

and FE.

(2.69a)

(2.69b)

(2. 69c)

(2.69d)

(2.6ge)

The jump discontinuity occurs in the direction of the oblique derivative as

shown by (2.69c) and (2.69d) on

AB,

AF

excluding the

end

points.

In

a

manner analogous to

the

use of an enthalpy function in Stefan problems,

e.g. equations (6.6), (2.69a), and (2.69b) can

be

combined into the

non-linear equation

~wEH(w)

inD,

(2.69f)

where

H(w)~O,

w<0,0:S;;H(w):S;;1,

w=O,H(w)=

1,

w>O.

A discretized form of (2.69f) can

be

written as

{f}-[A]{W}EH({w})

where

{f}

is

the vector containing the known terms from the boundary

conditions and

[A]

is

an irreducibly diagonally dominant matrix with

components

O-;j

:s;;0,

if

j and

O-;i

>0.

Thus

n

/;

- L

O-;jWj

EH(wt),

j=l

i = 1, 2,

...

,

n,

where n

is

the

number of points in the discretization of D.

Crank J. Free and Moving Boundary Problems

Подождите немного. Документ загружается.