Crank J. Free and Moving Boundary Problems

292

Analytical solution

of

seepage problems

y

(a)

(b)

B

FIG. 7.7. Triangular dam with no tail water

flow region

ABC

in

the

z-plane

is similar

to

A''B''C' in

the

w plane

and

so w = C1z, where C

1

is a constant.

For

point B, z = H + iH, w =

!(1

+

i)

=

llx -

iqy;

hence C

1

=

1/(2H)

and

w = z/(2H) =

-dgdz.

Integration gives

{=-z2/(4H)+C

2

and

since for point B,

cf>=H,

I{i=O,

we find

{=

-z2/(4H)+!H(2+i).

Finally,

cf>

=

(4IP-x

2

_y2)/(4H),

I{i

=

(IP-xy)/(2H),

so that

the

equipotentials

are

given

by

x

2

-

y2

= constant

and

the

stream-

lines

by

xy = constant.

We

can identify

the

following successive steps in

the

hodograph method

of

solving flow problems.

(a)

Map

the

boundary

of

the

flow domain

in

the

z-plane

on

to

the

hodograph w-plane by applying

the

rules (i-iv)

or

more

general

ones

if

need

be.

(b) Reflect this contour in

the

w-plane in

the

real axis llx

to

obtain

the

mapping from

the

z-plane

to

the

w-plane. This is a conformal

mapping.

(c)

Map

the

boundary

of

the

flow domain in

the

z-plane

on

to

the

complex potential {-plane.

(d)

Find

a conformal mapping relationship w =

w({)

that

maps

the

w-plane

on

to

the

{-plane.

(e)

Use

(7.14) in

the

integrated form

1

,

d{'

.

z =

'0

w({')

= x +

'y,

x=y=O.

(7.15)

Although theoretically

there

is a transformation which will

map

any

pair

of

simply connected regions

on

to

each

other

it

may

not

always

be

possible to find

the

expression which maps

the

complicated flow region

directly

on

to

the

complex potential plane as required in step

(c)

above.

However, by introducing

one

or

more

auxiliary planes

and

mapping

functions, even complicated flow regions

have

been transformed into

regular geometric shapes. Usually these are polygons having a finite

Hodograph method: conformal transformations

293

number of vertices,

one

or

more of whieh may

be

at infinity.

The

interior

of a polygon can

be

mapped

on

to

the

upper half of another plane by the

Schwarz-Christoffel transformation. Thus the flow domains in the

w and

, planes are both mapped on

to

an auxiliary g plane by functions

w = w(g) and

,=

,(g)

respectively.

The

Schwarz-Christoffel and other

transformations

are

now described.

7.3.2.

Some useful transformations

(i)

Schwarz-Christoffel transformation. This transformation is central to

the analytical solution of problems in porous

flow:

it transforms the

interior of a polygon in

the

z-plane into the upper half of another

{;-plane,

g =

IJ.

+

iv,

in such a way that the sides of

the

polygon are

transformed into

the

real axis of the {;-plane.

We start from

the

expression

dz

d{;

=

A({;

-

at)c/>l({;

-

~c/>2

...

({;

-

a,,)c/>n,

(7.16)

where A

is

a complex constant and

at>

lIz,

...

,

a",

q,t>

ch.,

...

,cf>..

are real

numbers such that

a"

> a,,-t >

...

> a

2

>

at.

The real numbers

at>

a

2

,

•••

,

a"

are plotted

on

the real axis of the {;-plane in Fig. 7.8a.

If

{;t

is

a real number then

We know that

{

0,

{;>a,

arg({;

- a,) =

'7T,

{; < a,.

arg(dz/d{;) = arg A + q,t

arg({;t

- at) +

...

+

q,n

({;

-

a,,)

(7.17)

(7.18)

and so on writing 6

r

= arg (dzld{;) when

a,

< g < a,+t and using (7.17) and

(7.18) we have

(a)

("

-plane

Y (b)

z -plane

'1

x

FIG. 7.8. Schwarz-cbristoffel transfonnation

294

Analytical solution

of

seepage problems

But

dz

dx+i

dy

-1

dy

arg

d~

= arg

d""

tan

dx

'

which

is

the angle that the element

dz

in the z -plane, into which

d~

is

transformed by (7.16), makes with

the

real axis of

the

z-plane. Thus

as

the

point

~

traverses the real axis of

the

~-plane,

the corresponding point

z descnbes a polygon in

the

z-plane as shown in Fig. 7.8b. When the

point

~

passes from left

to

right of

a..+1

in the

~-plane,

the

direction of

movement of

the

point z in

the

z-plane changes by an angle of -'lTc/>r+1 in

the

sense indicated in Fig. 7.8b.

If

the interior angle of

the

polygon

is

G:

r

+ 1 we have 0:.+1 -

'lTc/>r+

1 =

'IT

and (7.16) becomes after integration

z

=AJ

(~-al)'·,/""-l(~_~ai""-l

...

(~_tIn)aft/""-l

d~+B,

(7.19)

with

B an arbitrary constant.

The

Schwarz-Christoffel expression (7.19)

transforms

the

real axis of

the

~-plane

into a polygon in the z-plane, with

interior angles

0:.: the modulus and argument of A determine

the

size and

orientation respectively of

the

polygon and its location is determined by

the

constant B.

We

have been considering only a simply connected polygon, but its

boundaries may extend to infinity.

It

is

known that, in mapping a polygon

of

n sides, three of

the

values

at>

a2'

...

,

tIn

can

be

assigned arbitrarily,

leaving

n - 3 to

be

determined.

In

the

commonly occurring case of a

polygon with a vertex at infinity, mapping

to

~=oo, dz/d~

contains one

less term and one less parameter than usual, and only two of the

n-1

points

at>

a2,

...

, tIn-l can

be

specified arbitrarily.

(ii) Inverse transformation. This is frequently of use in

the

hodograph

method. With reference to Fig. 7.9,

the

point P is mapped on to

P'

such

y

/,'--

--..

.......

,

/ ,

/ \

I \

I

(O,~)

\

A

x

FIG. 7.9. Inverse transformation

Hodograph method: conformal transformations

295

that

OP

.

OP'

= p2

and

P'

is

the

image

of

P in

the

circle C with centre 0

and

radius

p.

Thus

z'

= x' + iy' = p2/(X - iy), i.e. with z = x - iy,

(7.20)

Application

of

(7.20) maps points

on

the

circle C

on

to

themselves,

the

centre

of

C maps

to

a point

at

infinity,

and

any circle

not

centred

at

0 and

any straight line

map

on

to

a circle

or

a straight line. A circle C (Fig. 7.9)

passing through

the

origin 0 transforms into

the

straight line passing

through

the

points

of

intersection

AB

of

the

two circles.

(iii) Zhukovski's function. This function shares with

the

hodograph trans-

formation

the

property

that

the

geometry

of

the

flow region is known in

the

new plane. Zhukovski (Polubarinova-Kochina 1962;

Harr

1962;

Bear

1972) defined a function 6

1

given for an isotropic homogeneous medium

by

6

1

= cf>-y

and

which apart from a multiplying constant is

the

pressure (see equation

(2.5) in §2.2).

The

function 6

1

is harmonic in

the

vertical

x,

y plane

and

a

conjugate function 6

2

=

I{i

+ x can

be

defined, so

that

there

is a complex

function 6

6 = 6

1

+ i6

2

= , + iz,

z

=x+iy.

(7.21)

Since

cf>

= y along

both

the

free surface

and

the

seepage face

and

hence

6

1

=0,

these two surfaces

map

on

to

the

ordinate axis (6z)

in

the

6-plane,

with axes 6

1

and

6

2

parallel

to

x

and

y axes respectively.

The

function 6 is

Zhukovski's function

or

.the complex pressure.

We

have, by differentiat-

ing (7.21),

dz

1

-=---

d6

w-i'

z=J

~6+

.,

-w

l

(7.22)

so

that

once

the

mapping

of

6

on

to

w is known, (7.22) yields a

relationship between 6

and

z from which

cf>(x,

y)

and

I{i(x, y) follow

immediately. Aravin

and

Numerov (1965) used a Zhukovski function 6

defined as 6 = z - i', so

that

the

free

and

seepage surfaces map

on

to

the

real axis of

the

6-plane.

(iv) Hamel's function.

Hamel

(1934) introduced a mapping function T

defined by

T=

T+i6 =

-In(-d

2

,/dz

2

).

(7.23)

We

have

the

basic relationships

_ d

2

,

=

_~

(d

n

= _ d(dGldz)/dt

4x

-

iiI

y

dz

2

dz

d~)

dz/dt n(llx + iqy)'

296 Analytical solution

of

seepage problems

where

qx,

qy

are time derivatives of

q",

qy

and n

is

the

porosity connecting

qx,

qy

with

X,

Y respectively. By defining

4c

-

iqy

=

nAe-

i13

,

qx

+

iqy

=

qe"'-,

where

q2=q~+q;,

(nA)2=q~+q;,

and

a,

~

are moduli we express

T+i6

as

T+i6=-ln(A/q)+i(a+m

and hence

T =

-In(A/q),

6 _

{a

+~,

A/q

>0

a+~-7f',A/q<O.

The

various boundaries of

the

flow region in

the

z -plane can now

be

mapped on to

the

T-plane. We consider as an example a streamline

or

an

impervious boundary making

an

angle a with

the

x-axis. Along such a

boundary dy/dx

=

qiq"

= tan a and hence

d

2

, d(q" -

iqy)

dq"

. .

--d

2=

d(

.)

-d

(cos2a-zsm2a),

z

x+zy

x

so that

T + i6 =

-In{(dqJdx)e-

2iot

}.

For

dqJdx

>0,

6 =

2a

+

2m7f';

dqJdx

<0,

6 =

2a

+ (m -1)7f'. In each case

T = -In{(dqJdx)cos

2a}.

For

an equipotential boundary similar argwnents yield

6

=

{-tan-

1

(cos

2a/tan

2a)+2m7f', dq,,/dy

>0,

-tan-

1

(cos

2a/tan

2a)+(2m-l)7f',

dqJdy

<0,

For

a seepage face making an angle a with the x-axis the condition

-q"

cos a -

qy

sin a = sin a leads

to

the same expressions for 6 as for an

equipotential boundary.

For

a steady free surface, the condition

q~+q;+qy=O,

i.e.

dqJdqy=-(2qy+l)/2q",

remembering that dqJdqy = dy/dx, gives

d

2

,

dqy

[-{(2qy +

1)/2q,,}-

i]

-

dz

2

= dx

l+i(qiq,,)

dqy

[(2q"qy

+~q,,)+

i(q~-q;-~qy)]

=-

dx

qy

dqy

e-

3iot

=

dx

2sina'

since along

the

free surface

q"

=

-sin

a cos

a,

qy

=

-sin

2

a.

For

dqidx>

0,

6=3a+2m7f';

dqidx<O,

6=3a+(2m-l)7f'.

The

successive steps in

Hodograph method: conformal transformations

297

the

solution of a flow problem are first to map the z-plane

on

to the

hodograph w-plane, and record the values of

()

on

the

various parts of the

hodograph boundary by using

the

expressions just obtained. Next

The

w-plane

is

mapped

on

to

the

~-plane

(~=

p.,

+ iv), using a modular elliptic

function and an intermediate transformation in such a way that

all the

boundaries of

the

flow region are mapped

on

to the real axis of the

~-plane.

Values of T = 'T + i6 are deduced

at

all points of

the

~-plane

from

the

values of 6 along

the

real

axis

by using the Poisson integral

. . . 1 1

00

6(p.,)(~p.,

+ 1)

IT=

6-l'T=-l'To+

wi

-00

(p.,-~)(1+p.,2)

dp.,

where 'To

is

an arbitrary constant. Thus we obtain

T=Fl(~)'

From the

function which maps w on the

~-plane

we deduce

T=Fiw);

but

T=

-In(dw/dz) and so we can write

z =

f

eXP{~;iw)}

+C

1

=F

3

(w),

c=-

f

F3

1

(z)

dz+~,

from which follow q."

qy,

cf>(x,

y),

I/I(x,

y) and

the

equation for the free

surface. Muskat (1935) computed solutions for six simple dam problems

using Hamel's transformation.

The

z-plane, w-plane, and

~-plane

are

shown in Figs. 7.10a,b,c. His solution for z as a function of w

is

f[

1-~

]!

{ 3

[l~(p.,)dp.,}

-

z=C

~(~-a)(~-b)

exp

-2w.o

p.,_~

dw,

(7.24)

where

p.,

is

the real axis of

the

~-plane

and

~(p.,)

a function evaluated in

the

process of solution.

(a)

z-plane

;tkJ

Ll1

A

B4

x

(b) w-plane

-qy

D~~--~----~--~C

--c

(c)

,-plane

v

FIG. 7.10. Hamel's transformation forsimpie dam problem

7.3.3. Trapezoidal drainage ditch

An

example

to

illustrate

the

use of the transformations (i), (ii), (iii) above

is afforded by seepage from a trapezoidal ditch in which the water level

is

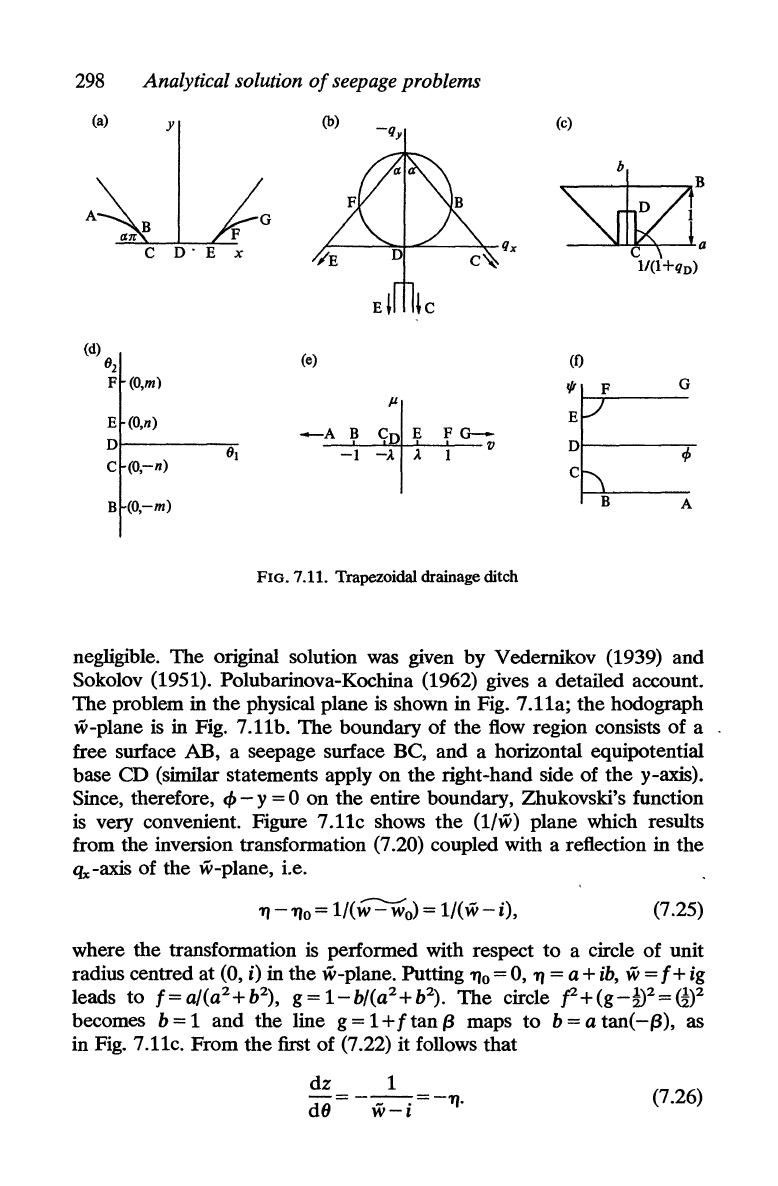
298

Analytical solution

of

seepage problems

(a)

y

A

(d)

e

l

F

(O,m)

E

(O,n)

DI------eT!

C (O,-n)

B (O,-m)

(e)

P

-A

B CD E F

G-

-1

-A

A v

FIG.

7.11. Trapezoidal drainage ditch

(c)

(0

:E

G

D

'"

C

B A

negligible. The original solution was given by Vedernikov (1939) and

Sokolov (1951). Polubarinova-Kochina (1962) gives a detailed account.

The problem in

the

physical plane

is

shown in Fig.

7.lla;

the

hodograph

w-plane

is

in Fig. 7.11b. The boundary of the flow region consists of a

free surface AB, a seepage surface BC, and a horizontal equipotential

base

CD

(similar statements apply

on

the

right-hand side of the y-axis).

Since, therefore,

cf>

- y = 0 on the entire boundary, Zhukovski's function

is

very convenient. Figure

7.llc

shows

the

(1/w)

plane which results

from the inversion transformation (7.20) coupled with a reflection in the

lJx

-axis of the w-plane, i.e.

(7.25)

where the transformation

is

performed with respect

to

a circle of unit

radius centred at (0,

i)

in

the

w-plane. Putting

110

= 0,

11

= a +

ib,

w = f + ig

leads to

f=

a/(a

2

+b

2

),

g =

1-b/(a

2

+b

2

).

The

circle

.f+(g_~?=G)2

becomes

b=l

and the line

g=l+ftan/3

maps

to

b=atan(-/3),

as

in Fig. 7.11c. From

the

first of (7.22) it follows that

dz

1

dB = -

w-i

=-11·

(7.26)

Hodograph method: conformal transformations

299

The

appropriate Schwarz-Christoffel transformation (7.19)

is

1

~

f dg'

'f/=M

(1_~'2)a+~(,,?_~'~1

a+

N

,

where A

is

defined

in

Fig.

7.l1e.

Polubarinova-Kochina (1962) gave the detailed evaluation of the con-

stants M and

N.

Briefly, the values of

'f/

are found using (7.25) at

the

points

~

= ° and

~

= 1, which correspond to points D and B in the

hodograph plane.

At

~

= 0, W =

-iqo,

where

qo

=

qy

at

D,

and so N =

i/(qo + 1). For

~

=

A,

W =

00,

i.e.

'f/

= 0, and

we

have

1

~

fdf

'f/

=M

~

(l-f~a+~A2_,'2)1-a·

To

find real values of the integrand for A <

~

< 1, we note that in passing

from

CD

to

CB by contouring C in the lower half-plane anti-clockwise

through angle

1T

we have

(~_

A)l-a

e

'lri(l-a)

=

_(~

_ A)l-a

e

-'Irio:

and so

'f/

becomes

olE

~'~'

'f/

=-M

e

'Jf1Cl.

~

(1-f~a~(e-A2)1-a·

For

~

= 1 and point B in

the

hodograph plane we find

which leads to

ie'lrio:

'f/1=--

cos 1Ta

i

11

-~d~

COS1Ta

=-M

~

(l-e)a+~(~2-A2)1

a

-MJ,

where after the substitution

1_~2=A'2X,

with A

2

=1-A,2

_~

11

-a-~

_ a-1

_~

1T~r(a)

1-

2A

, x

(1

x)

dx-

2

A'cos1Tar(a+t)'

(7.27)

following some manipulation of

(3

and

r functions. Thus M

is

determined

from (7.27) and

dz

. 2

IE

fdf

i

d6=-'f/=-2A

•

.J(1-A)

(l_C'2)a+!(A

2

-f

2

)1-a+

qo+1'

(7.28)

where A =

r(a

+t)/1T!r(a).

300

Analytical solution

of

seepage problems

Next the 8-plane shown in Fig. 7.11d must

be

mapped

on

to

the

g-plane.

The

complex potential

'-plane

is

shown in Fig. 7.11f. The flow

region corresponds to

the

half-plane in the 8-plane and using the facts

thatfor

g = 0,

cf>

= 0,

1/1

= !Q, x = 0, and for g = 1,

cf>

+ y = 0,

1/1

= 0, x =

XF,

the linear transformation leads

to

(7.29)

where

Q

is

the total flow through

CE

in Fig. 7.11a. Integration of (7.28)

using (7.29) and (7.22) gives

- - -

2\~

i~

i~2

gl dg

1

XF+

Q

z -

A(l

A.)

(XF+

Q)

dg

2

(1-

gi)a+~(A.

2_

gi)l-a

+ 2(qD+

1)

g.

(7.30)

From this we can relate

z

to

the

complex potential , via the Zhukovski

function

8.

Vedernikov (1939) examined the ditch with vertical sides in

more detail and Sokolov (1951) extended

the

analysis of (7.30) by making

further transformations.

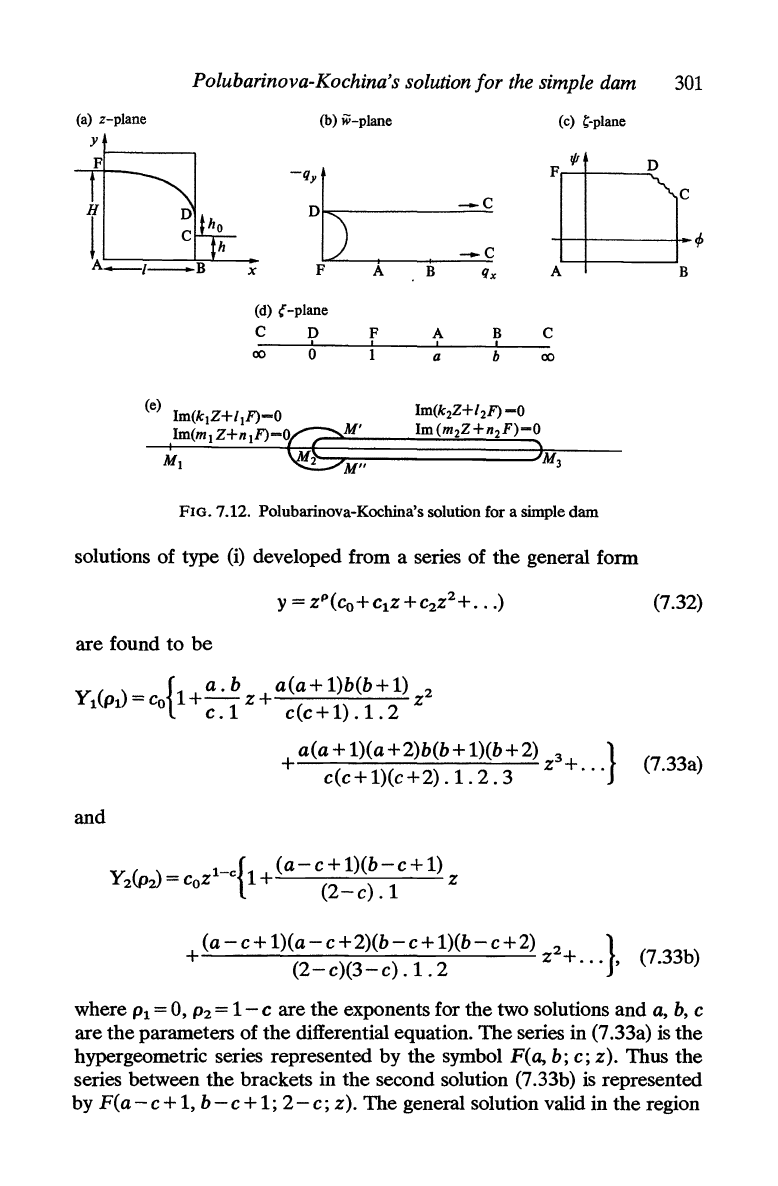
7.4.

Polobarinova-KodUna's solution for the simple

dam

Polubarinova-Kochina (1938,1939) and Risenkampf (1940) applied

the theory of linear differential equations to some problems of ground-

water

flow.

A general treatment

is

given by Polubarinova-Kochina (1962)

and applied

to

the

problem of

the

simple dam and other more difficult

problems. The hodograph

and

complex potential planes are still involved

but solutions of the hypergeometric equation are introduced. Here we

confine attention to

the

simple dam problem depicted again for conveni-

ence in Fig. 7.12a, together with

the

hodograph w-plane, the complex

potential ,-plane, and an auxiliary g-plane in Figs. 7.12b,c,d

respectively.

We

first review some relevant properties of

the

hypergeometric equation

d

2

y

dY

z(l-z)

dz

2

+{c-(a+b+l)z}

dz

-abY=O,

(7.31)

and its solutions in the form of hypergeometric series. Equation (7.31)

has three regular singularities

at

the points z = 0, 1, and

00.

There are

three kinds of solutions in

the

forms of power series: (i) a solution in a

series of powers of

z,

centre z = 0, and valid within a circle of unit radius;

(ii) a solution in a series of powers of

1-

z,

centre z = 1, and valid within

a circle of unit radius;

(iii) a solution in a series of powers of 1{z, centre

z

=0,

and valid outside a circle of unit radius.

The

two fundamental

Polubarinova-Kochina's solution for

the

simple dam

301

(a)

z-plane

y

pt------,

(b) w-plane

D~

________

~--~C

x

(d)

(-plane

C D

00

b

A

p

1

_C

B

A

B

I I

a b

Im(k

2

Z+1

2

F)-O

Im(m2Z+n2F)-O

(c)

~-plane

'"

P

A

C

00

)M

3

FIG. 7.12. Polubarinova-Kochina's solution for a simple dam

solutions of type

(i)

developed from a series of

the

general form

are found to be

Y(

)

-

{1+a.b

a(a+1)b(b+1)

2

1P1-

C

O

1Z+

(

1)

12

Z

c.

c c+

..

a~+D~+~b~+D~+~

3 }

+

c(c+1)(c+2).1.2.3

Z +

...

and

Y

(p

\-

1-C{1

(a-c+1)(b-c+1)

221-

C

OZ +

(2-c).1

Z

D

C

B

(7.32)

(7.33a)

(a-c+1)(a-c+2)(b-c+1)(b-c+2)

2 } (7.33b)

+

(2-c)(3-c).1.

2 z +

...

,

where

P1

= 0,

P2

=

1-

c are

the

exponents for the two solutions and

a,

b,

c

are

the

parameters of

the

differential equation.

The

series in (7.33a)

is

the

hypergeometric series represented by

the

symbol F(a, b; c; Z). Thus

the

series between

the

brackets in the second solution (7.33b) is represented

by

F(a

- c + 1, b - c + 1; 2 -

c;

z).

The

general solution valid in

the

region

Crank J. Free and Moving Boundary Problems

Подождите немного. Документ загружается.