Цыпкин А.Г., Пинский А.И. Справочное пособие по математике с методами решения задач для поступающих в вузы
Подождите немного. Документ загружается.

468 Г л а в а 14. Метод координат и элементы векторной алгебры
При таом определении равенства веторов множество всех
веторов, равных , называют свободным ветором. Поня-
тие свободноо ветора можно таже связать с отображени-
ем пространства на себя, при отором все точи пространства
перемещаются в одном и том же направлении (направлении )
на одно и то же расстояние (длину AB). Определенный уазан-
ным образом свободный ветор называют таже параллель-
ным переносом, оторый полностью задается упорядоченной
парой несовпадающих точе A и B.
Любая пара совпадающих точе определяет тождественное
отображение пространства или нлевой ветор.
Линейными операциями над веторами называют опера-
ции сложения и вычитания веторов, а таже умножение ве-
тора на число.
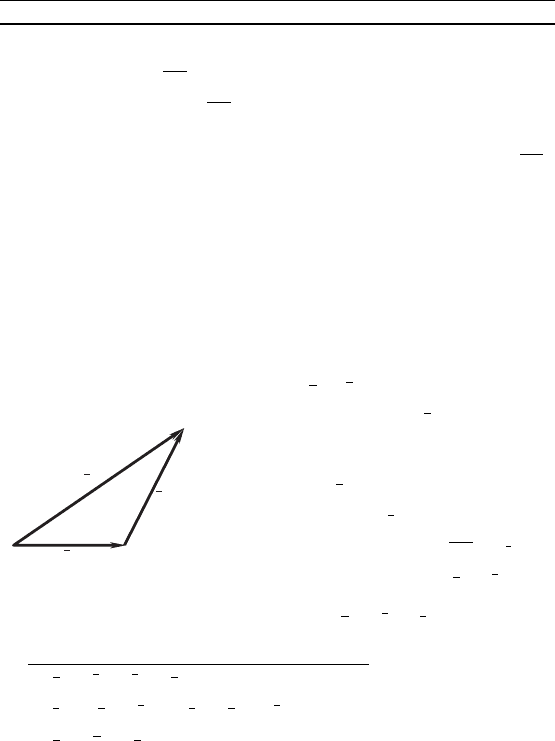
Пусть и — два ненулевых ве-
тора. Отложим ветор от неоторой
точи O и обозначим ео онец бу-
вой A (рис. 61). Затем отложим от точ-
и A ветор и обозначим ео онец
бувой B. Ветор с началом в точ-
е O и онцом в точе B ( = ) на-
зывают сммой веторов и :
+ = .
Свойства операции сложения веторов
:
1) + = + ;
2) + ( + ) = ( + ) + ;
3) + = .
Приведенное выше правило сложения веторов называют
правилом треольниа (сумма веторов представляет собой
третью сторону треуольниа, в то время а слааемые обра-
зуют две друие стороны треуольниа; рис. 61). Наряду с этим
правилом существует та называемое правило параллело-
рамма, при отором слааемые веторы отладывают от од-
ной точи, через их онцы проводят отрези прямых и в ре-
зультате получают параллелорамм (рис. 62), диаональ ото-
роо, проходящая через общее начало веторов, и равна сумме
веторов.
AB
AB
AB
c
A
B
b
Oa
Рис. 61
a
b
a
b
c
OB c
a b
a b c
a b b a
c a b c a b
a 0 a
§ 79. Простейшие задачи векторной алгебры 469
Ветором, противоположным ветору , называют ветор
(– ) таой, что сумма веторов и – равна нулевому ветору:
+ (– ) = .
Ненулевые противоположные веторы имеют равные длины и
противоположные направления.
Разность двух веторов – есть сумма ветора и ве-
тора, противоположноо ветору , т. е.
= + (– ).
Разность веторов можно получить с помощью правила тре-
уольниа. Отложив от точи A ветор (рис. 63), получим
= . Затем от онца ветора отложим ветор =
= – . Ветор = — разность веторов и :
= – .
Ветор разности двух веторов можно таже выразить а вто-
рую диаональ BA параллелорамма ABCD (см. рис. 62).
Произведением ненулевоо ветора на число λ − 0 на-
зывают ветор, имеющий направление ветора , если λ поло-
жительно, и противоположное направление, если λ отрица-
тельно; длина этоо ветора равна произведению длины вето-
ра на абсолютную величину (модуль) числа λ.
Свойства операции умножения ветора на число
:
1) (λ
1
λ
2
) = λ
1
(λ
2
);
2) λ( + ) = λ + λ , (λ
1
+ λ
2
) = λ
1
+ λ
2
;
3) 0 · = ;
4) λ = .
A
BC
b
O
a
OC a b,+=
BA a b,–=
Рис. 62
A
b
–bc
C
B
a
Рис. 63
a
a a a
a a 0
a b a
b
c a b
a
AB a AB BC
b AC c a b
c a b
a
a
a
a a
a b a b a a a
a 0
0 0

468 Г л а в а 14. Метод координат и элементы векторной алгебры
При таом определении равенства веторов множество всех
веторов, равных , называют свободным ветором. Поня-
тие свободноо ветора можно таже связать с отображени-
ем пространства на себя, при отором все точи пространства
перемещаются в одном и том же направлении (направлении )
на одно и то же расстояние (длину AB). Определенный уазан-
ным образом свободный ветор называют таже параллель-
ным переносом, оторый полностью задается упорядоченной
парой несовпадающих точе A и B.
Любая пара совпадающих точе определяет тождественное
отображение пространства или нлевой ветор.
Линейными операциями над веторами называют опера-
ции сложения и вычитания веторов, а таже умножение ве-
тора на число.
Пусть и — два ненулевых ве-
тора. Отложим ветор от неоторой
точи O и обозначим ео онец бу-
вой A (рис. 61). Затем отложим от точ-
и A ветор и обозначим ео онец
бувой B. Ветор с началом в точ-
е O и онцом в точе B ( = ) на-
зывают сммой веторов и :
+ = .
Свойства операции сложения веторов
:
1) + = + ;
2) + ( + ) = ( + ) + ;
3) + = .
Приведенное выше правило сложения веторов называют
правилом треольниа (сумма веторов представляет собой
третью сторону треуольниа, в то время а слааемые обра-
зуют две друие стороны треуольниа; рис. 61). Наряду с этим
правилом существует та называемое правило параллело-
рамма, при отором слааемые веторы отладывают от од-
ной точи, через их онцы проводят отрези прямых и в ре-
зультате получают параллелорамм (рис. 62), диаональ ото-
роо, проходящая через общее начало веторов, и равна сумме
веторов.
AB
AB
AB
c
A
B
b
Oa
Рис. 61
a
b
a
b
c
OB c
a b
a b c
a b b a
c a b c a b
a 0 a
§ 79. Простейшие задачи векторной алгебры 469
Ветором, противоположным ветору , называют ветор
(– ) таой, что сумма веторов и – равна нулевому ветору:
+ (– ) = .
Ненулевые противоположные веторы имеют равные длины и
противоположные направления.
Разность двух веторов – есть сумма ветора и ве-
тора, противоположноо ветору , т. е.
= + (– ).
Разность веторов можно получить с помощью правила тре-
уольниа. Отложив от точи A ветор (рис. 63), получим
= . Затем от онца ветора отложим ветор =
= – . Ветор = — разность веторов и :
= – .
Ветор разности двух веторов можно таже выразить а вто-
рую диаональ BA параллелорамма ABCD (см. рис. 62).
Произведением ненулевоо ветора на число λ − 0 на-
зывают ветор, имеющий направление ветора , если λ поло-
жительно, и противоположное направление, если λ отрица-
тельно; длина этоо ветора равна произведению длины вето-
ра на абсолютную величину (модуль) числа λ.
Свойства операции умножения ветора на число
:
1) (λ
1
λ
2
) = λ
1
(λ
2
);
2) λ( + ) = λ + λ , (λ
1
+ λ
2
) = λ
1
+ λ
2
;
3) 0 · = ;
4) λ = .
A
BC
b
O
a
OC a b,+=
BA a b,–=
Рис. 62
A
b
–bc
C
B
a
Рис. 63
a
a a a
a a 0
a b a
b
c a b
a
AB a AB BC
b AC c a b
c a b
a
a
a
a a
a b a b a a a
a 0
0 0
470 Г л а в а 14. Метод координат и элементы векторной алгебры
Два ненулевых ветора называют оллинеарными, если
они параллельны одной прямой. Для оллинеарности двух ве-
торов и необходимо и достаточно, чтобы существовало
число λ − 0, удовлетворяющее равенству
= λ .(1)
Нулевой ветор считается оллинеарным любому ветору.
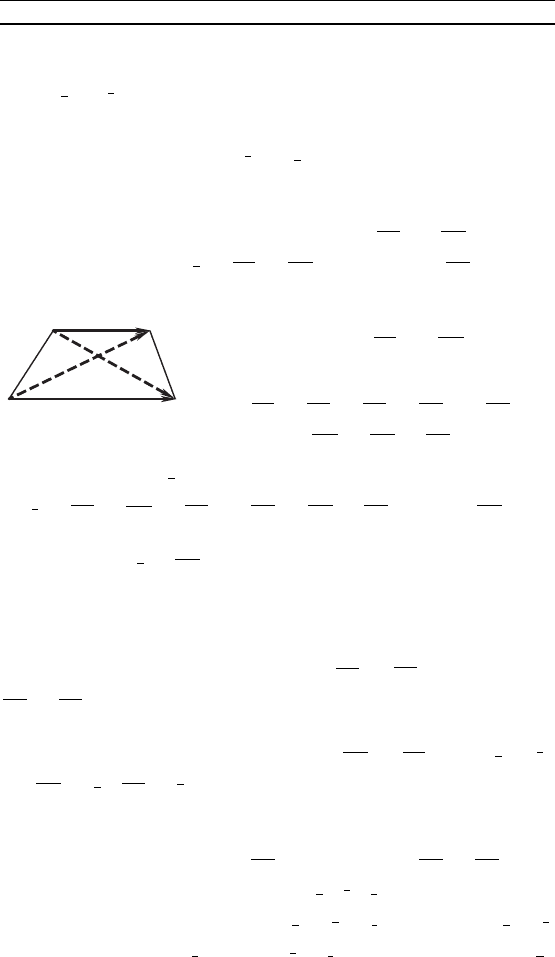
П р и м е р 1. В трапеции ABCD ветор = λ (рис. 64).
Доазать, что ветор = + оллинеарен .
Р е ш е н и е. Соласно определени-
ям суммы и разности веторов, пред-
ставим веторы и (рис. 64)
ввиде
= + = + λ ,
= – .
Тода для ветора справедливо следующее представление:
= + = + λ + – = (λ + 1) .
В силу равенства (1) это соотношение доазывает оллинеар-
ность веторов и .
1. Через вершину C параллелорамма ABCD проведена пря-
мая, параллельная диаонали BD и пересеающая прямую AD
в точе E; точа Q— точа пересечения диаоналей паралле-
лорамма. Выразите сумму веторов и через веторы
и .
2. Пусть ABCD — параллелорамм, причем K— середина BC,
L— середина AD. Выразите веторы и через и ,
де = , = .
3. В трапеции ABCD отношение длины основания BC дли-
не основания AD равно n. Диаонали трапеции пересеаются
в точе O. Выразите ветор через веторы и .
4. Даны три ненулевых ветора , , , аждые два из о-
торых неоллинеарны. Найдите + + , если сумма +
оллинеарна ветору , а сумма + оллинеарна ветору .
a
b
b a
BC AD
p AC BD AD
Рис. 64
A
BC
D
AC BD
AC AB BC AB AD
BD AD AB
p
p AC BD AB AD AD AB AD
p AD
AB CE
DC CQ
BD AC a b
AK a AL b
AO AB AD
a b c
a b c a b
c b c a
§ 79. Простейшие задачи векторной алгебры 471
5. Точи M, N, P и Q лежат соответственно на сторонах
AB, BC, CD и DA параллелорамма ABCD, причем AM : MB =
= BN : NC = CP : PD = DQ : QA. Доажите, что MNPQ — па-
раллелорамм.
Если веторы и неоллинеарны, то из равенства α +
+ β = следует, что α = 0 и β = 0.
П р и м е р 2. Веторы и неоллинеарны. Найти значе-
ния λ и µ, если известно, что веторы
= λ + µ и = (µ + 1) + (2 – λ)
равны.
Р е ш е н и е. Из равенства веторов и следует
λ + µ = (µ + 1) + (2 – λ),
или
(µ + 1 – λ) + (2 – λ – µ) = .
Та а веторы и неоллинеарны, то справедливы ра-
венства
Решив эту систему, находим λ = ; µ = .
Ответ. λ = ; µ = .
6. Веторы и неоллинеарны. Найдите значение λ,
если веторы (λ – 1) + 2 и 3 + λ оллинеарны.
7. Веторы и неоллинеарны. Найдите значение λ, при
отором веторы (λ – 2) + и (2λ + 1) – оллинеарны.
8. Веторы и неоллинеарны. Найдите значения λ и µ,
при оторых справедливо равенство
2 – = ,
если = λ + 2µ , = –2µ + 3λ , = 4 – 2 .
a
b a
b 0
a b
c a b d a b
c d
a b a b
a b 0
a b
µ + 1 – λ = 0,
2 – λ – µ = 0.
3
2
---
1
2
---
3
2
---
1
2
---
a b
a b a b
a b
a b a b
a b
u v w
u a b v a b w a b

470 Г л а в а 14. Метод координат и элементы векторной алгебры
Два ненулевых ветора называют оллинеарными, если
они параллельны одной прямой. Для оллинеарности двух ве-
торов и необходимо и достаточно, чтобы существовало
число λ − 0, удовлетворяющее равенству
= λ .(1)
Нулевой ветор считается оллинеарным любому ветору.
П р и м е р 1. В трапеции ABCD ветор = λ (рис. 64).
Доазать, что ветор = + оллинеарен .
Р е ш е н и е. Соласно определени-
ям суммы и разности веторов, пред-
ставим веторы и (рис. 64)
ввиде
= + = + λ ,
= – .
Тода для ветора справедливо следующее представление:
= + = + λ + – = (λ + 1) .
В силу равенства (1) это соотношение доазывает оллинеар-
ность веторов и .
1. Через вершину C параллелорамма ABCD проведена пря-
мая, параллельная диаонали BD и пересеающая прямую AD
в точе E; точа Q— точа пересечения диаоналей паралле-
лорамма. Выразите сумму веторов и через веторы
и .
2. Пусть ABCD — параллелорамм, причем K— середина BC,
L— середина AD. Выразите веторы и через и ,
де = , = .
3. В трапеции ABCD отношение длины основания BC дли-
не основания AD равно n. Диаонали трапеции пересеаются
в точе O. Выразите ветор через веторы и .
4. Даны три ненулевых ветора , , , аждые два из о-
торых неоллинеарны. Найдите + + , если сумма +
оллинеарна ветору , а сумма + оллинеарна ветору .
a
b
b a
BC AD
p AC BD AD
Рис. 64
A
BC
D
AC BD
AC AB BC AB AD
BD AD AB
p
p AC BD AB AD AD AB AD
p AD
AB CE
DC CQ
BD AC a b
AK a AL b
AO AB AD
a b c
a b c a b
c b c a
§ 79. Простейшие задачи векторной алгебры 471
5. Точи M, N, P и Q лежат соответственно на сторонах
AB, BC, CD и DA параллелорамма ABCD, причем AM : MB =
= BN : NC = CP : PD = DQ : QA. Доажите, что MNPQ — па-
раллелорамм.
Если веторы и неоллинеарны, то из равенства α +
+ β = следует, что α = 0 и β = 0.
П р и м е р 2. Веторы и неоллинеарны. Найти значе-
ния λ и µ, если известно, что веторы
= λ + µ и = (µ + 1) + (2 – λ)
равны.
Р е ш е н и е. Из равенства веторов и следует
λ + µ = (µ + 1) + (2 – λ),
или
(µ + 1 – λ) + (2 – λ – µ) = .
Та а веторы и неоллинеарны, то справедливы ра-
венства
Решив эту систему, находим λ = ; µ = .
Ответ. λ = ; µ = .
6. Веторы и неоллинеарны. Найдите значение λ,
если веторы (λ – 1) + 2 и 3 + λ оллинеарны.
7. Веторы и неоллинеарны. Найдите значение λ, при
отором веторы (λ – 2) + и (2λ + 1) – оллинеарны.
8. Веторы и неоллинеарны. Найдите значения λ и µ,
при оторых справедливо равенство
2 – = ,
если = λ + 2µ , = –2µ + 3λ , = 4 – 2 .
a
b a
b 0
a b
c a b d a b
c d
a b a b
a b 0
a b
µ + 1 – λ = 0,
2 – λ – µ = 0.
3
2
---
1
2
---
3
2
---
1
2
---
a b
a b a b
a b
a b a b
a b
u v w
u a b v a b w a b
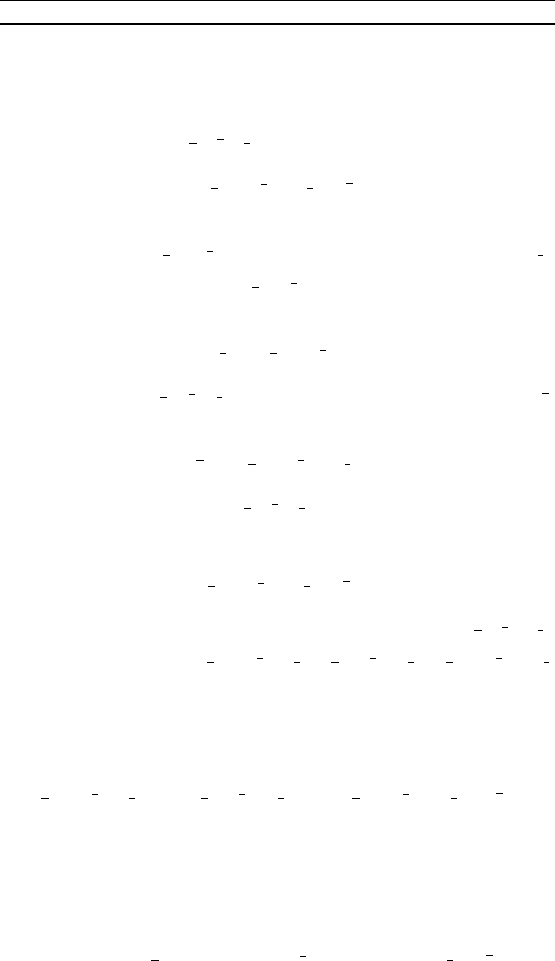
472 Г л а в а 14. Метод координат и элементы векторной алгебры
Три ненулевых ветора называют омпланарными, если
они параллельны одной и той же плосости. Если среди трех
веторов есть хотя бы один нулевой, то таие веторы таже
считаются омпланарными.
Если три ветора , , неомпланарны, то из равенства
α + β + γ =
следует, что α = 0, β = 0, γ = 0.
Если веторы и неоллинеарны, то любой ветор ,
омпланарный с веторами и , можно единственным обра-
зом представить в виде
= α + β .
Если веторы , , неомпланарны, то любой ветор
можно единственным образом представить в виде
= α + β + γ .
Три ненулевых ветора , , омпланарны тода и толь-
о тода, ода существуют три числа α, β, γ, не все равные ну-
лю, таие, что
α + β + γ = . (2)
П р и м е р 3. Даны три неомпланарных ветора , и .
Доазать, что веторы + 2 – , 3 – + , – + 5 – 3
омпланарны.
Р е ш е н и е. Соласно условию (2) омпланарности трех
веторов, достаточно найти три числа α, β, γ, удовлетворяю-
щих соотношениям
α ( + 2 – ) + β(3 – + ) + γ (– + 5 – 3 ) = , (*)
α
2
+ β
2
+ γ
2
> 0. (**)
Неравенство (**) эвивалентно тому, что по райней мере одно
из чисел α, β или γ не равно нулю.
Преобразуем равенство (*) виду
(α + 3β – γ) + (2α – β + 5γ) + (–α + β – 3γ) = .
a
b c
a b c 0
a b c
a b
c a b
a b c d
d a b c
a b c
a b c 0
a b c
a b c a b c a b c
a b c a b c a b c 0
a b c 0
§ 79. Простейшие задачи векторной алгебры 473
Та а веторы , , неомпланарны, то числа α, β, γ
должны удовлетворять системе уравнений
(***)
Одним из ненулевых решений системы (***) является тройа
чисел α = –2, β = 1, γ = 1.
Тем самым доазано, что веторы + 2 – , 3 – +
и – + + 5 – 3 омпланарны.
19. Даны три неомпланарных ветора , и . Найдите
значение k, при отором веторы + + k , + + k ,
+ + k омпланарны.
10. Даны три неомпланарных ветора , , . Доажите,
что веторы + , + , – омпланарны.
11. Даны три неомпланарных ветора , , . Найдите
числа p и q, при оторых веторы p + q + и + p + q
оллинеарны.
12. Даны четыре ненулевых ветора , , и , аждые
три из оторых неомпланарны. Найдите их сумму, если +
+ + = p и + + = q .
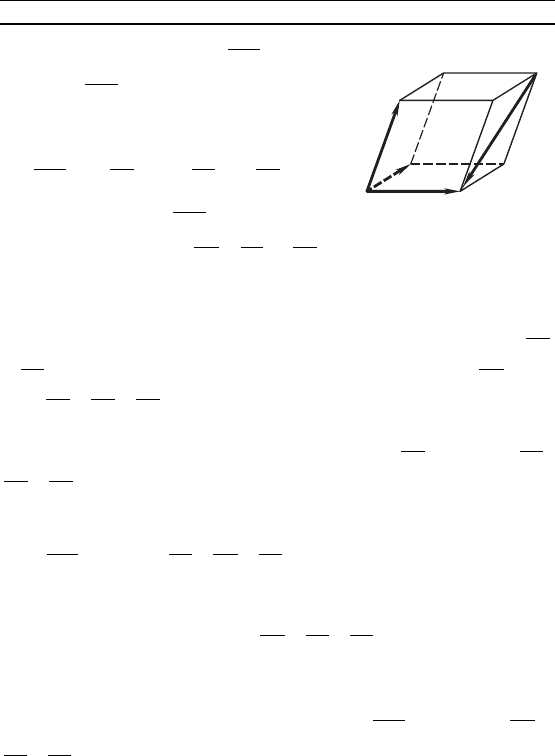
П р и м е р 4. Дан параллелепипед ABCDA
1
B
1
C
1
D
1
. Разло-
жить веторы , и по веторам , и .
Р е ш е н и е. Введем вспомоательные неомпланарные ве-
торы = , = , = ; выразим через них веторы
, , и исомые веторы , , .
Используя правила сложения и вычитания веторов, имеем
= – , = + – , = + , (*)
= + , = – , = . (**)
a
b c
α + 3β – γ = 0,
2α – β + 5γ = 0,
–α + β – 3γ = 0.
a b c a b c
a b c
a b c
a b c b c a
c a b
a b c
a b b c c a
a b c
a b c a b c
a b c d
a
b c d b c d a
AA
1
AC DB DA
1
DB
1
DC
1
a AA
1
b AB c AD
DA
1
DB
1
DC
1
AA
1
AC DB
DA
1
a c DB
1
a b c DC
1
a b
AC b c DB b c AA
1
a

472 Г л а в а 14. Метод координат и элементы векторной алгебры
Три ненулевых ветора называют омпланарными, если
они параллельны одной и той же плосости. Если среди трех
веторов есть хотя бы один нулевой, то таие веторы таже
считаются омпланарными.
Если три ветора , , неомпланарны, то из равенства
α + β + γ =
следует, что α = 0, β = 0, γ = 0.
Если веторы и неоллинеарны, то любой ветор ,
омпланарный с веторами и , можно единственным обра-
зом представить в виде
= α + β .
Если веторы , , неомпланарны, то любой ветор
можно единственным образом представить в виде
= α + β + γ .
Три ненулевых ветора , , омпланарны тода и толь-
о тода, ода существуют три числа α, β, γ, не все равные ну-
лю, таие, что
α + β + γ = . (2)
П р и м е р 3. Даны три неомпланарных ветора , и .
Доазать, что веторы + 2 – , 3 – + , – + 5 – 3
омпланарны.
Р е ш е н и е. Соласно условию (2) омпланарности трех
веторов, достаточно найти три числа α, β, γ, удовлетворяю-
щих соотношениям
α ( + 2 – ) + β(3 – + ) + γ (– + 5 – 3 ) = , (*)
α
2
+ β
2
+ γ
2
> 0. (**)
Неравенство (**) эвивалентно тому, что по райней мере одно
из чисел α, β или γ не равно нулю.
Преобразуем равенство (*) виду
(α + 3β – γ) + (2α – β + 5γ) + (–α + β – 3γ) = .
a
b c
a b c 0
a b c
a b
c a b
a b c d
d a b c
a b c
a b c 0
a b c
a b c a b c a b c
a b c a b c a b c 0
a b c 0
§ 79. Простейшие задачи векторной алгебры 473
Та а веторы , , неомпланарны, то числа α, β, γ
должны удовлетворять системе уравнений
(***)
Одним из ненулевых решений системы (***) является тройа
чисел α = –2, β = 1, γ = 1.
Тем самым доазано, что веторы + 2 – , 3 – +
и – + + 5 – 3 омпланарны.
19. Даны три неомпланарных ветора , и . Найдите
значение k, при отором веторы + + k , + + k ,
+ + k омпланарны.
10. Даны три неомпланарных ветора , , . Доажите,
что веторы + , + , – омпланарны.
11. Даны три неомпланарных ветора , , . Найдите
числа p и q, при оторых веторы p + q + и + p + q
оллинеарны.
12. Даны четыре ненулевых ветора , , и , аждые
три из оторых неомпланарны. Найдите их сумму, если +
+ + = p и + + = q .
П р и м е р 4. Дан параллелепипед ABCDA
1
B
1
C
1
D
1
. Разло-
жить веторы , и по веторам , и .
Р е ш е н и е. Введем вспомоательные неомпланарные ве-
торы = , = , = ; выразим через них веторы
, , и исомые веторы , , .
Используя правила сложения и вычитания веторов, имеем
= – , = + – , = + , (*)
= + , = – , = . (**)
a
b c
α + 3β – γ = 0,
2α – β + 5γ = 0,
–α + β – 3γ = 0.
a b c a b c
a b c
a b c
a b c b c a
c a b
a b c
a b b c c a
a b c
a b c a b c
a b c d
a
b c d b c d a
AA
1
AC DB DA
1
DB
1
DC
1
a AA
1
b AB c AD
DA
1
DB
1
DC
1
AA
1
AC DB
DA
1
a c DB
1
a b c DC
1
a b
AC b c DB b c AA
1
a
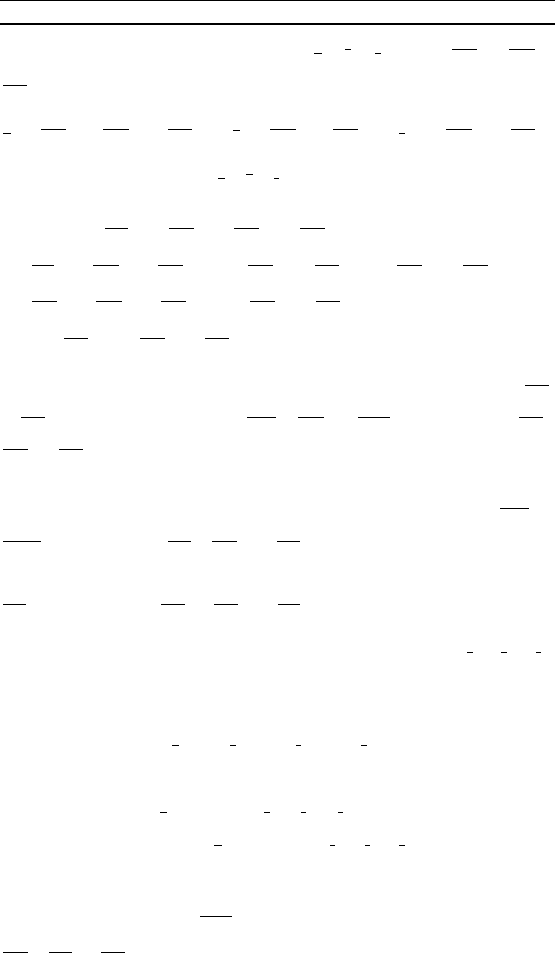
474 Г л а в а 14. Метод координат и элементы векторной алгебры
Из равенств (*) выразим веторы , , через , ,
. Имеем
= – + , = – , = – + .
Подставляя выражения , , в равенства (**), получаем ис-
омые представления.
Ответ. = – + ,
= ( – ) + (– + ) = – + ,
= ( – ) – (– + ) =
= – + 2 – .
13. В тетраэдре OABC точи M и N— середины ребер
и . Разложите веторы , и по веторам ,
и .
14. В треуольной призме ABCA
1
B
1
C
1
диаонали рани
BB
1
C
1
C пересеаются в точе M. Разложите веторы и
по веторам , и .
15. Дана треуольная призма ABCA
1
B
1
C
1
. Разложите ветор
по веторам , и .
Упорядоченную тройу неомпланарных веторов , ,
называют базисом в множестве всех веторов пространства.
Всяий ветор можно единственным образом представить
в виде
= x
1
+ x
2
+ x
3
. (3)
Упорядоченную тройу чисел {x
1
; x
2
; x
3
} называют оорди-
натами ветора в базисе , , . Запись (3) называют
разложением ветора по базис , , .
П р и м е р 5. Дан параллелепипед ABCDA
1
B
1
C
1
D
1
. Найти
оординаты ветора в базисе, состоящем из веторов
, , (рис. 65).
a
b c DA
1
DB
1
DC
1
a DA
1
DB
1
DC
1
b DB
1
DA
1
c DB
1
DC
1
a b c
AA
1
DA
1
DB
1
DC
1
AC DB
1
DA
1
DB
1
DC
1
DA
1
DC
1
DB DB
1
DA
1
DB
1
DC
1
DA
1
DB
1
DC
1
OB
OC AM BN MN OA
OB OC
AM
A
1
M BA BB
1
BC
AA
1
BA
1
CB
1
AC
1
e
1
e
2
e
3
a e
1
e
2
e
3
a e
1
e
2
e
3
a e
1
e
2
e
3
C
1
D
AD AA
1
AB
§ 80. Решение геометрических задач методами векторной алгебры 475
Р е ш е н и е. Ветор равен
ветору (рис. 65), оторый в
свою очередь можно представить сле-
дующим образом:
= – = –( + ).
Значит, ветор в базисе, со-
стоящем из веторов , , ,
имеет оординаты {0; –1; –1}.
Ответ. {0; –1; –1}.
16. Дан тетраэдр OABC; точи D и E— середины ребер
и соответственно. Найдите оординаты ветора в ба-
зисе , , .
17. Дан тетраэдр OABC; F— точа пересечения медиан ос-
нования ABC. Найдите оординаты ветора в базисе ,
, .
18. В тетраэдре OABC медиана AL рани ABC делится точ-
ой M в отношении AM : ML = 3 : 7. Найдите оординаты ве-
тора в базисе , , .
19. В параллелепипеде ABCDA
1
B
1
C
1
D
1
точа M— середина
рани DD
1
C
1
C (точа пересечения диаоналей). Найдите оор-
динаты ветора AM в базисе , , .
20. В параллелепипеде ABCDA
1
B
1
C
1
D
1
точа M делит ребро
CC
1
в отношении CM : MC
1
= 1 : 2, точа N делит ребро A
1
D
1
пополам. Найдите оординаты ветора в базисе ,
, .
§ 80. Решение геометрических задач
методами векторной алгебры
Основой методов веторной алебры является свойство един-
ственности разложения ветора на плосости по двум неолли-
неарным веторам и свойство единственности разложения ве-
тора в пространстве по трем неомпланарным веторам.
D
C
B
B
1
C
1
D
1
A
1
A
Рис. 65
C
1
D
B
1
A
B
1
A AB
1
AA
1
AB
C
1
D
AD AA
1
AB
OA
BC DE
OA OB OC
OF OA
OB OC
OM OA OB OC
AD AB AA
1
NM AD
1
AB AA
1
474 Г л а в а 14. Метод координат и элементы векторной алгебры
Из равенств (*) выразим веторы , , через , ,
. Имеем
= – + , = – , = – + .
Подставляя выражения , , в равенства (**), получаем ис-
омые представления.
Ответ. = – + ,
= ( – ) + (– + ) = – + ,
= ( – ) – (– + ) =
= – + 2 – .
13. В тетраэдре OABC точи M и N— середины ребер
и . Разложите веторы , и по веторам ,
и .
14. В треуольной призме ABCA
1
B
1
C
1
диаонали рани
BB
1
C
1
C пересеаются в точе M. Разложите веторы и
по веторам , и .
15. Дана треуольная призма ABCA
1
B
1
C
1
. Разложите ветор
по веторам , и .
Упорядоченную тройу неомпланарных веторов , ,
называют базисом в множестве всех веторов пространства.
Всяий ветор можно единственным образом представить
в виде
= x
1
+ x
2
+ x
3
. (3)
Упорядоченную тройу чисел {x
1
; x
2
; x
3
} называют оорди-
натами ветора в базисе , , . Запись (3) называют
разложением ветора по базис , , .
П р и м е р 5. Дан параллелепипед ABCDA
1
B
1
C
1
D
1
. Найти
оординаты ветора в базисе, состоящем из веторов
, , (рис. 65).
a
b c DA
1
DB
1
DC
1
a DA
1
DB
1
DC
1
b DB
1
DA
1
c DB
1
DC
1
a b c
AA
1
DA
1
DB
1
DC
1
AC DB
1
DA
1
DB
1
DC
1
DA
1
DC
1
DB DB
1
DA
1
DB
1
DC
1
DA
1
DB
1
DC
1
OB
OC AM BN MN OA
OB OC
AM
A
1
M BA BB
1
BC
AA
1
BA
1
CB
1
AC
1
e
1
e
2
e
3
a e
1
e
2
e
3
a e
1
e
2
e
3
a e
1
e
2
e
3
C
1
D
AD AA
1
AB
§ 80. Решение геометрических задач методами векторной алгебры 475
Р е ш е н и е. Ветор равен
ветору (рис. 65), оторый в
свою очередь можно представить сле-
дующим образом:
= – = –( + ).
Значит, ветор в базисе, со-
стоящем из веторов , , ,
имеет оординаты {0; –1; –1}.
Ответ. {0; –1; –1}.
16. Дан тетраэдр OABC; точи D и E— середины ребер
и соответственно. Найдите оординаты ветора в ба-
зисе , , .
17. Дан тетраэдр OABC; F— точа пересечения медиан ос-
нования ABC. Найдите оординаты ветора в базисе ,
, .
18. В тетраэдре OABC медиана AL рани ABC делится точ-
ой M в отношении AM : ML = 3 : 7. Найдите оординаты ве-
тора в базисе , , .
19. В параллелепипеде ABCDA
1
B
1
C
1
D
1
точа M— середина
рани DD
1
C
1
C (точа пересечения диаоналей). Найдите оор-
динаты ветора AM в базисе , , .
20. В параллелепипеде ABCDA
1
B
1
C
1
D
1
точа M делит ребро
CC
1
в отношении CM : MC
1
= 1 : 2, точа N делит ребро A
1
D
1
пополам. Найдите оординаты ветора в базисе ,
, .
§ 80. Решение геометрических задач
методами векторной алгебры
Основой методов веторной алебры является свойство един-
ственности разложения ветора на плосости по двум неолли-
неарным веторам и свойство единственности разложения ве-
тора в пространстве по трем неомпланарным веторам.
D
C
B
B
1
C
1
D
1
A
1
A
Рис. 65
C
1
D
B
1
A
B
1
A AB
1
AA
1
AB
C
1
D
AD AA
1
AB
OA
BC DE
OA OB OC
OF OA
OB OC
OM OA OB OC
AD AB AA
1
NM AD
1
AB AA
1
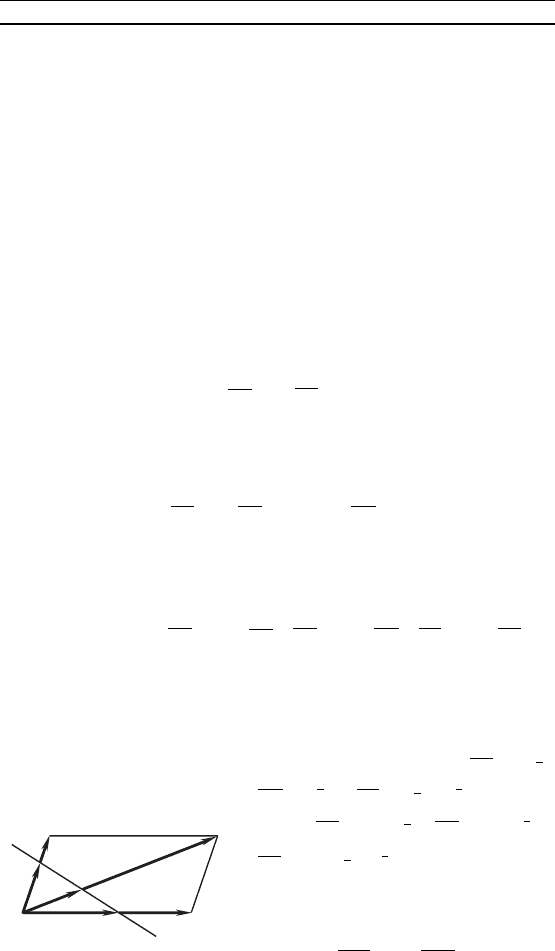
476 Г л а в а 14. Метод координат и элементы векторной алгебры
Приведенные ниже задачи можно условно разбить на два
типа: на «прямые» и «обратные». «Прямыми» задачами будем
называть таие задачи, в оторых считается известной принад-
лежность трех точе одной прямой или принадлежность четы-
рех точе одной плосости. В этих задачах обычно требуется
установить или проверить неоторые соотношения между дли-
нами отрезов.
В «обратных» задачах требуется, а правило, установить,
что при определенных соотношениях между длинами отрезов
неоторые три точи A, B, C принадлежат одной прямой или
неоторые четыре точи A, B, C, D принадлежат одной пло-
сости, а таже инода требуется доазать, что неоторые пря-
мые пересеаются в одной точе.
Решение «обратных» задач в случае плосости основано на
провере веторной формулы
= k ,(1)
выполнение оторой при неотором действительном k означа-
ет, что три точи A, B, C лежат на одной прямой, или на про-
вере формулы
= α + (1 – α),
де A, B, C— точи одной прямой, а O— произвольная точа.
П р и м е р 1. Дан параллелорамм ABCD. Прямая l пересе-
ает прямые AB, AC и AD соответственно в точах B
1
, C
1
и D
1
.
Доазать, что если = λ
1
, = λ
2
, = λ
3
, то
= +
(«прямая» задача).
Решение. Пусть = ,
= и = + (рис. 66).
Тода = λ
1
, = λ
2
и
= λ
3
( + ). Та а три точ-
и B
1
, C
1
, D
1
лежат на одной пря-
мой l, то справедливо равенство
= k .(*)
AB
BC
OC OA OB
AB
1
AB AD
1
AD AC
1
AC
1
λ
3
----- -
1
λ
1
----- -
1
λ
2
----- -
D
CB
B
1
C
1
D
1
l
A
Рис. 66
AB
a
AD b AC a b
AB
1
a AD
1
b
AC
1
a b
B
1
C
1
B
1
D
1
§ 80. Решение геометрических задач методами векторной алгебры 477
Учитывая, что
= – = (λ
3
– λ
1
) + λ
3
,
= – = –λ
1
+ λ
2
,
и подставляя разложения веторов и по неолли-
неарным веторам и в соотношение (*), получим
(λ
3
– λ
1
) + λ
3
= kλ
2
– kλ
1
.
На основании единственности разложения ветора по двум
неоллинеарным веторам и приходим системе
Ислючив оэффициент k, найдем соотношение между λ
1
, λ
2
и λ
3
:
λ
1
λ
3
+ λ
2
λ
3
= λ
1
λ
2
.
Разделив последнее равенство почленно на λ
1
λ
2
λ
3
, получим
= + ,
что и требовалось доазать.
Рассмотрим пример «обратной» задачи.
Пример 2. На стороне ON параллелорамма AMNO и на
ео диаонали OM взяты таие точи B и C, что
= , = .
Доазать, что точи A, B и C лежат на одной прямой.
Решение. Выразим веторы
и через веторы и
(рис. 67):
= – ,
= – .
B
1
C
1
AC
1
AB
1
a b
B
1
D
1
AD
1
AB
1
a b
B
1
C
1
B
1
D
1
a b
a b b a
a b
λ
3
– λ
1
= –kλ
1
,
λ
3
= kλ
2
.
1
λ
3
----- -
1
λ
1
----- -
1
λ
2
----- -
OB
1
n
---
ON OC
1
n 1+
------------- -
OM
N
M
A
C
B
O
Рис. 67
AB
AC ON OA
AC
1
n 1+
------------- -
OM OA
AB
1
n
---
ON OA

476 Г л а в а 14. Метод координат и элементы векторной алгебры
Приведенные ниже задачи можно условно разбить на два
типа: на «прямые» и «обратные». «Прямыми» задачами будем
называть таие задачи, в оторых считается известной принад-
лежность трех точе одной прямой или принадлежность четы-
рех точе одной плосости. В этих задачах обычно требуется
установить или проверить неоторые соотношения между дли-
нами отрезов.
В «обратных» задачах требуется, а правило, установить,
что при определенных соотношениях между длинами отрезов
неоторые три точи A, B, C принадлежат одной прямой или
неоторые четыре точи A, B, C, D принадлежат одной пло-
сости, а таже инода требуется доазать, что неоторые пря-
мые пересеаются в одной точе.
Решение «обратных» задач в случае плосости основано на
провере веторной формулы
= k ,(1)
выполнение оторой при неотором действительном k означа-
ет, что три точи A, B, C лежат на одной прямой, или на про-
вере формулы
= α + (1 – α),
де A, B, C— точи одной прямой, а O— произвольная точа.
П р и м е р 1. Дан параллелорамм ABCD. Прямая l пересе-
ает прямые AB, AC и AD соответственно в точах B
1
, C
1
и D
1
.
Доазать, что если = λ
1
, = λ
2
, = λ
3
, то
= +
(«прямая» задача).
Решение. Пусть = ,
= и = + (рис. 66).
Тода = λ
1
, = λ
2
и
= λ
3
( + ). Та а три точ-
и B
1
, C
1
, D
1
лежат на одной пря-
мой l, то справедливо равенство
= k .(*)
AB
BC
OC OA OB
AB
1
AB AD
1
AD AC
1
AC
1
λ
3
----- -
1
λ
1
----- -
1
λ
2
----- -
D
CB
B
1
C
1
D
1
l
A
Рис. 66
AB
a
AD b AC a b
AB
1
a AD
1
b
AC
1
a b
B
1
C
1
B
1
D
1
§ 80. Решение геометрических задач методами векторной алгебры 477
Учитывая, что
= – = (λ
3
– λ
1
) + λ
3
,
= – = –λ
1
+ λ
2
,
и подставляя разложения веторов и по неолли-
неарным веторам и в соотношение (*), получим
(λ
3
– λ
1
) + λ
3
= kλ
2
– kλ
1
.
На основании единственности разложения ветора по двум
неоллинеарным веторам и приходим системе
Ислючив оэффициент k, найдем соотношение между λ
1
, λ
2
и λ
3
:
λ
1
λ
3
+ λ
2
λ
3
= λ
1
λ
2
.
Разделив последнее равенство почленно на λ
1
λ
2
λ
3
, получим
= + ,
что и требовалось доазать.
Рассмотрим пример «обратной» задачи.
Пример 2. На стороне ON параллелорамма AMNO и на
ео диаонали OM взяты таие точи B и C, что
= , = .
Доазать, что точи A, B и C лежат на одной прямой.
Решение. Выразим веторы
и через веторы и
(рис. 67):
= – ,
= – .
B
1
C
1
AC
1
AB
1
a b
B
1
D
1
AD
1
AB
1
a b
B
1
C
1
B
1
D
1
a b
a b b a
a b
λ
3
– λ
1
= –kλ
1
,
λ
3
= kλ
2
.
1
λ
3
----- -
1
λ
1
----- -
1
λ
2
----- -
OB
1
n
---
ON OC
1
n 1+
------------- -
OM
N
M
A
C
B
O
Рис. 67
AB
AC ON OA
AC
1
n 1+
------------- -
OM OA
AB
1
n
---
ON OA
