Dantzig G., Thapa M. Linear programming. Vol.1. Introduction

Подождите немного. Документ загружается.

132 DUALITY

Primal

Variables x

≥ 0 x

≤ 0 x

Relation Constants

1 −34= 5

≥ 0 1 −2 ≥ 3

Dual y

≤ 0 2 −1 ≤ 4

Relation ≤≥= ≤

Max v

Constants 111≥ Min z

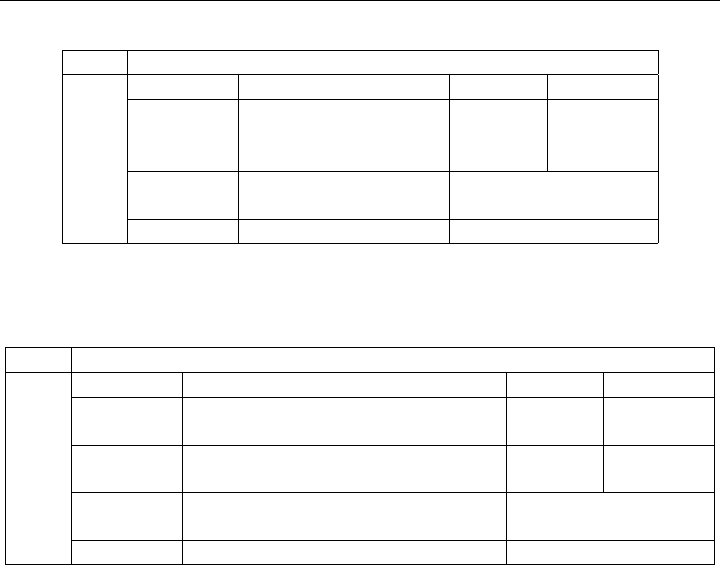
Table 5-3: Example of a Dual of a Mixed System

Primal

Variables

≥ 0 x



≥ 0 x



≥ 0 x



≥ 0 Relation Constants



≥ 0 134−4 ≥ 5



≥ 0 −1 −3 −44≥ −5

Dual y

≥ 0 12 ≥ 3

−y

≥ 0 21−1 ≥ −4

Relation ≤≤≤≤ ≤

Max v

Constants 1 −11−1 ≥ Min z

Table 5-4: Example of a Dual of a Mixed System (Continued)

5.1.4 THE DUAL OF THE STANDARD FORM

Applying the correspondence rules of Table 5-2, the dual of the standard form

is easily obtained; see Table 5-5. The dual variables, which in this case are all

unrestricted in sign, are denoted by π

(instead of y

) to conform with the notation

used in earlier chapters (See Equation 1.8).

Thus, the primal problem for the standard linear program given in Table 5-5 is

Minimize c

x = z

subject to Ax = b, A : m × n,

x ≥ 0,

(5.5)

and the dual problem for the standard linear program is to

Maximize b

π = v

subject to A

π ≤ c, A : m × n,

(5.6)

where π

is unrestricted in sign.

5.2 DUALITY THEOREMS 133

Primal

Variables x

≥ 0 x

≥ 0 ··· x

≥ 0 Relation Constants

··· a

= b

··· a

= b

Dual

. (Dual Obj)

··· a

= b

Relation ≤ ≤ ··· ≤ ≤

Max v

Constants c

··· c

≥ Min z

(Primal Objective)

Table 5-5: Primal/Dual System for Standard Form

 Exercise 5.2 Show that the dual of a dual of a primal linear program in standard form

is itself the primal linear program in standard form.

5.1.5 PRIMAL-DUAL FEASIBLE-INFEASIBLE CASES

All four combinations of feasibility and infeasibility of the primal and dual systems

are possible as shown in the examples below:

Example 5.2 (Primal Feasible, Dual Feasible, and Min z = Max v)

Primal:

= z (Min)

≥ 0

Dual:

5π

= v (Max)

≤ 1

Example 5.3 (Primal Feasible, Dual Infeasible, and Min z →−∞)

Primal:

−x

− x

= z (Min)

− x

≥ 0,x

≥ 0

Dual:

5π

= v (Max)

≤−1

−π

≤−1

Example 5.4 (Primal Infeasible, Dual Feasible, and Max v →∞)

Primal:

= z (Min)

= −5

≥ 0

Dual:

−5π

= v (Max)

≤ 1

Example 5.5 (Primal Infeasible, Dual Infeasible)

Primal:

−x

− x

= z (Min)

− x

=+5

− x

= −5

≥ 0,x

≥ 0

Dual:

5π

− 5π

= v (Max)

+ π

≤−1

−π

− π

≤−1

 Exercise 5.3 Verify the above four examples.

134 DUALITY

5.2 DUALITY THEOREMS

The Duality Theorem is a statement about the range of possible z values for the

primal versus the range of possible v values for the dual. This is depicted graphically

in Figure 5-1 for the case where the primal and dual are both feasible.

Von Neumann stated but did not prove the Duality Theorem: If the primal (5.1)

and dual (5.2) as stated above have feasible solutions, then there exist optimal feasible

solutions to both the primal and the dual that are equal. Here we simply state and

illustrate the Strong Duality Theorem and the Weak Duality Theorem.

Assuming that primal and dual solutions exist, the weaker form of the Duality

Theorem is

THEOREM 5.1 (Weak Duality Theorem) If x

is any feasible solution to

the primal (5.1) and y

is any feasible solution to the dual (5.2), then

b = v

≤ z

= c

. (5.7)

Example 5.6 (Illustration of Weak Duality) Consider the primal problem

+3x

= z (min)

+3x

≥−2

+4x

≥−2

≥ 0,x

≥ 0

(5.8)

and its dual

−2y

− 2y

= v (max)

+2y

≤ 5

+4y

≤ 3

≥ 0,y

≥ 0.

(5.9)

A feasible solution to the primal problem is x

=1,x

= 1, with z = 8. A feasible solution

to the dual is y

=0.1, y

=0.1, with v = −0.4. As expected, according to the Weak

Duality Theorem, we have −0.4=v ≤ z =8.

Note: The bounds on the objective values are for any pair of feasible solutions.

When the Simplex Method is used to solve a linear program, each iteration in

Phase II ensures primal feasibility but not dual feasibility. In fact when dual fea-

sibility is attained, an optimal solution is obtained. In the intermediate steps of

Phase II, however, the primal and dual objectives are equal to each other, because

v = π

b = π

Bx = c

= z, where π is dual infeasible

COROLLARY 5.2 (Bounds on the Objectives) Every feasible solution y

to the dual yields a lower bound y

b to values of z

for feasible solutions x

to the

primal. Conversely, every feasible solution x

to the primal yields an upper bound

to values of v

for feasible solutions y

to the dual.

5.3 COMPLEMENTARY SLACKNESS 135

sup v inf zz

 -

Duality Gap

Figure 5-1: Illustration of the Duality Gap

We can depict the relationship by plotting the points v

and z

on a line, as

shown in Figure 5-1.

We are now ready to formally state Von Neumann’s Duality Theorem which in

words states that if feasible solutions to the primal and dual exist then the duality

gap (depicted in Figure 5-1) is zero and that sup v is actually attained for some

choice of y and inf z is attained for some choice of x.

THEOREM 5.3 (Strong Duality Theorem) If the primal system min z =

x, Ax ≥ b, x ≥ 0 has a feasible solution and the dual system max v = b

y ≤ c, y ≥ 0 has a feasible solution, then there exist optimal feasible solutions

x = x

∗

and y = y

∗

to the primal and dual systems such that

∗

= max v = min z = c

∗

. (5.10)

Example 5.7 (Illustration of the Duality Theorem) An optimal solution to the

primal problem (5.8) is x

=0,x

= 0, with z = 0. A optimal solution to the dual (5.9)

is y

=0.0, y

=0.0, with v =0.0. As expected, according to the Duality Theorem, we

have 0.0=v = z =0.0.

5.3 COMPLEMENTARY SLACKNESS

An important property of primal/dual systems is complementary slackness. Let

≥ 0 be any feasible solution satisfying (5.1) and y

≥ 0 be any feasible solution

satisfying (5.2); we assume here that there exist feasible solutions. We rewrite the

former in standard equality form:

Minimize c

x = z

subject to Ax − Ix

= b

x ≥ 0,

(5.11)

where x

=(x

n+1

n+2

,...,x

n+m

)

≥ 0 are variables that measure the extent of

inequality, or negative slack, between the left- and right-hand sides of the inequali-

ties.

136 DUALITY

It will be convenient also to let y

=(y

m+1

m+2

,...,y

m+n

) ≥ 0 measure the

positive slack in the inequalities of the dual system. Then (5.2) in standard equality

form becomes

Maximize b

y = v

subject to A

y + Iy

= c

y ≥ 0,

(5.12)

where y

=(y

m+1

m+2

,...,y

m+n

)

≥ 0.

THEOREM 5.4 (Complementary Slackness) For optimal feasible solutions

of the primal (5.1) and dual (5.2) systems, whenever the kth relation of either system

is slack, the kth variable of its dual is zero; if the kth variable is positive in either

system, the kth relation of its dual is tight, i.e.,

m+k

=0,k=1,...,n, and y

m+k

=0,k=1,...,m. (5.13)

Example 5.8 (Illustration of Complementary Slackness) At the optimal solution

of (5.8), see Example 5.7, we have n =2,m = 2, and

x =(x

)=(0, 0)

=(x

)

=(2, 2)

and

y =(y

)=(0, 0)

=(y

)

=(5, 3)

Clearly

=0,x

=0,y

=0.

 Exercise 5.4 Create an example with at least 3 variables that has an obvious feasible

solution to the primal and an obvious lower bound for z. State the dual. Use the DTZG

Simplex Primal software option to verify the Duality Theorem by solving both systems.

5.4 OBTAINING A DUAL SOLUTION

It turns out that when a primal linear program is solved, the dual solution can

also be obtained very easily. We shall illustrate this through an example of a linear

program in standard form to which a full set of artiﬁcial variables has been added.

Example 5.9 (Dual Solution from an Optimal Tableau) Consider the problem of

Example 3.1: Find min z, x ≥ 0 such that

+1x

+2x

+ x

+4x

= z

+2x

+13x

+3x

+ x

=17

+ x

+5x

+ x

=7.

(5.14)

The optimal tableau for this problem, found in 3 iterations, is displayed in Table 5-6.

Recall from (3.63) in the discussion of the Revised Simplex Method that the reduced costs

corresponding to the artiﬁcial variables are −c

−1

, which are the same as the negative

of the simplex multipliers, or dual variables, π. Hence the dual variables π can be read oﬀ

directly from the optimal simplex tableau, which contains the artiﬁcial variables. In this

case they are π

= −1, π

= −19/2. The optimal dual objective value v = 4 is the same

as the optimal primal objective value z = 4 by the Duality Theorem.

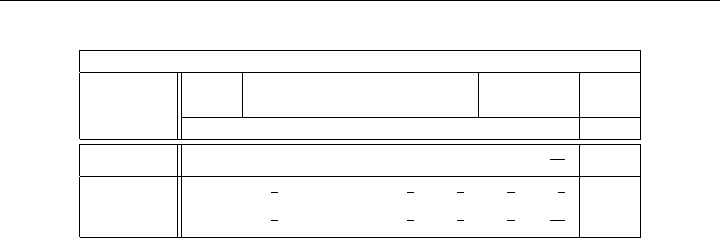
5.5 NOTES & SELECTED BIBLIOGRAPHY 137

Optimal Tableau

Basic OBJ Original Variables Artiﬁcial RHS

Variables Variables

−zx

−z 13 121

−4

−

1 −

−

Table 5-6: Simplex Method: Optimal Tableau

 Exercise 5.5 Explain why π

= −1, π

= −19/2 satisﬁes A

π and hence is a feasible

dual solution. Explain why x

=2,x

=1,x

= x

= 0 is a feasible

primal solution and why we have c

x = b

π.

Another important property for primal/dual systems is

THEOREM 5.5 (Primal/Dual Optimality Criteria) Let (x

∗

,...,x

∗

) be

a feasible solution to a primal linear program in standard form and (π

∗

,...,π

∗

)

be a feasible solution to its dual, satisfying

¯c

∗

= c − A

∗

≥ 0,b

∗

= v

∗

. (5.15)

Then a necessary and suﬃcient condition for optimality of both solutions is

¯c

∗

=0, for x

∗

> 0. (5.16)

Example 5.10 (Illustration of Primal/Dual Optimality) In the optimal tableau

displayed in Table 5-6, we have

¯c

∗







19/2







∗













It is clear that ¯c

∗

= 0 for x

∗

> 0.

138 DUALITY

5.5 NOTES & SELECTED BIBLIOGRAPHY

As noted in this chapter, associated with every linear programming problem is another

linear programming problem called the dual. The fundamental notion of duality and the

term were introduced by John von Neumann (in conversations with George Dantzig in

October 1947) and appear implicitly in a working paper he wrote a few weeks later (von

Neumann [1947]). George Dantzig’s report, A Theorem on Linear Inequalities, dated 5

January 1948, contains the ﬁrst known rigorous (unpublished) proof of the Duality The-

orem. Subsequently Gale, Kuhn, & Tucker [1951] independently formulated the Duality

Theorem, which they proved by means of a classical lemma due to Farkas [1902]. This the-

orem, known as Farkas’s Lemma (see Linear Programming 2), ﬁrst appeared as a lemma

in Farkas’s 1902 paper. A constructive proof of the Duality Theorem using the Simplex

Method can be found in Dantzig [1963]. J. Abadie in verbal communications [1965] with

one of the authors showed how to use the Infeasibility Theorem to prove von Neumann’s

Strong Duality Theorem. We shall formally prove the Duality Theorem in Linear Pro-

gramming 2, using the Infeasibility Theorem 2.3.

It was Tobias Dantzig, mathematician and author, well known for his books popular-

izing the history of mathematics, who suggested around 1955 to his son George the term

primal as the natural antonym to dual since both primal and dual derive from the Latin.

A systematic presentation of theoretical properties of dual linear programs can be

found in Gale [1956] and Goldman & Tucker [1956a,b]. A review of von Neumann’s

contributions can be found in Kuhn & Tucker [1958]. Today everyone cites von Neumann as

the originator of the Duality Theorem and credits Gale, Kuhn, & Tucker as the publishers

of the ﬁrst rigorous proof.

As already noted, there are several important duality-type results, known as “Either

Or” theorems of the alternatives, that predate the linear programming era: Farkas [1902],

Gordan [1873], Motzkin [1936], Stiemke [1915], and Ville [1938]. The earliest known result

on feasibility is one concerning homogeneous systems, Gordan [1873]: “Either a linear

homogeneous system of equations Ax = 0 possesses a nontrivial solution in nonnegative

variables or there exists an equation, formed by taking some linear combination of the

equations, that has all positive coeﬃcients.”

A natural question to ask is why not use the classical method of Lagrange multipliers

to solve the linear programming problem. If we were to do so we would be required to

ﬁnd optimal multipliers (or prices π), which, if they exist, must satisfy a “dual” system

with the property that the ¯c

(or relative cost factors) and optimal x

satisfy ¯c

= 0 for

j =1,...,n. The latter leads to 2

possible cases of either ¯c

=0orx

= 0. It is here that

this classical approach breaks down, for it is not practical to consider all 2

possible cases

for large n. In a certain sense, however, the Simplex Method can be viewed as a systematic

way to eliminate most of these cases and to consider only a few. Indeed, it immediately

restricts the number of cases by considering only those with n − m of the x

= 0 at one

time and such that the coeﬃcient matrix of the remaining m variables is nonsingular;

moreover, the unique value of these variables is positive (under nondegeneracy). The

conditions ¯c

= 0 tell us that ¯c

= 0 for x

> 0 and this determines uniquely π

and the

remaining ¯c

. If it turns out that not all ¯c

≥ 0, the case is dropped and a special new one

is examined on the next iteration, and so on.

5.6 PROBLEMS 139

5.6 PROBLEMS

5.1 Set up the dual of the problem of ﬁnding x

Minimize x

+ x

= z

subject to x

+2x

≥ 3

− 2x

≥−4

+7x

≤ 6,

where x

≥ 0 and x

is unrestricted in sign. Determine the simplex multipliers

of the optimal solution of the primal and verify that it satisﬁes the dual and

gives the same value for the objective form.

5.2 Find the dual of

Minimize x

+2x

+ x

= z

subject to x

+ x

|≤4,x

≥ 0,x

≥ 0.

5.3 Use the DTZG Simplex Primal software option to show that the following linear

program is infeasible.

Minimize −x

− 3x

+5x

+2x

= z

subject to x

+2x

− x

+ x

≤ 4

− x

≥ 8

≥ 0,j=1,...,4.

Write down its dual and use the DTZG Simplex Primal software option to show

that the dual is unbounded.

5.4 Consider the linear program:

Minimize −2x

− x

= z

subject to 2x

− x

≥ 4

≤ 1

≥ 0,x

≥ 0.

(a) Plot the feasible region of the primal and show that it is empty.

(b) Plot the feasible region of its dual and show that a class of solutions exists

for which the dual objective →∞.

5.5 Show that the linear program

Minimize x

+ x

= z

subject to 2x

+3x

≥ 3

− 2x

≥ 4

≤ 1

≥ 0,x

≥ 0

is infeasible. Write down its dual and show that a class of solutions exists for

which the dual objective →∞.

140 DUALITY

5.6 Consider the linear program:

Minimize −x

+ x

= z

subject to 2x

+3x

≥ 4

− x

≥ 1

≥ 0,x

≥ 0.

(a) Plot the feasible region of the primal and show that it is possible to construct

a class of solutions for which the primal objective z →−∞.

(b) Plot the feasible region of its dual and show that it is empty.

5.7 Use the DTZG Simplex Primal software option to show that the linear program

Minimize x

− 2x

+ x

= z

subject to x

− x

≥ 4

+ x

≥ 1

≥ 0,x

≥ 0

has a class of solutions for which the objective z →−∞. Write down the dual

and show that it is infeasible.

5.8 Consider the linear program

Minimize x

+2x

− 3x

= z

subject to 2x

+2x

+ x

≥ 10

− x

≤ 5

≥ 0,x

≥ 0.

(a) Use the DTZG Simplex Primal software option to solve the problem.

(b) Find its dual and use the DTZG Simplex Primal software option to solve it.

Theorem.

(d) Verify that complementary slackness holds at the primal and dual optima.

5.9 Consider the linear program

Minimize 2x

+ x

= z

subject to 2x

+ x

≤ 6

+3x

≥ 3

≥ 0,x

≥ 0.

(a) Plot the feasible region and solve the problem graphically.

(b) Find its dual and solve it graphically.

Weak Duality Theorem.

(d) Verify that complementary slackness holds at the primal and dual optima.

5.6 PROBLEMS 141

5.10 Dantzig [1963]. Show that neither the primal nor the dual of the system

Minimize x

− 2x

= z

subject to x

− x

≥ 2

−x

+ x

≥−1

≥ 0,x

≥ 0

has a feasible solution.

5.11 Write down the dual of the linear program

Minimize x

− 3x

+ x

= z

subject to 2x

− 3x

+ x

≥ 4

− x

≤ 2

− x

+ x

≤ 1

≥ 0,x

≥ 0.

Use the DTZG Simplex Primal software option to demonstrate that neither the

primal nor its dual has a feasible solution.

5.12 Prove that the optimal dual solution is never unique if the optimal primal basic

solution is degenerate and the optimal dual solution is not.

5.13 Prove in general that an equation in the primal corresponds to an unrestricted

variable in the dual and a variable unrestricted in sign corresponds to an equa-

tion.

5.14 Show that the dual of the linear program

Minimize b

y = z

subject to A

y =0,

y =1,

y ≥ 0,

where e =(1, 1,...,1)

, can be used to ﬁnd a feasible solution to Ax ≤ b. Note

that the x variables are not restricted in sign.

5.15 Consider an LP in standard form (3.1). Let B be the index set corresponding to

the basic variables (i.e., A

•B

is the submatrix consisting of the basic columns).

In terms of the original data, c, A, b, and B,

(a) What is π (the simplex multipliers)? Describe the pivot selection rules.

(b) Show that if x is optimal then π is dual feasible. (By x optimal, we mean

that x prices out optimally in our tableau.)

for the dual.

(d) Assume that our current tableau indicates that the problem is unbounded.

Show that there exists some vector 0 =¯x ≥ 0 such that A ¯x = 0 and c

¯x<0.

5.16 Let A be a skew symmetric matrix (that is, A

= −A). Show that the following

linear program is its own dual.

Minimize c

subject to Ax ≥−c

x ≥ 0.

If x

∗

is an optimal solution to the above linear program, what is the value of

∗

?Why?