Davidson K.R., Donsig A.P. Real Analysis with Real Applications
Подождите немного. Документ загружается.


15.8 The Franklin Wavelet 543
15.8.1. DEFINITION. A subset {x
n
: n ∈ Z} of a Hilbert space H is a Riesz
basis if span{x
n
: n ∈ Z} = H and there are constants A > 0 and B < ∞ so that
A
³
X
n
|a
n
|
2
´
1/2
≤
°
°
°
X
n
a
n
x
n
°
°
°
≤ B
³
X
n
|a
n
|
2
´
1/2
for all sequences (a
n
) with only finitely many nonzero terms.
15.8.2. THEOREM. The translates {h(x −j) : j ∈ Z} of the hat function form
a Riesz basis for V
0
.
PROOF. Consider the inner product of two compactly supported functions in V
0
,
say f (x) =
n
P
j=−n
a
j
h(x − j) and g(x) =
n
P
j=−n
b
j
h(x − j). For convenience, set
a
j
= b
j
= 0 for |j| > n.
hf, gi =
Z
+∞
−∞
f(x)g(x) dx =
n
X
j=−n−1
Z
j+1
j
f(x)g(x) dx
=
n
X
j=−n−1
Z
1
0
¡
a
j
+ (a
j+1
− a
j
)x
¢¡
b
j
+ (b
j+1
− b
j
)x
¢
dx
=
n
X
j=−n−1
a
j
b
j
+
1
2
a
j
(b
j+1
−b
j
)+
1
2
(a
j+1
−a
j
)b
j
+
1
3
(a
j+1
−a
j
)(b
j+1
−b
j
)
=
1
6
n
X
j=−n−1
2a
j
b
j
+ a
j
b
j+1
+ a
j
b
j+1
+ 2a
j+1
b
j+1
It is convenient to rearrange this sum further by moving the term 2a
j+1
b
j+1
to the
next index to obtain
hf, gi =
1
6
n
X
j=−n−1
4a
j
b
j
+ a
j
b
j+1
+ a
j
b
j+1
.
To make sense of this, we introduce two linear transformations.
Recall that `
2
(Z) is the Hilbert space of all square summable doubly indexed
sequences a = (a
n
)
+∞
−∞
, where we have
ha, bi =
(a
n
), (b
n
)
®
=
+∞
X
n=−∞
a
n
b
n
and kak
2
= ha, ai
1/2
=
³
+∞
X
n=−∞
a
2
n
´
1/2
.
Let e
k
for k ∈ Z denote the standard basis for `
2
(Z). Define the bilateral shift
on `
2
(Z) by Ue
k
= e
k+1
or (Ua)
n
= a
n−1
. It is easy to see that kUak
2
= kak
2
for all vectors a ∈ `
2
(Z). Also, it is clear that U maps `
2
(Z) one-to-one and onto
itself. Thus, U is a unitary map.
We also recall from linear algebra that the adjoint (or transpose since we are
working over the real numbers) of a linear transformation T is the linear map T
∗

544 Wavelets
such that
hT
∗
x, yi = hx, T yi for all vectors x, y ∈ H.
For the unitary operator U, we have that U
∗
= U
−1
is the backward bilateral shift
U
∗
e
k
= e
k−1
or (U
∗
a)
n
= a
n+1
.
Second, we define a linear map H from `
2
(Z) onto V
0
by
Ha =
+∞
X
n=−∞
a
n
h(x − n).
Looking back at our formula for the inner product in V
0
, we see that
hHa, Hbi =
1
6
n
X
j=−n−1
4a
j
b
j
+a
j
b
j+1
+a
j
b
j+1
=
1
6
(4I +U +U
∗
)a, b
®
.(15.8.3)
By the Cauchy–Schwarz inequality (7.3.4), since kUak
2
= kak
2
= kU
∗
ak
2
,
¯
¯
hUa, ai
¯
¯
=
¯
¯
hU
∗
a, ai
¯
¯
≤ kak
2
2
.
Hence we obtain
kfk
2
2
= hHa, Hai =
1
6
(4I + U + U
∗
)a, a
®
≤
1
6
¡
4kak
2
2
+ |hUa, ai| + |hU
∗
a, ai|
¢
≤ kak
2
2
.
Similarly, we obtain a lower bound
kfk
2
2
= hHa, Hai =
1
6
(4I + U + U
∗
)a, a
®
≥
1
6
¡
4kak
2
2
− |hUa, ai| − |hU
∗
a, ai|
¢
≥
1
3
kak
2
2
.
So while the translates of h are not an orthonormal set, we find that they do
form a Riesz basis for V
0
. ¥
Our problem now is to replace the hat function h by a scaling function ϕ. This
function ϕ must have the property that the translates ϕ(x −j) form an orthonormal
set spanning V
0
. We make use of another property relating the maps U and H. If
f(x) = Ha =
P
n
a
n
h(x − n), then
HUa =
X
n
a
n−1
h(x − n) =
X
n
a
n
h(x − n − 1)
= f (x − 1) = (T f)(x) = T Ha,
where T g(x) = g(x − 1) is the translation operator. So HU = T H, namely H
carries a translation by U in `
2
(Z) to translation by 1 in V
0
. This suggests that if
we can find a vector c such that the translates U
n
c form an orthonormal basis with
respect to the inner product
[a, b] =
1
6
(4I + U + U
∗
)a, b
®
,
then ϕ = Hc will be the desired scaling function. Indeed, (15.8.3) becomes
hHa, Hbi = [a, b].

15.8 The Franklin Wavelet 545
We make use of the correspondence between `
2
(Z) and L
2
(−π, π) provided
by complex Fourier series (see Remark 14.1.5). We identify the basis e
k
with
e
ikθ
, which is an orthonormal basis for L
2
(−π, π). This identifies the sequence
a in `
2
(Z) with the function in L
2
(−π, π) given by f(θ) =
+∞
P
n=−∞
a
n
e
inθ
. Now
compute
Uf(θ) = U
X
n
a
n
e
inθ
=
X
n
a
n
e
i(n+1)θ
= e
iθ
f(θ).
Thus U is the operator that multiplies f(θ) by e
iθ
. We will write M
g
to denote the
operator on L
2
(−π, π) that multiplies by g. Such operators are called multiplica-
tion operators. For example, U = M
e
iθ
. Hence
1
6
(4I + U + U
∗
) =
1
6
(4I + M
e
iθ
+ M
∗
e
iθ
)
= M
1
6
(4+e
iθ
+e
−iθ
)
= M
1
3
(2+cosθ)
.
15.8.4. THEOREM. There is an `
2
sequence (c
j
) so that ϕ(x) =
P
j
c
j
h(x−j)
is a scaling function for V
0
.
PROOF. Define the operator X = M
g
, where g(θ) =
√
3(2 + cos θ)
−1/2
. Notice
that X = X
∗
, XU = U X and X
2
= 3M
−1
2+cosθ
= 6(4I + U + U
∗
)
−1
. Now define
c = Xe
0
and ϕ = Hc. Compute
ϕ(x − j), ϕ(x − k)
®
= hT
j
Hc, T
k
Hci = hHU
j
c, HU
k
ci
= [U
j
c, U
k
c] =
1
6
(4I + U + U
∗
)U
j
c, U
k
c
®
= hX
−2
U
j
Xe
0
, U
k
Xe
0
i = hX
−2
XU
j
e
0
, XU
k
e
0
i
= hXX
−2
XU
j
e
0
, U
k
e
0
i = hU
j
e
0
, U
k
e
0
i = δ
jk
.
This shows that the translates of ϕ form an orthonormal set in the subspace V
0
.
Since e
0
is identified with the constant function 1,
ϕ(x) = HX1 = Hg.
To compute Hg, we need to find the (complex) Fourier series g ∼
P
n
c
n
e
inθ
. Now
g is an even function and thus c
−n
= c
n
; and so g ∼ c
0
+
∞
P
n=1
2c
n
cosnθ. Moreover,
c
n
= c
−n
=
√
3
2π
Z
π
−π
cosnθ
√
2 + cos θ
dθ for n ≥ 0.
Hence
(15.8.5) ϕ(x) =
+∞
X
n=−∞
c
n
h(x − n).
This is the continuous piecewise linear function with nodes at the integers taking
the values ϕ(n) = c
n
.

546 Wavelets
A similar argument shows that the translates of ϕ span all of V
0
. Indeed, note
that
He
ijθ
g = HU
j
g = T
j
Hg = ϕ(x − j).
Now h = He
0
= HXg
−1
. Express g
−1
(x) =
p
(2 + cos θ)/3, which is continu-
ous, as a complex Fourier series g
−1
∼
P
j
b
j
e
ijθ
. Then
(15.8.6) h = HXg
−1
= H
X
j
b
j
e
ijθ
g =
X
j
b
j
ϕ(x − j).
This expresses h as an `
2
combination of the orthonormal basis of translates of ϕ,
and thus h lies in their span. Evidently, this span also contains all translates of h,
and so they span all of V
0
. Therefore, ϕ is the desired scaling function. ¥
Using two formulas from the previous proof, we can write the scaling relation
for ϕ, in terms of the sequences (b
n
) and (c
n
). Verify that the hat function satisfies
the simple scaling relation
h(x) =
1
2
h(2x − 1) + h(2x) +
1
2
h(2x + 1).
Equation (15.8.6) gives
h(2x) =
X
j
b
j
ϕ(2x − j)
and similar formulas for h(2x − 1) and h(2x + 1). Putting these formulas into the
scaling relations gives h(x) as an infinite series involving ϕ(2x − k) as k ranges
over the integers. Substituting this series for h in Equation (15.8.5), we obtain
ϕ(x) =
X
l∈Z
³
X
j∈Z
c
j
£
b
2j−l
+
1
2
b
2j−l+1
+
1
2
b
2j−l−1
¤
´
ϕ(2x − l).
This formula does not appear tractable, but the sequences (c
n
) and (b
n
) decay quite
rapidly, so it is possible to obtain reasonable numerical results by taking sums over
relatively small ranges of j, say −10 to 10.
We can then apply Theorem 15.4.2 to obtain a formula for the Franklin wavelet
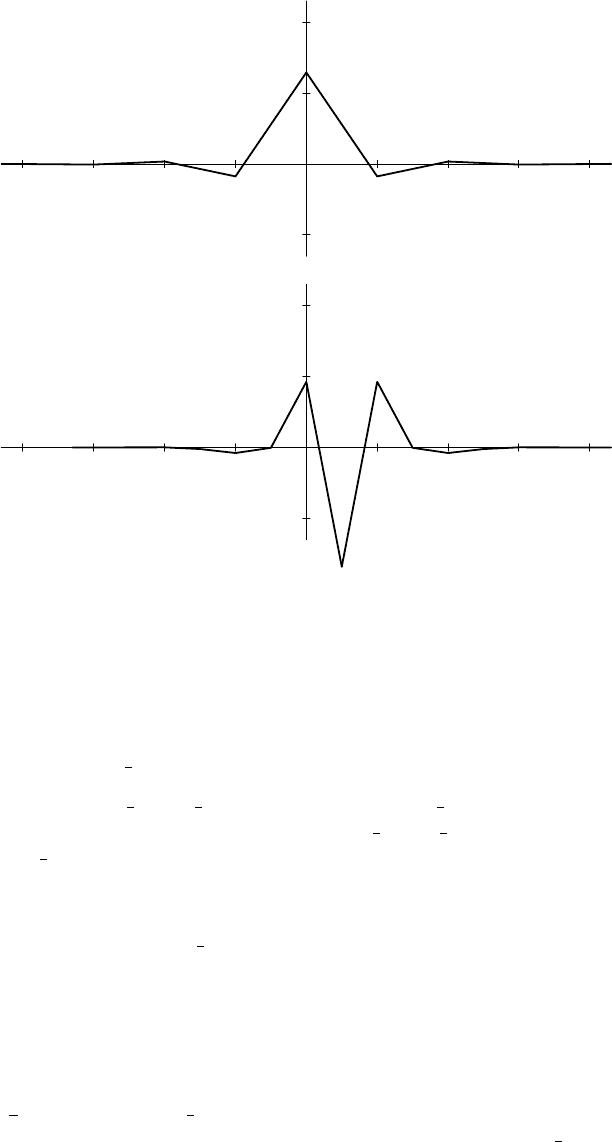
itself. This is plotted in Figure 15.6, along with the scaling relation. Notice that the
wavelet is continuous and piecewise linear with nodes at the half integers, as we
would expect since Theorem 15.4.2 implies that the wavelet is in V
1
. Incidentally,
the numerical values of the first few a
n
in the scaling relation for ϕ are
a
0
= 1.15633, a
1
= a
−1
= .56186, a
2
= a
−2
= −.09772,
a
3
= a
−3
= −.07346, a
4
= a
−4
= −.02400.
Exercises for Section 15.8
These exercises are all directed toward the analysis of a different wavelet, known as the
Str
¨
omberg wavelet, that has the same multiresolution subspaces V
k
as the Franklin
wavelet. See [36] for more details.
Write P L(X) to denote the space of L
2
(R) functions that are continuous and piece-
wise linear with nodes on a discrete subset X of R. Let h be the hat function.
15.8 The Franklin Wavelet 547
x
0
1−1 2−2 3−3 4−4
y
−1
1
2
ϕ
x
0
1−1 2−2 3−3 4−4
y
−1
1
2
ψ
FIGURE 15.6. The Franklin scaling function and wavelet.
A. Show that P L(−
1
2
N
0
∪ N) is spanned by {h(2x + k + 1), h(x − k) : k ≥ 0}.
B. Show that P L(−
1
2
N
0
∪ {
1
2
} ∪ N) is spanned by P L(−
1
2
N
0
∪ N) and h(2x). Hence
show that there is a norm 1 function ψ in P L(−
1
2
N
0
∪ {
1
2
} ∪ N) that is orthogonal to
P L(−
1
2
N
0
∪ N).
C. Show that ψ is orthogonal to 2
−k/2
ψ(2
−k
x − j) for all k < 0 and j ∈ Z and to
ψ(x + j) for j > 0. Hence deduce that {ψ
kj
: k, j ∈ Z} is orthonormal.
HINT: Some are in P L(−
1
2
N
0
∪ N). Do a change of variables for the rest.
D. Let V
k
= P L(2
−k
Z) and let W
k
be the orthogonal complement of V
k
in V
k+1
. Show
that span{ψ
kj
: j ∈ Z} = W
k
. Hence deduce that ψ is a wavelet.
HINT: Show that the span{ψ
0j
: −n ≤ j ≤ n} is the orthogonal complement of
P L(Z∪{k/2 : k ≤ −2n −1}) in PL(Z ∪{k/2 : k ≤ 2n +1}). Let n tend to infinity.
E. The piecewise linear continuous function ψ is determined by its values at the nodes,
ψ(
k
2
) = a
k
for k ≤ 0, ψ(
1
2
) = b and ψ(k) = c
k
for k ≥ 1. Show that the orthogonality
relations coming from the fact that ψ is orthogonal to the basis of PL(−
1
2
N
0
∪N) yield
548 Wavelets
the equations
a
k−1
+ a
k
+ a
k+1
= 0 for k≤ −1
c
k−1
+ c
k
+ c
k+1
= 0 for k ≥ 2
a
−2
+ 6a
−1
+ 10a
0
+ 6b + c
1
= 0
a
0
+ 6b + 13c
1
+ 4c
2
= 0.
Verify that the solution is the one-parameter family
a
k
= C(2
√
3 − 2)(
√
3 − 2)
|k|
for k ≤ 0
b = −C(
√
3 +
1
2
)
c
k
= C(
√
3 − 2)
k−1
for k ≥ 1.
F. Show that the Franklin scaling function is even, and deduce that the wavelet is sym-
metric about the line x =
1
2
. Show that the Str
¨
omberg wavelet does not have this
symmetry, and thus they are different wavelets with the same resolution.
15.9. Riesz Multiresolution Analysis
In this section, we will formalize the structure used in the previous section.
We then apply this to construct another family of wavelets, called Battle–Lemari
´
e
wavelets. Since they will be based on cubic splines, instead of the hat function,
they will be smoother than the Franklin wavelet. The following important charac-
terization of Riesz bases is our starting point.
15.9.1. THEOREM. A set of vectors {x
n
: n ∈ Z} in a Hilbert space H is a
Riesz basis if and only if there is a continuous linear map T from `
2
(Z) onto H
such that Te
n
= x
n
for n ∈ Z and there are constants 0 < A < B < ∞ such that
Akak
2
≤ kT ak ≤ Bkak
2
for all a ∈ `
2
(Z).
PROOF. Let `
0
denote the vector space of all sequences (a
n
) with only finitely
many nonzero terms. For any set {x
n
: n ∈ Z}, we may define a linear map from
`
0
into H by T a =
P
n
a
n
x
n
, which makes sense because the sum is finite.
Suppose that {x
n
: n ∈ Z} is a Riesz basis. The Riesz condition is readily
restated as
Akak
2
≤ kT ak ≤ Bkak
2
for all a ∈ `
0
.
In particular, the map T satisfies the Lipschitz condition
kT a − T bk = kT (a − b)k ≤ Bka − bk
2
and thus T is uniformly continuous.
Suppose that a ∈ `
2
(Z). Then we may choose a sequence a
n
in `
0
that con-
verges to a in the `
2
norm. Consequently, (a
n
) is a Cauchy sequence in `
2
(Z).
Therefore, since kT a
n
−T a
m
k ≤ Bka
n
−a
m
k
2
, it follows that (T a
n
) is a Cauchy
sequence in H. Since H is complete, we may define T a = lim
n
T a
n
. See the
Exercises for the argument explaining why this definition does not depend on the

15.9 Riesz Multiresolution Analysis 549
choice of the sequence. So the definition of T has been extended to all of `
2
(Z).
Moreover, we obtain that
kT ak = lim
n→∞
kT a
n
k ≤ B lim
n→∞
ka
n
k
2
= Bkak
2
.
So T is (uniformly) continuous on all of `
2
(Z).
We similarly obtain
kT ak = lim
n→∞
kT a
n
k ≥ A lim
n→∞
ka
n
k
2
= Akak
2
.
Clearly T maps `
0
onto the set of all finite linear combinations of {x
n
: n ∈ Z}.
So the range of T is dense in H by hypothesis.
Let y ∈ H. Choose vectors y
n
∈ span{x
n
: n ∈ Z} that converge to y. Then
(y
n
) is a Cauchy sequence. Since y
n
belongs to the range of T , there are vectors
a
n
∈ `
0
with T a
n
= y
n
. Therefore,
ka
n
− a
m
k
2
≤ A
−1
kT (a
n
− a
m
)k = A
−1
ky
n
− y
m
k.
Consequently, (a
n
) is Cauchy. Since `
2
(Z) is complete by Theorem 7.5.8, we
obtain a vector a = lim
n
a
n
. The continuity of T now ensures that
T a = lim
n→∞
T a
n
= lim
n→∞
y
n
= y.
So T maps `
2
(Z) onto H.
Conversely, if the operator T exists, then the Riesz norm condition holds (by
restricting T to `
0
). Now because T is continuous and `
0
is dense in `
2
(Z), it
follows that span{x
n
: n ∈ Z} = T `
0
is dense in T `
2
(Z) = H. That is,
span{x
n
: n ∈ Z} = H. ¥
15.9.2. COROLLARY. If {x
n
: n ∈ Z} is a Riesz basis for a Hilbert space H,
then every vector y ∈ H may be expressed in a unique way as y =
P
n
a
n
x
n
for
some a = (a
n
) in `
2
(Z).
PROOF. The existence of a vector a ∈ `
2
(Z) such that T a = y follows from
Theorem 15.9.1. Suppose that T b = y as well. Then T (a − b) = 0. However,
0 = kT (a −b)k ≥ Aka−bk
2
. Hence b = a. So T is one-to-one and a is uniquely
determined. ¥
15.9.3. REMARK. Note that the norm estimates show that the linear map T
has a continuous inverse. Indeed, Corollary 15.9.2 shows that T
−1
y = a is
well defined. It is easy to show that the inverse of a linear map is linear. Now
Theorem 15.9.1 shows that Akak
2
≤ kT ak. Substituting y = T a, we obtain
kT
−1
yk
2
≤
1
A
kyk for all y ∈ H. This shows that T
−1
is Lipschitz and hence
uniformly continuous.
In fact, a linear map is continuous if and only if it is bounded, meaning that
kT k = sup{kT xk : kxk = 1} is finite. (See Exercise 15.9.D.) A basic theorem
of functional analysis known as Banach’s Isomorphism Theorem states that a

550 Wavelets
continuous linear map between complete normed spaces that is one-to-one and onto
is invertible. Consequently, the existence of the constants A and B required in
Theorem 15.9.1 are automatic if we can verify that T is a bijection.
Now we specialize these ideas to a subspace V
0
of L
2
(R) spanned by the trans-
lates of a single function h. To obtain a nice condition, we need to know some easy
facts about multiplication operators. Let g ∈ C[−π, π]. Recall that the linear map
M
g
on L
2
(−π, π) is given by M
g
f(θ) = g(θ)f(θ).
15.9.4. PROPOSITION. Suppose that the complex Fourier series of g is given
by g ∼
P
k
t
k
e
ikθ
. Then the matrix
£
a
ij
¤
of M
g
with respect to the orthonormal
basis {e
ikθ
: k ∈ Z} for L
2
(−π, π) is given by a
jk
= t
j−k
.
PROOF. This is an easy computation. Indeed,
a
jk
= hM
g
e
ikθ
, e
ijθ
i =
1
2π
Z
π
−π
g(θ)e
ikθ
e
ijθ
dθ
=
1
2π
Z
π
−π
g(θ)
e
i(j−k)θ
dθ = t
j−k
.
¥
We also need these norm estimates for M
g
.
15.9.5. THEOREM. If g ∈ C[−π, π], then M
g
is a continuous linear map
on L
2
(−π, π) such that kM
g
fk
2
≤ kgk
∞
kfk
2
. Moreover, kgk
∞
is the smallest
constant B such that kM
g
fk
2
≤ Bkf k
2
for all f.
Similarly, if A = inf{|g(θ)| : θ ∈ [−π, π]}, then A is the largest constant such
that kM
g
fk
2
≥ Akfk
2
for all f ∈ L
2
(−π, π).
PROOF. A straightforward calculation shows that
kM
g
fk
2
2
=
1
2π
Z
π
−π
|g(θ)|
2
|f(θ)|
2
dθ ≤
1
2π
Z
π
−π
kgk
2
∞
|f(θ)|
2
dθ
= kgk
2
∞
1
2π
Z
π
−π
|f(θ)|
2
dθ = kgk
2
∞
kfk
2
2
.
In particular, M
g
is Lipschitz and hence continuous. Similarly,
kM
g
fk
2
2
=
1
2π
Z
π
−π
|g(θ)|
2
|f(θ)|
2
dθ ≥
1
2π
Z
π
−π
A
2
|f(θ)|
2
dθ = A
2
kfk
2
2
.
On the other hand, suppose that B < C < kgk
∞
. Then there is an nonempty
open interval (a, b) on which |g(θ)| > C. Let f be a continuous function on [−π, π]

15.9 Riesz Multiresolution Analysis 551
such that kfk
2
= 1 and the support of f is contained in [a, b]. Then
kM
g
fk
2
2
=
1
2π
Z
π
−π
|g(θ)|
2
|f(θ)|
2
dθ =
1
2π
Z
b
a
|g(θ)|
2
|f(θ)|
2
dθ
≥
1
2π
Z
b
a
C
2
|f(θ)|
2
dθ = C
2
1
2π
Z
π
−π
|f(θ)|
2
dθ > B
2
kfk
2
2
.
Therefore, Bkf k
2
is not an upper bound for kM
g
fk for all f . So kgk
∞
is the
optimal choice.
Likewise, if D > C > A, there is a continuous function f with kfk
2
= 1
supported on an interval (c, d) on which |g(θ)| < C. The same calculation shows
that kM
g
fk ≤ Ckfk
2
< Dkfk
2
. Therefore, A is the best constant in the lower
bound. ¥
We are now ready to obtain a practical characterization of when the translates
of h form a Riesz basis.
15.9.6. THEOREM. Let h ∈ L
2
(R) and V
0
=
span{h(x − j) : j ∈ Z}. Set
t
j
= hh(x), h(x −j)i for j ∈ Z. Assume that there is a continuous function g with
Fourier series t
0
+
P
∞
j=1
2t
j
cosjθ. Then {h(x − j) : j ∈ Z} is a Riesz basis for
V
0
if and only if there are constants 0 < A
2
≤ B
2
such that A
2
≤ g(θ) ≤ B
2
for
all −π ≤ θ ≤ π.
PROOF. Let T a =
P
n
a
n
h(x − n) for all a ∈ `
0
. By Theorem 15.9.1, the set
{h(x − j) : j ∈ Z} is a Riesz basis for V
0
if and only if there are constants
0 < A
2
≤ B
2
< ∞ such that
A
2
kak
2
2
≤ kT ak
2
=
°
°
°
X
n
a
n
h(x − n)
°
°
°
2
2
≤ B
2
kak
2
2
.
Now
kT ak
2
= hT a, T ai = hT
∗
T a, ai
The linear map T
∗
T has a matrix
£
t
ij
¤
with respect to the orthonormal basis e
n
given by
t
ij
= hT
∗
T e
j
, e
i
i = hT e
j
, T e
i
i
= hh(x − j), h(x − i)i = hh(x), h(x − i + j)i = t
i−j
.
So the matrix of T
∗
T is constant on diagonals. Note that by symmetry, t
−k
= t
k
.
All orthonormal bases are created equal, so we can identify e
n
with e
inθ
in
L
2
(−π, π), so that `
0
corresponds to all finite complex Fourier series. With this
identification, we see from Proposition 15.9.4 that T
∗
T = M
g
, where
g(θ) =
X
k
t
k
e
ikθ
= t
0
I +
∞
X
k=1
2t
k
coskθ.
We used t
−k
= t
k
to obtain a real function g, which returns us to the real domain
from this brief foray into complex vector spaces.

552 Wavelets
Next we observe that g(θ) ≥ 0. Indeed, we have
1
2π
Z
π
−π
g(θ)|f(θ)|
2
dθ = hT
∗
T f, fi = kT fk
2
2
≥ 0.
Suppose that g were not positive. Then by the continuity of g, we may choose an
interval (a, b) on which g(θ) < −ε < 0. Then as in the proof of Theorem 15.9.5,
we deduce that for any continuous function f supported on [a, b] we have
1
2π
Z
π
−π
g(θ)|f(θ)|
2
dθ ≤ −εkfk
2
2
< 0
which contradicts the previous inequality. So g is positive.
This allows us to define the multiplication operator M
√
g
. Since
√
g ≥ 0, we
find that M
∗
√
g
= M
√
g
.
T
∗
T = M
g
= M
2
√
g
= M
∗
√
g
M
√
g
(Be warned that this does not show that T is equal to M
√
g
. They do not even map
into the same Hilbert space.) Consequently,
kT fk
2
2
= hT
∗
T f, fi = hM
g
f, fi = hM
√
g
f, M
√
g
fi = kM
√
g
fk
2
2
.
Finally, an application of Theorem 15.9.5 shows that
A
2
kfk
2
2
≤ kM
√
g
fk
2
2
≤ k
√
gk
2
∞
kfk
2
2
= kgk
∞
kfk
2
2
for all f ∈ L
2
(−π, π) if and only if
A
2
≤ inf
θ∈[−π,π]
|
√
g(θ)|
2
= inf
θ∈[−π,π]
|g(θ)|.
Thus A
2
> 0 is possible only if g is bounded away from 0. ¥
We are now ready to modify a Riesz basis of translations of h to obtain an
orthonormal basis of translates. This is the keyto finding waveletsby the machinery
we have already developed.
15.9.7. THEOREM. Let h ∈ L
2
(R) be a function such that the set of translates
{h(x−j) : j ∈ Z}is a Riesz basis for its span V
0
. Assume that t
0
+
P
∞
j=1
2t
j
cosjθ
is the Fourier series of a continuous function, where t
k
= hh(x), h(x − k)i. Then
there is a function ϕ ∈ L
2
(R) such that {ϕ(x − j) : j ∈ Z} is an orthonormal
basis for V
0
.
PROOF. By Theorem 15.9.1, there is a continuous, invertible linear map T from
`
2
(Z) ontoV
0
given by T a =
P
n
a
n
h(x−n). By Theorem 15.9.6, the (continuous)
function g with Fourier series t
0
+
P
∞
j=1
2t
j
cosjθ satisfies T
∗
T = M
g
and there
are constants 0 < A
2
≤ B
2
< ∞ so that
A
2
≤ g(θ) ≤ B
2
for all − π ≤ θ ≤ π.
In particular, g
−1/2
is bounded above by 1/A.
