Davidson K.R., Donsig A.P. Real Analysis with Real Applications

Подождите немного. Документ загружается.

16.4 Extreme Points 573

G. (a) Suppose A ⊂ R

is convex and H = {x ∈ R

: hx, hi ≤ α} is a nontrivial

supporting hyperplane of A. If a ∈ A and ha, hi = α, show that a ∈ rbd(A).

(b) Show that an open convex set in R

is the intersection of all the open half-spaces

that contain it.

H. Suppose that S ⊂ R

and x ∈ conv(S) lies in the relative boundary rbdS. Prove that

there are n points s

, . . . , s

in S so that x ∈ conv{s

, . . . , s

HINT: Use a supporting hyperplane and Carath

eodory’s Theorem.

I. Farkas Lemma. Let A ⊂ R

and let C =

cone(A) be the closed convex cone

generated by A. Prove that exactly one of the following statements is valid: (1) x ∈ C

or (2) there is an s ∈ R

so that hx, si > 0 ≥ ha, si for all a ∈ A.

J. Let A = {a

, . . . , a

} be a ﬁnite subset of R

. Prove that the following are equivalent:

(1) 0 ∈ conv(A)

(2) There is no y ∈ R

so that ha, yi < 0 for all a ∈ A.

(3) f(x) = log

i=1

,xi

is bounded below on R

HINT: (1) ⇔ (2) separation. Not (2) ⇒ not (3), use f(ty). (2) ⇒ (3), easy.

K. Suppose that A, B, and C are closed convex sets in R

with A + C = B + C.

(a) Is it true that A = B?

(b) What if all three sets are compact?

L. (a) Prove that for any subset S of R

, a vector b belongs to

conv(S) if and only if

hb, xi ≤ sup{hs, xi : s ∈ S} for all x ∈ R

(b) Show that the intersection of all closed half-spaces containing S equals convS.

M. A hyperplane H properly separates A and B if A ⊂ H

−

, B ⊂ H

and A ∪B is not

contained in H. Prove that two convex sets A and B can be properly separated if and

only if ri(A) ∩ ri(B) = ∅.

HINT: Let C = A − B. Show 0 /∈ ri(C), and separate 0 from C.

16.4. Extreme Points

16.4.1. DEFINITION. Let A be a nonempty convex set. A point a ∈ A is an

extreme point of A if: Whenever a

, a

∈ A and a = (a

+ a

)/2, then a

= a

The set of all extreme points of A is denoted extA.

A face of A is a (convex) subset F of A such that whenever a

, a

∈ A and the

open interval (a

, a

) intersects F , then [a

, a

] is contained in F .

It is evident that a face is convex, and that a one point face is an extreme point.

Conversely, an extreme point is a one point face. For if (a

, a

) contains a, then a

is the average of two points of [a

, a

] with one of them being an endpoint. Thus

both those points equal a, and hence [a

, a

] = {a}.

Every convex set has two trivial faces, the whole set and the empty set. This

could be all of them, but often there is a rich collection.

16.4.2. EXAMPLES.

(1) Consider a cube in R

. The whole set and ∅ are faces for trivial reasons. The

extreme points are the eight vertices. Note that there are many other boundary

574 Convexity and Optimization

points that are not extreme. The one-dimensional faces are the twelve edges, and

the two-dimensional faces are the six sides (which are commonly called faces).

(2) On the other hand, consider the open unit ball U in R

. Except for the two

trivial cases, there are no extreme points or faces at all. For if F is a proper convex

subset, let a ∈ F and b ∈ U \F . Then since a is an interior point, the line segment

[b, a] may be extended to some point c ∈ U. Hence (b, c) ∩ F contains a but [b, c]

is not wholly contained in F .

(3) The closed unit ball B has many extreme points. A modiﬁcation of the previous

argument shows that no interior point is extreme. But every boundary point is

extreme. This follows from the proof of Lemma 16.4.3. There are no other faces

of the ball except for the two trivial cases.

16.4.3. LEMMA. Every compact convex set A has an extreme point.

PROOF. The norm function f(x) = kxk is continuous on A, and thus by the Ex-

treme Value Theorem (Theorem 5.4.4) f achieves its maximum value at some point

∈ A, say ka

k = R ≥ kak for all a ∈ A. Suppose that a

, a

∈ A and

= (a

+ a

)/2. Then by the Schwarz inequality (4.1.1),

= ka

+ a

+ 2ha

, a

i + ka

≤

+ 2ka

kka

k + ka

≤

+ 2R

+ R

) = R

Equality at the extremes forces the equalities ha

, a

i = ka

kka

k in the Schwarz

inequality and ka

k = ka

k = R. Hence a

= a

, and a

is extreme. ¥

We collect a couple of very easy lemmas that produce faces.

16.4.4. LEMMA. If F is a face of a convex set A, and G is a face of F , then G

is a face of A.

PROOF. Suppose that a

, a

∈ A such that (a

, a

) intersects G. Then a fortiori,

, a

) intersects F . As F is a face of A, it follows that [a

, a

] is contained in

F . Therefore, a

, a

∈ F and since G is a face of F , it follows that [a

, a

] is

contained in G. So G is a face of A. ¥

16.4.5. LEMMA. If A is a convex set in R

and H is a supporting hyperplane,

then H ∩A is a face of A.

PROOF. Let H = {x : hx, hi = α} be a hyperplane such that A is contained in

−

= {x : hx, hi ≤ α}. Let F = H ∩ A. Suppose that a

, a

∈ A such that

16.4 Extreme Points 575

, a

) ∩ F contains a point a = λa

+ (1 − λ)a

for λ ∈ (0, 1). Then

α = ha, hi = λha

, hi + (1 −λ)ha

, hi ≤ λα + (1 −λ)α = α.

Thus equality holds, so ha

, hi = ha

, hi = α. Therefore a

, a

belong to F . ¥

We have set the groundwork for a fundamental result that demonstrates the

primacy of extreme points.

16.4.6. MINKOWSKI’S THEOREM.

Let C be a nonempty compact convex subset of R

. Then C = conv(extC).

PROOF. We will prove this by induction on dimC. If dimC = 0, then C is a single

point, and it is evidently extreme. Suppose that we have established the result for

compact convex sets of dimension at most k − 1, and that dim C = k.

Let a be any point in rbd(C). By the Support Theorem (Theorem 16.3.7), there

is a nontrivial supporting hyperplane H to C at a. By Lemma 16.4.5, F = H ∩ C

is a face of C. Also, F is compact because C is compact and H is closed, and it is

nonempty since a ∈ F .

Note that aff(F) is contained in aff(C) ∩ H. This is properly contained in

aff(C) because C is not contained in H. Therefore, dim F < dim C = k. By

the induction hypothesis, F is the convex hull of its extreme points. However, by

Lemma 16.4.4, extF is contained in extC. So conv(extC) contains every bound-

ary point of C.

Finally, let a ∈ ri(C), and ﬁx another point b ∈ C. Let L be the line passing

through a and b. In particular, L is contained in aff(C). Then L ∩ C is a closed

bounded convex subset of L and thus is a closed interval that contains a in its

relative interior. Let a

, a

be the two endpoints. These points lie in rbd(C) because

any ball about a

meets L in points outside of C. By the previous paragraph, both

, a

lie in conv(extC). But a belongs to conv{a

, a

}and hence is also contained

in conv(extC). ¥

Exercises for Section 16.4

A. Let A ⊂ R

be convex. Show that no point in ri(A) is an extreme point.

B. Let A ⊂ R

be convex. Show that a ∈ A is an extreme point if and only if A\{a} is

convex.

C. Show that if B ⊂ A are two convex sets, then any extreme point of A that is contained

in B is an extreme point of B.

D. Find a nonempty proper closed convex subset of R

with no extreme points.

E. A face of a convex set A of the form A ∩ H, where H is a hyperplane, is called an

exposed face. Let A =

(0) ∪ {(x, y) : 0 ≤ x ≤ 1, |y| ≤ 1}. Show that (0, 1) is an

extreme point that is not exposed.

F. Let A ⊂ R

be compact and convex, and let f be an afﬁne map of R

into R.

(a) Show that {a ∈ A : f(a) = sup

x∈A

f(x)} is an exposed face of A.

576 Convexity and Optimization

(b) Let A be a compact convex set, and let B ⊂ R

such that A = conv(B). Prove

that B contains ext(A).

at an extreme point.

G. Let A = [0, 1]

= {x = (x

, . . . , x

) ∈ R

: 0 ≤ x

≤ 1, 1 ≤ i ≤ n}.

(a) Describe ext(A).

(b) Explicitly show that each a ∈ A is in the convex hull of n + 1 extreme points.

HINT: If x

≤ x

≤ ··· ≤ x

, consider e

, where e

= 1 if i > j and 0 otherwise,

0 ≤ j ≤ n.

H. A polyhedral set is the intersection of a ﬁnite number of closed half-spaces. Let A be

a closed bounded polyhedral set determined by the intersection of closed half-spaces

−

for 1 ≤ i ≤ p.

(a) Show that if a ∈ A is not in any hyperplane H

, then a belongs to ri(A).

(b) Show that every extreme point of A is the intersection of some collection of the

hyperplanes H

. HINT: Use part (a) and induction on dim A.

just before Lemma 16.2.4.

I. Let A = conv{a

, . . . , a

} be a polytope.

(a) Show that extA is contained in {a

, . . . , a

(b) Show that every face of A is the convex hull of a subset of {a

, . . . , a

HINT: Apply the Support Theorem to a point in ri(F ).

(d) Prove that the intersection of half-spaces determined by (c) is a polyhedral set P

containing A such that each face of A is contained in rbd(P ).

(e) Show that P = A.

HINT: If p ∈ P \ A and a ∈ ri(A), consider where [a, p) intersects rbd(A).

(f) Hence show that every polytope is a closed bounded polyhedral set.

16.5. Convex Functions in One Dimension

Convex functions occur frequently in many applications. Generally, we are in-

terested in minimizing these functions over a convex set determined by a number of

constraints, a problem that we will discuss in later sections. The notion of convex-

ity allows us to work with functions that need not be differentiable. The analysis

of convex functions can be thought of an an extension of calculus to an important

class of nondifferentiable functions.

While a few generalities are introduced here for functions on domains in R

most of this section is devoted to convex functions on the line. In the next section,

we extend these notions to higher dimensions.

16.5.1. DEFINITION. Suppose that A is a convex subset of R

. A real-valued

function f deﬁned on A is called a convex function if

λx + (1 −λ)y

≤ λf(x) + (1 − λ)f (y) for all x, y ∈ A, 0 ≤ λ ≤ 1.

A function f is called a concave function if −f is convex.

16.5 Convex Functions in One Dimension 577

16.5.2. EXAMPLES.

(1) All linear functions are both convex and concave.

(2) If ||| · ||| is any norm on R

, the function f(x) = |||x||| is convex. Indeed, the

triangle inequality and homogeneity yield

|||λx + (1 − λ)y||| ≤ λ|||x|||+ (1 − λ)|||y||| for x, y ∈ R

and 0 ≤ λ ≤ 1,

which is precisely the convexity condition.

(3) f (x) = e

is convex. This is evident from an inspection of its graph. We will

see that any C

function g with g

≥ 0 is convex. Since f

(x) = e

> 0, this

result applies.

This next result, an easy application of the Mean Value Theorem, provides

many examples of convex functions on the line. It also shows that our deﬁnition is

consistent with the notion introduced in calculus.

16.5.3. LEMMA. Suppose that f is a differentiable function on (a, b) and f

monotone increasing. Then f is convex. In particular, this holds if f is C

and

≥ 0.

PROOF. Suppose that a < x < y < b and 0 < λ < 1. Let z = λx + (1 − λ)y.

Then there are points c ∈ (a, z) and d ∈ (z, y) so that

f(z) − f (x)

z − x

= f

(d) =

f(y) − f(z)

y − z

Substituting z − x = (1 − λ)(y − x) and y − z = λ(y − x) yields

f(z) − f (x)

1 − λ

≤

f(y) − f(z)

Just multiply this out to obtain the statement of convexity.

If f is C

and f

≥ 0, then f

is an increasing function. ¥

A straightforward induction on r gives the following result from the deﬁnition

of convexity. The proof is left as an exercise.

16.5.4. JENSEN’S INEQUALITY.

Suppose that A ⊂ R

is convex and f is a convex function on A. If a

, . . . , a

are

points in A and λ

, . . . , λ

are nonnegative scalars that sum to 1, then

f(λ

+ ··· + λ

) ≤ λ

f(a

) + ··· + λ

f(a

16.5.5. EXAMPLE. In spite of the fact that Jensen’s inequality is almost trivial,

when it is applied we can obtain results that are not obvious. Consider the exponen-

tial function f(x) = e

. Let t

, . . . , t

be positive real numbers and let a

= log t

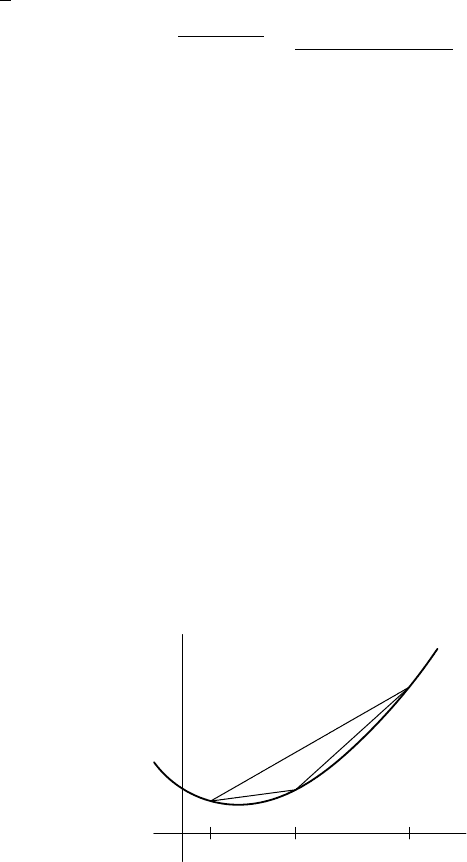
578 Convexity and Optimization

Then for positive values λ

with

i=1

= 1,

+···+λ

≤ λ

+ ··· + λ

In other words,

···t

≤ λ

+ λ

+ ··· + λ

This is the generalized arithmetic mean–geometric mean inequality. Setting

for 1 ≤ i ≤ n, we obtain

√

···t

≤

+ t

+ ··· + t

We begin by characterizing a convex function in terms of its graph, or rather its

epigraph. This also serves to justify the terminology.

16.5.6. DEFINITION. Let f be a real-valued function on a convex subset A of

. The epigraph of f is deﬁned to be epi(f) = {(a, y) ∈ A × R : y ≥ f (a)}.

16.5.7. LEMMA. Let f be a real-valued function on a convex subset A of R

Then f is a convex function if and only if epi(f) is a convex set.

PROOF. Suppose p = (x, t) and q = (y, u) belong to epi(f) and λ ∈ [0, 1]. Since

A is convex, z := λx+(1−λ)y ∈ A. Consider λp+(1−λ)q = (z, λt+(1−λ)u).

If f is convex, then

f(z) ≤ λf (x) + (1 −λ)f(y) ≤ λt + (1 −λ)u

and thus epi(f) is convex. Conversely, if epi(f) is convex, then using t = f(x)

and u = f(y) we see that epi(f ) contains (z, λf(x) + (1 − λ)f (y)) and hence

f(z) ≤ λf (x) + (1 −λ)f(y). That is, f is convex. ¥

Now we specialize to functions on the line. We begin with a lemma about

secants. In the next section, this will be applied to functions of more variables.

x y z

FIGURE 16.4. Secants of a convex function.

16.5 Convex Functions in One Dimension 579

16.5.8. SECANT LEMMA.

Let f be a convex function on [a, b], and consider three points a ≤ x < y < z ≤ b.

Then

f(y) − f(x)

y − x

≤

f(z) − f (x)

z − x

≤

f(z) − f (y)

z − y

PROOF. See Figure 16.4. Set λ =

z − y

z − x

, which lies in (0, 1). So y = λx+(1−λ)z.

By convexity, f(y) ≤ λf(x) + (1 − λ)f(z). Therefore,

f(y) − f(x) ≤ (1 − λ)

f(z) − f (x)

Divide by y − x = (1 −λ)(z − x) to obtain

f(y) − f(x)

y − x

≤

(1 − λ)

f(z) − f (x)

(1 − λ)(z − x)

as desired. The second inequality is similar. ¥

The main result about convex functions of one real variable is that convex func-

tions are almost differentiable in a certain strong sense. The absolute value function

on R shows that a convex function need not be differentiable, even at interior points

of its domain. However, it does have left and right derivatives everywhere.

Recall that a function f has a right derivative at a if lim

h→0

f(a + h) − f (a)

exists. It is denoted by D

f(a). Similarly, we deﬁne the left derivative to be the

limit D

−

f(a) := lim

h→0

f(a) − f(a − h)

when it exists.

16.5.9. THEOREM. Let f be a convex function deﬁned on (a, b). Then f has

left and right derivatives at every point, and if a < x < y < b, then

−

f(x) ≤ D

−

f(y) ≤ D

f(y).

Therefore, f is continuous.

PROOF. Let 0 < h < k be small enough that x±k belong to the interval (a, b).

Apply the Secant Lemma using x−k < x−h < x < x+h < x+k,

f(x) − f(x−k)

≤

f(x) − f(x−h)

≤

f(x+h) − f(x)

≤

f(x+k) − f(x)

Thus the quotient function d

(t) =

f(x+t) − f(x)

is an increasing function of t

on an interval [−k, k]. In particular, {d

(s) : s < 0} is bounded above by d

(t) for

any t > 0. Thus by the Least Upper Bound Principle (2.5.3),

−

f(x) = lim

s→0

f(x) − f(x−s)

= sup

s→0

f(x) − f(x−s)

580 Convexity and Optimization

exists. Similarly,

f(x) = lim

t→0

f(x+t) − f(x)

= inf

t→0

f(x+t) − f(x)

exists. Moreover, D

−

f(x) ≤ D

f(x) since d

(−s) ≤ d

(t) for all −s < 0 < t.

Another application of the lemma using x < x+t < y−s < y shows that

(t) =

f(x+t) − f(x)

≤

f(y) − f(y−s)

= d

(−s)

if s, t are sufﬁciently small and positive. Thus D

f(x) ≤ D

−

f(y).

In particular, since left and right derivatives exist, we have

lim

t→0

f(x + t) = lim

t→0

f(x) + t

f(x+t) − f(x)

= f (x) + 0D

f(x) = f(x).

Similarly, lim

s→0

f(x − s) = f(x). Therefore f is continuous. ¥

16.5.10. COROLLARY. Let f be a convex function deﬁned on (a, b). Then f is

differentiable except on a countable set of points.

PROOF. The right derivative D

f(x) is deﬁned at every point of (a, b) and is a

monotone increasing function. By Theorem 5.7.5, D

f is continuous except for a

countable set of jump discontinuities. At every point x where D

f is continuous,

we will show that D

−

f(x) = D

f(x). From the continuity of f, given any ε > 0,

there is an r > 0 so that |D

f(x±r) − D

f(x)| < ε. Now if 0 < h < r,

f(x − r) ≤ D

−

f(x − h) ≤ D

−

f(x)

≤ D

f(x) ≤ D

−

f(x + h) ≤ D

f(x + r).

Thus |D

−

f(x+h)−D

f(x)| < ε for all |h| < r. As ε > 0 is arbitrary, we deduce

that D

−

f(x) = D

f(x) and lim

h→0

−

f(x + h) = D

f(x). So D

−

f is continuous

at x and agrees with D

f(x). Consequently, f is differentiable at each point of

continuity of D

f. ¥

16.5.11. DEFINITION. Let f be a convex function on (a, b). For each x in

(a, b), the subdifferential of f at x is the set ∂f(x) = [D

−

f(x), D

f(x)].

See Figure 16.5. The geometric interpretation is the following pretty result.

When the convex function f is differentiable at c, this result says that epi(f) lies

above the tangent line to f through (c, f(c)), while any other line through this point

crosses above the graph.

16.5.12. PROPOSITION. Let f be a convex function on (a, b) and ﬁx a point

c ∈ (a, b). The line y = f(c) + m(x − c) is a supporting hyperplane of epi(f) at

(c, f(c)) if and only if m ∈ ∂f(c).

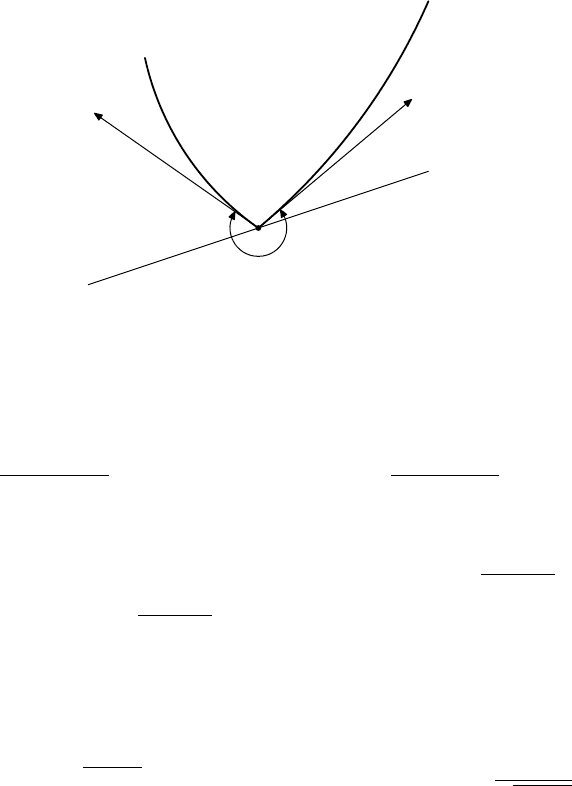
16.5 Convex Functions in One Dimension 581

−

f(x)

∂f (a)

FIGURE 16.5. The subdifferential and a tangent line at a non-

smooth point.

PROOF. Suppose that a < x < c < z < b and m ∈ ∂f(c). From the previous

proof,

f(c) − f(x)

c − x

≤ D

−

f(c) ≤ m ≤ D

f(c) ≤

f(z) − f (c)

z − c

Hence f(x) ≥ f(c) + m(x −c) and f(z) ≥ f(c) + m(z −c). So epi(f) lies above

the line, and thus y = f (c) + m(x − c) is a support line at (c, f(c)).

Conversely, suppose that m > D

f(c). Since D

f(c) = inf

z>c

f(z)−f (c)

z−c

, there

is some point z > x so that

f(z)−f (c)

z−c

< m. Thus f(z) < f (c) + m(z − c) and the

line intersects the interior of epi(f ), which is a contradiction. A similar argument

deals with m < D

−

f(c). ¥

16.5.13. EXAMPLE. There can be problems at the endpoints when f is de-

ﬁned on a closed interval, even if f is continuous there. For example, consider the

function f(x) = −

√

1 − x

on [−1, 1]. Then on (−1, 1), f

(x) =

√

1 − x

and

(x) = (1 − x

)

−3/2

. As f is C

and f

> 0 on (−1, 1), this function is convex.

It is differentiable at every interior point. However, at the two endpoints, the graph

has a vertical tangent. It is for this reason that we did not deﬁne the subdifferen-

tial at endpoints. If we wished to deﬁne them, the only reasonable deﬁnition for

∂f(±1) would be the empty set.

Exercises for Section 16.5

A. Show that if f and −f are convex, then f is afﬁne.

B. Show that the function f on [0, 1] given by f(x) = 0 for x < 1 and f(1) = 1 is a

discontinuous convex function. Why does this not contradict Theorem 16.5.9?

C. Prove Jensen’s inequality (Theorem 16.5.4).

582 Convexity and Optimization

D. Let f be a convex function on R and let g be any continuous function on [0, 1]. Show

that f

g(x) dx

≤

f(g(x)) dx.

HINT: Approximate the integrals by the Riemann sums.

E. (a) Apply the arithmetic mean–geometric mean inequality to t

= ··· = t

= 1 +

and t

n+1

= 1 and a second application with t

= ··· = t

n+1

and t

n+2

= 1.

(b) Hence prove that

1 +

≤

1 +

n+1

≤

1 +

n+1

n+2

≤

1 +

n+1

n→∞

1 +

exists.

HINT: Compare this approach with Proposition 3.3.1.

F. Suppose that A ⊂ R

is a convex set. Show that if f

, . . . , f

are convex functions on

A, then the function f(x) = max{f

(x) : 1 ≤ i ≤ k} is convex.

G. Suppose that {f

: i ∈ I} is a collection of convex functions such that for each x ∈ R,

g(x) = sup{f

(x) : i ∈ I} is ﬁnite. Show that g is convex.

H. Suppose that f is a convex function on R that is bounded above. Show that f is

constant.

I. (a) If f is a C

function on (a, b) such that f

(x) > 0 for all x ∈ (a, b), prove that

f is strictly convex: f(λx + (1 − λ)y) < λf(x) + (1 − λ)f(y) for x 6= y and

0 < λ < 1.

(b) Find an example of a strictly convex C

function on R such that f

(0) = 0.

J. Let f be a convex function on (a, b). Show that if f attains its minimum at c ∈ (a, b),

then 0 ∈ ∂f (c).

K. Convex Mean Value Theorem. Consider a continuous convex function f on [a, b].

Show that there is a point c ∈ (a, b) so that

f(b) − f(a)

b − a

∈ ∂f (c).

HINT: Adapt the proof of the Mean Value Theorem (Theorem 6.2.4). Consider the

function h(x) = f(x) − f(a) − [(f(b) − f(a))/(b − a)](x − a) and use the previous

exercise.

L. (a) If f is a convex function on (a, b) ⊃ [c, d], prove that f is Lipschitz on [c, d].

HINT: Theorem 16.5.9.

(b) Show by example that a continuous convex function on [a, b] need not be Lipschitz.

M. Suppose that a function f on (a, b) and satisﬁes f

x+y

≤

f(x) + f(y)

for all

x, y ∈ (a, b).

(a) Show by induction that f

+···+x

≤ 2

−k

f(x

)+···+f (x

)

for x

∈ (a, b).

(b) Prove that if f is continuous, then f is convex.

HINT: Take each x

to be either x or y.

N. Prove that f(x) = log

sinhax

sinhbx

is convex if 0 < b ≤ a as follows:

(a) Show that f

(x) > 0 for x 6= 0.

HINT: Show that g(x) = b sinhax − a sinh bx is increasing on [0, ∞).

(b) Find the second-order Taylor polynomial of f about 0 from your knowledge of

sinhx and log(1 + x). Deduce that f is twice differentiable at 0.