Davidson K.R., Donsig A.P. Real Analysis with Real Applications

Подождите немного. Документ загружается.

15.9 Riesz Multiresolution Analysis 553

Now compute the Fourier series of g

−1/2

, say

−1/2

∼

−inθ

= c

I +

∞

k=1

coskθ,

where

= c

−k

2π

−π

cosnθ

g(θ)

dθ.

We claim that the orthogonal generator is obtained by the formula

ϕ(x) = T g

−1/2

∞

n=−∞

h(x − n).

Indeed,



ϕ(x − j), ϕ(x − k)



T e

−ijθ

−1/2

(θ), T e

−ikθ

−1/2

(θ)



∗

T e

−ijθ

−1/2

(θ), e

−ikθ

−1/2

(θ)



−1/2

−ijθ

, M

−1/2

−ikθ



−1/2

−ijθ

, e

−ikθ



−ijθ

, e

−ikθ

= δ

So {ϕ(x − k) : k ∈ Z} is orthonormal.

It is clear that each ϕ(x − k) belongs to V

since they are in the span of the

h(x − j)’s. Conversely, observe that ϕ(x − k) = T M

−1/2

ikθ

. Thus

span{ϕ(x − k) : k ∈ Z} = T M

−1/2

(T) = T L

(T) = V

because M

is invertible and so M

−1/2

(T) = L

(T), and T maps L

(T) onto

by Corollary 15.9.2. So {ϕ(x − k) : k ∈ Z} is an orthonormal basis for V

. ¥

The second notion that arose in our construction of a continuous wavelet was a

weaker notion of a multiresolution using Riesz bases.

15.9.8. DEFINITION. A Riesz multiresolution of L

(R) with scaling function

h is the sequence of subspaces V

= span

h(2

x − j) : j ∈ Z

provided that the

sequence satisﬁes the following properties:

(1) Riesz basis: {h(x − j) : j ∈ Z} is a Riesz basis for V

(2) nesting: V

⊂ V

k+1

for all k ∈ Z.

(3) scaling: f(x) ∈ V

if and only if f(2x) ∈ V

k+1

(4) density:

k∈Z

= L

(R).

(5) separation:

k∈Z

= {0}.

The main result is now a matter of collecting our results.

554 Wavelets

15.9.9. THEOREM. Suppose that h is the scaling function for a Riesz multireso-

lution V

= span

h(2

x −j) : j ∈ Z

. Assume that there is a continuous function

with Fourier series khk

∞

j=1

2hh(x), h(n−k)icos jθ. Then there exists a scal-

ing function ϕ generating the same nested sequence of subspaces. Consequently,

there is a wavelet basis for L

(R) compatible with this decomposition.

PROOF. Theorem 15.9.7 provides an orthogonal scaling function for this resolu-

tion. Then Theorem 15.4.2 provides an algorithm for constructing the correspond-

ing wavelet. ¥

15.9.10. EXAMPLE. We ﬁnish this section by describing some smoother ex-

amples of wavelets, known as Battle–Lemari

e wavelets or B-spline wavelets. Let

[0,1)

. For each n ≥ 0, deﬁne

(x) = N

n−1

∗ N

(x) =

x−1

n−1

(t) dt.

For example, N

(x) = h(x − 1) is a translate of the hat function,

(x) =











for 0 ≤ x ≤ 1

− (x −

)

for 1 ≤ x ≤ 2

(3 − x)

for 2 ≤ x ≤ 3

and

(x) =











for 0 ≤ x ≤ 1

−

(x − 1)

for 1 ≤ x ≤ 2

(4 − x)

−

(3 − x)

for 2 ≤ x ≤ 3

(4 − x)

for 3 ≤ x ≤ 4.

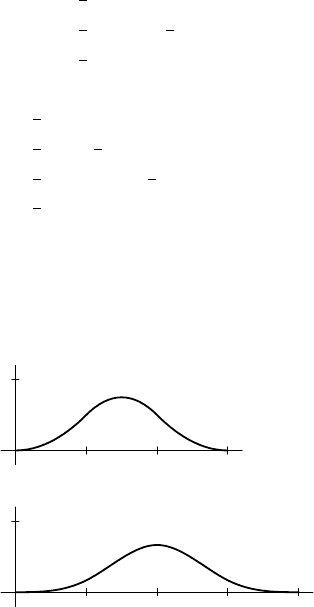
Figure 15.7 gives thegraphs of N

and N

. Notice that N

(x) isa cubic spline. That

is, N

is C

, has compact support, and on each interval [k, k+1] it is represented by

a cubic polynomial. See the Exercises for hints on establishing similar properties

for general n.

1 2 3

y = N

(x)

1 2 3 4

y = N

(x)

FIGURE 15.7. The graphs of N

and N

15.9 Riesz Multiresolution Analysis 555

Let S

(n)

denote the subspace of L

(R) consisting of splines of order n with

nodes at the points 2

−k

Z. These are the L

functions that have n − 1 continuous

derivatives such that the restriction to each dyadic interval [2

−k

j, 2

−k

(j + 1)] is a

polynomial of degree n. Clearly for each ﬁxed n, the sequence

··· ⊂ S

(n)

−2

⊂ S

(n)

−1

⊂ S

(n)

⊂ S

(n)

⊂ S

(n)

⊂ . . .

is nested and satisﬁes the scaling property.

In fact, for each n, this forms a Riesz multiresolution of L

(R) with scaling

function N

(x). We will establish this for n = 3.

Theorem 10.9.1 showed that every continuous function f on the closed interval

[−2

, 2

] is the uniform limit of a sequence of cubic splines h

with nodes at

−k

Z. These cubic splines may be chosen to have support in [−2

, 2

] as well.

Thus

lim

k→∞

kf − h

= lim

k→∞

−2

|f(x) − h

(x)|

dx ≤ 2

N+1

lim

k→∞

kf − h

∞

= 0.

So f is the limit in L

of a sequence of cubic splines. It follows that

(3)

dense in L

(R).

The separation property is established in much the same way as the piecewise

linear case. Suppose that f is a function in

(3)

. For k ≤ 0, functions in S

(3)

are cubic polynomials on [0, 2

|k|

] and on [−2

|k|

, 0]. Hence the restrictions of f to

[0, ∞) and to (−∞, 0] agree with cubic polynomials. A nonzero cubic polynomial

p has

∞

|p(x)|

dx = +∞ =

−∞

|p(x)|

dx.

So the only L

(R) function that is cubic on both half lines is the zero function.

Thus f = 0 is the only point in the intersection.

Finally, we will show that translates of N

(x) form a Riesz basis for L

(R).

By Theorem 15.9.6, we must compute t

= hN

(x), N

(x − j)i. By symmetry,

−k

= t

and the fact that N

is supported on [0, 4] means that t

= 0 for |k| ≥ 4.

Therefore, it sufﬁces to compute t

, t

, and t

. We spare the reader the tedious

calculation and use Maple to obtain

151

315

= t

−1

397

1680

= t

−2

= t

−3

5040

Thus we are led to consider the function

g(θ) =

1208

2520

1191

2520

cosθ +

2520

cos2θ +

2520

cos3θ.

An easy calculation shows that this takes its minimum when cosθ = −1 and the

minimum value is

2520

> 0. Since this function is positive, Theorem 15.9.9 shows

that there is a wavelet basis consisting of cubic splines.

556 Wavelets

Exercises for Section 15.9

A. Let ϕ =

[0,2)

. Show that {ϕ(x − j) : j ∈ Z} is not a Riesz basis for its span.

B. Show that if {h(x −j) : j ∈ Z} is a Riesz basis for V

, then {2

k/2

h(2

x −j) : j ∈ Z}

forms a Riesz basis for V

for each k ∈ Z.

C. Show that if T is an invertible linear map, then T

−1

is linear.

D. Let T be a linear map from one Hilbert space H to itself. Prove that T is continuous if

and only if it is bounded.

HINT: If not bounded, ﬁnd x

with kx

k → 0 while kT x

k → ∞.

E. Recall that `

is the nonclosed subspace of `

(Z) of elements with only ﬁnitely many

nonzero entries. Show that if T is a linear map from `

into a Hilbert space H with

kT ak ≤ Bkak

, then T extends uniquely to a continuous function on `

(Z) into H.

HINT: Fix a ∈ `

(Z) and ε > 0. Show that if b, c ∈ `

and both lie in the ε/(2B) ball

about a, then kT b − T ck < ε. Hence deduce that if (b

) and (c

) are two sequences

in `

converging to a, then lim

T b

= lim

T c

. Consequently, show that setting T a

to be this limit determines a continuous function on `

(Z) extending T .

F. Suppose that {x

: n ∈ Z} is a Riesz basis for H.

(a) Show that there is a unique vector y

orthogonal to the subspace

= span{x

: j 6= n} such that hx

, y

i = 1.

(b) Show that if z ∈ H, then z =

hz, y

: n ∈ Z} is a Riesz basis for H.

HINT: If (a

) ∈ `

, there is another sequence (b

) so that

Apply the Cauchy–Schwarz inequality to both



and



G. Show that {N

(x − k) : k ∈ Z} is a Riesz basis for its span.

H. Prove by induction on n ≥ 1 that

(a) N

is C

(n−1)

(b) N

[j,j+1]

is a polynomial of degree n for each j ∈ Z.

(x) > 0} = (0, n + 1).

(d)

(x − k) = 1 for all x ∈ R.

CHAPTER 16

Convexity and Optimization

Optimization is a central theme of applied mathematics that involves minimizing

or maximizing various quantities. This is an important application of the derivative

tests in calculus. In addition to the ﬁrst and second derivative tests of one-variable

calculus, there is the powerful technique of Lagrange multipliers in several vari-

ables. This chapter is concerned with analogues of these tests that are applicable

to functions that are not differentiable. Of course, some different hypothesis must

replace differentiability and this is the notion of convexity. It turns out that many

applications in economics, business, and related areas involve convex functions.

As in other chapters of this book, we concentrate on the theoretical underpinnings

of the subject. The important aspect of constructing algorithms to carry out our

program is not addressed. However, the reader will be well placed to read that

material. Results from both linear algebra and calculus appear regularly.

The study of convex sets and convex functions is a comparatively recent devel-

opment. Although convexity appears implicitly much earlier (going back to work

of Archimedes, in fact), the ﬁrst papers on convex sets appeared at the end of the

nineteenth century. The main theorems of this chapter, characterizations of solu-

tions of optimization problems, ﬁrst appeared around the middle of the twentieth

century. Starting in the 1970s, there has been considerable work on extending these

methods to nonconvex functions.

16.1. Convex Sets

Although convex subsets can be deﬁned for any normed vector space, we con-

centrate on R

with the Euclidean norm. For this space, we have an inner product

and the Heine–Borel Theorem (Theorem 4.4.6) characterizing compact sets in R

as useful tools.

16.1.1. DEFINITION. A subset A of R

is called a convex set if

λa + (1 −λ)b ∈ A for all a, b ∈ A and λ ∈ [0, 1].

557

558 Convexity and Optimization

Let [a, b] = {λa + (1−λ)b : λ ∈ [0, 1]} denote the line segment joining points

a and b in R

. Deﬁne (a, b), [a, b) and (a, b] in the analogous way. You should

note that λ ∈ (0, 1] corresponds to [a, b). Notice that A is convex if and only if

[a, b] ⊂ A whenever a, b ∈ A. See Figure 16.1

FIGURE 16.1. A convex and a nonconvex set.

16.1.2. DEFINITION. A subset A of R

is an afﬁne set if

λa + (1 −λ)b ∈ A for all a, b ∈ A and λ ∈ R.

A subset C of R

is a cone if it is a convex set that contains all of its positive scalar

multiples, that is,

λa ∈ C for all a ∈ C and λ > 0.

Clearly, afﬁne sets and cones are convex but not conversely.

Now is a good time to mention a related bit of terminology. In this chapter, we

reserve linear function for functions satisfying f(λa + µb) = λf(a) + µf(b), for

all a, b in the domain and all scalars λ and µ. We use afﬁne function for a function

g given by g(x) = f (x) + c, where f is a linear function and c is a constant. We

leave it as an exercise, Exericse 16.1.I, to show that a function f : R

→ R

linear or afﬁne if and only if the graph of f is either a subspace or an afﬁne set,

respectively.

Convex sets are ubiquitous and we give a few examples, mostly without proof.

Proving the following assertions is a useful warm-up exercise.

16.1.3. EXAMPLES.

(1) A subspace of R

is both afﬁne and a cone.

(2) Any ball B

(a) = {x ∈ R

: kx − ak ≤ r} in R

is convex. Indeed, if

x, y ∈ B

(a) and λ ∈ [0, 1], then

kλx + (1 −λ)y − ak = kλ(x − a) + (1 −λ)(y − a)k

≤ λkx − ak + (1 −λ)ky − ak

≤ λr + (1 −λ)r = r.

So λx + (1 −λ)y ∈ B

(a). Clearly, the ball is neither afﬁne nor a cone.

(3) The half-space {(x, y) : ax + by ≥ 0} is a closed convex cone in R

16.1 Convex Sets 559

(4) In R

, the positive orthant R

= {(x

, . . . , x

) : x

> 0} is a cone.

(5) If A ⊂ R, then A is convex if and only if A is an interval, possibly unbounded.

(6) If A ⊂ R

is convex and T : R

→ R

is linear, then T (A) is convex.

(7) If A ⊂ R

is convex, then any translate of A (i.e., a set of the form A + x,

x ∈ R

), is convex.

We now collect together a number of basic properties of convex and afﬁne sets.

The proof of the ﬁrst lemma is left as an exercise.

16.1.4. LEMMA. If {A

: i ∈ I} is a collection of convex subsets of R

, then

i∈I

is convex. Similarly, the intersection of a collection of afﬁne sets is afﬁne

and the intersection of a collection of cones is a cone.

16.1.5. LEMMA. If A ⊂ R

is a nonempty afﬁne set, then it is the translate of

a unique subspace of R

PROOF. Fix an element a

∈ A, and let L = {a − a

: a ∈ A}. If v = a −a

∈ L

and t ∈ R, then tv + a

= ta + (1 − t)a

∈ A. Hence tv lies in A − a

= L.

Suppose that w = b−a

is another element of L. Then since A is convex, (a+b)/2

belongs to A. Now

(v + w) + a

= a + b − a

= 2

a+b

+ (1 − 2)a

∈ A.

So v + w belongs to L. This shows that L is a subspace.

To see that L is unique, suppose that A = M + y, where M is also a subspace

of R

. Then L = A −a

= M + (y −a

). Since 0 is in L, M contains a

−y and

so M + (y − a

) = M . Therefore, L = M. ¥

16.1.6. DEFINITION. Suppose that S is a subset of R

. The convex hull of S,

denoted conv(S), is the intersection of all convex subsets of R

containing S.

The closed convex hull of S, denoted

conv(S), is the intersection of all closed

convex subsets of R

containing S.

The afﬁne hull of S, denoted aff(S), is the intersection of all afﬁne subsets of

containing S.

Let L(S) denote the unique subspace (as in Lemma 16.1.5) that is a translate

of aff(S). The dimension of S, denoted dim(S), is the dimension of L(S).

Finally, if S is a subset of R

, we use cone(S) for the intersection of all cones

containing S.

By Lemma 16.1.4, conv(S) and conv(S) are convex. Hence conv(S) is the

smallest convex set containing S. Therefore, conv(conv(S)) = conv(S). The

intersection of closed sets is closed, so conv(S) is the smallest closed convex set

containing S. Moreover, conv(conv(S)) = conv(conv(S)) = conv(S).

560 Convexity and Optimization

Likewise, aff(aff(S)) = aff(S) is the smallest afﬁne set containing S and

cone(cone(S)) = cone(S) is the smallest cone containing S. Afﬁne sets are closed

because (ﬁnite-dimensional) subspaces are closed.

Here is a useful description of the convex hull of an arbitrary set S.

16.1.7. THEOREM. Suppose that S is a subset of R

. Then a belongs to

conv(S) if and only if there are points s

, . . . , s

in S and scalars λ

, . . . , λ

[0, 1] with

i=1

= 1 so that

i=1

= a.

PROOF. We claim that

C =

i=1

: r ≥ 1, s

∈ S, λ

∈ [0, 1],

i=1

= 1

is a convex set. Consider two points of C, say a =

i=1

and b =

j=1

where the s

and t

are in S, µ

and ν

are in [0, 1], and

i=1

= 1 =

j=1

Then λa + (1 −λ)b can be written as

i=1

λµ

j=1

(1 − λ)ν

This is a linear combination of elements of S with coefﬁcients λµ

and λν

in [0, 1]

such that

i=1

λµ

j=1

(1 − λ)ν

= λ + (1 −λ) = 1.

Thus λa + (1 −λ)b also belongs to C.

Since C is convex and contains S, it follows that conv(S) is contained in C. If

we show that C is contained in conv(S), then it will follow that they are equal.

Suppose that a =

i=1

, where the λ

and s

satisfy the preceding condi-

tions. Set Λ

i=1

for 1 ≤ k ≤ r. Let k

be the smallest k for which λ

> 0.

Inductively deﬁne points a

, . . . , a

in S by a

= s

and

k−1

for k

< k ≤ r.

Since each s

belongs to S, it follows by induction that these convex combinations

all lie in conv(S). However, we also show by induction that a

i=1

for

k ≥ k

. This is evident for k = k

. Suppose that it is true for k − 1. Then

k−1

i=1

k−1

i=1

In particular, since Λ

= 1, we have a

i=1

= a lies in conv(S). ¥

16.1 Convex Sets 561

Since we are working in ﬁnite dimensions, this result may be sharpened so that

each point in the convex hull is a combination of at most n + 1 points.

16.1.8. CARATH

EODORY’S THEOREM.

Suppose that S is a subset of R

. Then each a ∈ conv(S) may be expressed as a

convex combination of n + 1 elements of S.

PROOF. By the previous proposition, a may be written as a convex combination

a =

i=1

where λ

≥ 0,

i=1

= 1, and s

∈ S, for 1 ≤ i ≤ r.

If r ≥ n + 2, we will construct another representation of a using fewer vectors

. Thus we eventually reduce this to a sum over at most n + 1 elements. We may

suppose that λ

> 0 for each i, for otherwise we reduce the list by dropping s

= 0.

Consider v

= s

− s

for 1 ≤ i < r. These are r − 1 ≥ n + 1 such vectors

in an n-dimensional space, and thus they are linearly dependent. Find constants µ

not all 0 so that

0 =

r−1

i=1

− s

) =

i=1

where µ

= −

r−1

i=1

. Let J = {i : µ

< 0}, which is necessarily nonempty. Set

δ = min{λ

/|µ

| : i ∈ J}; and pick i

so that λ

= −δµ

. Then

a =

i=1

δµ

i=1

(λ

+ δµ

By construction, the constants ν

= λ

+ δµ

≥ 0 and

i=1

= 1. Moreover,

= 0. So deleting s

from the list represents a as a convex combination of fewer

elements of S. ¥

16.1.9. COROLLARY. If A ⊂ R

is compact, then conv(A) is compact.

PROOF. Deﬁne a subset X = A

n+1

× ∆

n+1

of R

(n+1)

consisting of all points

x = (a

, a

, . . . , a

n+1

, λ

, . . . , λ

n+1

), where a

∈ A, λ

∈ [0, 1], and

n+1

i=1

= 1.

It is easy to check that X is closed and bounded and therefore is compact. Consider

the function f(x) =

n+1

i=1

. This is a continuous function from X into conv(A).

By Carath

eodory’s Theorem, f maps X onto conv(A). By Theorem 5.4.3, f(X)

is compact. Therefore, conv(A) is compact. ¥

562 Convexity and Optimization

16.1.10. DEFINITION. A hyperplane is an afﬁne set of codimension 1. Thus

a hyperplane in R

has dimension n − 1.

Hyperplanes are rather special afﬁne sets, and they serve to split the whole

space into two pieces. This is a consequence of the following result.

16.1.11. PROPOSITION. A subset H of R

is a hyperplane if and only if there

is a nonzero vector h ∈ R

and a scalar α ∈ R so that

H = {x ∈ R

: hx, hi = α}.

PROOF. If H is a hyperplane and x

∈ H, then L(H) = H − x

is a subspace of

dimension n − 1. Choose a nonzero vector h orthogonal to L(H). This is used to

deﬁne a linear map from R

into R by f (x) = hx, hi. Since the set of all vectors

orthogonal to h form a subspace of dimension n−1 containing L(H), it follows that

L(H) = {h}

⊥

= kerf.

Set α = f(x

). Then f(x) = α if and only if f(x − x

) = f(x) − α = 0,

which occurs if and only if x − x

∈ L(H) or, equivalently, when x belongs to

L(H) + x

= H.

Conversely, the linear map f(x) = hx, hi from R

into R maps onto R since

h 6= 0. Thus L(H) := kerf = {h}

⊥

is a subspace of R

of dimension n − 1.

Let x

be any vector with f(x

) = α. Then following the argument of the previous

paragraph, the set H = {x ∈ R

: hx, hi = α} = L(H) + x

is a hyperplane. ¥

Notice that the function f (or the vector h) is not unique, but it is determined up

to a scalar multiple because the subspace H

⊥

is one dimensional. When working

with a hyperplane, we will usually assume that a choice of this function has been

made. This allows us to describe two half-spaces associated to H, which we denote

by H

= {x ∈ R

: f(x) ≥ α} and H

−

= {x ∈ R

: f(x) ≤ α}. These two

subsets do not depend on the choice of f except that a sign change can interchange

with H

−

Exercises for Section 16.1

A. If A is a convex subset of R

, show that

A is convex.

B. (a) Prove Lemma 16.1.4: The intersection of convex sets is convex.

(b) State and prove the analogous result for cones and afﬁne sets.

C. Suppose that A is a closed subset of R

and whenever a, b ∈ A, the point (a + b)/2 is

in A. Show that A is convex.

HINT: Use induction to show that λa + (1 −λ)b is in A if λ = i/2

for 1 ≤ i < 2

D. If A is a convex subset of R

such that aff(A) 6= R

, show that int(A) is empty.

E. Let S be a subset of R

. Show that aff(S) =

i=1

: s

∈ S, λ

∈ R,

i=1

= 1

and L(S) =

i=1

: s

∈ S, λ

∈ R,

i=1

= 0