Давнис В.В., Тинякова В.И. Компьютерный практикум по эконометрическому моделированию
Подождите немного. Документ загружается.


Министерство образования РФ
Воронежский государственный университет
К О М П Ь Ю Т Е Р Н Ы Й П Р А К Т И К У М
ПО
ЭКОНОМЕТРИЧЕСКОМУ МОДЕЛИРОВАНИЮ
Для студентов, обучающихся по специальностям
060200 «Экономика труда»,
060600 «Мировая экономика»,
061800 «Математические методы в экономике»
Воронеж-2003
Утверждено научно-методическим советом экономического факультета
протокол № 6 от 26 июня 2003г.
Составители:
Давнис Валерий Владимирович
Тинякова Виктория Ивановна
Редактор Бунина Т.Д.
Компьютерный практикум подготовлен на кафедре информацион -
ных технологий и математических методов в экономике экономического
факультета Воронежского государственного университета. Рекоменду-
ется для студентов 3 курса дневного и вечернего отделений экономиче-
ского факультета.
ПРЕДИСЛОВИЕ
Овладение знаниями по компьютерному моделированию является обяза -
тельным элементом изучения эконометрики. Целевое назначение данного по-
собия заключается в формировании у студентов навыков практического ис-
пользования теоретических основ эконометрического моделирования в зада-
чах анализа ситуаций экономической реальности, а также обоснования про -
гнозных решений.
В пособие включены компьютерные задания по базовым темам универ-
ситетского курса «Эконометрика». Материал каждой темы содержит спра -
вочную информацию по расчетным формулам, используемым при выполне-
нии заданий. Сами задания предусматривают не только оценку параметров
модели, но и содержательную интерпретацию результатов эконометрического
моделирования. Для лучшего понимания и усвоения студентами теоретиче-
ских положений изучаемого курса в практикуме приведены примеры выпол -
нения типовых задач, а также контрольные задания для самостоятельной ра -
боты.
Задания практикума могут выполняться как с использованием Excel, так
и любого статистического (STATISTIKA, SPSS) или эконометрического паке-
та (EVeiws, STATA). Однако авторы предусмотрели выполнение компьютер-
ных типовых задач в среде табличного процессора Excel. По их мнению , это
позволяет , с одной стороны, «прочувствовать» все детали и тонкости изучае-
мых методов, что естественным образом повышает уровень усваиваемости
учебного материала, а с другой – совершенствует навыки работы в пакете Ex-
cel, являющемся тем программным продуктом, в котором современный эко-
номист проводит основную массу своих расчетов.
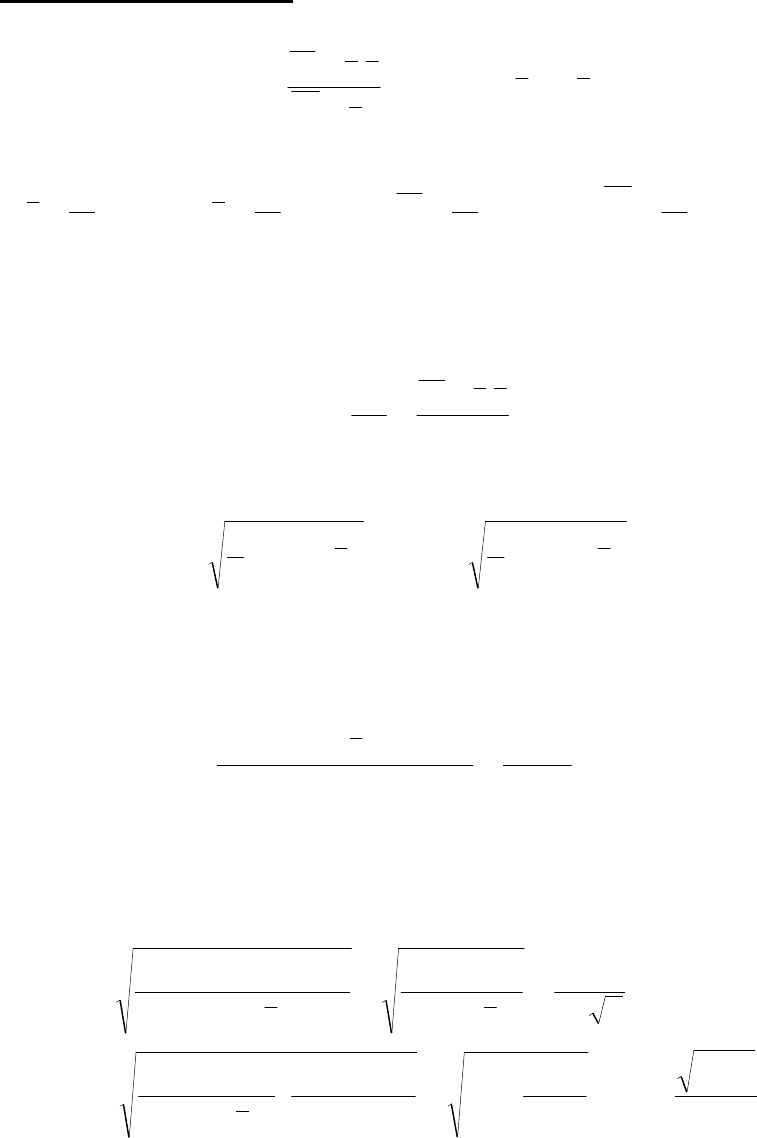
1. ОДНОФАКТОРНЫЕ РЕГРЕССИОННЫЕ МОДЕЛИ
И МЕТОД ИХ ПОСТРОЕНИЯ
1.1. Расчетные формулы
1.1.1. Оценки коэффициентов однофакторной регрессионной модели:
22
1
ˆ
x
x
yxxy
b
−
−
= , xbyb
1
0
ˆ
ˆ
−= ,
где
∑
=
=
N
i
i
x
N
x
1
1
,
∑
=
=
N
i
i
y
N
y
1
1
,
i
N
i
i
yx
N
xy
∑
=
=
1
1
,
∑
=
=
N
i
i
x
N
x
1
22
1
,
x
- независимая переменная,
y
- зависимая переменная,
N
- число элементов
выборочной совокупности.
1.1.2. Коэффициент корреляции:
yxy
x
xy
yxxy
br
σσσ
σ −
==
1
,
где
x
σ
,
y
σ
- среднеквадратические ошибки, вычисляемые по формулам
2
2
1
xx
n
i
x
−=
∑
σ ,
∑
−=
22
1
yy
n
iy
σ .
1.1.3. Коэффициент детерминации:
2
r
D
=
.
1.1.4. Дисперсионное отношение Фишера (F-критерий):
)2(
1)1(/)
ˆ
(
/)
ˆ
(
2
2
2
2
−
−
=
−−−
−
=
∑
∑
n
r
r
mnyy
myy
F
xy
xy
расч
,
где
y
ˆ
– расчетное значение зависимой переменной ( xbby
1
0
ˆ
ˆ
ˆ
+= ),
n
– число
элементов выборочной совокупности,
m
– число факторов.
1.1.5. Стандартные ошибки параметров линейной регрессии:
n
S
xx
S
xx
nyy
s
x
остост
b
σ
=
−
=
−
−−
=
∑∑
∑
2
2
2
2
)()(
)2(/)
ˆ
(
1
,
x
ост
x
остb
n
x
S
n
x
S
n
yy
xxn
x
s
σ
σ
∑
∑∑
∑
∑
==
−
−
⋅
−
=
2
22
2
2
2
2
2
)2(
)
ˆ
(
)(
0
,
где
2
ост
S – остаточная дисперсия, рассчитываемая по формуле
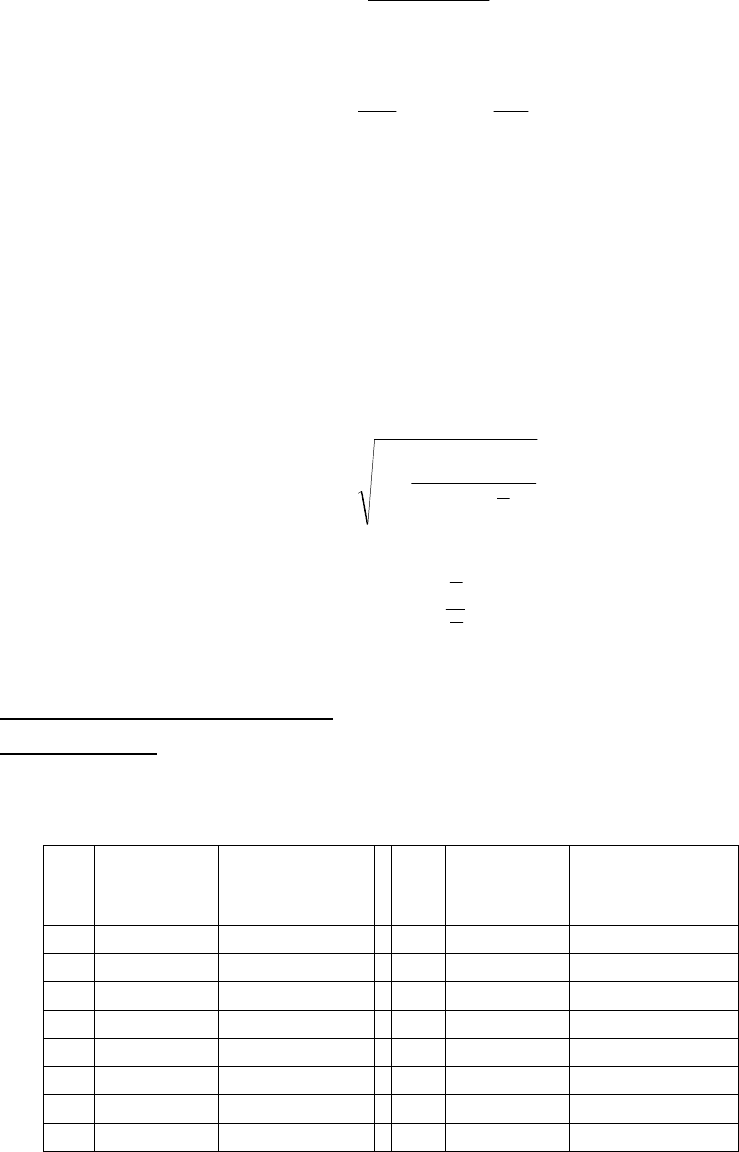
(
)
1
ˆ
2
2
−
−
−
=
∑
m
n
yy
S
ост
.
1.1.6. t-статистики Стьюдента:
0
0
0
b
b
s
b
t =
,
1
1
1
b
b
s
b
t =
.
1.1.7. Доверительные интервалы:
00
000
ˆ
ˆ
bb
bbb ∆+≤≤∆−
,
11
111
ˆ
ˆ
bb
bbb ∆+≤≤∆−
,
где
0
b
∆
,
1
b
∆
– предельные ошибки, рассчитываемые по формулам
00
b таблb
st
=
∆
,
11
b таблb
st
=
∆
,
табл
t
– табличное значение t-статистики.
1.1.8. Индекс корреляции:
∑
∑
−
−
−=
2
2
)(
)
ˆ
(
1
yy
yy
p
xy
.
1.1.9. Усредненное значение коэффициента эластичности:
y
x
bE ⋅=
1
ˆ
.
1.2. Решение типовых задач
Задание 1.2.1. По данным табл . 1.2.1 построить линейное уравнение рег-
рессии, отражающее зависимость стоимости квартиры от ее жилой площади.
Таблица 1.2.1
№
п.п.
Стоимость
(долл.)
Жилая
площадь
(кв. м .)
№
п.п
Стоимость
(долл.)
Жилая
площадь
(кв. м .)
1.
5000
30,2
9
.
5740
33
2.
5200
32
10
.
5570
31
3.
5350
32
11
.
5530
30
4.
5880
37
12
.
6020
34
5.
5430
30
13
.
7010
38
6.
5430
30
14
.
6420
31
7.
5430
30
15
.
7150
39
8.
5350
29
16
.
7190
39,5
Для построенного уравнения вычислить
1) коэффициент корреляции;
2) коэффициент детерминации;
3) дисперсионное отношение Фишера ;
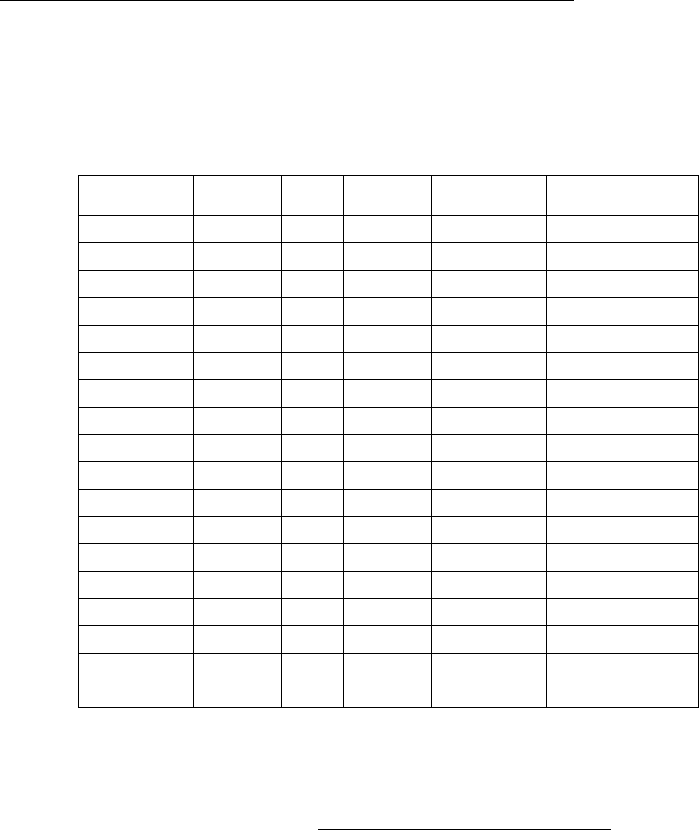
4) стандартные ошибки коэффициентов регрессии;
5) t-статистики Стьюдента;
6) доверительные границы коэффициентов регрессии.
Дать содержательную интерпретацию коэффициента регрессии постро -
енной модели. Все расчеты провести в Excel с использованием выше приве-
денных формул и «Пакета анализа». Результаты, полученные по формулам
и с помощью «Пакета анализа», сравнить между собой.
Решение с помощью табличного процессора Excel.
1. Ввод исходных данных.
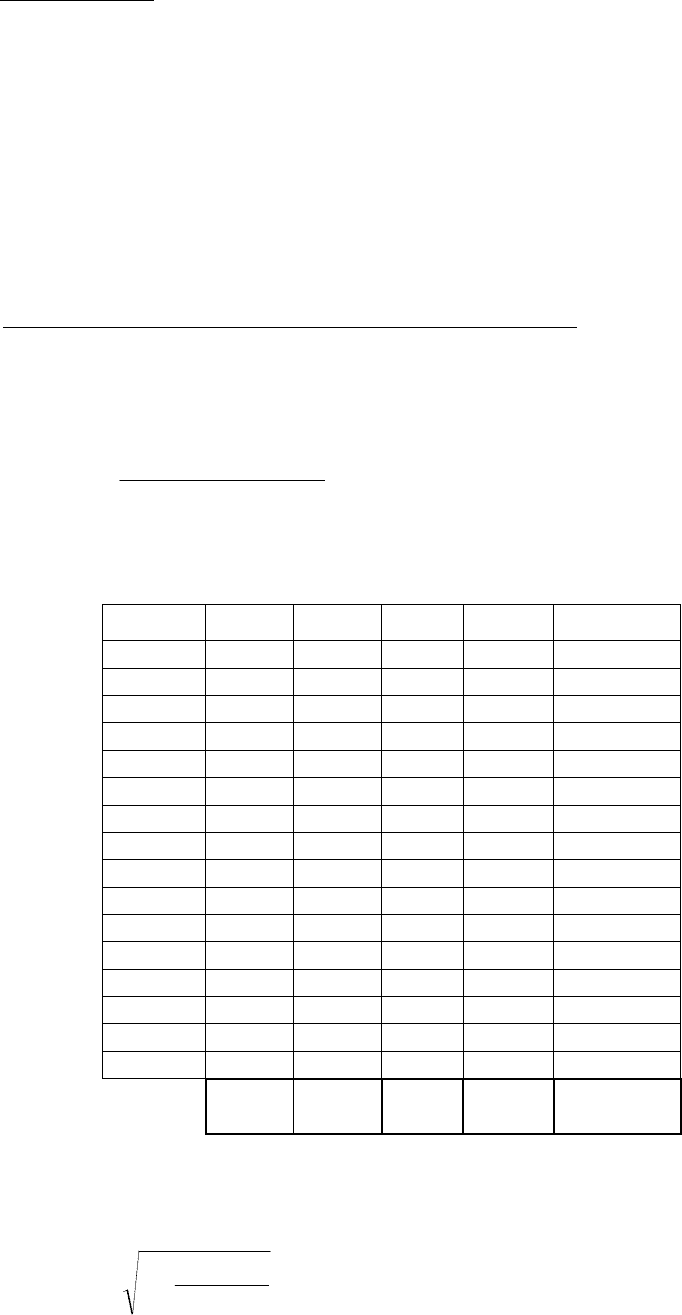
2. Подготовка данных и оформление их в виде табл . 1.2.2 для расчета
оценок коэффициентов регрессии.
Таблица 1.2.2
№ п.п. y x
2
x
xy
2
y
1.
5000
30,2
912,04
151000
25000000
2.
5200
32
1024
166400
27040000
3.
5350
32
1024
171200
28622500
4.
5880
37
1369
217560
34574400
5.
5430
30
900
162900
29484900
6.
5430
30
900
162900
29484900
7.
5430
30
900
162900
29484900
8.
5350
29
841
155150
28622500
9.
5740
33
1089
189420
32947600
10.
5570
31
961
172670
31024900
11.
5530
30
900
165900
30580900
12.
6020
34
1156
204680
36240400
13.
7010
38
1444
266380
49140100
14.
6420
31
961
199020
41216400
15.
7150
39
1521
278850
51122500
16.
7190
39,5
1560,3
284005
51696100
Среднее
значение 5856,25
32,86
1091,39
194433,44
34767688,50
3. Расчет коэффициентов регрессии:
239,170
86,3239,1091
25,585686,3244,194433
2
1
=
−
⋅
−
=b
;
847,26286,32239,17025,5856
0
=
⋅
−
=
b .
Построенная модель может быть записана в следующем виде:
x
y
239
,
170
847
,
262
+
=
.

Коэффициент регрессии
1
b этой модели показывает , что в среднем уве-
личение полезной площади на 1 кв. м . приводит к увеличению ее стоимости
на 170,24 долл.
4. Расчет коэффициента корреляции и детерминации
444,386,3239,1091
2
=−=
x
σ
; 040,68725,585650,34767688
2
=−=
y
σ ;
853,0
040,687
444,3
239,170 =⋅= r
; %818,72%100853,0
2
=⋅= D .
Коэффициент корреляции достаточно высокий, что свидетельствует о
существенной зависимости стоимости квартир от полезной площади. Коэф -
фициент детерминации показывает , что величина стоимости квартиры объяс-
няется величиной полезной площади только на 72,82 %.
5. Расчет дисперсионного отношения Фишера
504,3714
)853,01(
853,0
2
2
=⋅
−
=
расч
F .
Сравнение расчетного значения F-критерия с табличным
60,4
14;1
=
F
для
95%-ного уровня значимости позволяет сделать вывод об адекватности по-
строенной модели.
6. Расчет стандартных ошибок по формулам (1.1.5), в которых использу -
ется средняя квадратическая ошибка
ост
S , вычисленная в соответствии с
данными табл . 1.2.3.
356,918
16444,3
29,17462933,382
0
=
⋅
⋅
=
b
s ; 798,27
16444,3
933,382
1
=
⋅
=
b
s .
7. Расчет доверительных границ для коэффициентов уравнения регрессии
691
,1969356,9181448,2
0
=
⋅
=
∆
b
;
622,59798,271448,2
1
=
⋅
=
∆
b
;
691,1969847,262691,1969847,262
0
+
≤
≤
−
b ;
538,2232691,1706
0
≤
≤
−
b ;
622,59239,170622,59239,170
1
+
≤
≤
−
b ;
861,229616,110
1
≤
≤
b .
8. Построение линейного уравнения регрессии и расчет всех его характе-
ристик с помощью «Пакета анализа» табличного процессора Excel. Сравне-
ние результатов, полученных с помощью расчетных формул, с результатами
применения инструментальных средств Excel (см . Вывод итогов к заданию
1.2.1) показывает их полную идентичность, что свидетельствует о правиль-
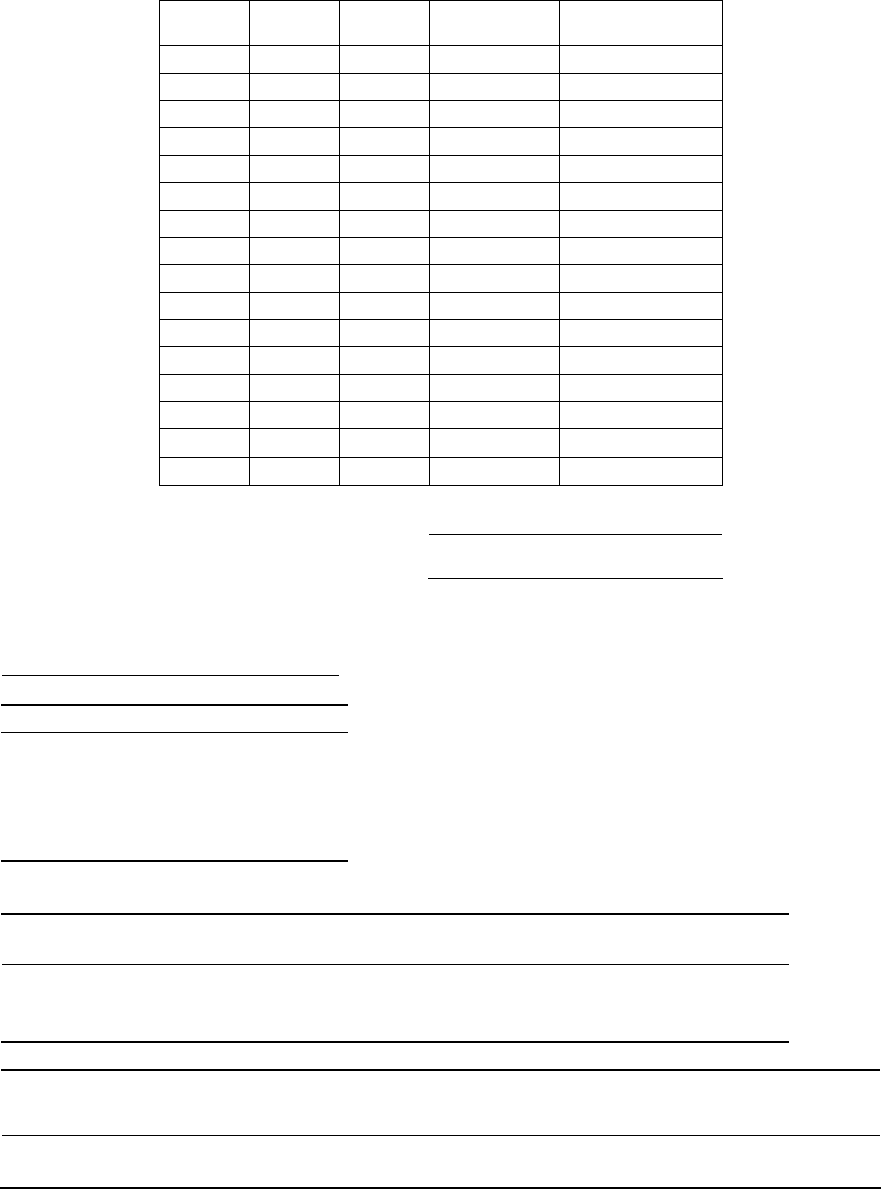
ном понимании метода построения линейных регрессионных уравнений и ме-
тодики оценки его качества .
Таблица 1.2.3
№ п/п y x
y
ˆ
(
)
2
ˆ
yy −
1.
5000
30,2
5404,054
163259
2.
5200
32
5710,483
260593
3.
5350
32
5710,483
129948
4.
5880
37
6561,676
464683
5.
5430
30
5370,006
3599
6.
5430
30
5370,006
3599
7.
5430
30
5370,006
3599
8.
5350
29
5199,767
22570
9.
5740
33
5880,722
19803
10.
5570
31
5540,245
885
11.
5530
30
5370,006
25598
12.
6020
34
6050,96
959
13.
7010
38
6731,915
77331
14.
6420
31
5540,245
773970
15.
7150
39
6902,154
61428
16.
7190
39,5
6987,273
41098
(
)
2
ˆ
∑
− yy
2052923
ост
S
382,933
ВЫВОД ИТОГОВ к заданию 1.2.1
Регрессионная статистика
Множественный R 0,853
R-квадрат 0,728
Нормированный R-квадрат
0,709
Стандартная ошибка 382,933
Наблюдения 16
Дисперсионный анализ
df SS MS F
Значи -
мость F
Регрессия 1
5499452,368
5499452,368
37,504
0,00003
Остаток 14
2052922,632
146637,331
Итого 15
7552375
Коэффи-
циенты
Стандартная
ошибка
t-
статистика
P-
Значе -
ние
Нижние
95%
Верхние
95%
Y-пересечение 262,847
918,356
0,286
0,779
-1706,833
2232,528
Переменная X 1 170,239
27,798
6,124
0,000
110,617
229,860
Задание 1.2.2. По данным табл . 1.2.1 построить нелинейное уравнение
регрессии в виде показательной функции, отражающее зависимость стоимости
квартиры от ее полезной площади. Для построенного уравнения вычислить :
1) индекс корреляции;
2) коэффициент детерминации;
3) дисперсионное отношение Фишера .
Дать содержательную интерпретацию коэффициента регрессии постро -
енной модели. Все расчеты провести в Excel с использованием выше приве-
денных формул.
Решение с помощью табличного процессора Excel.
1. Ввод исходных данных.
2. Подготовка данных и оформление их в виде табл . 1.2.4 для расчета ко-
эффициентов регрессии.
028,0
33
1091
669,833151,285
2
1
=
−
⋅
−
=Lnb ; 761,733028,0669,8
0
=
⋅
−
=
Lnb ;
028,1718,2
028,0
1
1
===
Lnb
eb ; 862,2347718,2
761,7
0
0
===
Lnb
eb .
Таблица 1.2.4
№ п/п y
y
ln
x
2
x
y
x
ln
1.
5000
8,517
30,2
912,04
257,2192
2.
5200
8,556
32
1024
273,8052
3.
5350
8,585
32
1024
274,7153
4.
5880
8,679
37
1369
321,1345
5.
5430
8,600
30
900
257,9908
6.
5430
8,600
30
900
257,9908
7.
5430
8,600
30
900
257,9908
8.
5350
8,585
29
841
248,9607
9.
5740
8,655
33
1089
285,6221
10.
5570
8,625
31
961
267,3797
11.
5530
8,618
30
900
258,5383
12.
6020
8,703
34
1156
295,8966
13.
7010
8,855
38
1444
336,4935
14.
6420
8,767
31
961
271,7824
15.
7150
8,875
39
1521
346,1198
16.
7190
8,880
39,5
1560,25
350,7776
Среднее
значение
58568,669
33
1091
285,151
3. Расчет индекса корреляции и коэффициента детерминации с оформле-
нием промежуточных вычислений в виде табл . 1.2.5.
859,0
7552375
1975343
1 =−=
xy
p ; %84,73%100859,0
2
=⋅= D .
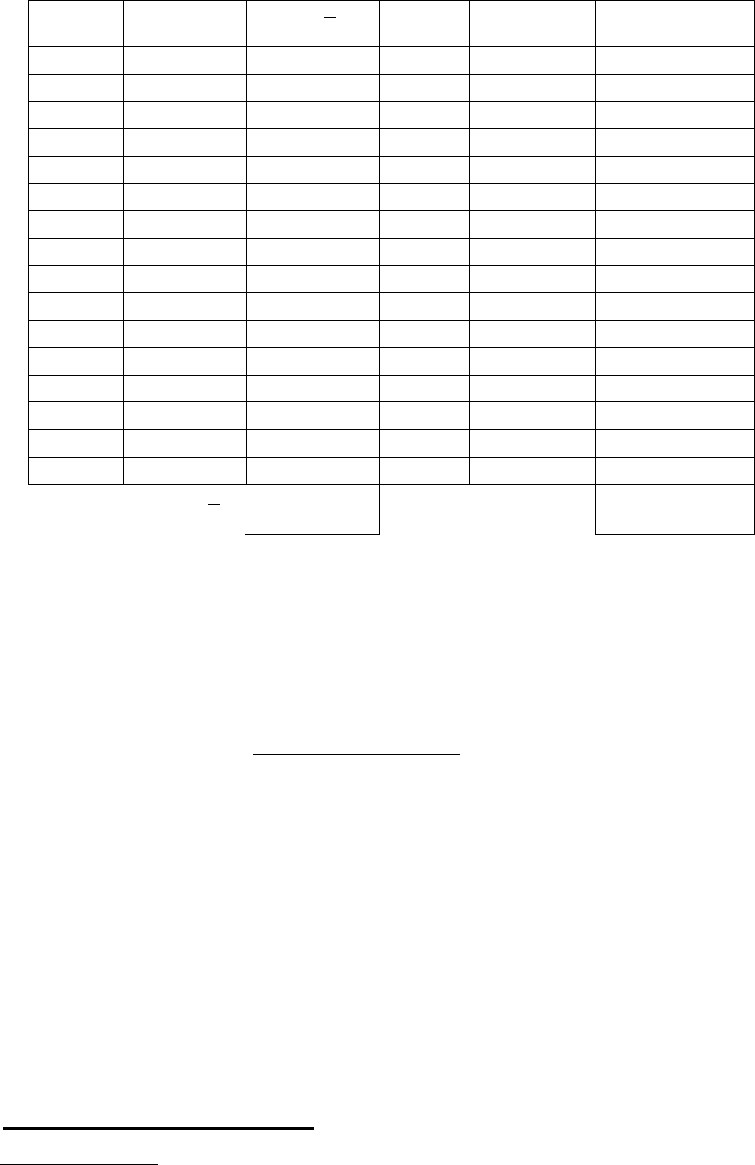
Таблица 1.2.5
№ п/п y
(
)
2
yy −
x
y
ˆ
(
)
2
ˆ
yy −
1.
5000
733164,1
30,2
5406,783
165472
2.
5200
430664,1
32
5682,389
232699
3.
5350
256289,1
32
5682,389
110482
4.
5880
564,0625
37
6523,923
414636
5.
5430
181689,1
30
5376,997
2809
6.
5430
181689,1
30
5376,997
2809
7.
5430
181689,1
30
5376,997
2809
8.
5350
256289,1
29
5230,512
14277
9.
5740
13514,06
33
5841,529
10308
10.
5570
81939,06
31
5527,584
1799
11.
5530
106439,1
30
5376,997
23410
12.
6020
26814,06
34
6005,125
221
13.
7010
1331139
38
6706,63
92033
14.
6420
317814,1
31
5527,584
796406
15.
7150
1673789
39
6894,455
65303
16.
7190
1778889
39,5
6990,331
39868
(
)
∑
−
2
yy
7552375
(
)
2
ˆ
∑
− yy
1975343
При использовании показательной зависимости изменения стоимости
квартиры объясняются соответствующими изменениями полезной площади
на 73,84%.
4. Расчет дисперсионного отношения Фишера
527,3914
1975343
19753437552375
=⋅
−
=
расч
F .
Сравнение расчетного значения F-критерия с табличным
60,4
14;1
=
F
для
95%-ного уровня значимости позволяет сделать вывод об адекватности по-
строенной модели.
5. Построенная регрессионная модель в виде показательной функции
x
y 028,1862,2347 ⋅= ,
позволяет утверждать, что в среднем увеличение полезной площади на 1
кв.м . повышает стоимость квартиры в 1,028 раза .
1.3. Контрольные задания
Задание 1.3.1. По данным табл . 1.3.1 построить линейные уравнения рег-
рессии, отражающие зависимость стоимости подержанных автомобилей мо-
делей ВАЗ 2105 и ВАЗ 2107 от срока их эксплуатации. Для построенных
уравнений вычислить:
