Денискина Е.А., Коломиец П.Э. (сост) Статистический анализ данных
Подождите немного. Документ загружается.

21
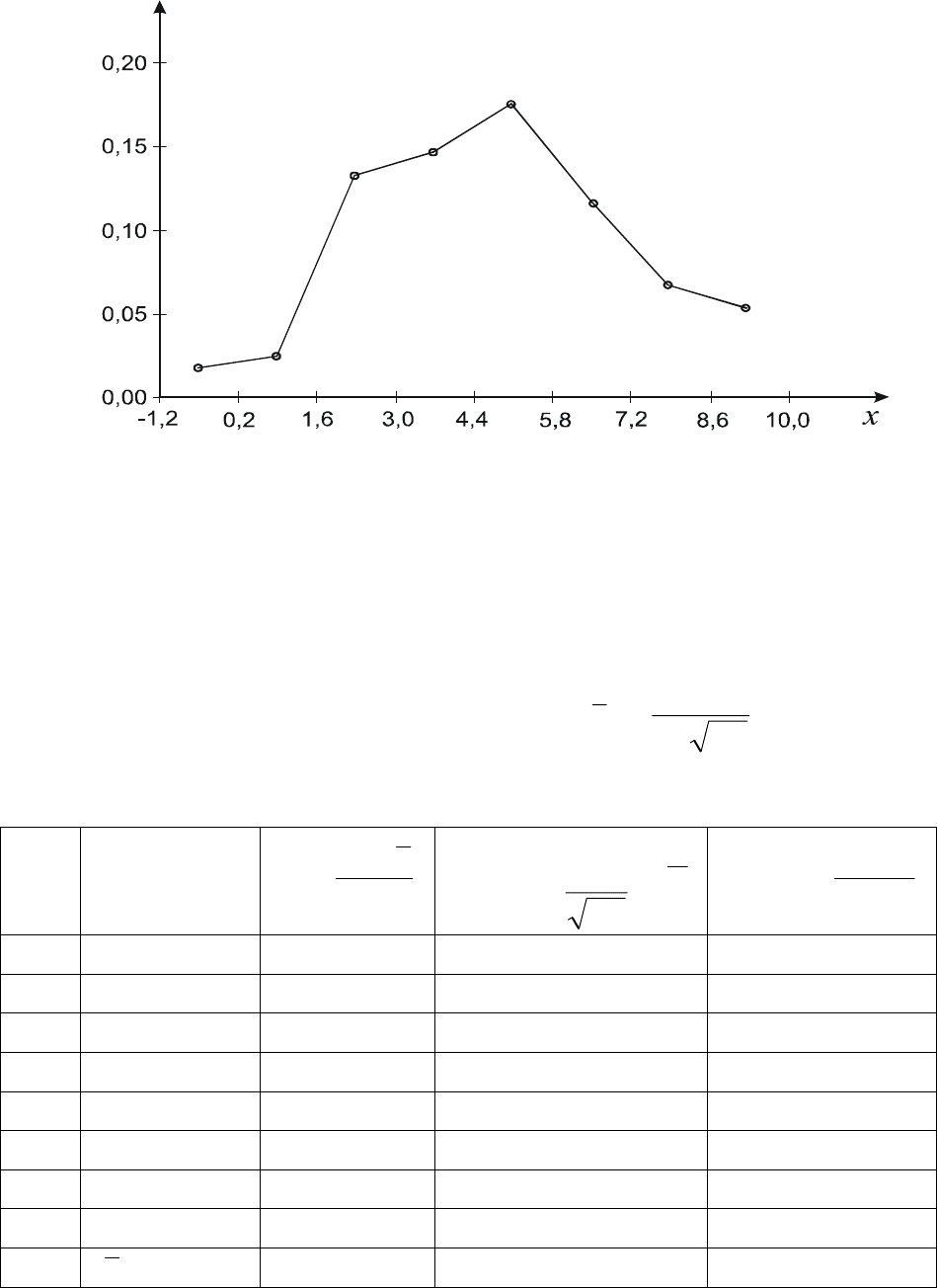
Рис. 4
Полигон относительных частот
Вычислим значения теоретической плотности вероятностей в точках
i
z –
середины интервалов по таблице П 2 Приложения. Результаты вычислений
занесем в таблицу 8. Заметим, что
1761,0
2
1
)()(
0
max
===
π
S
xfxf
.
Таблица 8
i
i
z
0
S
xz
t
i
i
−
=
2
0
2
2
1
)(
i
t
i
etf
−
=
π
0
0
)(
)(
S
tf
zf
i
i
=
1
-0,5 -2,4258 0,0210 0,0093
2
0,9 -1,8079 0,0778 0,0344
3
2,3 -1,1900 0,1965 0,0867
4
3,7 -0,5721 0,3387 0,1495
5
5,1 0,0459 0,3985 0,1759
6
6,5 0,6638 0,3201 0,1413
7
7,9 1,2817 0,1755 0,0774
8
9,3 1,8996 0,0657 0,0290
9961,4=
x
0,0000 0,3989 0,1761
h

22
Последний столбец таблицы 8 можно вычислить сразу по серединам
интервалов
i
z
с помощью статистической функции НОРМРАСП пакета
EXCEL с логическим значением ЛОЖЬ.
Для построения теоретической плотности вероятностей на рисунке 3
поставим точки
))(;(
ii
zfz
,
Ni ,1=
и ))(,(
x
f
x
и соединим их плавной
линией. Из рисунка 3 видно, что график теоретической плотности вероятностей
и гистограмма достаточно хорошо совпадают.
1.5. ЭМПИРИЧЕСКАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ
Пусть
{
}
kn
xxxX ,,,
21
K=
– выборка объема n , содержащая
k
различных вариант, из генеральной совокупности случайной величины
X ,
имеющая функцию распределения
)(
x
F
,
ℜ
∈
x
.
Неизвестную функцию распределения генеральной совокупности
)(
x
F
называют теоретической функцией распределения.
Эмпирической функцией распределения группированной выборки
n
X
называется функция
)( xF
n
, определяющая для любого
ℜ
∈
x
относительную
частоту события
)(
x
X < , то есть
∑
<
=
xz
in
i
nxF )(
, где
2
1+
+
=
ii
i
uu
z
–
середины интервалов группировки;
i
n
– относительные частоты тех
интервалов, середины которых меньше
x
.
По определению
)( xF
n
зависит от выборки и обладает свойствами
функции распределения случайной величины. В частности
)( xF
n
:
1. неубывающая функция;
2. непрерывная слева;
3. имеет значения, принадлежащие отрезку
[
]
1,0 ;
4. при
1
zx ≤ 0)( =xF
n
, а при
N
zx > 1)(
=
xF
n
.

23
Различие между эмпирической и теоретической функциями состоит в
том, что теоретическая функция
)(
x
F
определяет вероятность события
)(
x
X
< , а эмпирическая функция )( xF
n
определяет относительную частоту
этого же события, найденную по данной выборке.
Значение эмпирической функции распределения для статистики
определяется следующим утверждением.
Теорема (Гливенко): Пусть
)( xF
n
– эмпирическая функция
распределения, построенная по выборке объема
n из генеральной
совокупности с функцией распределения
)(
x
F
. Тогда для любого
ℜ
∈
x
и
0>
ε
()
1)()(lim =<−
∞→
ε
xFxF
n
n
P
.
Таким образом, при каждом
x
)( xF
n
сходится по вероятности к )(
x
F
и, следовательно, при большом объеме выборки может служить приближенным
значением (оценкой) функции распределения генеральной совокупности в
каждой точке
x
.
Обычно эмпирическую функцию распределения
)( xF
n
группированной
выборки записывают в виде:
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
<=
≤<
≤<
≤
=
.,1
,,
,,
,,0
)(
322
211
1
xzw
zxzw
zxzw
zx
xF
NN
n
K
,
где
i
w
(
)
Ni ,1= – накопленные относительные частоты (таблица 4).
График эмпирической функции распределения
)( xF
n
имеет
ступенчатый вид (рис. 5).
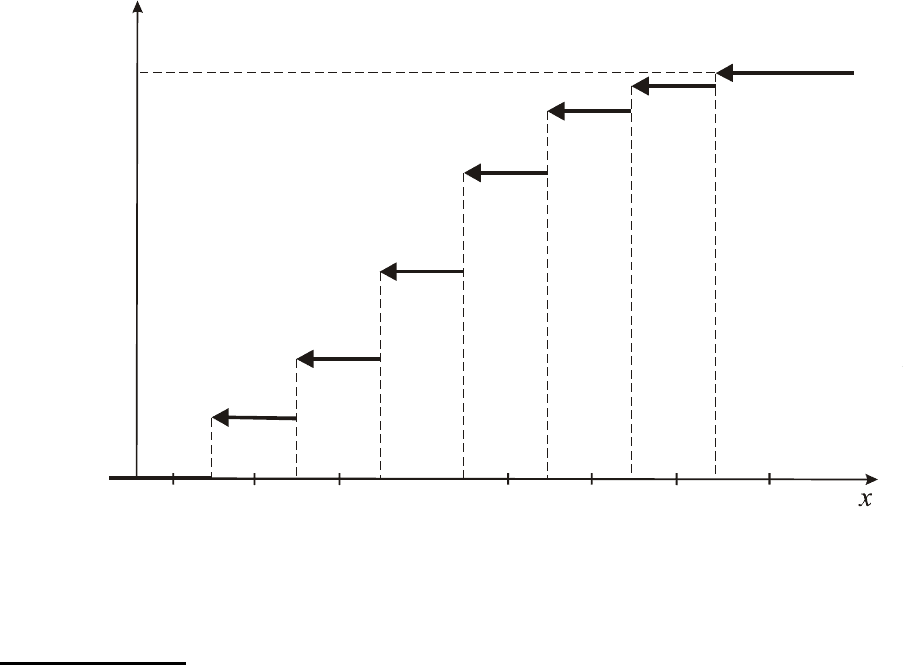
24
Рис. 5
Эмпирическая функция распределения
П Р И М Е Р 4 (пункты 6 и 7 части 1 Задания):
Требуется составить эмпирическую функцию распределения
)( xF
n
группированной выборки (таблица 6) и построить ее график. На одном чертеже
с эмпирической функцией распределения построить график теоретической
функции распределения. Сделать вывод об их визуальном совпадении.
Взяв значения накопленных относительных частот из таблицы 6, а
значения середин интервалов из таблицы 7, составим эмпирическую функцию
распределения и построим ее график (рис. 6):
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=
>
≤<
≤<
≤<
≤<
≤<
≤<
≤<−
−≤
.3,9,0000,1
,3,99,7,9293,0
,9,75,6,8384,0
,5,61,5,6768,0
,1,57,3,4343,0
,7,33,2,2323,0
,3,29,0,0505,0
,9,05,0,0202
,0
,5,0,0000,0
)(
x
x
x
x
x
x
x
x
x
xF
n
.
1
u
2
u
3
u
i
u
1
+
i
u
N
u
1
+
N
u
1
z
2
z
i
z
N
z
1
)(
xF
n
25
Согласно выдвинутой гипотезе о виде распределения генеральной
совокупности, теоретическая функция распределения генеральной
совокупности является функция распределения нормального закона:
2
2
()
2
0
11
()
2
2
tm
x
xm
Fx e dt
σ
σ
σπ
−
−
−∞
−
⎛⎞
=
=Φ +
⎜⎟
⎝⎠
∫
,
где
2
2
0
0
1
()
2
u
t
tedu
π
−
Φ=
∫
– функция Лапласа. Здесь, как и ранее,
4,9961mx== , 2657,2
0
=
=
S
σ
.
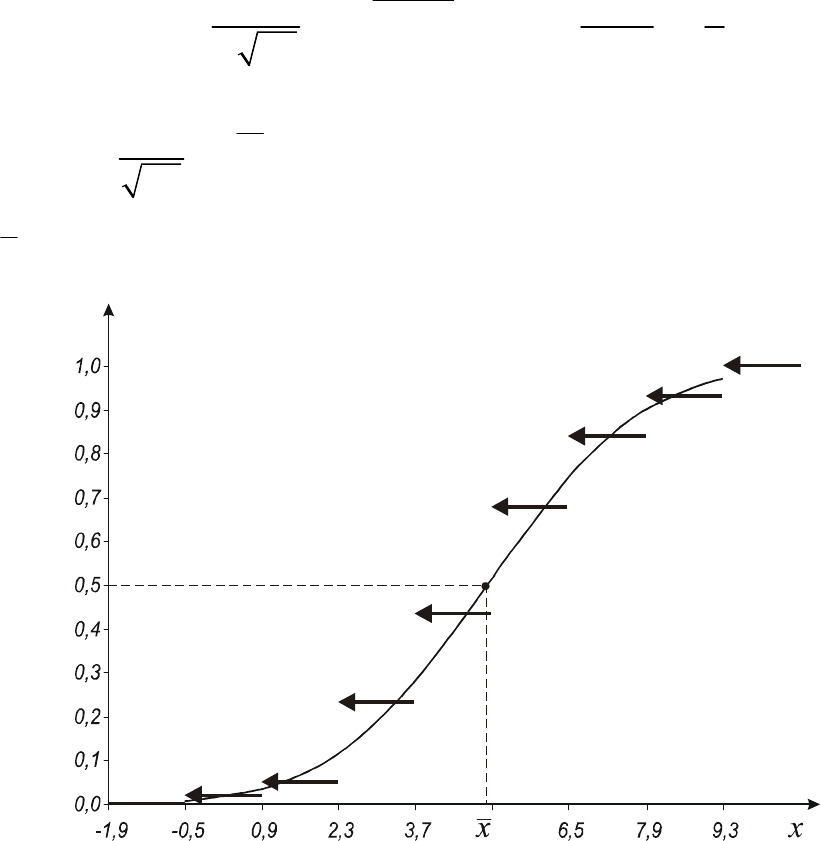
Рис. 6
Эмпирическая и теоретическая функции распределения
На одном чертеже с эмпирической функцией распределения построим
график теоретической функции распределения. Для этого найдем значения
теоретической функции распределения в точках
i
z . Для удобства вычислений
значений теоретической функции распределения заполним таблицу 9.
)(
x
F
n
)(
x
F

26
Значения функции Лапласа
)(
0 i
t
Φ
, по которой вычисляются значения
функции распределения
()
i
Fz , приведены в таблице П 1 Приложения.
Значения функции распределения
()
i
Fz
в точках
i
z
можно также найти
с помощью пакета прикладных программ EXCEL, используя статистическую
функцию НОРМРАСП с логическим значением ИСТИНА.
Таблица 9
i
i
z
0
i
i
zx
t
S
−
=
)(
0 i
t
Φ
0
1
() ()
2
ii
Fz t=Φ +
1
-0,50 -2,4258 -0,4924 0,0076
2
0,90 -1,8079 -0,4649 0,0351
3
2,30 -1,1900 -0,3830 0,1170
4
3,70 -0,5720 -0,2157 0,2843
5
5,10 0,0459 0,0160 0,5160
6
6,50 0,6638 0,2454 0,7454
7
7,90 1,2817 0,3997 0,8997
8
9,30 1,8997 0,4713 0,9713
9961,4=
x
0,0000 0,0000 0,5000
График теоретической функции распределения строим на рисунке 6 по
второму и пятому столбцам таблицы 9, соединив точки плавной линией.
Заметим, что точка перегиба кривой теоретической функции распределения
имеет координаты
()
5,0;x .
Сравнивая графики
)( xF
n
и )(
x
F
(рис. 6) можно сделать вывод, что
)( xF
n
является статистическим аналогом )(
x
F .
1.6. РАСПРЕДЕЛЕНИЯ
2
χ
И СТЬЮДЕНТА
Рассмотрим некоторые виды специальных распределений, используемых
в математической статистике. Сначала введем определение:
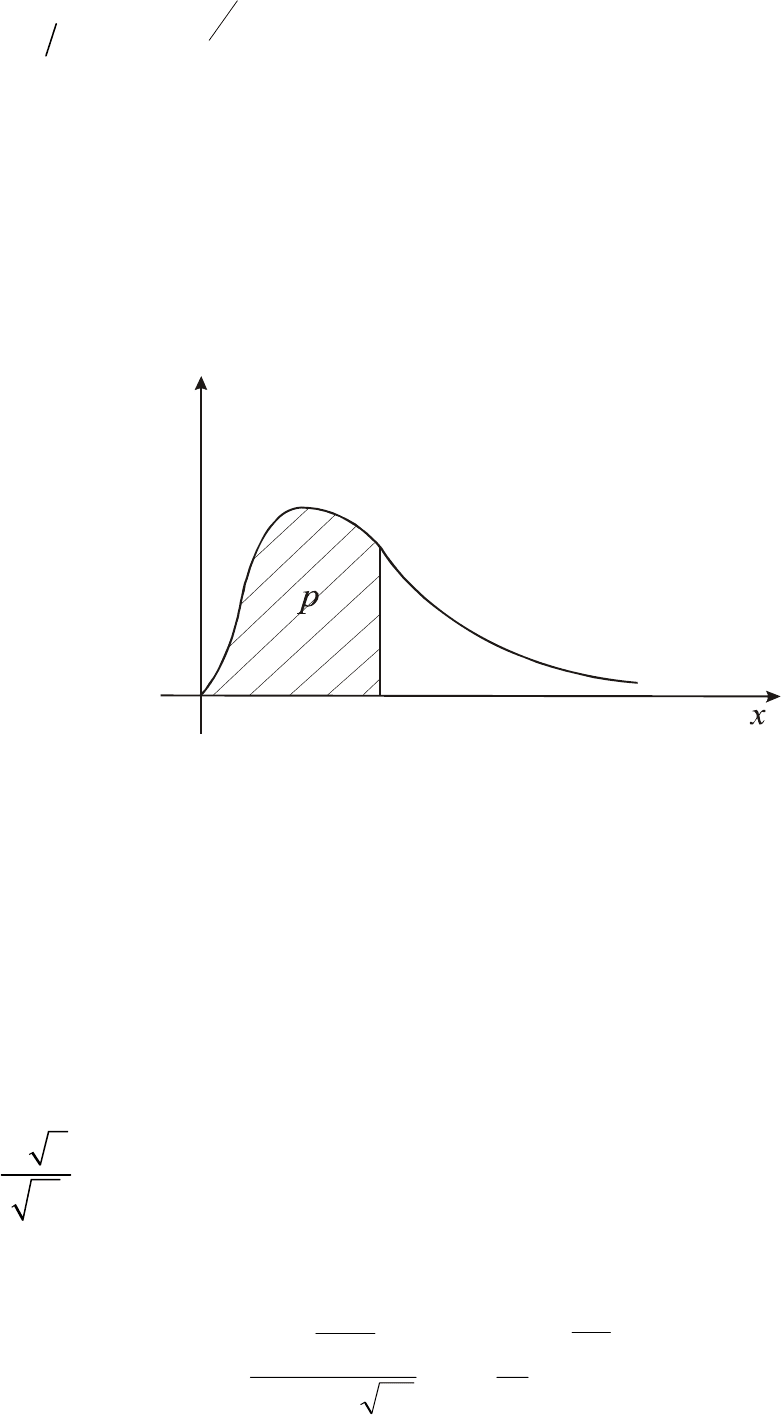
Квантилью, соответствующей вероятности
p , называется такое
значение
p
x , при котором выполняется соотношение:
27
()
∫
∞
−
==<
p
x
p
pdxxfxXP )(
,
где
()
xf – плотность вероятностей соответствующего закона распределения
(слово квантиль – женского рода). Геометрическое пояснение смысла квантили,
отвечающей вероятности
p
, приведено на рисунке 8.
РАСПРЕДЕЛЕНИЕ
2
χ
Пусть
k
XXX ,,,
21
K – нормально распределенные независимые
случайные величины, причем математическое ожидание каждой из них равно
нулю, а среднеквадратическое отклонение – единице, то есть
i
X
∼
(
)
1,0N .
Тогда сумма квадратов этих величин
()
∑
=
=+++=
k
i
ik
XXXXk
1
222
2
2
1
2
K
χ
распределена по закону
2
χ
(«хи квадрат») с
k
степенями свободы.
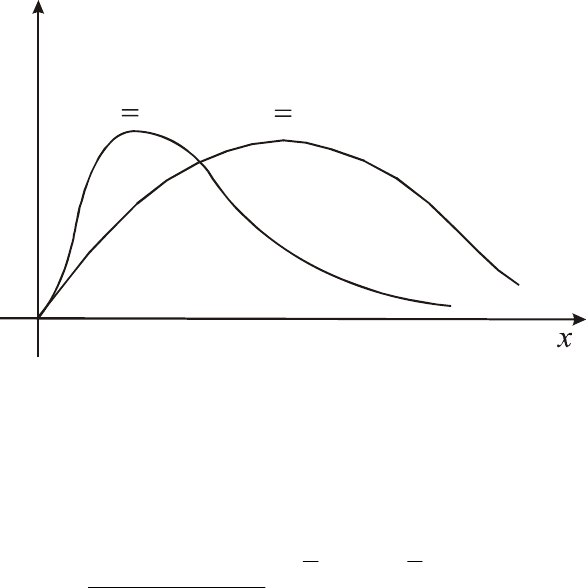
Рис. 7
Графики плотности вероятностей распределения
2
χ
Плотность вероятностей этого распределения имеет вид:
()
)0(,
2/2
1
)(
2
1
2
2/
>⋅⋅=
−−
xex
kГ
xf
xk
k
k
,
)(
xf
k
6
k
18
k
0
28
где
2
0
(2)
k
t
t
Г ketdt
∞
−
−
=⋅
∫
- гамма- функция.
График плотности вероятностей
)( xf
k
при малых
k
имеет длинный
правый «хвост», а с ростом
k
становится почти симметричным (рис. 7).
Квантили распределения
2
χ
обозначаются )(
2
kx
pp
χ
= (рис. 8) и
находятся по таблицам (таблица П 5 Приложения).
Рис. 8
Геометрическое пояснение смысла квантили
p
x
,
отвечающей вероятности
p
РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА
Пусть
U
– нормально распределенная случайная величина, причем
U
∼ )1,0(
N
, а
V
– независимая от
U
случайная величина, распределенная по
закону
2
χ
с
k
степенями свободы. Тогда известно, что случайная величина
Uk
Т
V
=
имеет
t
-распределение или распределение Стьюдента с
k
степенями свободы. Плотность вероятностей этого распределения имеет вид:
()
2
1
2
1
2/
2
1
)(
+
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+⋅
⎟
⎠
⎞
⎜
⎝
⎛
+
=
k
k
k
t
kkГ
k
Г
tf
π
(рис. 9).
)(
xf
k
0
p
x
29
При
∞→
k
распределение Стьюдента стремится к нормальному и при
30≥
k
практически не отличается от нормального )1,0(
N
.
Квантили распределения Стьюдента
p
t находят по таблицам (таблица П
4 Приложения) в зависимости от вероятности
p
и числа степеней свободы
k
.
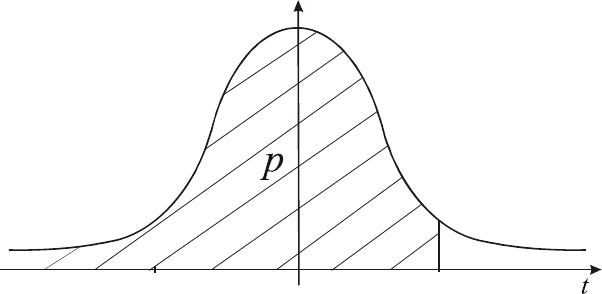
Так как график плотности вероятностей распределения Стьюдента
симметричен относительно
0=
t
, то
1pp
tt
−
=
−
(рис. 9).
Квантили распределений Стьюдента и
2
χ
можно найти с помощью
статистических функций СТЬЮДРАСПОБР и ХИ2ОБР пакета прикладных
программ EXCEL.
Рис. 9
Плотность вероятностей и квантили распределения Стьюдента
1.7. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
Для получения обоснованных выводов о параметрах, виде распределения
и других свойствах случайных величин необходимо проверить гипотезу о
соответствии эмпирической функции распределения одному из известных
теоретических законов.
Статистической гипотезой называют любое утверждение о виде или о
параметрах распределения генеральной совокупности. Например,
статистическими являются гипотезы:
1. генеральная совокупность распределена по нормальному закону или
любому другому конкретно заданному закону (гипотеза о виде распределения);
p
t
p
t
−
1
)(
tf
k
0

30
2. если известно, что генеральная совокупность распределена по
нормальному закону, то параметры нормального закона равны выборочным
характеристикам:
X
mm x
=
=
%
,
0
~
S
X
=
=
σ
σ
(параметрическая гипотеза).
Гипотезу о виде распределения выдвигают на основе схожести
гистограммы или полигона частот с соответствующей кривой одного из
теоретических законов (нормального, равномерного, Пуассона и т. п.).
Когда предположение о виде распределения генеральной совокупности
принято, следует проверить гипотезу о параметрах этого распределения.
Нулевой (основной) называют выдвинутую гипотезу
0
H .
Альтернативными называют гипотезы, которые противоречат нулевой.
Если отвергается
0
H , то принимается одна из альтернативных гипотез. При
проверке статистических гипотез могут быть допущены ошибки двух родов с
вероятностями:
1.
α
– вероятность отклонить гипотезу
0
H
, при условии, что она верна
(ошибка первого рода);
2.
β
– вероятность принять гипотезу
0
H , при условии, что она неверна
(ошибка второго рода).
Например, в радиолокации
α
– вероятность пропуска сигнала,
β
–
вероятность ложной тревоги.
Ясно, что чем меньше будут ошибки первого и второго рода, тем точнее
статистический вывод. Однако при заданном объеме выборке одновременно
уменьшить
α
и
β
невозможно. Единственный способ одновременного
уменьшения
α
и
β
состоит в увеличении объема выборки.
Если формулируется только одна гипотеза
0
H
и требуется проверить,
согласуются ли статистические данные с этой гипотезой или они ее
опровергают, то критерии, используемые для этого, называют критериями
согласия. В таких критериях не выставляется конкретная альтернативная
гипотеза.
