Денискина Е.А., Коломиец П.Э. (сост) Статистический анализ данных
Подождите немного. Документ загружается.

31
Прежде, чем привести схему статистической проверки гипотез, дадим
используемые ниже определения новых понятий.
Статистикой критерия называется специально подобранная функция
выборки
()
n
xxxKK ,,,
21
K=
, которая служит для проверки гипотезы
0
H
.
Статистика
K
является мерой расхождения экспериментальных данных с
гипотетическим распределением.
Как правило, перед анализом выборки задается уровень значимости
α
–
вероятность ошибочного отклонения нулевой гипотезы. Обычно полагают
05,0=
α
,
01,0=
α
,
001,0=
α
.
Критической областью называется совокупность значений статистики,
при которых нулевая гипотеза отвергается. Обычно критическую область
выбирают из условия
(
)
α
=
>
кр
KKP . Критическую точку критерия
кр
K
находят по соответствующим таблицам.
Схема статистической проверки гипотезы по критерию согласия:
1) формулировка нулевой
0
H
гипотезы;
2) выбор уровня значимости
α
;
3) выбор статистики
K
и соответствующего критерия;
4) определение критической области и области принятия гипотезы;
5) вычисление выборочной статистики
выб
K и проверка гипотезы;
6) принятие статистического решения.
1.8. КРИТЕРИЙ СОГЛАСИЯ
2
χ
ПИРСОНА
Для проверки гипотез о виде распределения применяются различные
критерии согласия:
2
χ
(«хи- квадрат») К. Пирсона, критерий Колмогорова,
критерий Смирнова и др. Наиболее удобным и универсальным критерием
является критерий
2
χ
Пирсона. Он совершенно не зависит ни от вида
распределения случайной величины, ни от ее размерности.

32
Ограничимся описанием применения критерия Пирсона для проверки
гипотезы о нормальном распределении генеральной совокупности (критерий
аналогично применяется и для других распределений).
Схема применения критерия согласия
2
χ
:
1). Выдвигается гипотеза
0
H
: генеральная совокупность имеет
нормальное распределение с плотностью вероятностей :
2
2
()
2
1
()
2
x
m
fx e
σ
σπ
−
−
=
с параметрами
X
mm x==
%
,
0
~
S
X
=
=
σ
σ
, то есть выборочное среднее
x
и
модифицированная выборочная дисперсия
2
0
S принимаются соответственно за
математическое ожидание
m и дисперсию
2
σ
нормально распределенной
случайной величины.
2). По выборке наблюдений случайной величины
X составляется
группированный вариационный ряд (таблица 4).
3). Вычисляются вероятности
i
p
(
)
Ni ,1=
попадания значений
случайной величины X в i -тый интервал.
Для нормального закона
()
1
1
ii
ii i
um um
pPuXu
σσ
+
+
−
−
⎛⎞⎛⎞
=<≤ =Φ −Φ
⎜⎟⎜⎟
⎝⎠⎝⎠
.
Здесь
()
x
Φ – функция распределения нормального закона (0;1)N , значения
которой находят по таблицам.
4). Вычисляется выборочное значение статистики критерия
2
χ
:
2
2
1
()
N
ii
выб
i
i
nnp
np
χ
=
−⋅
=
⋅
∑
,
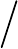
33
где
N
– число интервалов разбиения выборки; n – объем выборки;
i
n –
частота
i -того интервала;
i
p – теоретическая вероятность попадания значений
случайной величины
X в i -тый интервал.
К. Пирсон доказал, что эта статистика независимо от вида распределения
генеральной совокупности при
∞
→n имеет
2
χ
- распределение с
1−−=
s
N
q степенями свободы, где
N
– число интервалов разбиения,
s
–
число оцениваемых параметров гипотетического закона распределения. Для
нормального закона
2=
s
(параметры m и
σ
).
5). Областью отклонения
G (критической областью) гипотезы
0
H
называется такая область, при попадании в которую статистики
2
выб
χ
гипотеза
0
H
отклоняется. Область отклонения G выбирается так, чтобы вероятность
попадания в нее величины
2
выб
χ
, когда гипотеза
0
H верна, была равна уровню
значимости α. Тогда критическая точка
2
кр
χ
, ограничивающая область G ,
определяется из уравнения:
()()
2
22
0
()
кр
выб кр k
PGHPK fxdx
χ
χ
χα
+
∞
∈
=>= =
∫
.
Из этой формулы следует, что критическая точка
2
кр
χ
равна с квантили
распределения Пирсона
2
р
χ
, отвечающей вероятности
α
−= 1p с числом
степеней свободы
1−−
=
s
N
q (таблица П 5 Приложения).
Таким образом, если вычисленная выборочная статистика
[
)
22
;0
крвыб
χχ
∈ , то гипотеза
0
H принимается. Если
22
крвыб
χχ
≥ , то
гипотеза
0
H отвергается.
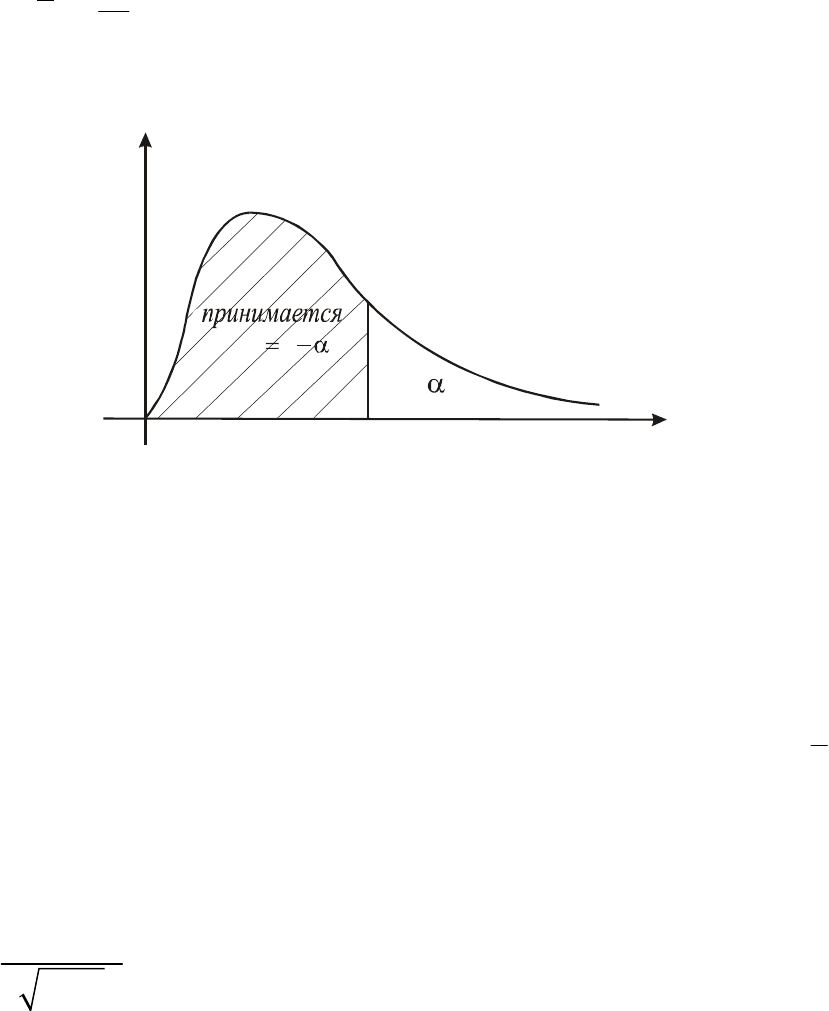
Область принятия критерия имеет вид, представленный на рис. 10.
34
Выбор области принятия гипотезы можно объяснить следующим
образом: значения теоретических вероятностей
i
p
и относительных частот
интервалов
n
n
n
i
i
= должны быть достаточно близки, поэтому разности
()
ii
nnp−⋅ не должны быть слишком велики.
Рис. 10
Область принятия критерия
Статистический вывод неверно формулировать в виде: генеральная
совокупность имеет нормальный закон распределения. Можно лишь
утверждать, что данная выборка согласуется с гипотезой о нормальном
распределении генеральной совокупности с параметрами
X
mm x==
%
,
0
~
S
X
==
σ
σ
на уровне значимости
α
.
З а м е ч а н и е: критерий
2
χ
использует тот факт, что случайная
величина
ii
i
nnp
np
−⋅
⋅
имеет распределение, близкое к нормальному. Чтобы это
утверждение было достаточно точным, необходимо выполнение условия
5
i
np⋅≥
для всех интервалов. Интервалы, для которых это условие не
выполняется, следует объединить с соседними.
)(
xf
k
0
0
H
1
p
.с
2
kp
χ
2
χ
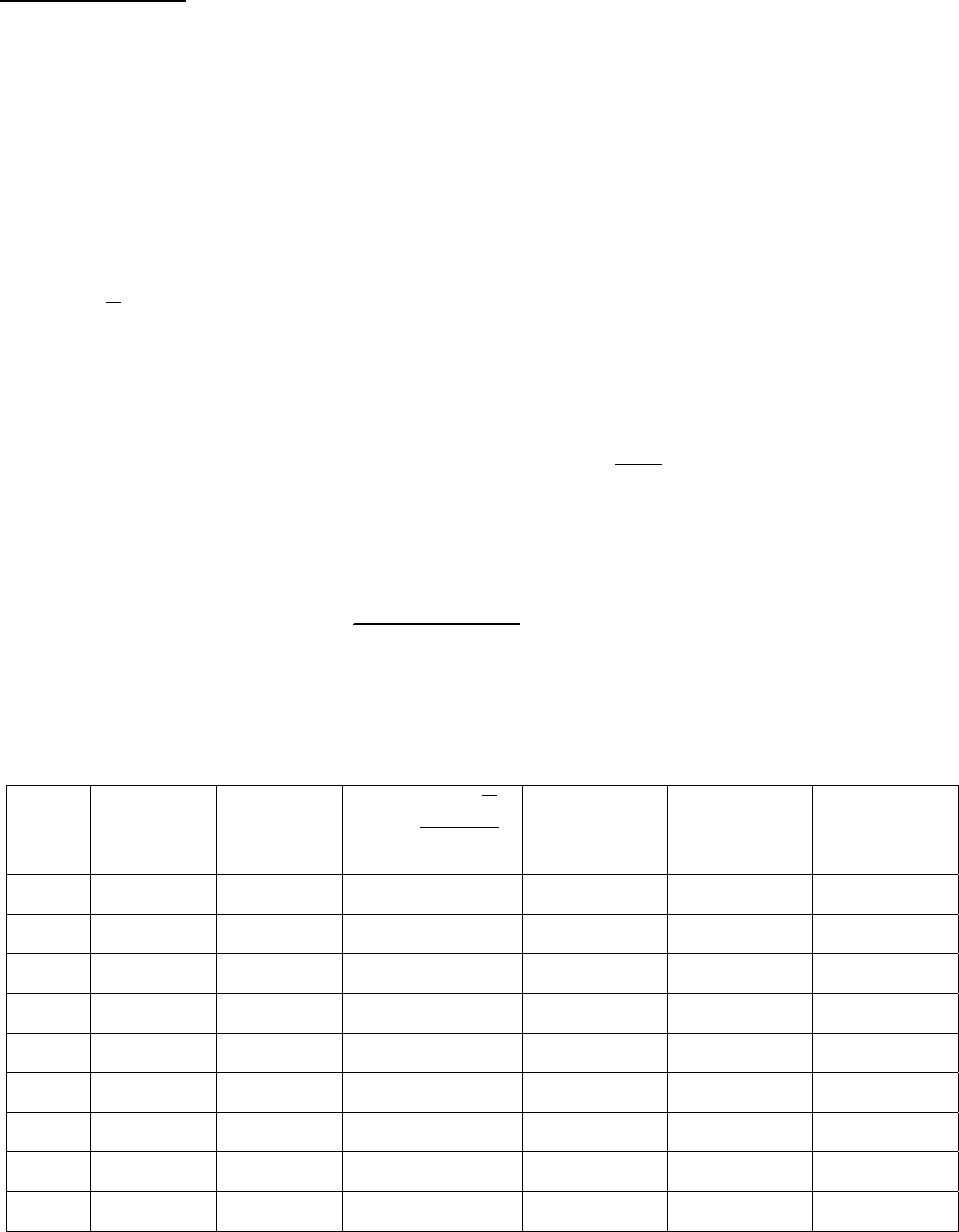
35
П Р И М Е Р 5
(пункт 8 части 1 Задания):
Требуется для выборки (таблица 1) с помощью критерия согласия
Пирсона
2
χ
проверить гипотезу
0
H
о виде распределения генеральной
совокупности (нормальное распределение) на уровне значимости
1,0
=
α
.
Сделать статистический вывод.
Для данной выборки объема
99n
=
ранее были вычислены выборочное
среднее
9961,4=
x
и модифицированная выборочная дисперсия 1332,5
2
0
=S ,
составлен группированный вариационный ряд (таблица 6), а также выдвинута
гипотеза
0
H
о нормальном распределении генеральной совокупности.
Вычислим теперь вероятности
i
p
(
)
Ni ,1=
попадания значений
случайной величины
X в i -тый интервал и выборочное значение статистики
критерия
2
χ
:
2
2
1
()
N
ii
выб
i
i
nnp
np
χ
=
−⋅
=
⋅
∑
.
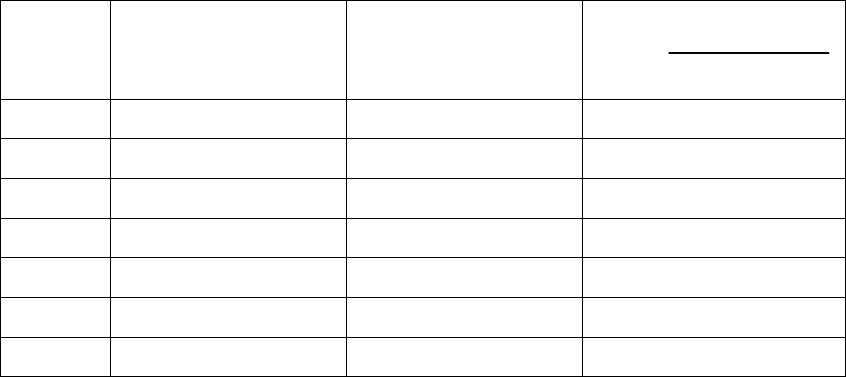
Результаты вычислений занесем в таблицу 10.
Таблица 10
i
i
u
i
n
0
S
xu
t
i
i
−
=
)(
0 i
t
Φ
i
p
i
np
⋅
1 -1,2 -2,7348 -0,4968
2 0,20 2 -2,1169 -0,4830 0,0138 1,3662
3 1,60 3 -1,4989 -0,4332 0,0498 4,9302
4 3,00 18 -0,8810 -0,3106 0,1226 12,1374
5 4,40 20 -0,2631 -0,1026 0,2080 20,5920
6 5,80 24 0,3548 0,1368 0,2394 23,7006
7 7,20 16 0,9728 0,3340 0,1972 19,5228
8 8,60 9 1,5907 0,4441 0,1101 10,8999
9 10,00 7 2,2086 0,4864 0,0423 4,1877
Пятый столбец таблицы 10 можно вычислить с помощью статистической
функции НОРМРАСП пакета EXCEL. Шестой столбец представляет собой
разности значений из пятого столбца:
(
)()
iii
ttp
010
Φ
−
Φ
=
+
.
36
Заметим, что в таблице 9 вычислялись значения функции Лапласа в
серединах интервалов, а в таблице 10 для проверки критерия
2
χ
– именно в
концах интервалов разбиения.
Так как в двух первых и в последнем интервалах не выполняется условие
5
i
np⋅≥
, то объединим эти интервалы с соседними. При объединении
интервалов значения
i
n и
i
np⋅ суммируются (таблица 11).
Таблица 11
i
i
n
i
np
⋅
2
2
()
ii
i
i
nnp
np
χ
−⋅
=
⋅
1
5 6,2964 0,2669
2
18 12,1374 2,8317
3
20 20,5920 0,0170
4
24 23,7006 0,0038
5
16 19,5228 0,6357
6
16 15,0876 0,0552
Сумма 99 3,8103
Суммируя элементы последнего столбца таблицы 11, получим
8103,3
2
=
выб
χ
. Число степеней свободы после укрупнения таблицы 10 равно
31261 =−−=−−=
s
N
q ( 6
=
N
, так как в укрупненной таблице 6
интервалов). Область принятия гипотезы можно записать в виде
()
∫
=−==≤
2
0
2
1)(
кр
pdxxfKP
kкр
χ
αχ
,
откуда следует, что критическое значение
2
кр
χ
совпадает с квантилем
(
)
k
p
2
χ
распределения хи- квадрат с доверительной вероятностью
α
−= 1p .
В нашем случае
1,0=
α
и 9,01
=
−
=
α
p , число степеней свободы
3=q . По таблице П 5 Приложения (или функции ХИ2ОБР) находим значение
критической точки распределения (квантили)
(
)
22
0,9
36,251
кр
χχ
==. Так как

37
[
)
2
3,8103 0 ; 6,251
выб
χ
=∈ , то на данном уровне значимости гипотеза
0
H
принимается.
Статистический вывод: данная выборка согласуется с гипотезой о
нормальном распределении с параметрами
4,9961mx
=
= , 2657,2
0
== S
σ
на уровне значимости
1,0=
α
, то есть вероятность отвергнуть гипотезу
0
H
,
при условии, что она верна, равна
1,0 .
1.9. ИНТЕРВАЛЬНЫЕ ОЦЕНКИ
ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ
Интервальное оценивание параметров распределения генеральной
совокупности состоит в построении доверительных интервалов.
Доверительным интервалом для параметра
θ
называется интервал
()
21
,
θ
θ
, содержащий истинное значение параметра с заданной вероятностью
α
−=1p . Таким образом,
(
)
α
θ
θ
θ
−
=
<
<
1
21
P . Число
α
−
=
1p
называется доверительной вероятностью, а значение
α
– уровнем
значимости.
При построении доверительных интервалов вводят в рассмотрение
специально подобранную статистику
K
, распределение которой известно.
Наиболее распространенными являются статистики, имеющие нормальное,
Стьюдента и
2
χ
распределения.
Методика построения доверительных интервалов для отдельных
параметров распределения генеральной совокупности зависит как от вида
распределения, так и от знания значений остальных параметров закона
распределения.
1.9.1. Рассмотрим задачу построения доверительного интервала для
математического ожидания
m нормально распределенной генеральной
совокупности при неизвестной дисперсии.
38
Пусть случайная величина
X имеет нормальное распределение с
параметрами
m и
σ
. Найдем доверительный интервал для математического
ожидания
m в предположении, что дисперсия
2
σ
неизвестна и задан уровень
значимости
α
.
Английский математик Госсет (псевдоним Стьюдент) доказал, что
статистика
0
xm
Tn
S
−
=
имеет распределение Стьюдента с
1
−
=
n
k
степенями свободы. Так как кривая плотности вероятностей распределения
Стьюдента симметрична относительно
0
=
t
, будем искать доверительную
область в виде:
()
()()
1
k
PT P T f tdt p
τ
τ
τ
ττ α
−
<=−<<= ==−
∫
.
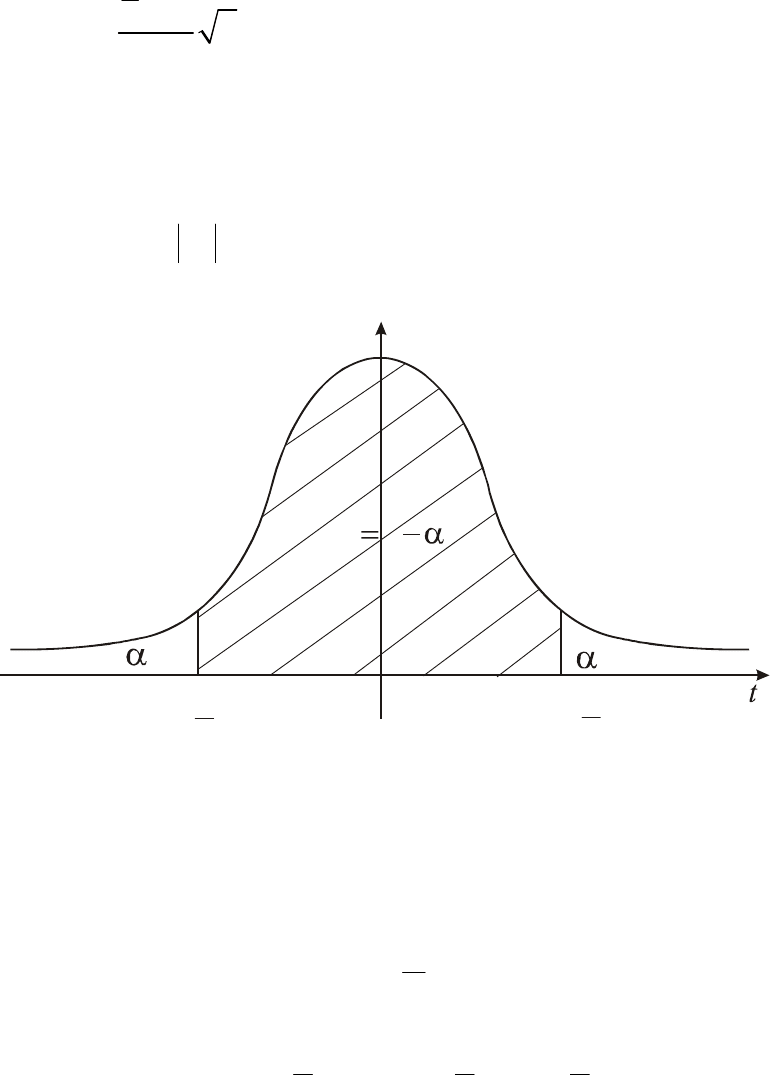
Рис. 11
Геометрическое пояснение смысла квантилей
распределения Стьюдента
Из рисунка 11 видно, что площадь под графиком каждого из
симметричных «хвостов» будет равна
2
α
, тогда значения границ интервала
совпадут с квантилями
1
2
t
α
τ
−
= и
1
22
tt
α
α
τ
−
−
==− .
0
1
p
2
α
t
2
1
α
−
t
)(
tf
k
2/
2/

39
В таблице П 4 Приложения приведены значения
)( kt
p
в зависимости от
доверительной вероятности
p и числа степеней свободы
1−= n
k
. Можно
также использовать функцию СТЬЮДРАСПОБР пакета прикладных программ
EXCEL.
Таким образом, получаем:
2
1
2
αα
−
<
<
tTt
или
11
0
22
xm
tnt
S
α
α
−−
−
−< <
.
Подставив в полученное неравенство значения
1
2
t
α
−
,
x
,
0
S , n и
разрешив это неравенство относительно
m, получим доверительный интервал
для неизвестного математического ожидания
m нормально распределенной
случайной величины
X с неизвестной дисперсией
2
σ
и заданным уровнем
значимости
α
:
00
11
22
SS
xtmxt
nn
α
α
−
−
−⋅ <<+⋅ .
П Р И М Е Р 6
(пункт 9 части 1 Задания):
Требуется построить доверительный интервал для математического
ожидания нормально распределенной генеральной совокупности с параметрами
mx=
и
0
S=
σ
для уровней значимости 1,0
=
α
, 05,0
=
α
и 01,0=
α
при
неизвестной дисперсии.
При построении доверительного интервала для неизвестного
математического ожидания
m нормально распределенной генеральной
совокупности используется статистика
0
xm
Tn
S
−
=
, имеющая распределение
Стьюдента с
1
−
= n
k
степенями свободы. Общее уравнение доверительного
интервала
α
θ
θ
−
=∈ 1));((
21
TP в данном случае имеет вид:
1
0
22
xm
tnt
S
α
α
−
−
<<.

40
Вычислим этот интервал для различных уровней значимости.
1,0=
α
:
05,0
2
=
α
,
95,0
2
1 =−
α
,
981991 =−=−= n
k
– число степеней свободы.
Так как в таблице П 4 Приложения нет числа степеней свободы
98=
k
, то для
вычисления
)( kt
p
можно воспользоваться одним из трех методов.
1. Известно, что при
30≥
k
pp
Ckt
≈
)( , где
p
C – квантиль
нормального распределения (таблица П 3 Приложения). Тогда
0,95 0,95
1
2
(98) (98) 1,645ttC
α
−
=≈=,
0,05 0,95
2
(98) (98) 1,645tt C
α
=≈−=−.
2. Можно использовать линейную интерполяцию между точками таблицы
П 4 Приложения
()( )
671,1;60;
11
=tk и
(
)
(
)
658,1;120;
22
=
tk . Значение
квантили при
98=
k
найдем по формуле линейной интерполяции:
() ()
21
0,95 1 1
21
1,658 1,671
(98) 98 60 1,663
120 60
tt
tkkt
kk
−
−
=⋅−+= ⋅−=
−−
.
Тогда
0,05
2
(98) (98) 1,663tt
α
==−.
3. Статистическая функция СТЬЮДРАСПОБР пакета EXCEL дает
значение квантили
0,95
(98) 1,661t
=
. Нужно иметь в виду, что в EXCEL
вычисляются значения двусторонних «антиквантилей»
()
p
P
Tx p>=.
Поэтому чтобы получить значение односторонней квантили
0,95
(98)t
, нужно
в этой функции задать вероятность
(
)
1,095,012
=
−
⋅
=
p (см. справку к
функции СТЬЮДРАСПОБР).
В дальнейших расчетах используем значения, даваемые EXCEL.
