Dorst L., Fontijne D., Mann S. Geometric Algebra for Computer Science. An Object Oriented Approach to Geometry

Подождите немного. Документ загружается.

462 CONSTRUCTIONS IN EUCLIDEAN GEOMETRY CHAPTER 15

∑

Figure 15.13: Construction of the contour circle K of a dual sphere σ = Σ

∗

seen from a

point p (see Exercise 9).

15.8 PROGRAMMING EXAMPLES AND EXERCISES

The three examples for this chapter are interactive versions of Figure 15.2 (the plunge),

Figure 15.8 (afﬁne combinations of points), and Figure 15.10 (Euclidean projections),

respectively.

15.8.1 THE PLUNGE

This example draws a green circle that is the plunge of the following three primitives:

const int NB_PRIMITIVES = 3;

mv g_primitives[NB_PRIMITIVES] = {

// point:

c3gaPoint( — 1.0f, 1.5f, 0.0f),

// dual sphere:

3.25f * e1 + 2.68f * e2 — 0.34f * e3 + 1.00f * no + 8.43f * ni,

// dual plane:

— e2 + 2.0f * ni,

};

Computing and drawing the plunge is as simple as

draw(g_primitives[0] ^ g_primitives[1] ^ g_primitives[2]);

You can translate the sphere and the point. Notice how the circle always intersects the

point, sphere, and plane orthogonally.

SECTION 15.8 PROGRAMMING EXAMPLES AND EXERCISES 463

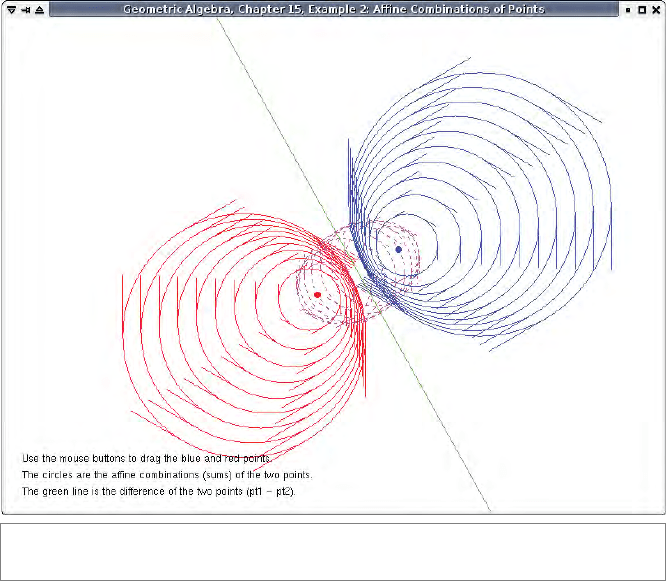
15.8.2 AFFINE COMBINATIONS OF POINTS

As described in Section 15.2.4, afﬁne combinations of points are circles in E

. This

example uses

c2ga to implement an interactive version as shown in Figure 15.14. The

code to draw the circles is:

const mv::Float STEP = 0.1f;

for (mv::Float lambda = — 1.0f; lambda <= 2.0f; lambda += STEP) {

// set color, turn GL stipple on when circle is imaginary.

// ... (omitted)

// draw the circle:

draw(lambda * g_points[0] + (1.0f — lambda) * g_points[1]);

}

As an extra feature, the example also draws the bisecting line (in green) between the two

points, using:

draw(g_points[0] - g_points[1]);

Figure 15.14: Screenshot of Example 2.

464 CONSTRUCTIONS IN EUCLIDEAN GEOMETRY CHAPTER 15

Figure 15.15: Screenshot of Example 3. The green circle is projected onto the blue plane.

The projection is drawn in cyan. The sphere is the

plunge of circle and plane, which explains

the geometry of the projection.

15.8.3 EUCLIDEAN PROJECTIONS

As described in Section 15.3, orthogonal projection in the conformal model behaves

somewhat unexpectedly. This example draws a line or circle, and its projection onto a

plane. You can change the arguments interactively, and optionally cause the

plunge to be

drawn. Figure 15.15 shows a screenshot.

From formula to program is straightforward, for the projection itself is drawn using

// CL is circle or line

// PL is plane

draw((CL << inverse(PL)) << PL);

and the optional plunge is drawn as:

draw(CL ^ dual(PL));

CONFORMAL OPERATORS

Even with all the new techniques for Euclidean geometry in the previous three chapters,

the possibilities of the conformal model are not exhausted. There are more versors in it,

and they represent other useful transformations. Euclidean motions were just a special

case of doing conformal transformations, which preserve angles. These also include reﬂec-

tion in a sphere and uniform scaling.

All conformal transformations are generated by versor products using the elementary

vectors of the conformal model. Whereas the Euclidean motions of the previous chapter

involved using the vectors representing dual planes, we now use the dual spheres. An

important operation we can then put into rotor form is uniform scaling, and that per-

mits a closed-form solution to the interpolation of rigid body motions with scaling.

The fact that the general conformal transformations can be represented as versors ﬁnally

explains the name of the conformal model.

16.1 SPHERICAL INVERSION

The most elementary conformal transformation is the reﬂection in a unit sphere, called

(spherical) inversion. As a versor, the spherical inversion in the unit sphere Σ around the

465

466 CONFORMAL OPERATORS CHAPTER 16

origin involves the vector σ = o −∞/2, representing this sphere dually. The spherical

reﬂection is performed by the versor product:

X → σ



X σ

−1

A unit sphere of weight 1 (so that −∞· σ = 1) is equal to its own inverse, simplifying the

equation slightly. We compute the effect on the basic elements:

o →−(o −

∞) o (o −

∞) = −

∞o ∞ = ∞/2

∞ →−(o −

∞) ∞(o −

∞) = −o ∞o = 2o

E → (o −

∞)



E (o −

∞) = −



E ∞ +

∞



E o = −E(o ·∞) = E.

It is clear that this is not a Euclidean transformation, for ∞ is not preserved but

interchanged with o (and weighted). Geometrically, this is understandable: the point at

inﬁnity reﬂects to the center of the sphere, and vice versa. The total result on a point

x =

[o] is

[o] = o + x +

∞ → x



o + x

−1

−2

∞



= x

−1

[o].

Not only does the point x endupatlocationx

−1

(which is the inverse of x, hence the name

inversion), but its weight also changes by a factor x

. A real dual unit sphere gives a point

in the same direction as x; an imaginary dual unit sphere gives

[o] →−x

−x

−1

[o] (as

you can derive in structural exercise 1). Therefore the latter performs an inversion, while

simultaneously reﬂecting in the origin, which is somewhat surprising but pleasant to have

available as a versor.

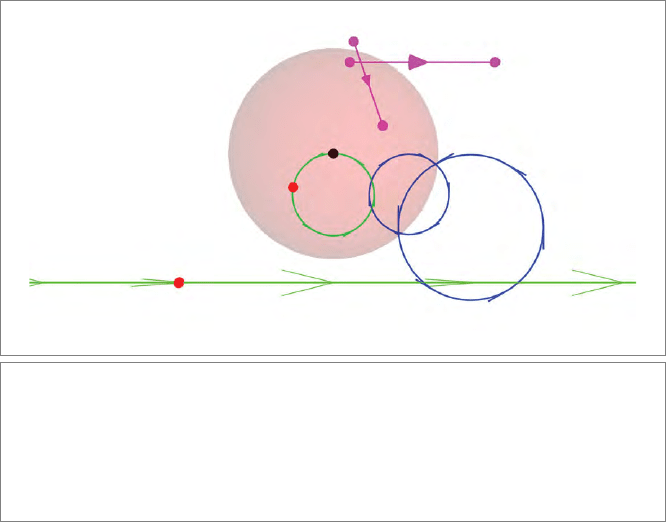
Figure 16.1 shows the inversion of various elements in a sphere. Containment relation-

ships are of course preserved, but there is more. The spherical inversion is a conformal

transformation: it preserves local angles. In the ﬁgure, the angle between the green line

and blue circle is the same as between their images after reﬂection. This angle preserva-

tion property is best demonstrated by considering two tangents at the same location p,

which are p ∧



p(u ∞)



and p ∧



p(v ∞)



. Inverting the tangent p ∧



p(u ∞)



using

the equations above, we ﬁnd it in a nonstandard form as



∧





(u o)



where we used the notation p



for the unit point at location p

−1

. Using the direction

formula from Table 14.1 and some algebraic simpliﬁcation, you can establish that the

direction of this tangent equals −pup∞. Therefore the inversion of the tangent can be

written in standard form as



∧





(−pup∞)



The other tangent transforms in a similar way. If we now study the ratio of their

Euclidean direction vectors at their common location, that transforms from v/u to

SECTION 16.2 SPHERICAL INVERSION 467

σ p σ

−1

∧

σΛσ

−1

∧

σ Γ σ

−1

∧

σKσ

−1

Figure 16.1: Inversion of various elements in a unit sphere (shaded in red) produces their

reﬂection relative to that sphere. We show a point p at location p relative to the sphere’s origin

(denoted in black) that becomes a point at location 1/p; an oriented line Λ that becomes a circle

through the center; a circle K that becomes a circle; and a point pair Γ that becomes a point

pair. The black point at the center is the reﬂection of the point at inﬁnity. Labels of the rounds

are indicated at their centers. All containment and composition relationships are preserved, as

are angles between the elements before and after reﬂection.

(−pvp)/(−pup) = p (v/u) p

−1

. This is a simple reﬂection in the plane with normal

p. For the two vectors u and v, it affects the attitude of their plane u ∧ v, but not the

magnitude of their relative sine or cosine. So although being in a different plane, the

angle between u and v is preserved. It follows that reﬂection in a plane is a conformal

transformation, and so is reﬂection in a sphere.

In contrast to the Euclidean operators we treated so far, the inversion in the sphere does

not preserve the class of the element it acts on: the consequence of essentially swapping o

and ∞ is that ﬂats can become rounds and directions can become tangents at the origin.

This is also clear from the characterization of the classes in Table 14.1, which worked by

testing whether ∞X and/or ∞∧X are zero: the nonpreservation of ∞ implies that such

a condition holding for X may not hold for the transformed X.

Spherical inversions have interesting applications, and a well-chosen inversion can often

transform a geometrical problem into a much simpler problem. Many examples of

this may be found in [46], though in a classical form using complex numbers in the

plane.The conformal model allows a much more powerful treatment of this principle

in n-dimensional base spaces.

468 CONFORMAL OPERATORS CHAPTER 16

16.2 APPLICATIONS OF INVERSION

16.2.1 THE CENTER OF A ROUND

We have seen above how the point at inﬁnity ∞ was reﬂected into (twice) the center o

of the unit sphere at the origin that we were considering. Due to the versor nature, this

result is translation-covariant, so that the center of an arbitrar y sphere can be obtained by

reﬂection of ∞ in it. There are some constants involved to obtain the center in normalized

form, and the resulting formula is

center of sphere: c = −

σ ∞σ

−1

= −

σ ∞σ

(∞·σ)

resulting in a normalized point. A general round can be factored into a sphere cut by

planes through its center. T hose subsequent reﬂections do not disturb the location of the

center, so the general formula is as indicated in Table 14.1.

16.2.2 REFLECTION IN SPHERES AND CIRCLES

The straightforward application of spherical inversion is to compute the reﬂection in a

sphere of arbitrary elements. We have used this above in Figure 16.1 for the reﬂection

in a unit sphere around the origin. By now you should be conﬁdent that this may be

extended to arbitrar y spheres anywhere, because it is a versor product, and will therefore

combine well with other versor products. We can move the unit sphere or the elements

anywhere, in any orientation, and still σ



X /σ will perform the reﬂection, as illustrated in

Figure 16.2. The only thing we cannot show now is that we are also allowed to change

the radius of the sphere in a structure-preserving manner, although this may be obvious

geometrically. We leave that until after we have the rotor for that scaling (already in the next

section), and that will permit the rotor representation of reﬂection in spheres of arbitrary

radius.

We can also compose the reﬂections, ﬁrst reﬂecting in a plane π and then in a sphere σ

cutting the plane orthogonally (so that π ·σ = 0). The total result is that we have used the

versor πσ:

reﬂection in a circle: X → (πσ)



X (πσ)

−1

Since π was chosen through the center of the sphere σ, the versor πσ is the dual repre-

sentation of the circle that is their meet (as in the factorization of Section 15.2.3). This

versor construction therefore gives a sensible meaning to reﬂection in a circle. In its plane,

this acts like spherical inversion, but it can also be extended to act outside that plane.

We found it hard to draw a convincing picture of this; because of its essential 3-D nature,

it is best studied live in an interactive visualization. Structural exercise 3 explores reﬂection

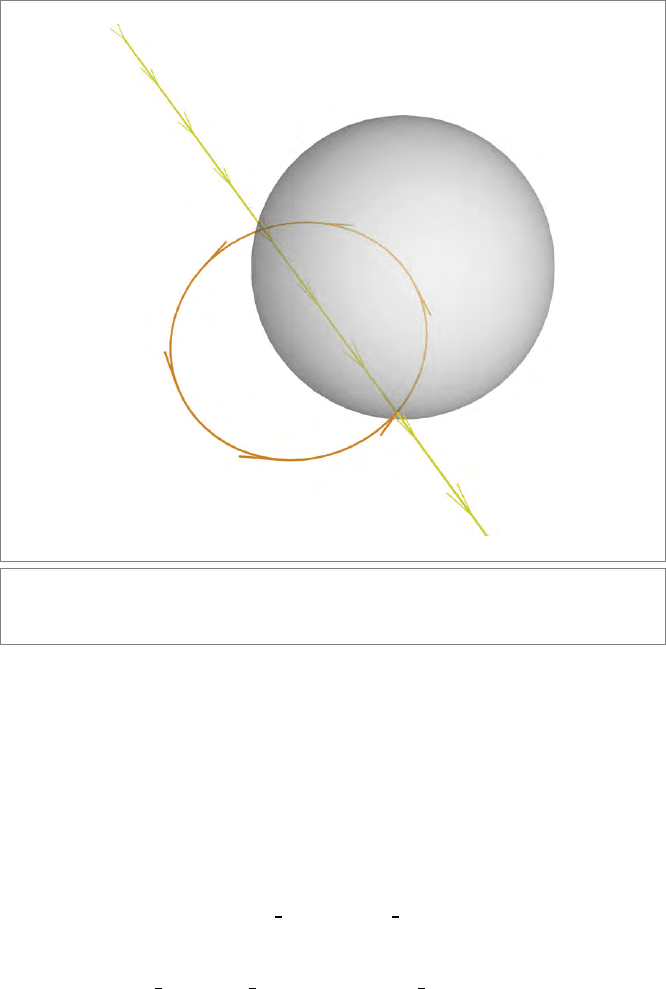
SECTION 16.3 SCALING 469

∧

σΛ/σ

Figure 16.2: An oriented Euclidean line Λ is reﬂected in a sphere σ by the versor product



−1

to become a circle through the center.

in a point pair, which is interestingly different from spherical reﬂection, even in the

plane.

16.3 SCALING

16.3.1 THE POSITIVE SCALING ROTOR

In Section 13.2.2, we generated a translation from reﬂections in two parallel dual planes.

The natural question now is: What can we generate from the reﬂections in two “parallel”

spheres (i.e., concentric spheres o −

∞ and o −

∞)?

We obtain a composite versor that is the product of the two inversions, and simplify:

(o −

∞)(o −

∞) = (ρ

+ ρ

) −

(ρ

− ρ

) o ∧∞.

470 CONFORMAL OPERATORS CHAPTER 16

One would expect only the ratio of the sizes of the spheres to matter. We rescale the versor

through dividing by 2ρ

, and conveniently deﬁne a characteristic parameter γ through

exp(γ/2) = ρ

/ρ

Now some algebraic manipulation gives a pleasant standard form,

= cosh(γ/2) + sinh(γ/2) o ∧∞= e

γ o∧∞/2

where the rewriting of the resulting rotor as an exponential uses the results in Section 7.4

combined with (o ∧∞)

= 1.

You may guess what the effect of this rotor is, since you know that it is geometrically a dou-

ble sphere inversion: it scales elements relative to the origin. We compute what happens to

the basic components of our representation. For brevity deﬁne O ≡ o ∧∞(it represents

the unit ﬂat point at the origin), and note that O

= 1,aswellasOo = −o = −oOand

O ∞ = ∞ = −∞O. With that, it is easy to derive that

[∞] =



cosh(γ/2) + sinh(γ/2) O



∞



cosh(γ/2) − sinh(γ/2) O





cosh(γ/2) + sinh(γ/2) O



∞ = e

∞.

Using the commutation relationships, you should dare to abbreviate this derivation as

[∞] = e

γO/2

∞e

−γO/2

= e

γO

∞ =



cosh(γ) + sinh(γ) O



∞ = e

∞.

(16.1)

(Verify all steps in detail, if you need to be convinced.) Similarly,

[o] = e

γO/2

−γO/2

= e

γO

o =



cosh(γ) − sinh(γ) O



o = e

−γ

(16.2)

The bivector O commutes with a purely Euclidean blade x,so

[E] = E.

In total, we ﬁnd for the transform of a general point x =

[o]

[x] = e

−γ



o + (e

x) +

∞



= e

−γ

[o]. (16.3)

This clearly shows that the spatial aspects are scaled by e

(as well as weighted by e

−γ

So this is indeed a spatial scaling. You should realize that it has been characterized by an

exponential parameter; so to obtain a scaling by a factor of 2, you need to use γ = log(2).

Note that this transformation is almost a Euclidean transformation: it does not quite pre-

serve the point at inﬁnity (as a Euclidean transfor mation would), but it merely weights it

(which is not too bad). In particular, the ty pe of an element is preserved in scaling, since

the conditions of Table 14.1 are not affected by a weight on ∞. So rounds remain rounds,

SECTION 16.3 SCALING 471

and ﬂats remain ﬂats. No Euclidean transformation can affect the size of an object, but

once it has been determined by a scaling, it is nicely preserved.

There is a slight paradox in this use of the scaling rotor. The distance between Euclidean

point representatives was originally deﬁned through a ratio of inner products by (13.2). If

the distance between the points should increase, so should the value of that inner product

ratio. But the inner product is an invariant of the orthogonal transformation produced

by the scaling rotor (by deﬁnition of an orthogonal transformation). When you check,

you ﬁnd that this indeed holds, because the scaling changes ∞ to e

∞ and (16.3) trades

spatial scale for point weight.

However, if we use the distance deﬁnition relative to the original point at inﬁnity ∞,we

ﬁnd that the Euclidean distance of the points has indeed increased by a factor of e

after

scaling by S

. Apparently, that is how we should use the deﬁnition of distance: always

relative to the original point at inﬁnity.

This inter pretation afterwards of course does not affect the consistency of the conformal

model computations. Having scaling available as a rotor means that all our constructions

are automatically structurally preserved under a change of scale—we never need to check

that they are. For instance, any construction made with a unit sphere using the products

of our geometry can be simply rescaled to involve any sphere of any radius at any position

without affecting its structure. This scaling does not even need to be done relative to the

origin; by virtue of the structure preservation, a scaling around another location t is simply

made by applying the translation rotor to the scaling rotor to obtain the translated scaling

16.3.2 REFLECTION IN THE ORIGIN: NEGATIVE SCALING

When one of the parallel two reﬂecting spheres is imaginary, their product is a versor that

is capable of reﬂecting in the origin. The prototypical example of this is the product of

two unit spheres, one real, one imaginary. This gives the element

(o −∞/2) (o + ∞/2) = o ∧∞.

This is the ﬂat point in the origin, which makes perfect sense: negative scaling is like reﬂec-

tion in the origin. Its action on a conformal point is

[o] →−T

−x

[o].

Even though this is an even versor, it is not a rotor, for (o ∧∞)(o ∧∞)= −1. Therefore

it cannot be performed in small amounts, and it cannot be expressed as the exponential

of a bivector. It is a transformation, but not a motion.

You can combine this reﬂection in the origin with a scaling versor to effectively make a

versor that can perform a negative scaling.