Dorst L., Fontijne D., Mann S. Geometric Algebra for Computer Science. An Object Oriented Approach to Geometry

Подождите немного. Документ загружается.

452 CONSTRUCTIONS IN EUCLIDEAN GEOMETRY CHAPTER 15

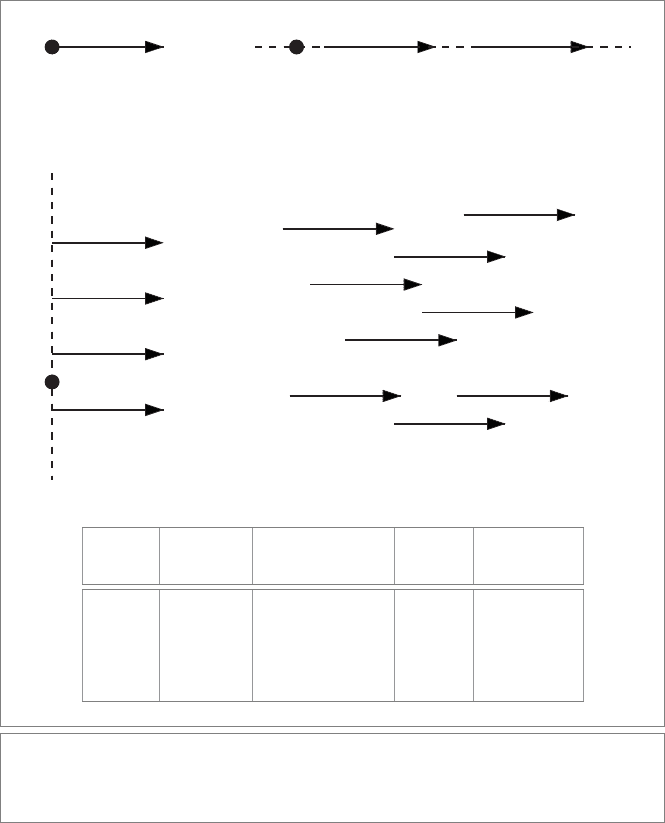
Line vector

Free vector

Normal vector

Tangent vector

Ve c t or Origin Translated Squared Localization

Type Form Form Norm Symmetry

Free u ∧∞ u ∧∞ 0 space

Normal u p(u ∧∞) u

plane

Line o ∧ u ∧∞ p ∧ u ∧∞ −u

line

Tangent o ∧ u p ∧ ( p(u ∧∞)) 0 point

Figure 15.11: In the conformal model, the various kinds of vectorlike concepts of Euclidean

geometry are clearly distinguished, each with its own form properly transforming under the

permissible Euclidean transformations.

so that it is translation-invariant. It has no speciﬁc location, so this is truly a free

vector. It corresponds to the entity u in the homogeneous model. In the conformal

model, it is the parameter of the translation rotor exp(−u ∧∞/2). That rotor can be

applied anywhere, and we now see why we are allowed to draw its action as a vector

at any location, as is customary.

SECTION 15.4 APPLICATION: ALL KINDS OF VECTORS 453

•

Normal Vector u. The normal vector of a plane in the origin is the purely Euclidean

element u, just as in the vector space model. It clearly indicates a direction vector, for

applying a rotation to it we get

R[u]. However, there is also a translational element.

Applying the translation rotor gives

[u] = p(u ∧∞) = u + (p · u) ∞.

There are two consequences of this equation. First, it shows that the element u is

insensitive to translations in the directions perpendicular to u. We can depict it

freely anywhere in the dual plane u. It therefore truly is a normal vector of the

plane; the classical liberty to draw such a normal vector anywhere on the plane is

now fully part of the internal algebraic freedom of the computational element.

The second consequence is that this equation gives the normal vector representa-

tion of a plane with normal direction u passing through p instead of o.Itisonlythe

component p · u that affects the representation, and we recognize that as propor-

tional to the oriented distance to the origin. This is the correct 1-D locational aspect

of the plane: only its u-component matters.

•

Line Vector o ∧ u ∧∞. A concept that is less explicit in classical considerations

in geometry is the direction vector of a line. It is important in classical mechanics,

where it is used to denote a force. Such a force is free to act anywhere along its carrier

line, and therefore is a vector-like concept that should be permitted to slide along a

well-deﬁned line.

An element with the correct symmetry is o ∧ u ∧∞, which we are used to viewing

as the line itself. It rotates to o ∧ R[u] ∧∞, which clearly indicates that it has a 1-D

directional aspect. When we translate it, we obtain

[o ∧ u ∧∞] = p ∧ u ∧∞= o ∧ u ∧∞+ (p ∧ u) ∧∞.

Again there are two consequences of this equation. First, it shows that the element

is invariant under translations for which p ∧ u = 0 (i.e., motions along the line).

Second, it shows how to make a general element with this property, passing through

the point p. Only the part of p perpendicular to u affects the location, so a line in 3-D

has a 2-D locational parameter complementary (i.e., dual) to its direction vector.

This is effectively the “moment” we encountered in the homogeneous model.

It is perhaps surprising that a line vector should be a 3-blade, but it really unites three

separate concepts: a location p, a direction u, and the straightness in its extension

to the point at inﬁnity ∞. All are required to deﬁne all aspects of its symmetry; the

inclusion of ∞ allows the invariant shifting along the carrier.

•

Tangent Vector o ∧u. A vector with direction u at the point location o is represented

as o ∧ u. A rotation changes this to o ∧ R[u], so that u is its only rotational aspect.

A translation carries the direction vector along with the point. This is perhaps best

seen when we ﬁrst rewrite to o ∧ u = o ∧



o(u ∧∞)



, and then translate:

[o ∧ u] = T

[o ∧



o(u ∧∞)



] = p ∧



p(u ∧∞)



454 CONSTRUCTIONS IN EUCLIDEAN GEOMETRY CHAPTER 15

The location p is explicitly present in the result; so the tangent vector has all the

locational aspects of p, and moves with the point it is attached to.

In classical applications, you draw tangent vectors all the time, as velocities, direc-

tions of motions on a surface, and so on. Apparently we can do a lot without having

them explicitly represented as an element of computation—but now that we have

this representation, we can use it. We will see several examples of its potential use

in the ray tracer application of Chapter 23.

•

Position Vector. The most common informal use of a Euclidean vector u has no

counterpart in the conformal model: to denote a point in space. That practice

attempts to use an element of the vector space model (the algebra of directions)

to denote a location. This is only possible by using some standard point, namely an

origin o, as a reference. We need to make this algebraically explicit: if u is meant to

emanate from o, the position vector should encode o in its deﬁnition. That makes

it either the tangent vector o ∧ u or the line o ∧ u ∧∞. It is not the line, for

that loses essential aspects of the location o due to its linear translation symmetry.

The position vector has some feature of the tangent vector o ∧ u, and can be seen

as an amount of travel along that vector. But that encodes one point (p)intermsof

another (o), and therefore does not really resolve the issue.

Of course, in the conformal model we have a much better alternative: the point

is represented as the representational null vector u. If we should want to know its

location relative to any other point q, that is the Euclidean vector u − q = u − q +

(u · q) ∞, but you do not need to know that to compute with the point u.

The representative vector for the point u may be obtained by using u in a translation

rotor applied to q. Taking q = o, that gives us the correspondence to the classical

characterization by a relative position vector:

u =

u−o

[o] = e

−u∞/2

u∞/2

There is now a clear distinction between the vector parameter u characterizing the

location and the standard element o to which it is to be applied. If o is chosen dif-

ferently, u needs to change to reach the same point u. There is of course nothing

geometrically intrinsic about the position vector u ofapointu, and it is no wonder

that the many tacit conventions in this position vector representation of a point are

a source of errors and abuse. Homogeneous coordinates were the ﬁrst step to a true

point representation, but only the conformal model gives the full operational func-

tionality expected from the representation of the most basic elements of geometry.

So, in summary: there is no need for separate data structures for the various kinds of

vectors. As basic elements of computation, they are an integral element of the algebra,

automatically inheriting their relationships with other elements through all of its prod-

ucts. Using this operational model of Euclidean geometry gives us more precision and

ﬂexibility, and simpler code. There is a small computational overhead to this, which we

SECTION 15.5 APPLICATION: ANALYSIS OF A VORONOI CELL 455

discuss in Part III; in a good implementation, this can be kept below 25 percent (which is

actually also the cost of employing the structurally inferior homogeneous coordinates).

Paradoxically, such efﬁciency is achieved by recognizing the class of an element and treat-

ing it with dedicated code; but the difference with the classical approach is that this special

code is established by an automatic code generator rather than by the programmer herself.

15.5 APPLICATION: ANALYSIS OF A VORONOI CELL

To give an example of how the conformal model can be used in derivations of expres-

sions, we take a detailed example from planar geometry involving distances in an essential

manner. Given four points p, q, r, s in the plane, we will compute the potential edge of the

Voronoi diagram across the common edge pr of the triangles prs and pqr. We compute all

its parameters, its carrier line, an end point, and its edge length. In the classical approach,

this would involve a lot of trigonometry, which in turn would require you to deﬁne a host

of intermediate variables and edge length parameters, as in Figure 15.12(b). We will show

how it can all be done based on the four points only, with seemingly no trigonometry at

all. You should see this as an isolated exercise in uncovering some common computational

techniques for this type of problem.

We will go slowly and point out useful techniques on the way. You can skip this section

without missing much, though you may want to contrast the directness of the conformal

model result (15.8) (fully expressible in the original four points) with the classical result

(15.10) (which requires many derived quantities even to be stated).

15.5.1 EDGE LINES

To keep life simple, we start from normalized points p, q, r, s, so that −∞ · p = 1, and

so on.

The Voronoi edge element that interests us lies on the perpendicular bisector of the

connection line of p and q, indicated in Figure 15.12(a). A point x on it therefore

satisﬁes x · p = x · q, which we can rewrite to x · (q − p) = 0. Therefore the perpen-

dicular bisector is dually characterized by

dual perpendiculat bisector: q − p.

This element q −p has a weight, a condition number that determines its signiﬁcance. We

can compute the norm squared as

(q − p) · (q − p)

∼

= −2p · q = d

(p, q )

so the norm equals the squared length of the edge connecting p and q. But this poses

the problem of whether to take the positive or negative square root, and thus threatens

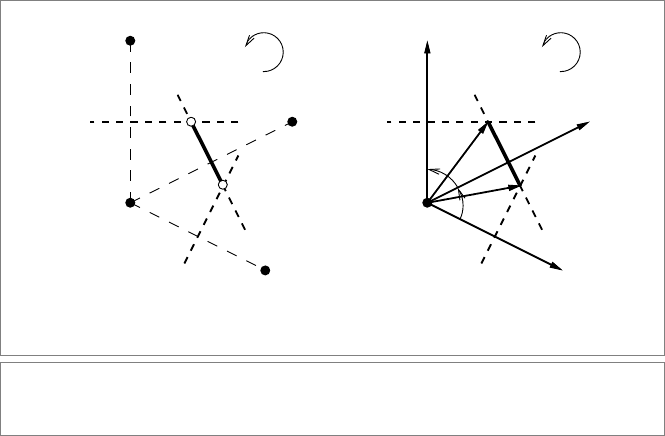
456 CONSTRUCTIONS IN EUCLIDEAN GEOMETRY CHAPTER 15

q − p

(b)

(a)

r − p

s − p

Figure 15.12: Deﬁnition of symbols for the Voronoi derivations, (a) for the conformal model

derivation, and (b) for the classical, p-centered derivation.

to lose valuable orientation information. It is better to retain the directionality by

computing the linear quantity

∞(q − p)

∗



∞∧(q − p)



∗



∞∧(q − p)





o ∧ I

−1

∧∞



= (q − p)

夹

∧∞,

in which ()

夹

denotes the Euclidean dual in the plane. This direction is orthogonal in a

consistent directed manner to the direction vector connecting p to q, so this immediately

gives both length and orientation. Consistency is obtained by relating all such signs and

orientations to the same pseudoscalar of the plane (as implicit in the duality).

15.5.2 EDGE POINT

We form the dual midplane r − q, and compute the intersection of this with the earlier

dual midplane q − p to obtain a ﬂat end point of our edge. This is, dually,

(q − p) ∧ (r − q) = p ∧ q + q ∧ r + r ∧ p,

which incidentally shows in its symmetry that only the order of p, q, r matters, and then

only by changing the sign of the result. We would have obtained the same intersection

by intersecting with the midplane p − r. You can conﬁrm that the result is a dual ﬂat by

taking a contraction with ∞; that indeed gives zero.

This dual ﬂat point is not normalized. (Note that a ﬂat point x ∧∞is normalized when

its norm is 1, and a point x is normalized when its weight is 1 (so that −∞x = 1).) Its

SECTION 15.5 APPLICATION: ANALYSIS OF A VORONOI CELL 457

normalization factor may be useful in further computations of quantitative properties. If

desired, we can normalize a ﬂat point by the algebraic construction

X →

(o ∧∞)X

and this implies that a dual ﬂat point is normalized by the substitution

∗

→

∗

o ∧∞∧X

∗

We can take any point instead of the arbitrary origin o, and it is important to wield this

capability to keep formulas simple. For the dual ﬂat point we just computed, which is

based on a q-centered computation, it seems indicated to take q for the arbitrary origin

point o in the normalization (but we could take r or p as well). That yields as normalized

ﬂat intersection point the circumcenter of the triangle formed by p, q, r:

ﬂat circumcenter: M =

p ∧ q + q ∧ r + r ∧ p

p ∧ q ∧ r ∧∞

15.5.3 EDGE LENGTH

We can compute the other intersection in the quadrangle between the dual midlines (r−p)

and (s − p) in the same manner, and normalize the resulting dual intersection point N

∗

by (p ∧ r ∧ s ∧∞) . From those two intersection points, we should be able to deduce the

length of the potential edge of the Voronoi diagram.

It is possible to do this by computing their square distance, but this again gives

consistency issues in choosing the square root. Let us instead derive this length as

the weight of the line connecting the two intersection points. If we had been in the

homogeneous model, this line would have been M ∧ N. Computations with ﬂats in

the conformal model do not work quite so simply. When we have the ﬂat points

M = m ∧∞and N = n ∧∞rather than the corresponding points m and n,we

compute the desired line m ∧n ∧∞as m ∧N. To do so, we should retrieve m from the

dual ﬂat point M

∗

as oM = (o ∧ M

∗

)

−∗

. This also produces a term proportional to

∞, but the outer product in the line computation kills that anyway, which is a trick

to remember! And again, since we can choose any normalized point as o, we pick q

when we observe that doing so reduces the number of terms in the computation.

We now spell out the manipulation to obtain the connecting line; note that all we really

do is substitution of known properties, perhaps guided by the idea that the result should

be part of the dual line (r − p). We denote the scalar normalizations of the two points by

and α

, to unclutter the formulas.

m ∧ n ∧∞= α



q ∧ (q − p) ∧ (r − q)



−∗

∧



(s − r) ∧ (p − s)



−∗

458 CONSTRUCTIONS IN EUCLIDEAN GEOMETRY CHAPTER 15

= −α



(r − p) ∧ p ∧ q)



−∗

∧



(r − p) ∧ (p − s)



−∗

= −α



(r − p) ∧ p ∧ q)



∗

∧



(r − p) ∧ (p − s)



∗

= −α



(r − p) ∧ (p − s)



∩



(r − p) ∧ p ∧ q



∗

= −α

(r − p)

∗



(r − p) ∧ (p − s) ∧ p ∧ q



∗

= α

(r − p)

∗

(p ∧ q ∧ r ∧ s)

∗

(r − p)

∗

(p ∧ q ∧ r ∧ s)

∗

(p ∧ q ∧ r ∧∞)

∗

(p ∧ r ∧ s ∧∞)

∗

. (15.8)

In the derivation we were striving towards a form that could use the

meet identity (5.11).

The ﬁnal results conﬁrms that we are on the line (r − p)

∗

, and it gives the length of the

resulting segment between M and N. Don’t forget that (r − p)

∗

contributes a factor d

(r,p)

to the length, as we derived above.

Taking q as variable for the moment, the length of the edge segment becomes zero when

p∧q∧r∧s = 0, and this is when q lies on the circle p∧r∧s. Move it beyond the circle and it

changes sign. Negative edge length is an indication that another edge should become the

Voronoi edge, namely the part of (s − q)

∗

computed completely analogously (most simply

by a cyclic permutation of p, q, r, s). It is rather satisfying that this condition is completely

embedded in the basic computation; nowhere did we put in the circle p ∧ r ∧ s explicitly,

but the rearrangements of the outer products just made it appear naturally. The two terms

in the denominator are dual oriented planes describing the two triangles involved; each

term is twice the signed area of its corresponding triangle.

15.5.4 CONVERSION TO CLASSICAL FORMULAS

The above computation using the conformal model was a fairly straightforward applica-

tion of algebra on the combination of the basic points by standard operations. Where it

may not have seemed straightforward, it was because this is the ﬁrst time we encounter

these techniques. The coordinate-free form of the ﬁnal result is rather pleasing, and

directly interpretable in terms of relative point positions.

By contrast, let us show how the results would look in classical form, to show that the

conformal model result conveniently hides a lot of trigonometry. This requires the intro-

duction of lots of symbols for local edge lengths and angles. For that, at least, we can use

the natural correspondence to the geometric algebra of 2-D Euclidean space.

For the following computations, it is convenient to choose the (arbitrary) origin at p,

denoting the Euclidean vectors to q, r, s by q, r, s, respectively. Then the dual plane is

r − p = r +

∞

We will also use polar coordinates relative to p to convert the conformal expressions to

more classical forms. That essentially means that we are using a vector space model based

in p. We deﬁne the norms of q, r, s as κ, ρ, σ, and the angles through the implicit deﬁnitions

also used in the vector space model treatment of a triangle (in (10.3)):

SECTION 15.5 APPLICATION: ANALYSIS OF A VORONOI CELL 459

s/r = σ/ρ e

, r/q = ρ/κ e

␾

so that ψ is the angle from s to r, and ␾ from r to q (see Figure 15.12(b)).

We prefer to redo parts of the computation rather than to perform an immediate

substitution in the ﬁnal conformal result (15.8). This shows the representation of inter-

mediate quantities in an educational manner.

(q − p) ∧ (r − q) = (q − p) ∧ (r − p)

= (q +

∞) ∧ (r +

∞)

= q ∧ r + ∞∧(rq

− qr

)/2

= (1 −

− qr

2 q ∧ r

∞)(q ∧ r).

The ﬁnal form can be interpreted using Table 14.1, or by realizing that it should be the

dual of a ﬂat point x ∧∞, and computing quickly what form such a dual should have:

(x ∧∞)(o ∧



∧∞) = ((o + x) ∧∞)(o ∧



∧∞) =



+ ∞x



= (1 − x ∞)



Either way, it follows that the intersection point is located at

m =

− qr

2q ∧ r

q − κ

2 sin ␾



(15.9)

where

r are unit vectors along q and r, respectively. The intersection has a numerical

strength measured by the norm of q∧r,whichisκρ sin ␾. Incidentally, this is the equation

for the center of the circumcircle of the triangle PQRin its classical form.

The edge length computed before can be converted into a more classical form using the

same polar coordinates relative to p (which is the chosen origin o):

(r − p)

∗

(p ∧ q ∧ r ∧ s)

∗

(p ∧ q ∧ r ∧∞)

∗

(p ∧ r ∧ s ∧∞)

∗

= (r +

∞)

∗



o ∧ (q +

∞) ∧ (r +

∞) ∧ (s +

∞)



∗

(o ∧ q ∧ r ∧∞)

∗

(o ∧ r ∧ s ∧∞)

∗

= (r +

∞)

∗

(o ∧

(κ

r ∧ s + ρ

s ∧ q + σ

q ∧ r) ∧∞)

∗

(o ∧ q ∧ r ∧∞)

∗

(o ∧ r ∧ s ∧∞)

∗

= (r +

∞)

∗

κρσ (−κ sin ψ + ρ sin(␾ + ψ) − σ sin ␾)

2(−κρ sin ψ)(−ρσ sin ␾)

= (

r +

ρ ∞)

∗

−κ sin ψ + ρ sin(␾ + ψ) − σ sin ␾

2 sin ␾ sin ψ

So this gives the length of the edge in completely classical terms as

−κ sin ψ + ρ sin(␾ + ψ) − σ sin(␾)

2 sin ␾ sin ψ

, (15.10)

460 CONSTRUCTIONS IN EUCLIDEAN GEOMETRY CHAPTER 15

and moreover that it is a part of the line orthogonal to

r, passing midway through it (since

the distance to p is clearly

ρ).

The derivation spelled out in this manner may look rather intimidating. Yet it is fully

algebraic from the conformal model result, which itself was straightforward algebra (with

a clear geometrical interpretation). There was no need for the usual careful checking of

signs and symbols with messy ﬁgures to develop the result. And of course, one doesn’t

need to compute this result at all, because the original conformal expression of (15.8) has

the same value. It is a disadvantage of the classical expression that the symmetry is hidden

in the peculiar variables, and that the circumcircle as the essential curve for the change of

sign is hidden in the ﬁnal expression. All one should need to specify for a Voronoi edge are

the original four points, and it is satisfying to see that the conformal model can express

the total quantitative result in terms of those points only.

15.6 FURTHER READING

Geometry using meet and plunge was developed in a 1941 book by Forder [22], which is

full to the brim with useful geometrical results. He uses Grassmann’s notation, in which

a ∧ b is denoted as [ab], and dualization is denoted by |a rather than a

∗

Forder’s book is one of several instances that demonstrate how far Grassmann’s heritage

was developed into quantitative geometry. He wrote it to “redress the balance” between

the use of Grassmann algebra in physics (where he says “it has at last won an established

place”) and in geometry (where it is “less widely appreciated”).

The book may look rather intimidating, but with interactive software should now have

become quite readable: all equations can be drawn, for this is the algebra of geometry.

15.7 EXERCISES

15.7.1 DRILLS

1. Compute the tangent at the origin of the sphere Σ through the points at locations

0, e

, e

, and e

(you computed this sphere Σ in the drills of Chapter 14).

2. Factorize the circle K through the points at locations e

, e

, and e

(you computed

this circle K in the drills of Chapter 14).

3. Use that factorization of the circle K to spot its squared radius, center, carrier, and

surround, by inspection.

4. Project the point at the origin onto the carrier plane of the circle K.

5. Make the free vector, tangent vector, line vector, and normal vector in the direction

, at the origin (if a location is required).

6. Rotate each of the vectors of the previous exercise by π/2 in the e

∧e

plane. Explain

the results.

7. Translate each of the vectors of the previous exercise by e

+ e

. Explain the results.

SECTION 15.7 EXERCISES 461

15.7.2 STRUCTURAL EXERCISES

1. Express the scalar product of two blades in terms of the scalar product of their duals.

It should only differ by a sign, which you should express in terms of the grade of

the blades and the space they reside in.

2. What is the geometry of the element p ∧ u,wherep is a point and u a Euclidean

vector? (Hint: View it as a

plunge. Counterhint: It is not the tangent vector o ∧ u

moved to p.)

3. Show that the tangent of a tangent is zero. (Hint: Realize that a tangent is also a

round; now use (15.1).)

4. On a circle K, ﬁnd the closest and furthest points to a given point c (in n-D!).

Hint 1: Set up a dual sphere with parametric radius around c, and compute the

meet with K. Hint 2: The meet of parametric sphere and K should be a tangent

vector at the desired points. Hint 3: Use the algebraic property of tangents, which

is that they are rounds that square to zero, to get a second-order equation for the

radius, and solve. Hint 4: Compute the locations of the tangent vectors.

5. Show that the dual sphere s = r(p ∧ q) = (rp) q − (rq) p isamemberofthe

parameterized family (15.6), passing through r (but nonnormalized).

6. It is interesting to study the outcome of the construction p(q∧r), which crops

up frequently in some form or other in computations. Depending on whether

you let p, q, r be equal to points, dual spheres, or the point at inﬁnity ∞,

different constructions appear. Play with this construction, either by hand or

(preferably) in an interactive visualization package. What is ∞(q∧r)? What is

r(q ∧∞)?

7. Give the formula for the circle through a point pair p∧q intersecting the dual plane

π perpendicularly, and for the circle having a tangent vector in direction u at p and

plunging into π.

8. Derive the factorization of a dual round (15.5) from the factorization of a direct

round (15.4).

9. Construct the contour of a sphere Σ as seen from a point p (i.e., the circle K of points

where the invisible part of the sphere borders the visible part, as in Figure 15.13).

(Hint: The white sphere in the ﬁgure is a clue to the construction. Express it ﬁrst,

using the

plunge. Then construct the circle as a meet.)

10. You can derive all types of vectors of Section 15.4 by relating them to two

points a and b, which are combined using the various products of geometric

algebra. Identify the types of the following elements and relate them geomet-

rically to a and b: ∞(a ∧ b), ∞∧(a ∧ b), ∞∧(∞(a ∧ b)), ∞(∞∧(a ∧ b)),

a(∞∧(a ∧ b)), a ∧ (∞(a ∧ b)). How is their squared norm related to the

oriented distance of a and b? For the null elements, can you retrieve this

distance in another manner?

11. Show that the tangent with direction element E at p can be written in two equivalent

forms:

tangent E at p: p ∧



− p(



E∞)



= p(p ∧



E ∧∞).