Елизаров А.М. Математические методы в библиотечной работе

Подождите немного. Документ загружается.

мерованы); R

— отношение древесного порядка („де-

рево зависимостей"), устанавливающее систему смыс-

ловых связей между словами в предложении. Для

решения любых информационных задач необходимым

и достаточным является представление предложения

в виде модели (M, R

). С другой стороны, между

двумя видами упорядочения текста — линейным поряд-

ком R

и древесным R

—имеется определенная связь.

Например, для данной последовательности слов одни

деревья зависимости возможны, а другие нет, задан-

ный смысл может быть реализован другим деревом.

Рассмотрим

Пример 6. (Проективность предложения). Даны

слова: описание (2), новой (3), библиографическое (1),

книги (4). Предложение „библиографическое описание

новой книги" имеет вполне определенный смысл,

который наиболее естественно выражается последо-

вательностью слов 1—2—3—4. Смысловые связи между

словами данного предложения могут быть изображе-

ны схематически так:

описание

библиографическое книги

новой

(стрелка над словом „описание" выделяет главное

слово). Указанный смысл (хотя и менее естественно)

выражается следующими последовательностями слов

4—3—1—2, 3—4—2—1, и явно недопустимы доследо-

вателыюсти типа 1—3—2—4, 3—2—4—1, 3—2-1- 4.

Возникает вопрос, как определить разницу между

правильным и неправильным порядком слов. Если

использовать приведенную выше схему зависимостей,

можно прийти к следующему выводу; неправильные

конструкции отличаются от правильных тем, что

стрелки зависимостей в них пересекают друг друга,

либо стрелку-указатель главного слова.

Построим деревья зависимостей предложения та-

ким образом, чтобы вершины его были расположены

в горизонтальном направлении в линейном порядке R

а по вертикали каждое управляемое слово отстояло

от управляющего слова точно на один шаг (см., напр.,

171

Рис. 61. Проективное свойство предложения

рис. 61, где правильна лишь конструкция слева). Про-

ведем проектирующие линии, соединяющие каждую

вершину дерева с его местом в предложении. Теперь

условие проективности можно сформулировать так:

ребра дерева зависимостей не пересекают друг друга

и не пересекают проектирующие линии. Оно дает

критерий для того, чтобы отличить правильные язы-

ковые конструкции от неправильных (в указанном

выше смысле).

2. Теоретико-множественная модель ИПС. Инфор-

мационно-поисковая система (ИПС) представляет со-

бой функциональную систему, предназначенную для

хранения и поиска информации. ИПС имеет запоми-

нающее устройство (хранилище), в котором располо-

жены документы (тексты, записи). Поиск информации—

это процесс отыскания в ИПС таких документов,

которые соответствуют поступившему запросу. Опе-

рации хранения и поиска неразрывно связаны друг

с другом. Именно поэтому они осуществляются в рам-

ках единой информационной системы—ИПС. Элемен-

тами реальной ИПС являются:

— множество (массив) документов, выступающих

в качестве объекта поиска;

— информационно-поисковый язык (ИПЯ)—искус-

ственный язык, предназначенный для описания содер-

жания и формы документов и запросов для после-

дующего осуществления поиска;

— правила индексирования, следуя которым про-

изводится описание средствами ИПЯ

документов и запросов (перевод с естественного

языка на ИПЯ); в результате индексирования

документа и запроса получаем поисковый образ

документа (ПОД) и поиско-

172

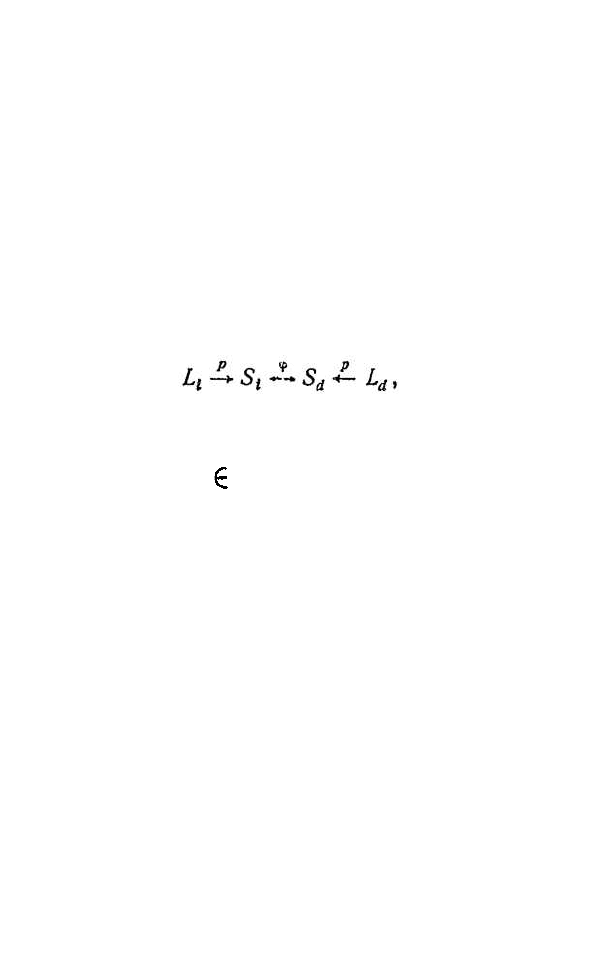
вое предписание (ПП) (или, что то же самое, поиско-

вый образ запроса ПОЗ):

— правила поиска документов, соответствующих

запросу, которые задаются в виде критерия соответ-

ствия (выдачи);

— технические средства и обслуживающий пер-

сонал.

Информационный запрос не включается в ИПС

и рассматривается как сигнал извне. Материальными

составляющими ИПС являются массивы документов,

технические средства и персонал. К семантическим

средствам относятся ИПЯ, методы индексирования

и поиска. С их помощью осуществляются смысловые

операции обработки документов и запросов и отбор

документов, подлежащих выдаче. Последовательность

этих операций схематически представляется в виде

где L

— текст запроса i на естественном языке, S

—

поисковое предписание, т. е. представление запроса на

ИПЯ с помощью функции индексирования р, L

—

текст документа d D на естественном языке, S

—

ПОД, т. е. представление документа на ИПЯ с

помощью функции индексирования р. Критерий

соответствия φ сопоставляет ПОД и ПП. Из указанной

схемы видно, что семантические операции сводятся к

моделированию смысла текста и к сравнению текстов на

ИПЯ. Таким образом, процесс информационного

поиска можно представить в виде следующей модели:

(D, 3, p: D→M

, p:3 →M

, φ: M

→M

включающей множества документов D, запросов 3,

поисковых образов документов M

, поисковых пред-

писаний М

и отношения между этими множествами,

задаваемые функцией индексирования р и критерием

соответствия φ. Опишем подробнее структуру и свой-

ства составляющих элементов этой модели.

Каждый документ, хранящийся в ИПС, имеет адрес

(поисковый номер), позволяющий идентифицировать

его в процессе поиска. Смысловое содержание доку-

мента описывается перечнем слов (индексов) ИПЯ,

образующих его поисковый образ. Количество слов

173

ИПЯ в ПОД может быть любым. Каждый элемент S

множества М

представляет собой множество S

, s

2 ...

, s

где s

...

—

слова ИПЯ. Оче

видно,

что любое слово ИПЯ может входить в несколько

ПОД, т. е. быть элементом нескольких множеств S

Между адресами документов (a

, а

, ..., а

) и словами

ИПЯ, образующими ПОД, существует два способа

взаимосвязи: при способе прямой организации

каждому адресу (a

) однозначно соответствует

множество S

; при инвертированной организации

каждому слову ИПЯ соответствует множество адре-

сов документов A

= {а

, а

, ..., a

}, в поисковые образы

которых входит данное слово. Оба эти способа

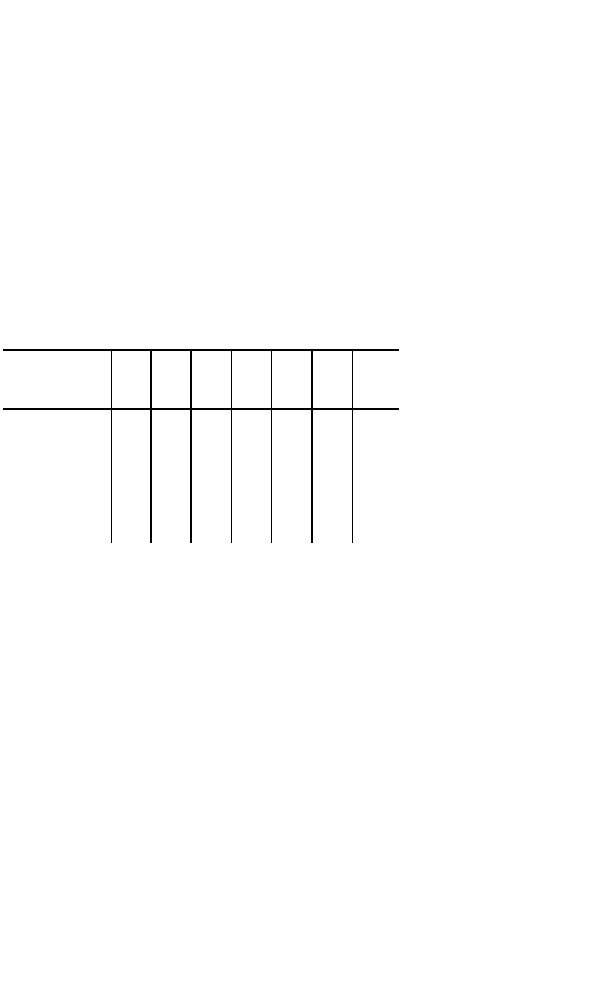
моделируются с помощью матрицы (табл. 34), где

Таблица 34

Адреса

документов

1 X

6 X X

словарь ИПЯ расположен по горизонтали (в данном

примере — из семи слов), а адреса документов — по

вертикали (здесь — шесть адресов). По отметкам

в матрице можно определить ПОД и адреса докумен-

тов, соответствующих тому или иному слову ИПЯ.

Прямая организация взаимосвязи соответствует на-

бору строк исходной матрицы, а инвентированная —

набору столбцов. Например, документ № 3 имеет

ПОД S

= {s

, s

}, а слову s

соответствует мно-

жество адресов А

={1, 2, 5}. В зависимости от спо-

соба организации различают прямые и инвертирован-

ные ИПС. Итак, дан теоретико-множественный спо-

соб описания ПОД. Описание ПП осуществляется

аналогично. Отличие состоит в том, что ПОД хра-

нится в ИПС, а ПП составляется только после по-

лучения запроса.

Для единого описания ИПЯ рассмотрим модель

ИПЯ как множества некоторых объектов, связанных

определенными отношениями. В информатике эти

174

основные элементы и отношения в ИПЯ называются

логико-лингвистическими универсалиями. К ним от-

носятся лексические единицы, парадигматические и

синтагматические отношения. Практически разнооб-

разие в представлении словарей и записей на ИПЯ

зависит от того, каким образом выбрано множество

лексических единиц и какие варианты группировки

этих единиц разрешаются в данном ИПЯ.

Лексическая единица (индекс, слово ИПЯ) — это

наименьшая осмысленная последовательность анаков,

задаваемая при конструировании ИПЯ. Другими сло-

вами, лексические единицы — это единицы смысла

в ИПЯ. План их содержания соответствует значению

отдельного слова или словосочетания естественного

языка или научному термину.

Парадигматические отношения представляют

смысловые связи лексических единиц и учитывают

сходство и различия в их содержании, т. е.

упорядочивают множество лексических единиц „по

вертикали". В качестве примера можно привести

отношения „род — вид", „целое — часть", „предмет —

свойство". На их основе лексические единицы

группируются в множества, называемые

парадигмами.

Синтагматические (текстуальные, грамматические,

синтаксические) отношения представляют семанти-

ческие отношения между лексическими единицами и

объединяют их в группы — синтагмы. Эти отношения

упорядочивают указанное множество по „горизонта-

ли", определяя порядок следования языковых элемен-

тов различного уровня.

Принципиальное отличие парадигматических и син-

тагматических отношений состоит в том, что первые

не зависят от каких-либо текстов, а вторые выража-

ют семантику контекста и зависят от нее.

Семантическая сила ИПЯ во многом определяется

мощностью базового множества (т. е. множества лек-

сических единиц). Пусть М

= {a

, ..., a

, ..., а

} —

лексика ИПЯ 1, М

= {b

, ..., b

} —

лексика ИПЯ 2, причем оба языка описывают одну и

ту же предметную область и мощность множества

существенно меньше мощности М

{m»п). Возьмем

два документа d

и d

, содержание которых

представляется набором понятий d

={p

, p

}, d

= {p

, p

}. Если в ИПЯ 1 для выражения понятий

175

, p

существует лишь одна лексическая

единица a

, то d

и d

получат один и тот же ПОД,

т.e. будут неразличимы при поиске. С другой сто-

роны, ИПЯ 2 дает возможность дифференцированно

представить каждое понятие, отражающее содержа-

ние d

и d

. При поиске на ИПЯ 2 документы будут

уже различимы и, следовательно, точность выдачи

выше.

Все реально существующие ИПЯ можно класси-

фицировать на основании теоретико-множественного

моделирования по трем основным логико-лингвисти-

ческим универсалиям (виды, характеристики и клас-

сификация ИПЯ, основанные на учете более широкого

спектра их свойств, изложены в ([22], гл. 4)).

1. По способу задания парадигматических отно-

шений выделяют в ИПЯ сильные и слабые отноше-

ния. Сильные отношения базируются на бинарном

отношении порядка, например, „род — вид", „выше —

ниже". Слабые отношения учитывают пересечения

понятий и ассоциации типа „целое—часть", „сходство".

Ведущую роль играют сильные парадигматические

отношения, слабые имеют вспомогательное значение

и в некоторых ИПЯ вообще отсутствуют. По разви-

тости сильных отношений различают;

— ИПЯ иерархической структуры, где все элементы

базового множества связаны отношением порядка.

Такие ИПЯ представляются древесным графом

(рис. 62). В терминах теории множеств основные

свойства иерархических классификаций записываются

следующим образом: пусть К — исходное множество

предметов, разбитое на основании некоторого приз-

нака на классы эквивалентности К

, К

, ..., К

(см. § 3).

Тем самым определяется иерархическое отношение

176

Рис. 62

Рис. 63. Граф фасетной классификации; А,

В, ..., Z—фасеты

между классом К и подклассами К

, К

, ..., К

. Далее

каждый из подклассов K

на основании другого при-

знака разбивается на классы эквивалентности и т. к.

— ИПЯ фасетной структуры. Базовое множество

разбивается на несколько групп (фасет), а внутри

каждой фасеты, представляющей собой множество

однородных терминов, связанных общностью какого-

либо признака, устанавливается иерархическая струк

тура. Следующие друг за другом в определенном

порядке фасеты образуют фасетную классификацию,

схематически изображенную на рис. 63;

— ИПЯ неиерархической структуры, в которых

сильными отношениями связаны только отдельные-

„пучки" лексических единиц. Упорядочение единиц,

в таких языках происходит по внешним признакам,

например, в алфавитном порядке.

Существует классификация ИПЯ по развитости

слабых парадигматических отношений. Она не имеет

теоретико-множественного описания, поэтому мы на

ней не останавливаемся. Отметим лишь, что иерархи-

ческие и фасетные ИПЯ близки к идеальным ИПЯ,

поскольку в них соблюдаются все важнейшие прави-

ла языка (однозначность, удобство пользования, вы-

ражение смысловых отношений и т. д.).

2. По способу задания базового множества (т. е.

лексики) ИПЯ различают:

— языки с контролируемой лексикой, где базовое

множество задается перечислительным способом

в виде словаря (таблиц классификации, рубрикатора,

информационно-поискового тезауруса), В иерархиче

ских и фасетных ИПЯ лексика контролируется

в обязательном порядке;

12 Т-743 177

— языки с неконтролируемой лексикой, в кото-

рых ограничиваются заданием правил использования

слов естественного языка. При этом возможны сле-

дующие варианты соответствия между лексическими

единицами ИПЯ и естественного языка;

a) s

≡ l

, i = 1, 2, ..., m, т. е. устанавливается

взаимно-однозначное соответствие между всеми еди-

ницами ИПЯ и некоторыми единицами естественного

языка;

б )s

= {l

(1)

, l

(2)

, ..., l

(п)

}, т. е. лексическая единица ИПЯ

передается фразой естественного языка;

в) l

Λ S

Λ ... Λ S

, т. е. лексические единицы

естественного языка представляются в виде конъ-

юнкций лексических единиц ИПЯ.

Случаи а) и б) называются первым и вторым уров-

нем интеграции естественного языка, а в) — случай

дезинтеграции. Опишем случай а) на языке множеств.

Ему соответствуют дескрипторные ИПЯ. Дескриптор—

это класс эквивалентных ключевых слов (т. е. слов

или устойчивых словосочетаний естественного языка).

Пусть L={l

, l

, ..., l

} — множество ключевых слов,

отобранных для данной ИПС. Задавая на L отноше-

ние эквивалентности, разбиваем его на множество

непустых непересекающихся классов эквивалентности,

каждый из которых является дескриптором. В резуль-

тате дескрипторизации множество L преобразуется

в множество D дескрипторов. Ясно, что L мощнее

D, т. к. из D исключены элементы, эквивалентные по

значению, однако однозначность дескрипторного ИПЯ

по сравнению с языком ключевых слов выше.

3. Средства выражения синтагматических отноше-

ний называются грамматикой ИПЯ. Если рассматри-

вать ПОД как текст на ИПЯ, то для фиксирования

грамматики нужно предусмотреть средства выделения

отдельных фрагментов (фраз, предложений), соответ-

ствующих законченным высказываниям, и указать

смысловую роль лексических единиц в этих фрагмен-

тах.

При фрагментировании указывают символ (букву,

цифру, знак пунктуации), приписываемый всем лекси-

ческим единицам ПОД, входящим в данный фрагмент, и

указывающий связи этих единиц. Например, если r

, ..., r

— указатели связи, то ПОД в некоторой

дескрипторной ИПС имеет вид (d

, r,

), (d

, r

178

, r

), ..., (d

, r

). Из этого выражения видно, что

дескрипторы d

и d

входят в один фрагмент ПОД, в

то же время d

совместно с d

входит в другой

фрагмент; совместно используются d

и d

. Отсутст-

вие или наличие фрагментирования, а также типы,

грамматик являются одними из критериев классифи-

каций ИПС.

Итак, на основании проведенного выше теоретико-

множественного анализа логико-лингвистических уни-

версалий ИПЯ построена классификация поисковых

языков по признакам тех или иных частей общей,

теоретико-множественной модели ИПЯ. Теперь нам

необходимо описать отношения (функцию индексиро-

вания и критерии соответствия), входящие как эле-

менты в теоретико-множественную модель ИПС.

Цель процесса индексирования в ИПС — приписать

каждой единице хранения некоторое множество иден-

тификаторов, отражающих содержание документов.

Способы индексирования с применением методов

математической логики были описаны ранее в § 6

(см. также [22], гл. 4, п. 5). Обычно процесс индекси-

рования включает в себя одну или несколько из сле-

дующих операций:

— отбор терминов (дескрипторов п т. д.), харак

теризующих содержание данного документа;

— приписывание этим терминам некоторого веса,

отражающего их предполагаемую важность;

— отнесение каждого термина к определенному

классу свойств, объектов и т. д.;

— определение отношений между терминами (си

нонимических, лексикографических, иерархических и

т. д.).

Если ПОД состоит из одной лексической единицы

ИПЯ, например, одного классификационного индекса,

то имеем одноаспектное индексирование. Пусть D

= {d

, d

, ..., d

} —множество документов, в котором

производится поиск, a S= {s

, s

, ..., s

} —лексический

состав ИПЯ. При многоаспектном индексировании

каждому документу однозначно соответствует

некоторый набор лексических единиц из S, образую-

щих ПОД. Иными словами, элементы множества D

отображаются в множество S: d

→ ПОД = {s

, s

..., ..., s

}. В множестве D может содержаться

несколько документов, имеющих одинаковый образ в

S. Поэто-

12* 179

му нужно говорить об отображении в S не отдель-

ных документов, а соответствующих подмножеств D.

Опишем с точки зрения математики содержание вве-

денных выше операций индексирования (о показателях

эффективности индексирования см. [22], гл. 3, п. 4).

Отбор терминов производится, как правило, сле-

дующим образом: выписываются слова, встречающиеся

в каждом документе, и делаются определённые

статистические подсчеты, в основе которых лежит

частота появления данного слова в документах или

вo всем массиве. Далее, отбрасываются общеупотре-

бительные слова, имеющие высокую частоту, а остав-

шимся словам приписываются веса в соответствий

с ранее проведенными статистическими расчетами.

Можно вводить также некоторые уточнения, объеди-

няя термины в группы или указывая связи между

ними. Адекватность данного термина для отражения

содержания документа не может быть достаточно

убедительно установлена в результате рассмотрения

терминов одного отдельно взятого документа. Поэ-

тому нужно описать поведение документа в полном

фонде.

Среди теорий индексирования, учитывающих всю

совокупность документов, рассмотрим сначала модель,

основанную на частотности. Её идея состоит в том,

чтобы отдавать предпочтение терминам, которые

встречаются с высокой частотой в отдельных доку-

ментах фонда, в то время как суммарная частота их

появления в фэнде довольно невелика. Впервые та-

кую модель исследовал X. Лун, вводя частотные

меры: f

— частота появления термина k в документе

, F

= f

— суммарная частота термина k в наборе

документов. Для усовершенствования частотных

мер можно использовать относительные частотные

параметры, чтобы частоту появления термина в дан-

ном набора можно было сравнить с частотой его

появления во всем объеме литературы. Однако прак-

тическое использование этих параметров затрудняется

тем, что нелегко обработать „всю литературу". В мо-

дели, дополняющей предыдущую и созданной Спарк

Джоунс, делается акцент на отбрасывание нерелевант-

ных документов. Точнее, если определить докумен-

180