Everitt B.S. The Cambridge Dictionary of Statistics

Подождите немного. Документ загружается.

Joint distribution: Essentially synonymous with

multivariate distribution

, although used particu-

larly as an alternative to

bivariate distribution

when two variables are involved. [KA1

Chapter 6.]

Jolly^Seber model: A model used in

capture-recapture

sampling which allows for capture prob-

abilities and survival probabilities to vary among sampling occasions, but assumes these

probabilities are homogeneous among individuals within a sampling occasion. [Biometrics,

2003, 59, 786–794.]

Jonckheere, Aimable Robert (1920^2005): Born in Lille in the north of France, Jonckheere

was educated in England from the age of seven. On leaving Edmonton County School he

became apprenticed to a ﬁrm of actuaries. As a paciﬁst, Jonckheere was forced to spend the

years of World War II as a farmworker in Jersey, and it was not until the end of hostilities that

he was able to enter University College London, where he studied psychology. But

Jonckheere also gained a deep understanding of statistics and acted as statistical collaborator

to both Hans Eysenck and Cyril Burt. He developed a new statistical test for detecting trends

in categorical data and collaborated with Jean Piaget and Benoit Mandelbrot on how

children acquire concepts of probability. Jonckheere died in London on 24 September 2005.

Jonckheere’s k-sample test: A

distribution free method

for testing the equality of a set of

location parameters against an

ordered alternative hypothesis

.[Nonparametrics:

Statistical Methods Based on Ranks, 1975, E. L. Lehmann, Holden-Day, San Francisco.]

Jonckheere^Terpstra test: A test for detecting speciﬁc types of departures from independence

in a

contingency table

in which both the row and column categories have a natural order (a

doubly ordered contingency table

). For example, suppose the r rows represent r distinct drug

therapies at progressively increasing drug doses and the c columns represent c ordered

responses. Interest in this case might centre on detecting a departure from independence in

which drugs administered at larger doses are more responsive than drugs administered at

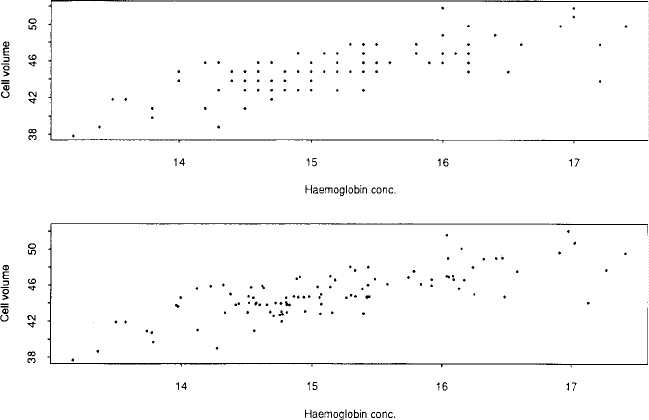
Fig. 75 An example of ‘jittering’: ﬁrst scatterplot shows raw data; second scatterplot shows data after

being jittered.

229

smaller ones. See also linear-by-linear association test.[Biostatics: A Methodology for the

Health Sciences, 2nd edn, 2004, G. Van Belle, L. D. Fisher, P. J. Heagesty and T. S. Lumley,

Wiley, New York.]

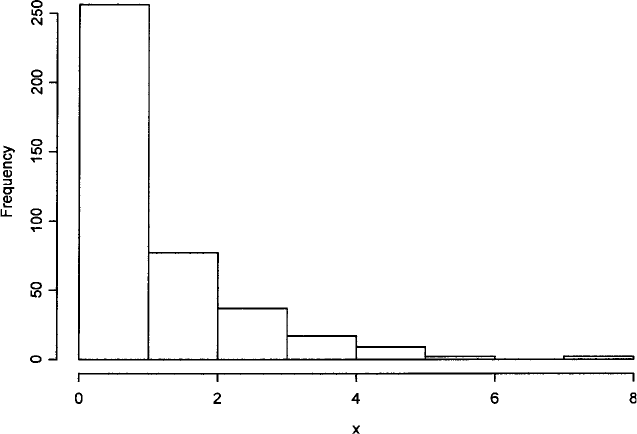
J-shaped distribution: An extremely

asymmetrical distribution

with its maximum frequency in

the initial (or ﬁnal) class and a declining or increasing frequency elsewhere. An example is

given in Fig. 76.

Just identified model: See identiﬁcation.

Fig. 76 An example of a J-shaped frequency distribution.

230

, k

)-design: An unbalanced design in which two measurements are made on a sample of k

individuals and only a single measurement made on a further k

individuals.

Kalman filter: A recursive procedure that provides an estimate of a signal when only the ‘noisy

signal’ can be observed. The estimate is effectively constructed by putting exponentially

declining weights on the past observations with the rate of decline being calculated

from various variance terms. Used as an estimatio

n technique in the analysis of

time series

data. [TMS Chapter 10.]

Kaiser’srule: A rule often used in

principal components analysis

for selecting the appropriate number

of components. When the components are derived from the

correlation matrix

of the

observed variables, the rule suggests retaining only those components with eigenvalues

(variances) greater than one. See also scree plot.[Educational and Psychological

Measurement, 1960, 20, 141–51.]

Kaplan ^ Mei er esti mator: Synonym for product limit estimator.

Kappa coefficient: A chance corrected index of the

agreement

between, for example, judgements

and diagnoses made by two raters. Calculated as the ratio of the observed excess over chance

agreement to the maximum possible excess over chance, the coefﬁcient takes the value

one when there is perfect agreement and zero when observed agreement is equal to chance

agreement. See also Aickin’s measure of agreement. [SMR Chapter 14.]

Kar b er method: A nonparametric procedure for estimating the

median effective dose

in an

quantal assay. [Encyclopedia of Statistical Sciences, 2006, eds. S. Kotz, C. B. Read,

N. Balakrishnan and B. Vidakovic, Wiley, New York.]

KDD: Abbreviation for knowledge discovery in data bases.

K el lerer, H ans ( 1902^1 976): Born in a small Bavarian village, Kellerer graduated from the

University of Munich in 1927. In 1956 he became Professor of Statistics at the University

of Munich. Kellerer played an important role in getting modern statistical methods accepted

in Germany.

K empthorne, Oscar ( 1 91 9^2000): Born in Cornwall, England, Kempthorne studied at

Cambridge University where he received both B.A. and M.A. degress. In 1947 he joined

the Iowa State College statistics faculty where he remained an active member until his

retirement in 1989. In 1960 Kempthorne was awarded an honorary Doctor of Science

degree from Cambridge in recognition of his contributions to statistics in particular to

experimental design

and the

analysis of variance

. He died on 15 November 2000 in

Annapolis, Maryland.

Kempton, Rob (194 6^20 03): Born in Isleworth, Middlesex, Kempton read mathematics at

Wadham College, Oxford. His ﬁrst job was as a statistician at Rothamsted Experimental

Station, and in 1976 he was appointed Head of Statistics at the Plant Breeding Institute in

231

Cambridge where he made contributions to the design and analysis of experiments with

spatial trends and treatment

carryover effects

. In 1986 Kempton became the founding

director of the Scottish Agricultural Statistics Service where he carried out work on the

statistical analysis of health risks from food and from genetically modiﬁed organisms.

He died on 11 May 2003.

Kendall’s coefficient of concordance: Synonym for coefﬁcient of concordance.

Kendall, Sir Maurice George (1907^1983): Born in Kettering, Northamptonshire, Kendall

studied mathematics at St John’s College, Cambridge, before joining the Administrative

Class of the Civil Service in 1930. In 1940 he left the Civil Service to become Statistician

to the British Chamber of Shipping. Despite the obvious pressures of such a post in war

time, Kendall managed to continue work on The Advanced Theory of Statistics which

appeared in two volumes in 1943 and 1946. In 1949 he became Professor of Statistics

at the London School of Economics where he remained until 1961. Kendall’s main work

in statistics involved the theory of k

-statistics

time series

and

rank correlation methods

He also helped organize a number of large sample survey projects in collaboration with

governmental and commercial agencies. Later in his career, Kendall became Managing

Director and Chairman of the computer consultancy, SCICON. In the 1960s he completed

the rewriting of his major book into three volumes which were published in 1966. In

1972 he became Director of the World Fertility Survey. Kendall was awarded the Royal

Statistical Society’s Guy Medal in gold and in 1974 a knighthood for his services to the

theory of statistics. He died on 29 March 1983 in Redhill, UK.

Kendall’s tau statistics: Measures of the correlation between two sets of rankings. Kendall’s tau

itself (τ) is a rank correlation coefﬁcient based on the number of inversions in one ranking as

compared with another, i.e. on S given by

S ¼ P  Q

where P is the number of concordant pairs of observations, that is pairs of observations

such that their rankings on the two variables are in the same direction, and Q is the number

of discordant pairs for which rankings on the two variables are in the reverse direction.

The coefﬁcient τ is calculated as

τ ¼

nðn 1Þ

A number of other versions of τ have been developed that are suitable for measuring

association in an r×c

contingency table

with both row and column variables having

ordered categories. (Tau itself is not suitable since it assumes no tied observations.) One

example is the coefﬁcient, τ

given by

2mS

ðm 1Þ

where m ¼ minðr; cÞ. See also phi-coefﬁcient, Cramer’sVand contingency coef ﬁcient.

[SMR Chapter 11.]

Kernel density estimators: Methods of estimating a probability distribution using estimators

of the form

f ðxÞ¼

i¼1



x  X



232

where h is known as window width or bandwidth and K is the kernel function which

is such that

1

KðuÞdu ¼ 1

Essentially such kernel estimators sum a series of ‘bumps’ placed at each of the observa-

tions. The kernel function determines the shape of the bumps while h determines their width.

Three commonly used kernel functions are

Rectangular: K(x) = 0.5 if |x| < 1 and K(x) = 0 otherwise

Triangular: K(x)=1− |x|if|x| < 1 and K(x) = 0 otherwise

Gaussian: KðxÞ¼

ﬃﬃﬃﬃﬃﬃ



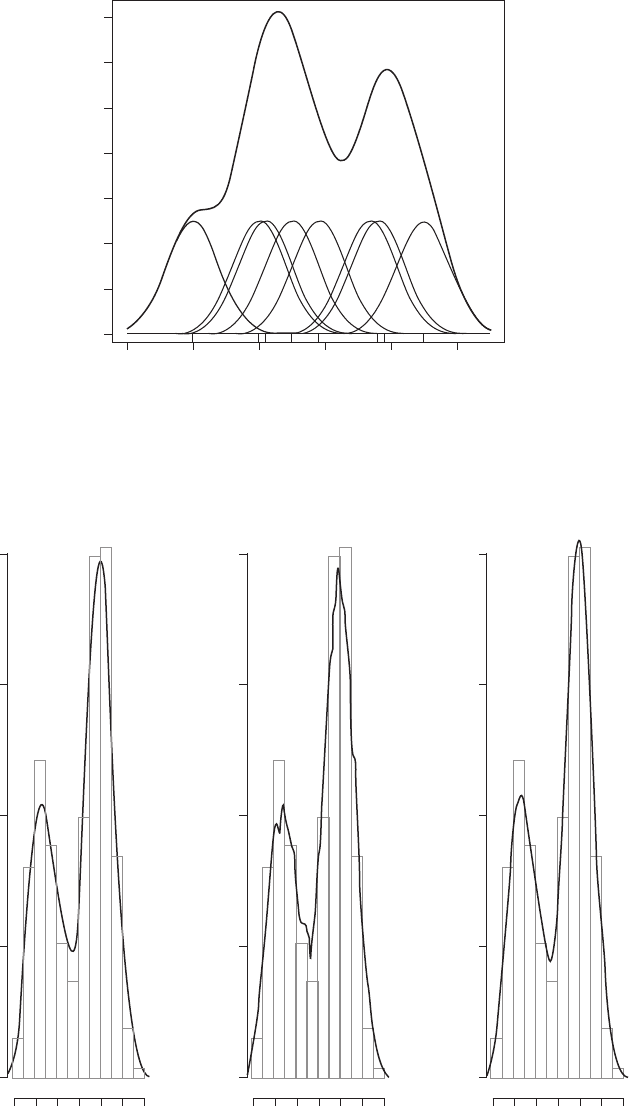
The three kernel functions are shown in Figure 77 The kernel estimator is a series of

‘bumps’ placed at the observations, with the kernel function determining the shape of the

bumps and the window width h determining their width. Figure 78 shows the individual

bumps and the estimate,

f , obtained from adding them up for an artiﬁcial set of data points

using a Gaussian kernel. The extension of kernel density estimation from univariate

situations to multivariate data is relatively straightforward. An example of the application

of the method to univariate data on waiting times between two eruptions of the Old

Faithful geyser in Yellowstone National Park is shown in Figure 79, and a bivariate

example using data on body measurements is given in Figure 80. [Density Estimation in

Statistics and Data Analysis, 1986, B. Silverman, Chapman and Hall/CRC Press, London.]

Kernel estimators: See kernel density estimators.

K erne l functi o n: See kernel density estimators.

K erne l regressi on smooth i ng: A

distribution free method

for smoothing data. In a single

dimension, the method consists of the estimation of f ðx

Þ in the relation

¼ f ðx

Þþe

where e

; i ¼ 1; ...; n are assumed to be symmetric errors with zero means. There are

several methods for estimating the regression function, f, for example, averaging the y

0.0

–3 –2 –1 0 1 2 3

Kernel functions

Rectangular

Triangular

Gaussian

0.2 0.4 0.6

K(x)

0.8 1.0

Fig. 77 Three

commonly used kernel

functions.

233

0.350.300.250.200.150.100.050.00

–1 0 1

234

f(x)

Fig. 78 Kernel estimate

showing the contributions

of Gaussian kernels

evaluated for the

individual observations

with bandwidth h=0.4.

0.040.030.02

Frequency

0.010.00

0.040.030.02

Frequency

0.010.00

0.040.030.02

Frequency

0.010.00

6040 80

Waitin

times (in min.)

Gaussian kernel Rectangular kernel Triangular kernel

100 6040 80

Waitin

times (in min.)

100 6040 80

Waitin

times (in min.)

100

Fig. 79 Three density estimates of the geyser eruption data imposed on a histogram of the data.

234

values that have x

close to x. See also regression modelling.[Transformation and

Weighting in Regression, 1988, R. J. Carroll and D. Ruppert, Chapman and Hall/CRC

Press, London.]

Khamis, Salem (1 91 9^20 05): Born in a small village in the Nazareth district of Palestine,

Khamis graduated with a BA in mathematics and an MA in physics both from the

American University of Beirut. On receiving a British Council Fellowship he travelled

to England to undertake doctoral studies in statistics at University College, London.

Khamis spent much of his working life as an international civil servant for the United

Nations but he made signiﬁcant contributions to statistics in the areas of sampling

theory and, in particular, the computation of purchasing power parities (PPPs) of

currencies for the conversion of national currency-dominated economic aggregates,

like gross domestic product, into a common comparable currency unit; the most well

known PPP is the

Big Mac Index

. Khamis was vice-president of the International

Statistical Institute from 1979–1981. He died in Hemel Hempsted, England on the

16th June 2005.

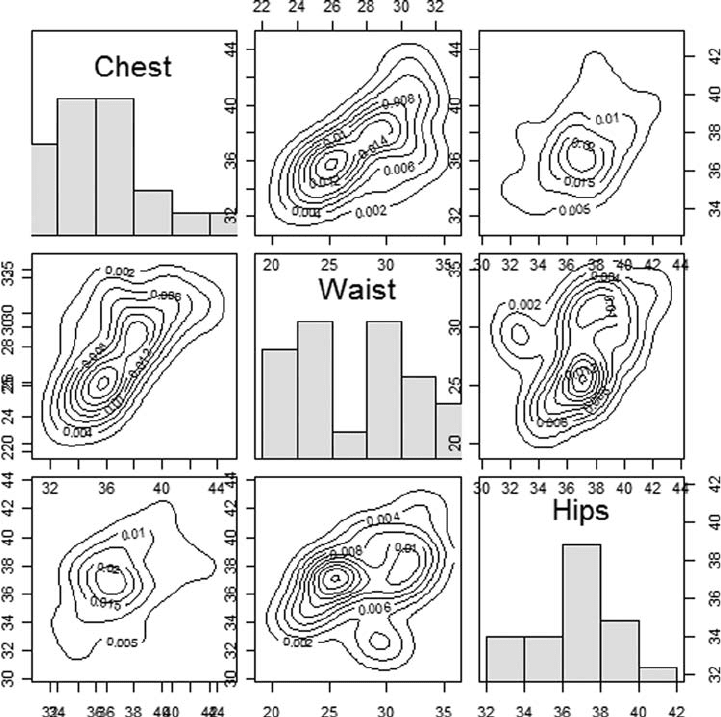
Fig. 80 Scatterplot matrix of three body measurements on 20 individuals showing bivariate density

estimates on each panel and histograms on main diagonal.

235

Khinchin theorem: If x

; ...; x

is a sample from a probability distribution with expected

value μ then the sample mean converges in probability to μ as n !1. [KA1

Chapter 14.]

Kish, Leslie (1910^2000): Born in Poprad at the time it was part of the Austro-Hungarian Empire

(it is now in Slovakia), Kish received a degree in mathematics from the City College of

New York in 1939. He ﬁrst worked at the Bureau of the Census in Washington and later

at the Department of Agriculture. After serving in the war, Kish moved to the University

of Michigan in 1947, and helped found the Institute for Social Research. During this

period he received both MA and Ph.D degrees. Kish made important and far reaching

contributions to the theory of sampling much of it published in his pioneering book

Survey Sampling. Kish received many awards for his contributions to statistics including

the Samuel Wilks Medal and an Honorary Fellowship of the ISI.

Kitagawa,Tosio (1909^1993): Born in Otaru City, Japan, Kitagawa studied in the Department

of Mathematics at the University of Tokyo for where he graduated in 1934. And in 1934

he was awarded a Doctorate of Science from the same university for his work on func-

tional equations. In 1943 he became the ﬁrst professor of mathematical statistics in Japan

and in 1948–1949 was acting director of the Institute of Statistical Mathematics in Tokyo.

Kitagawa made contributions in

statistical quality control, sample survey theory

and

design of experiments

. He died on March 13th, 1993 in Tokyo.

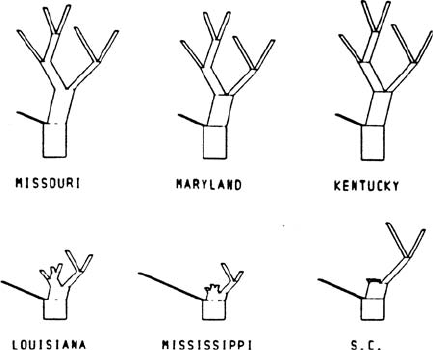
Kleiner^Hartigan trees: A method for displaying

multivariate data

graphically as ‘trees’ in

which the values of the variables are coded into the length of the terminal branches and

the terminal branches have lengths that depend on the sums of the terminal branches they

support. One important feature of these trees that distinguishes them from most other

compound characters, for example,

Chernoff’s faces

, is that an attempt is made to remove

the arbitrariness of assignment of the variables by performing an

agglomerative hierarch-

ical cluster analysis

of the variables and using the resultant

dendrogram

as the basis tree.

Some examples are shown in Fig. 81.[Journal of the American Statistical Association,

1981, 76, 260 –9.]

Klotz test: A

distribution free method

for testing the equality of variance of two populations having

the same median. More efﬁcient than the

Ansari–Bradley test

. See also Conover test.

[Encyclopedia of Statistical Sciences, 2006, eds. S. Kotz, C. B. Read, N. Balakrishnan and

B. Vidakovic, Wiley, New York.]

Fig. 81 Kleiner–Hartigan

trees for Republican vote data

in six Southern states.

236

K-m eans cluste ran alysis: A method of

cluster analysis

in which from an initial partition of the

observations into K clusters, each observation in turn is examined and reassigned, if

appropriate, to a different cluster in an attempt to optimize some predeﬁned numerical

criterion that measures in some sense the ‘quality’ of the cluster solution. Many such

clustering criteria have been suggested, but the most commonly used arise from consid-

ering features of the

within groups

between groups

and

total matrices of sums of squares

and cross products

(W, B, T) that can be deﬁned for every partition of the observations

into a particular number of groups. The two most common of the clustering criteria arising

from these matrices are

minimization of trace WðÞ

minimization of determinant W

ðÞ

The ﬁrst of these has the tendency to produce ‘spherical’ clusters, the second to produce

clusters that all have the same shape, although this will not necessarily be spherical. See also

agglomerative hierarchical clustering methods, divisive methods and hill-climbing

algorithm. [MV2 Chapter 10.]

K-means inverse regression: An extension of

sliced inverse regression

multivariate regres-

sion

with any number of response variables. The method may be particularly useful at the

‘exploration’ part of an analysis, before suggesting any speciﬁc multivariate model.

[Technometrics, 2004, 46, 421–429.]

Knots: See spline functions.

Knowl edge discovery i n data bases (K DD) : A form of

data mining

which is interactive

and iterative requiring many decisions by the researcher. [Communication of the ACM,

1996, 39 (II),27–34.]

Knox’stests: Tests designed to detect any tendency for patients with a particular disease to form a

disease cluster

in time and space. The tests are based on a

two-by-two contingency table

formed from considering every pair of patients and classifying them as to whether the

members of the pair were or were not closer than a critical distance apart in space and as to

whether the times at which they contracted the disease were closer than a chosen critical

period. [ Statistics in Medicine, 1996, 15, 873–86.]

Kolmogorov,AndreiNikolaevich(1903^1987): Born in Tambov, Russia, Kolmogorov ﬁrst

studied Russian history at Moscow University, but turned to mathematics in 1922. During

his career he held important administrative posts in the Moscow State University and the

USSR Academy of Sciences. He made major contributions to probability theory and

mathematical statistics including laying the foundations of the modern theory of Markov

processes. Kolmogorov died on 20 October 1987 in Moscow.

Kolmogorov^Smirnov two-sample method: A

distribution free method

that tests for any

difference between two population probability distributions. The test is based on the

maximum absolute difference between the

cumulative distribution functions

of the

samples from each population. Critical values are available in many statistical tables.

[Biostatistics: A Methodology for the Health Sciences, 2nd edn, 2004, G. Van Belle,

L. D. Fisher, P. J. Heagerty and T. S. Lumley, Wiley, New York.]

Korozy, Jozsef (1844^1906): Born in Pest, Korozy worked ﬁrst as an insurance clerk and

then a journalist, writing a column on economics. Largely self-taught he was appointed

director of a municipal statistical ofﬁce in Pest in 1869. Korozy made enormous

contributions to the statistical and demographic literature of his age, in particular

237

developing the ﬁrst fertility tables. Joined the University of Budapest in 1883 and

received many honours and awards both at home and abroad.

Kovacsics, Jozsef (1919^2003): Jozsef Kovacsics was one of the most respected statisticians

in Hungary. Starting his career in the Hungarian Statistical Ofﬁce, he was appointed

Director of the Public Library of the Statistical Ofﬁce in 1954 and in 1965 became a full

professor of statistics at the Eotvos Lorand University where he stayed until his retirement

in 1989. Kovacsics carried out important work in several areas of statistics and

demo-

graphy

. He died on 26 December 2003.

KPSS test: Abbreviation for the Kwiatkowski-Phillips-Schmidt-Shin test.

Kriging: A method for providing the value of a random process at a speciﬁed location in a region,

given a dataset consisting of measurements of the process at a variety of locations in the

region. For example, from the observed values y

; y

; ...; y

of the concentration of a

pollutant at n sites, t

; t

; ...; t

, it may be required to estimate the concentration at a

new nearby site, t

. Named after D. G. Krige who ﬁrst introduced the technique to estimate

the amount of gold in rock. [Interpolation for Spatial Data: Some Theory for Kriging,

1999, M. L. Stein, Springer, New York.]

Kronecker product of matrices: The result of multiplying the elements of an m×mmatrix A

term by term by those of an n×nmatrix B. The result is an mn × mn matrix. For example, if

A ¼



and B ¼

147

258

369

then

B ¼

1472814

2 5 8 4 10 16

3 6 9 6 12 18

3 12 21 4 16 28

6 10 16 8 20 32

91827122436

B is not in general equal to B

A: [MV1 Chapter 2.]

Kruskal ^ Wallis test: A

distribution free method

that is the analogue of the

analysis of variance

of a

one-way design

. It tests whether the groups to be compared have the same population

median. The test statistic is derived by ranking all the N observations from 1 to N regardless

of which group they are in, and then calculating

H ¼

i¼1







RÞ

NðN  1Þ

where n

is the number of observations in group i,



is the mean of their ranks,



R is the

average of all the ranks, given explicitly by ðN þ 1Þ=2. When the null hypothesis is true the

test statistic has a

chi-squared distribution

with k  1 degrees of freedom. [SMR Chapter 9.]

k-statistics: A set of symmetric functions of sample values proposed by

Fisher

,deﬁned by

requiring that the pth k-statistic, k

, has expected value equal to the pth

cumulant

, 

, i.e.

Eðk

Þ¼

Originally devised to simplify the task of ﬁnding the

moments

of sample statistics. [KA1

Chapter 12.]

238