Galaktionov V.A., Svirshchevskii S.R. Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics
Подождите немного. Документ загружается.


3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 153
0 1 2 3 4 5 6 7
−5
−4
−3
−2
−1
0
1
2
3
4
5
x 10
−4
s
φ(s)
φ
0
−φ
0
(a) n =
1
2
,λ= 1
0 1 2 3 4 5 6 7
−6
−4
−2
0
2
4
6
x 10
−6
s
φ(s)
(b) n =
1
2
,λ=−1
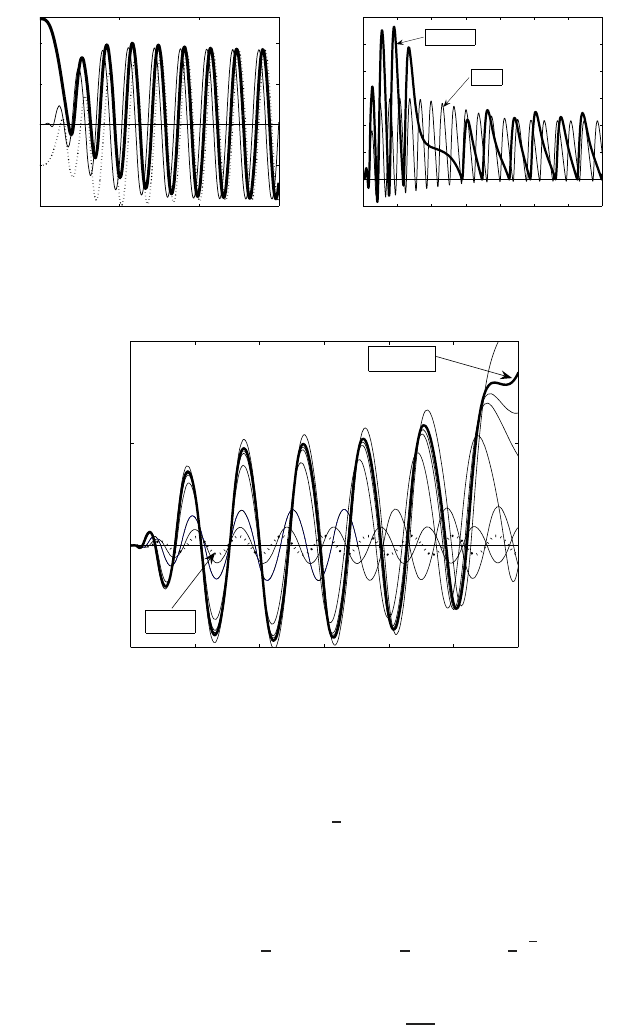
Figure 3.17 Solutions of the ODE (3.191) with n =
1
2
in the stabilization case λ = 1 (a) and
in the oscillatory case λ =−1(b).
The operator [v] is monotone in the topology of the Hilbert space H
−4
(IR ).Ex-
istence and uniqueness of weak continuous solutions are based on general theory of
tions, it is not difficult to check that, for a specialclass of sufficiently regular (strong)
weak solutions {u(x, t)}, there exists a limit as n → 0
+
, establishing a homotopic
(non-singular) connection with the linear bi-harmonic PDE (3.2) in IR × IR
+
.The
uniform convergence of strong solutions as n → 0
+
is an important property that
will be used later on. For (3.188), the TWs satisfy
| f |
n
f
(4)
= λf
for y > 0, f (0) = 0,
so that, instead of the change (3.186),
f (y) = y
γ
ϕ(s), s = ln y, with γ =
3
n
, where (3.190)
ϕ
(4)
+ 2(2γ − 3)ϕ
+ (6γ
2
− 18γ + 11)ϕ
+ 2(2γ
3
− 9γ
2
+11γ − 3)ϕ
+ γ(γ − 1)(γ − 2)(γ − 3)ϕ =
λ
|ϕ|
n
(ϕ
+ γϕ).
(3.191)
This ODE has two equilibria
±ϕ
0
=±
λ
(γ −1)(γ −2)(γ −3)
1
n
. (3.192)
They exist in the parameter ranges n ∈
1,
3
2
and n > 3ifλ<0, and for n ∈ (0, 1)
and n ∈
3
2
, 3
if λ>0.
Figure 3.17 shows different behavior of solutions in the case of n =
1
2
for λ>0
(convergenceto the positive constant equilibria (3.192); no traces of stable or unsta-
ble periodic patterns were observed) and for λ<0 (oscillatory). Periodic patterns
ϕ(s) persist for larger n, including n = 1.1; see Figure 3.18. Further increasing n,a
few oscillations appear followed by fast divergence of the solution ϕ(s), according
to the linear unstable exponential bundle.
Subcritical bifurcation. Numerically, the constant equilibrium ϕ
0
of (3.191) be-
comes asymptotically stable for n > n
st
,where
n
st
= 1.287...
© 2007 by Taylor & Francis Group, LLC
monotone operators; see Lions [396, Ch. 2]. Writing (3.189) in the sense of distribu-
154 Exact Solutions and Invariant Subspaces
0 5 10 15
−0.1
−0.05
0
0.05
0.1
s
φ(s)
(a) n = 0.9
0 10 20 30 40 50 60 70
−2
0
2
4
6
8
10
12
s
φ(s)
n=1.1
n=1.12755
(b) n = 1.1and1.12755
Figure 3.18 Convergence to stable periodic solutions of the ODE (3.191), λ =−1, with
various Cauchy data at s = 0forn = 0.9 (a) and n = 1.1, n = 1.12755 (b).
0 5 10 15 20 25 30
−500
0
500
1000
s
φ(s)
n=1.287
n=1.2
Figure 3.19 Behavior as n → n
−
st
of solutions of the ODE (3.191), with λ =−1.
and as n → n
−
st
, the stable periodic solution becomes nonexistent,as shown in Figure
3.19. Therefore, for n > n
st
, the TW profiles are no longer oscillatory near such
interfaces (only a finite number of zeros is available). Such non-oscillatory behavior
becomes more and dominant for larger n >
3
2
, so that, possibly, the Cauchy problem
can be posed in the class of nonnegative solutions; an
OPEN PROBLEM.
Extra scaling for small n > 0. As usual, to see the oscillatory patterns for small
n > 0, an extra scaling in (3.191) with λ =−1 is performed by setting
ϕ(s) = Aψ(η), η =
s
a
, where a =
n
3
and A =
n
3
3
n
.
This leads to the simplified equation with a linear binomial operator,
ψ
(4)
+ 4ψ
+ 6ψ
+ 4ψ
+ ψ =−
1
|ψ|
n
(ψ
+ ψ), (3.193)
where we omit terms of the order O(n). In Figure 3.20, a stable periodic behavior
© 2007 by Taylor & Francis Group, LLC
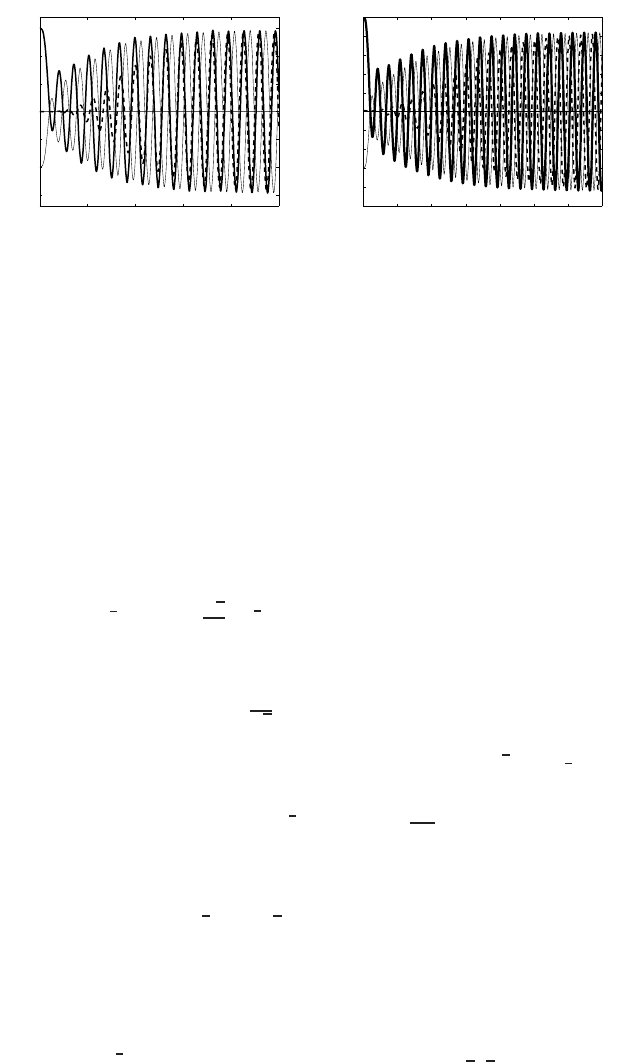
3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 155
0 10 20 30 40 50
−1.5
−1
−0.5
0
0.5
1
1.5
x 10
−3
η
ψ(η)
(a) n = 0.3
0 10 20 30 40 50 60 70
−5
−4
−3
−2
−1
0
1
2
3
4
5
x 10
−5
η
ψ(η)
(b) n = 0.2
Figure 3.20 Stable periodic behavior for (3.193) for n = 0.3 (a) and n = 0.2(b).
of the ODE (3.193) is shown. For n = 0.2, the periodic solution is very small,
max|ϕ|∼10
−22
.
Comparison with the linear PDE. In view of the continuity at n = 0
+
, consider the
PDE (3.2) that admits TWs with the profiles satisfying
λf = f
⇒ f (y) = e
µy
, where µ
3
= λ.
We are interested in the behavior as y →−∞which is the left-hand “interface”
for solutions of the linear equation. Then, taking λ>0 gives the only possible non-
oscillatory exponential behavior
f (y) ∼ e
λ
1/3
y
as y →−∞.
On the contrary, for λ<0, oscillatory patterns are obtained,
f (y) ∼ e
1
2
|λ|
1/3
y
cos
√
3
2
|λ|
1
3
y + A
0
, where A
0
= constant. (3.194)
This is in qualitative agreementwith the properties of the nonlinear ODE (3.191) for
n ∈ (0, 1]. It is curious that the period of linear oscillations in (3.194),
T
n=0
=
4π
√
3
= 7.26... (λ =−1),
is comparable with the nonlinear ones in Figure 3.17(b), for n =
1
2
, T
n=
1
2
≈ 1.3.
The fundamental solution of the bi-harmonic equation (3.2),
b(x, t) = t
−
1
4
F(ζ ), ζ =
x
t
1/4
,
correspondsto the case λ>0aty =+∞. The rescaled kernel F is the unique radial
solution of the ODE problem
−F
(4)
+
1
4
ζ F
+
1
4
F = 0inIR ,
F = 1.
Then F = F(|ζ |) has exponential decay and oscillates as |ζ |→∞; general es-
timates on fundamental solutions can be found in Eidelman [164, p. 115]. More
precisely, using standard asymptotic expansion yields the following behavior of the
kernel as ζ →+∞:
F(ζ ) ∼ ζ
−
1
3
e
aζ
4/3
, with complex a satisfying a
3
=
1
4
3
4
3
, Rea < 0.
© 2007 by Taylor & Francis Group, LLC
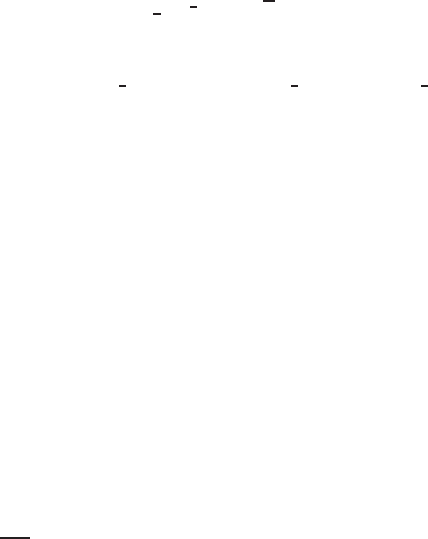
156 Exact Solutions and Invariant Subspaces
There exist two complex conjugate roots for exponentially decaying profiles
a
±
=−
3
8
4
−
1
3
(1 ± i
√
3) ≡−c
1
± ic
2
.
This yields the following oscillatory behavior as ζ →+∞:
F(ζ ) ∼ ζ
−
1
3
e
−c
1
ζ
4/3
A
1
cos
c
2
ζ
4
3
+ A
2
sin
c
2
ζ
4
3
, (3.195)
where A
1
and A
2
are constants. The algebraic factorζ
−1/3
is obtained by the WKBJ-
type technique. This is a periodic behavior with a single fundamental frequency. We
have seen numericallythat such a stableperiodicstructureis inheritedin the behavior
(3.190) for all n ∈ (0, n
h
).
Example 3.38 (Finite propagation and changing sign behavior in higher-order
semilinear models)Aswehaveseen,finite propagation and oscillatory solutions of
the CP can beobtained in any semilinear parabolic models by adding a non-Lipschitz
absorption-like term, e.g., (see [227] for properties and ε-regularization)
u
t
= F[u] ≡ (−1)
m+1
D
2m
x
u −|u|
p−1
u, with p ∈ (−1, 1). (3.196)
For TWs, there occurs the ODE
−λf
= F[ f ]fory > 0, f (0) = 0,
which, close to the finite interface, becomes asymptotically stationary,
(−1)
m+1
f
(2m)
−|f |
p−1
f = 0 ⇒ f (y) = y
γ
ϕ(ln y), (3.197)
where γ =
2m
1−p
> 0. For anym ≥ 2, such ODEs have oscillatory solutions; see Sec-
tion 3.7. Note that (3.196) also describes the phenomenon of finite-time extinction
proved by energy estimates based on Saint–Venant’s principle; see [524] and survey
in [240]. The range p ≤−1 corresponds to nonexistence, [227].
Similarly, equations of Cahn–Hilliard type with mass conservation
u
t
= F[u] ≡ (−1)
m+1
D
2m
x
u − D
2k
x
|u|
p−1
u
for 1 ≤ k < m,
can also admit finite propagation. Solutions of changing sign (for k ≤ m − 2) are
given by (3.197) with 2m → 2(m −k). Depending on m and k, theperiodic behavior
of ϕ(s) can be stable or unstable, as in the examples discussed above.
3.9 Quasilinear pseudo-parabolic models: the magma equation
A typical pseudo-parabolic model to be studied is
u
t
=
u
n
u
t
xx
+ (lower-order terms)(u ≥ 0), (3.198)
where n ∈ IR is a fixed exponent. Such PDEs arise in mathematical modeling of the
segregation and migration of magma in the mantle of the Earth, [519, 420]. The full
model, called the magma equation,is
u
t
=
(u
n
u
t
)
x
− 1
u
l
x
, (3.199)
© 2007 by Taylor & Francis Group, LLC
3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 157
with two parameters n and l. Setting l = 0 gives the principal operator in (3.198).
Such PDEs belong to the class of pseudo-parabolic equations that may enjoy some
properties of standard parabolic flows. Examples include the linear analogy
u
t
− u
xxt
= u
xx
,
and the regularized PBBM equation (see Example 4.45)
u
t
− u
xxt
= uu
x
+ εu
xx
(ε > 0).
The advantage of such pseudo-parabolic PDEs is that applying the inverse operator
(I − D
2
x
)
−1
with positive integrable kernel yields non-local equations with compact
operators, which can be studied by nonlinear integral operators theory.
Standard theory does not apply to quasilinear PDEs, such as (3.198), which, in
addition, are degenerate at the singular set {u = 0}. Mathematical theory of such de-
generate PDEs with nonnegative solutions (or, possibly, solutions of changing sign)
is unavailable. As usual, we will use solutions on invariant subspaces for formal de-
tecting some evolution singularities.
Example 3.39 (Quenching, interfaces, and the Cauchy problem) Consider the
PDE (3.198) for n = 1 with a constant absorption,
u
t
= F[u] ≡ (uu
t
)
xx
− 1,
bearing in mind the phenomenon of finite-time extinction. F is associated with sub-
space (module) W
2
= L{1, x
2
}, so there exist exact solutions
u(x , t) = C
1
(t) + C
2
(t)x
2
,
C
1
= 2(C
1
C
2
)
− 1,
C
2
= 12C
2
C
2
.
We take, e.g., C
2
=
1
12
(any constantC
2
fits), and the first equation is then integrated,
u(x , t) =
6
5
(T − t) +
1
12
x
2
, (3.200)
where T > 0isthefinite quenching time. For t < T , the solution is strictly positive.
At t = T
−
, the solution touches the singularity level {u = 0}. We readily derive the
asymptotic extinction behavior as t → T ,
u(x , t) = (T − t)g
0
(ξ), ξ =
x
√
T −t
, where g
0
(ξ) =
6
5
+
1
12
ξ
2
. (3.201)
Hence, (3.201) belongs to the class of self-similar solutions u
s
(x , t) = (T − t)g(ξ),
where g (and g
0
) solves the following third-order ODE:
g
1
2
g
ξ − g
−
1
2
g
ξ + g − 1 = 0.
These solutions on W
2
explicitly describe the quenching behavior for this degen-
erate quasilinear PDE. A rigorous stability analysis of such quenching is
OPEN (it
is likely that it is not generic or robust at all). In the rescaled sense, this assumes,
introducing the rescaled function u(x, t) = (T −t)v(ξ, τ ), with τ =−ln(T −t), to
study the third-order rescaled PDE
v
τ
=
v
1
2
v
ξ
ξ −v + v
τ
ξξ
−
1
2
v
ξ
ξ +v − 1.
© 2007 by Taylor & Francis Group, LLC

158 Exact Solutions and Invariant Subspaces
This means, passing to the limit τ →∞, that, for a class of positive, symmetric, and,
say, convex initial data (recall the parabolic shapes,
6
5
T +
1
12
x
2
, of initial functions
in W
2
), the convergence takes place,
v(ξ,τ) → g
0
(ξ) as τ →∞ (i.e., as t → T
−
).
Interface propagation. For t > T , the problem admits a suitable setting in the
class of nonnegative solutions in an FBP framework. It follows from (3.200) that the
right-hand interface is located at
s(t) = 6
2
5
√
t − T for t > T .
For such solutions u
x
=
x
6
, so that, at u = 0 in (3.200), −
6
5
(t − T ) + 3(u
x
)
2
= 0.
Plugging this into the expression for s
yields the dynamic interface equation
s
=
6
√
10
1
√
t−T
≡
6
5u
x
at x = s(t). (3.202)
On the Cauchy problem: oscillatory and non-oscillatory patterns. Let us for-
mally detect the maximal regularity that can be attributed to the CP. To keep pseudo-
parabolicity and extinction properties, consider the signed equation for n = 1,
u
t
= (|u|u
t
)
xx
− signu. (3.203)
Substituting the TWs u(x, t) = f (y), with y = x − λt, yields the ODE −λ f
=
−λ(| f | f
)
− sign f. Studying the right-hand interface, and hence, using the reflec-
tion y → −y, we keep the leading two terms on the right-hand side,
λ(| f |f
)
− sign f = 0fory > 0, f (0) = 0. (3.204)
It follows that the behavior near the interface at y = 0isgivenby
f (y) = y
3
2
ϕ(s), with s = ln y,
where the oscillatory component ϕ(s) solves a third-order ODE. Such ODEs were
studied earlier in the TFE applications; see (3.166). Therefore, ϕ(s) is oscillatory
and changes sign for λ<0, and is non-oscillatory for λ>0. Such TW properties
are expected to make sense in the CP for (3.203). Its well-posedness is
OPEN.Note
that the same ODE (3.204) occurs for the signed nonlinear dispersion equation (see
Section 4.3 for details)
u
t
=±(|u|u
x
)
xx
− signu.
Secondly, for the original model (3.198) without strong absorption
u
t
=
|u|
n
u
t
xx
(n > 0),
the same TW analysis leads to the ODE (| f |
n
f
)
= f for y > 0, which always
admits the strictly positive (non-oscillatory) solution
f (y) =
n
2
2(n+2)
1
n
y
2
n
.
The regularity at the interface y = 0 increases without bound as n → 0
+
when
approaching the linear PDE.
© 2007 by Taylor & Francis Group, LLC

3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 159
Example 3.40 (Sixth-order PDE) Considera higher-orderpseudo-parabolicmodel,
such as
u
t
=
|u|
n
u
t
xxxxxx
. (3.205)
The TW profiles satisfy
(| f |
n
f
)
(5)
= f for y > 0, f (0) = 0.
For n ∈ (0, 1), there exists a strictly positive, non-oscillatory solution f (y) = c
0
y
6
n
,
where c
0
> 0 is a constant.
Example 3.41 (Single point blow-up) Consider next a pseudo-parabolic PDE with
an extra reaction term,
v
t
=
v
n
v
t
xx
+ v
2−n
2
, (3.206)
where, for n < 0, the source term is superlinear for v 1andmaycreatefinite-time
blow-up singularities. In order to deal with polynomial subspaces, set
v = u
µ
, with µ =
2
n
,
to get a cubic PDE of the form
u
t
= u
2
u
xxt
+ 2(µ + 1)uu
x
u
xt
+(µ + 1)
uu
xx
+ µ(u
x
)
2
u
t
+
1
µ
≡ F
3
[u] +
1
µ
.
(3.207)
Proposition 3.42 F
3
in
(3.207)
admits subspace
W
3
= L{1, x , x
2
}
iff
2µ
2
+ 7µ + 6 = 0 ⇐⇒ µ =−2,
or
µ =−
3
2
. (3.208)
Substituting into (3.207) u(x, t) = C
1
(t) +C
2
(t)x
2
yields that (3.208) annuls the
term on L{x
4
}.Thisgives
C
1
= 2(µ + 1)C
1
C
2
C
1
+ 2C
2
1
C
2
+
1
µ
,
C
2
= 2(µ + 3)C
1
C
2
C
2
+ 2(µ + 1)(2µ + 1)C
2
2
C
1
.
(3.209)
Thus, such solutions exist in two cases, where (3.206) is
v
t
=
v
−1
v
t
xx
+ v
3
2
for n =−1 (µ =−1);
v
t
=
v
−
4
3
v
t
xx
+ v
5
3
for n =−
4
3
(µ =−
3
2
).
For both PDEs, we detect from the DS (3.209) the generic (on W
3
) extinction behav-
ior for the function u(x, t), which is equivalent to blow-up for v(x, t). For smooth
bounded orbits of the DS, the first equation near extinction time T reads C
1
=
−
1
|µ|
+ ... , and the second equation yields C
2
(t) → d > 0, from which we ob-
tain the asymptotic pattern
u(x , t) = (T − t)
1
|µ|
+ dx
2
+ ... = (T − t)
1
|µ|
+ d ξ
2
+ ... as t → T
−
,
with the spatial rescaled variable ξ = x/
√
T − t. In terms of the original solution
v = u
2/n
of the initial PDE (3.206), this yields the following single point blow-up
behavior as t → T
−
for n =−1orn =−
4
3
:
w(ξ, τ) ≡ (T − t)
−
2
n
v(x , t) → g(ξ) ≡
1
|µ|
+ d ξ
2
2
n
(3.210)
© 2007 by Taylor & Francis Group, LLC

160 Exact Solutions and Invariant Subspaces
uniformly in ξ ∈ IR . As happened before to other blow-up models, such behavior
corresponds to a delicate case of a singular perturbed first-order Hamilton–Jacobi
equation. To reveal this singular limit, we write down the perturbed PDE for the
rescaled function w(ξ, τ) as follows:
w
τ
=−
1
2
w
ξ
ξ +
2
n
w + w
2−n
2
+ e
−τ
w
2
w
τ
−
2
n
w +
1
2
w
ξ
ξ
ξξ
. (3.211)
This is an exponentialperturbationof theHamilton–Jacobiequationw
τ
=−
1
2
w
ξ
ξ+
2
n
w + w
2−n
2
that possesses g(ξ) in (3.210) as a stationary solution. There is a large
amount of mathematicalliterature devoted to infinite-dimensionalsingular perturbed
DSs associated with blow-upand extinctionphenomenafor reaction-diffusionPDEs;
see [245, Ch. 5, 9–11]. These well-developed techniques do not apply to the per-
turbed PDE (3.211) for which establishing uniform boundedness and compactness
of the rescaled orbits in suitable metrics are also
OPEN.
Remarks and comments on the literature
In many occasions we put references concerning specific models, equations, and applications
alongside corresponding examples. Other references are given below.
§3.1.Earlier references on the derivation of the fourth-order TFE can be found in [263, 531],
where the first analysis of some self-similar solutions was performed for n = 1. Source-
type (ZKB) similarity solutions for arbitrary n were studied in [48] for N = 1 and [185]
for the equation in IR
N
. More information on similarity and other solutions can be found
in [46, 45, 78]; see also a discussion of the TFE in the afterword of Barenblatt [25]. Thin
film equations admit nonnegative solutions constructed by special parabolic approximations
of the degenerate nonlinear coefficients; see the pioneering paper [44], various extensions in
[264, 167, 376, 576], and the references therein. For estimates of not necessarily nonnegative
solutions in IR
N
, see [265] and the bibliography therein.
The family (3.7) of generalized TFEs was studied in [345], where further references and
physical motivation can be found. The equation (3.3) was derived and studied in [155]; see
[529] for a parallel development. Equation (3.8) with m = n = 3 has been used to describe
bubble motion in a capillary tube and the Rayleigh–Taylor instability in a thin film [279]. For
more information on the modeling and physics of thin liquid films, we refer to survey papers
[430, 451, 34]; see also references in [431]. See [53]–[55], [293] for more general PDEs, such
as (3.9). The doubly nonlinear equation
u
t
=−(u
n
|u
xxx
|
l
u
xxx
)
x
describes, for n = l +3, the surface tension-driven spreading of a power-law fluid and, for n =
1, a power-law fluidinaHele–Shaw cell; see [345], survey [451], and mathematics in [14].
The exponent l is determined by rheological characteristics of the liquid, so l = 0 corresponds
to a Newtonian liquid, while l = 0 appears for “power-law” (Ostwald–de Waele) liquids,
called shear-thinning if l > 0. For such liquids, a typical sample relation of the viscosity η
and the shear rate ˙γ is of the form η ∼˙γ
−l/(l+1)
.
Concerning the Benney equation (3.10) [39] and models of falling liquid films, see [452].
Notice earlier experimental findings of P.L. and S.P. Kapitza [315] in 1949 related to travel-
ing waves in such models. On Marangoni instability in thin film models (3.12), see [450].
Semilinear Cahn–Hilliard equations were introduced in [92]; see [438] and references therein.
© 2007 by Taylor & Francis Group, LLC

3 Thin Film, Kuramoto-Sivashinsky, and Magma Models 161
The sixth-order thin film equation (3.13) was introduced in [338, 339] in the case of n = 3,
and describes the spreading of a thin viscous fluid under the driving force of an elastica or
light plate. In addition, [338, 339] treat a more general form of this equation (now allowing
for a reaction at the usual solid interface), which is shown to arise in the industrial application
of the isolation oxidation of silicon. Analysis for a finite length elastica or plate is given in
[176], whilst a numerical scheme with subsequent parameter investigation of the more general
system is derived in [177]. Delicate aspects of unusual similarity solutions and asymptotics
can be found in [189]. Some particular features of the 2mth-order PDEs (3.16) were already
considered in [531], where the n-small and waiting-time solutions were noted. Doubly non-
linear equations, such as (3.22), which are relevant to capillary driven flows of thin film of
power-law fluids, were derived in [345, 513]. Extra absorption terms in TFEs (see (3.25)) or
the source terms are to model effects of evaporation (certain permeability of the surface may
also be taken into account) or condensation, [451]. Actually, evaporation phenomena of thin
films are well known for binary solutions (see references in [261]), which probably hardly
apply to thin films on flat surfaces. The Florin problem for the fourth-order TFE with the con-
stant non-zero angle u
x
= C at the interfaces, which is a lubrication model related to Darcy
flow in a Hele–Shaw cell, was studied in [454].
Discussing other related higher-order models, note that similarity solutions of the equation
with a monotone operator in H
−2
,
u
t
=−(|u|
m−1
u)
xxxx
,
were studied in [47], where, for m > 1, solutions were proved to be compactly supported and
oscillatory (changing sign) near the interfaces. Other lubrication-type PDEs
u
t
=−(u
n
u
xx
)
xx
and u
t
=−|u|
n
u
xxxx
(n < 0)
were introduced in [52]. The fourth-order parabolic equation
u
t
=−(u(ln u)
xx
)
xx
arises in the context of interface fluctuations in spin systems and semiconductor theory; see
mathematics and references in [64, 307]. The sixth-order PDEs
u
t
= (u
n
|u
xxxxx
|
m−1
u
xxxxx
)
x
and u
t
={u[
1
u
(u(ln u)
xx
)
xx
+
1
2
((lnu)
xx
)
2
]
x
}
x
are obtained, respectively, for power-law fluids spreading on a horizontal substrate [345] and
as a generalized quantum drift-diffusion model for semiconductors, [146, 307]. Critical expo-
nents and asymptotic and singularity phenomena for the eighth-order TFE
u
t
=−(u
n
u
xxxxxxx
)
x
are discussed in [189]. Various aspects concerning oscillatory solutions of the Cauchy problem
for TFEs can be found in [174, 175], where further references are given.
Higher-order parabolic PDEs also occur in curve shortening flows for curves in two di-
mensions, whose normal velocity V
n
is given by the Laplacian of its curvature; see [91]. The
corresponding equation V
n
≡ N
t
=−κ
ss
(s is the arclength) for curves y = u(x, t) on the
{x, y}-plane, can be written as (see [82])
u
t
=−
1
√
1+(u
x
)
2
u
xx
√
1+(u
x
)
2
x
x
.
The hierarchy of such models of arbitrary order (the third-order PDE belongs to the KdV fam-
ily) goes back to Mullins [428], who proposed classical theory of thermal grooving. Arbitrary
order integrable models V
n
= D
l
s
κ were analyzed in [82]. Other fourth-order parabolic PDEs
© 2007 by Taylor & Francis Group, LLC

162 Exact Solutions and Invariant Subspaces
appear [116] in blow-up analysis of the curve evolution of an immersed plane curve according
to the H
−1
gradient flow.
Exact solutions on invariant subspaces exist for some non-local parabolic equations related
to the b–l model of the propagation of turbulent bursts from a horizontally uniform layer (see
model statement in [26] and [25, p. 291]),
b
t
= l(t)b
3
2
− k
b
1
2
l
2
(t)
in IR
N
× IR
+
,
where k > 0isafixed constant, and l(t)>0 is the measure of the support of a nonnegative
bounded solution, l(t ) = meas supp b(·, t ) ≡ meas {x ∈ IR
N
: b(x, t )>0}. Aclassof
such equations with invariant subspaces was studied in [224]. Another invariant subspace is
available in the b–ε model of turbulence motion based on the ideas of A.N. Kolmogorov and
L. Prandtl:
b
t
= α(
b
2
ε
b
x
)
x
− ε,
ε
t
= β(
b
2
ε
ε
x
)
x
− γ
ε
2
b
,
where α, β,andγ are positive constants. Here b(x, t ) ≥ 0 denotes the turbulent energy
density, and ε(x, t)≥ 0 is the dissipation rate of turbulent energy. See [27, 26] and [56] for
physical justification and further references. For α = β, the finite-time extinction behavior
can happen on a polynomial subspace invariant under quadratic operators [224].
§3.2.Some details concerning spectra, compact resolvent, and sectorial properties of linear
operators like (3.52) can be found in [163]. Note that, as a rule, rescaled higher-order parabolic
PDEs contain non-symmetric and non-potential operators. The spectral theory in [163, 87] of
similar (but not precisely the same) operators appears in the study of asymptotic blow-up and
global behavior for semilinear 2mth-order parabolic equations
u
t
=−(−)
m
u ±|u|
p−1
u.
[424]. On oscillatory and other features of the CP for the fourth-order TFEs, see [174].
§ 3.4, 3.5. Proposition 3.7 is taken from [343] (transformation (3.60) was firstusedin[531]
for formal perturbation analysis for small n), where Proposition 3.29 was used for m = 2.
Various results on the FBP and the CP for the sixth-order TFEs are available in [175].
§ 3.6, 3.7. Basic properties of oscillatory solutions of the CP for TFEs of various orders with
more detailed description are given in [174, 175]; see also [227].
§3.8.The KS-type equations are used as a description of the fluctuations of the position of
flame front [202, 203], the motion of fluid on a vertical wall, and chemical reactions with
spatially uniform oscillations on a homogeneous medium. Similar models also occur in solid-
ification, [201]; see survey [411]. The mKS equation (3.172) is a model for the dynamics of a
hyper-cooled melt [514]. A more general class of such models was introduced and discussed
in [289]. Blow-up in the mKS equations was studied in [50].
§3.9.In the magma equation (3.199), u(x, t) ≥ 0 measures the volume fraction of liquid
phase [519]. The exponents n and l describe permeability and effective viscosity characteriz-
ing the rate of matrix compaction and distension on u. Similar pseudo-parabolic PDEs occur
in modeling of thin film flows for poroviscous droplets over a planar substrate [347].
Open problems
• These are formulated throughout the chapter in Section 3.2, Examples 3.8–3.10,
3.14, 3.17, Remark 3.28, Section 3.7, and Examples 3.36, 3.37, 3.39, and 3.41.
© 2007 by Taylor & Francis Group, LLC
§3.3.The original von Mises transformation (see Example 3.10) was introduced in 1927,
