Galaktionov V.A., Svirshchevskii S.R. Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics

Подождите немного. Документ загружается.

4 Korteweg-de Vries and Harry Dym Models 173

ularity and the solutions are always, at least, continuous and sufﬁciently smooth at

any regular point (cf. TFEs in Chapter 3).

For ﬁrst-orderPDEs that are known as conservation laws, such as the Euler equa-

tion originated from gas-dynamics

+ uu

= 0, (4.34)

discontinuous shocks have been recognized for more than a century. General theory

of discontinuous entropy solutions of one-dimensional PDEs like (4.34) is due to

Oleinik [441] developed in the 1950s; see Smoller [530, Part III] for names, results,

references and amazing history of conservation laws. Among other important prop-

erties, one of the key features is that, in the most general case, the entropy solutions

are obtained by regularization, i.e., at the limit as ε → 0

of the family of smooth

solutions {u

} of uniformly parabolic Burgers’ equation

+ uu

= εu

. (4.35)

The ﬁrst such ideas were due to Hopf (1950) and Burgers (1948).

Discontinuous solutions can occur for higher-orderPDEs from compacton theory,

though a suitable entropy-like approach is extremely difﬁcult to develop along the

lines of that for conservation laws. This is a principal

OPEN PROBLEM. Due to highly

oscillatory properties of solutions (see oscillatory asymptotics of the Airy function

and other fundamental kernels in the next section), formation of shock waves cannot

be described by exact solutions on simple invariant subspaces. We brieﬂydiscuss

third or ﬁfth-order PDEs with quadratic leading-order operators

= (uu

)

, or u

+ (uu

)

xxxx

= 0. (4.36)

Consider two basic Riemann’s problems for PDEs (4.36). First, this is the formation

of the stationary shock wave S

−

(x ) =−sign x (it is entropy for (4.34)),

−

(x ) =



1forx < 0,

−1forx > 0,

(4.37)

from smooth solutions in ﬁnite time, as t → T

−

. This phenomenon is described by

the similarity solution

(x , t) = g(z), where z =

(T −t )

1/3

, or z =

(T −t )

1/5

, (4.38)

and g solves the following ODEs obtained on substitution into (4.36):

(gg



)





z, or (gg



)

(4)

=−



z, with f (±∞) =∓1. (4.39)

For these higher-orderODEs, existenceand uniquenessproblems are not easily stud-

ied analytically and are

OPEN. Numerically, we have evidence that, in each case,

such a smooth odd proﬁle g is unique. Figure 4.6 shows the proﬁles G = g

(z) for

z < 0. For z > 0, g(z) is extended anti-symmetrically to get the odd function. Such

similarity proﬁles g(z) describe formation of shocks, i.e.,

(x , t) → S

−

(x ) as t → T

−

for any x ∈ IR , uniformly in IR \ (δ, δ), with a δ>0small,andinL

loc

(IR ).Itis

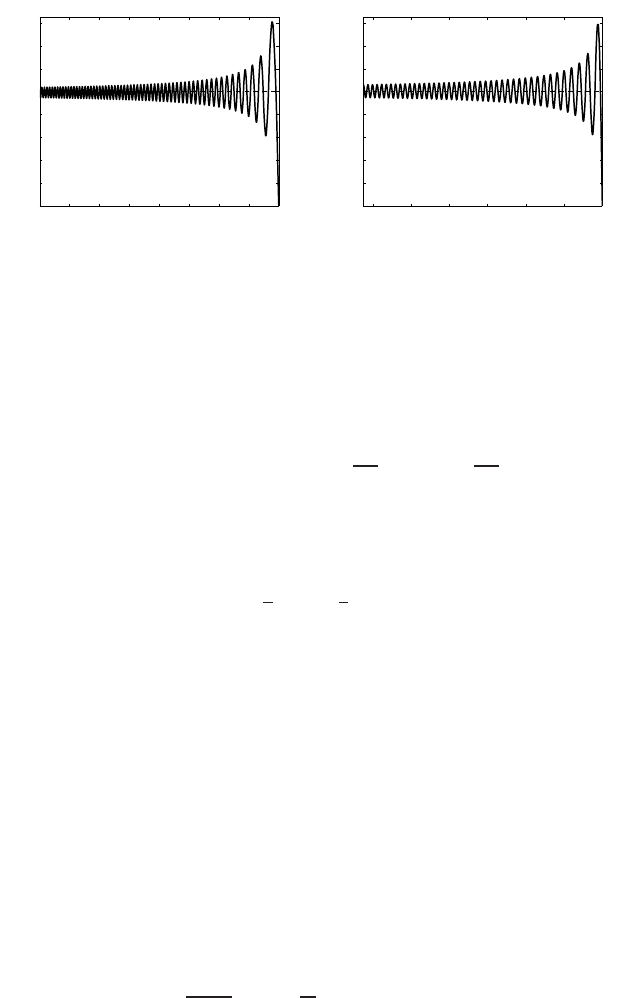
174 Exact Solutions and Invariant Subspaces

 80  70  60  50  40  30  20  10 0

0.2

0.4

0.6

0.8

1.2

1.4

1.6

G=g

(z)

Gradient blow up to S



(x) and collapse of S

(x) for u

=(uu

)

(a) third-order

 120  100  80  60  40  20 0

0.2

0.4

0.6

0.8

1.2

1.4

1.6

G=g

(z)

Gradient blow up to S



(x) and collapse of S

(x) for u

+(uu

)

xxxx

(b) ﬁfth-order

Figure 4.6 The shock wave similarity proﬁle g(z) satisfying ODEs (4.39).

curious that, for the third-order case, in view of asymptotics of Airy functions given

in (4.139), the total variation of u

(x , t) for any t < T is inﬁnite. The same is true

for the ﬁfth-order case. This strongly differs from the ﬁnite variation approach for

ﬁrst-order PDEs (4.34) that is key in scalar conservation laws theory, [441].

Using the reﬂection symmetry u → −u, t → −t of PDEs (4.36) implies that the

same similarity solutions deﬁned for t > 0,

(x , t) = g(z), with z =

1/3

, or z =

1/5

, (4.40)

describe the collapse of the non-entropy shock S

(x ) = sign x, posed as initial data.

Then (4.40) plays the role of the rarefaction wave that, for the conservation law

(4.34), has the simpler similarity piece-wise continuous form

(x , t) = g(

) =



−1forx < −t,

for |x | < t,

1forx > t.

This means that S

(x ) is not an entropy shock. The same classiﬁcation of stationary

shocks S

(x ) as solutions of two Riemann’s problems applies to similar PDEs of

arbitrary (2m+1)th order,

= (−1)

m+1

(uu

) for m = 1, 2, ... . (4.41)

For instance, consider parabolic ODE ε-approximations {u

(x )} of the stationary

shock S

−

(x ) for (4.41),

(−1)

m+1

(uu

) + (−1)

εD

2m+2

u = 0.

Integrating 2m times with zero constants, we obtain the problem

= εu

, with u(±∞) =∓1.

This is precisely the correct entropy approximation (4.35) (with u

= 0) for the

ﬁrst-order conservation law, and the approximating sequence is as follows:

(x ) =

1−e

x/ε

1+e

x/ε

= tanh

2ε

→ S

−

(x ) as ε → 0

with pointwise and L

(IR ) convergence. Notice that, unlike the above similarity so-

lutions, such approximating proﬁles are strictly monotone and are not oscillatory

4 Korteweg-de Vries and Harry Dym Models 175

about ∓1asx →±∞(this is related to the chosen special type of parabolic approx-

imation). Therefore, for the corresponding (2m+1)th-order ODEs, the shock S

−

(x )

is admissible in Gel’fand’s sense (1963), or G-admissible, while S

(x ) is not.

Later on, using invariant subspace techniquesfor odd-orderPDEs, we will not pay

the attention to the possible appearance of proper entropy shocks as solutions that

are obtained via regular parabolic approximations. As we have seen, other similarity

solutions are needed to revealing such singular phenomena.

4.2.3 On interface equations for compactons

Due to the degeneracy of the higher-order operators at u = 0, compacton (4.21) has

ﬁnite interfaces. Similar to parabolic problems for TFEs (cf. Example 3.10), these

explicit solutions help to identify the interface equation.

Example 4.8 (Interface equation) Let us begin with a slightly rescaled RH equa-

tion (4.14),

= (u

)

xxx

+ 4(u

)

≡



)

+ 4 u



. (4.42)

Then (4.12) holds and the explicit traveling wave solution is obtained,

u(x , t) = f (y) ≡−

sin

(

), where y = x − λt, (4.43)

where, in order to have a nonnegative solution, it is assumed that λ<0, i.e., the TW

moves to the left. The compacton consists of the single hump for y ∈ (0, 2π).For

the sin

-wave in (4.43), the left-hand interface is ﬁxed at the origin y = 0. We then

naturally pose the free-boundary condition of a zero contact angle type from thin

ﬁlm theory (Section 3.1),

u = u

= 0 at the interface x = s(t). (4.44)

For regular solutions, (4.44) implies the zero-ﬂux condition for PDE (4.42), i.e.,

)

+ 4u

= 0atx = s(t).

In a standard manner, a formal dynamic interface equation is derived by differentiat-

ing u(s(t), t) = 0 and using the PDE (4.42), so that



= S[u] ≡−

=−6u

at x = s(t). (4.45)

As usual, this is not an independent free-boundary condition, and is just a mani-

festation of the regularity, so (4.45) is true for any smooth solutions (not necessarily

with the zero contact angle condition, i.e., remains valid for Stefan–Florin FBPs with

= S[u] = 0).

Let us detect other conditions for such sufﬁciently regular solutions. Now using

either the explicit solution (4.43) or the ODE for f (this is necessary to do if explicit

solutions are not available), that is

−λf



= ( f

)



+ 4( f

)



, (4.46)

we obtain the following expansion for small y > 0:

u(x , t) = f (y) = By

+ Cy

+ ... , (4.47)

176 Exact Solutions and Invariant Subspaces

with B =

(0, t) and C =

xxxx

(0, t).Theﬁrst coefﬁcient is then given by

B =−

λ = 6u

coinciding with (4.45). Recall that s



= λ for the TWs. The

second coefﬁcient satisﬁes

−λC = 60BC + 4B

which yields the desired second interface equation



= S[u] ≡−30u

−

xxxx

)

at x = s(t). (4.48)

Using (4.45) reduces the dynamic condition (4.48) to a “stationary” higher-order

Neumann-type condition

=−u

xxxx

at x = s(t).

These are interface free-boundary conditions which should be satisﬁed in order to

generate a (unique) sufﬁciently regular solution. A rigorous justiﬁcation needs the

von Mises transformation for the new function u = v

with the transversal interface

slope, v

= 0atx = s(t). This leads to a third-order degenerate PDE for X =

X (v, t) with the boundarycondition (4.45) at the origin v = 0, whichis necessaryfor

the correct functionalsetting of the corresponding degenerateoperator. This problem

is locally well-posed, provided that v

= 0atv = 0. Some features are similar to

those in parabolic Example 3.10, though the proof is not easy. There are several

OPEN PROBLEMS in such an approach.

4.2.4 On proper solutions by parabolic approximations

Compactons initiate further intriguing aspects of nonlinear PDE theory. Here, we

face another principal questionwhich remains

OPEN for such weak solutions of wide

classes of degenerate nonlinear dispersion models. Namely, it is key to identify the

problem for solutions (4.43). If these are solutions of the Cauchy problem (so that

the free-boundary conditions do not need to be posed explicitly), it is expected that

(4.43) can be obtained by smooth approximations,

u(x , t) = lim

ε→0

(x , t), (4.49)

via, say, regular analytic parabolic ﬂows. For instance, using the family {u

,ε>0}

of analytic solutions of the uniformly parabolic PDEs

=−εu

xxxx

+ (u

)

xxx

+ 4(u

)

, (4.50)

with the same compactly supported initial data u

(x ). On the other hand, a sixth-

order regularization

= εu

xxxxxx

+ (u

)

xxx

+ 4(u

)

(4.51)

may be applied. Do both ε-approximations lead to the same solution deﬁned by

(4.49)? [See a partial answer for TWs below.] For some good solutions of (4.50),

e.g., those having a ﬁnite number of zeros that are uniformly transversal for all small

ε>0, the passage ε → 0 is rather straightforward (each isolated transversal zero

is localized, stable in ε and hence, cannot spoil the limit ε → 0). The principal

4 Korteweg-de Vries and Harry Dym Models 177

question is how to deal with generic highly oscillatory solutions u

(x , t). This leads

to the general problem of multiple zeros structure for solutions of the degenerate

PDE (4.42) and other models. This is a part of the Sturmian zero set analysis,which

was initiated by Sturm in 1836 [538] for the 1D second-order parabolic equations

(e.g., for the heat equation); see history, modern developments, and many applica-

tions in [226,Ch. 1]. Notice that, for the semilinear KdV equation (4.1), the parabolic

regularization, as in (4.50), has been recognized since the 1960s (Temam) to be an

effective approach to nonlinear PDEs; see [396, Ch. 3].

Passing to the limit ε → 0

in the regularized PDEs (4.50), (4.51) and similar

equations represent a hard

OPEN PROBLEM. Existence of a (unique) solution of the

CP now becomes a delicate ε-asymptotic problem. This is a common unavoidable

feature of many higher-order nonlinear degenerate and singular PDEs considered in

this and other chapters. As an illustration, consider this asymptotic problem for the

PDE (4.50) understood in the weak form



χ dx −



=−ε



xxxx



)

− 4



)

, (4.52)

where χ ∈ C

∞

is a test (cut-off) function. In general, the weak form of equations

is not necessarily the best way for proper setting of many nonlinear problems. For

instance, the weak approach fails for not fully divergent operators as for the THEs

in Chapter 3 (though they are divergent in (4.50)). In these cases, we need to study

directly the limit of the smooth family {u

} as ε → 0, which givesa number of OPEN

PROBLEMS

, especially for higher-order quasilinear nonlinear dispersion (or elliptic)

operators; see Remarks for further comments.

Passage to the limit ε → 0 in the integral identity (4.52) assumes the study of a

couple of singular integrals. For compactly supported u

(x ) given by (4.43),

(x ) =−

sin

(

) for x ∈ [0, 2π ], (4.53)

there are far ﬁeld integralsfor |x|1, whichare extremelysmall via the exponential

tails of the fundamental solution of the parabolic operator

∂

∂t

+ ε D

(x , t) ∼ exp



a|x |

/(εt)



with some complex constant a such that Rea < 0. Other harder integrals describe

the behavior in domains with the resonance interaction between two higher-order

terms in (4.50). For x ≈ 0, we use scaling

u(x , t) = ε

v(y,τ), y =

1/3

,τ=

1/3

where v(y,τ)now solves the uniformly parabolic equation

=−v

yyyy

+ (v

)

yyy

+ 4ε

)

. (4.54)

The initial function is calculated from (4.53) as follows:

(y) ≡−

−

sin





→−

as y → 0

. (4.55)

Since τ →+∞as ε → 0

,thisﬁxes the asymptotic problem for the parabolic

PDE (4.54) with O(y

) initial data on bounded intervals. It is not very difﬁcult to

178 Exact Solutions and Invariant Subspaces

justify that, by parabolic theory, this CP for (4.54) is well-posed and admits a unique

global solution. This is the principal fact testifying that the sequence {u

} cannot

have non-small, O(1)-oscillations as ε → 0. In this case, the limit (4.49) gives a

unique (proper) solution of the Cauchy problem.

Let us demonstrate that the O(y

) behavior in (4.55) does not generate large, un-

bounded asymptotics as τ →+∞, which can affect the corresponding singular

integral in (4.52) and the limit (4.49). To this end, as a formal estimate, let us com-

pare v(x ,τ) with the standard similarity solution of (4.54) (without the last term

negligible for ε & 1)

∗

(y,τ)= τ

−

g(z), with z =

1/4

where g satisﬁes the ODE

−g



gz + (g

)



= 0, g(+∞) = 0.

Then g(z) ∼ e

4/3

, with Re a =−

−1/3

< 0, has exponential decay as z →+∞,

while for z &−1, it has a cubic growth of the form

g(z) ∼

120

(−z)

+ ... as z →−∞.

It then follows that such a nontrivial solution occurs from more singular initial data

∗

(y,τ)∼

as τ → 0

For O(y

) data, the asymptotic behavior is less singular and the inﬂuence in the

integral identity of such an internal layer near the origin is negligible as ε → 0.

This analysis indicates how ε-asymptotic theory penetrates into the existence and

uniqueness construction of proper solutions. For more general, non-inverse bell-

shaped initial data, we can have many internal singular layers (possibly an uncount-

able set?), which shouldbe takeninto account. In generalsettings, the passage ε → 0

is very difﬁcult and remains

OPEN for most regularized PDEs considered later on.

On the other hand, for TWs, this asymptotic analysis is not hard and deals with

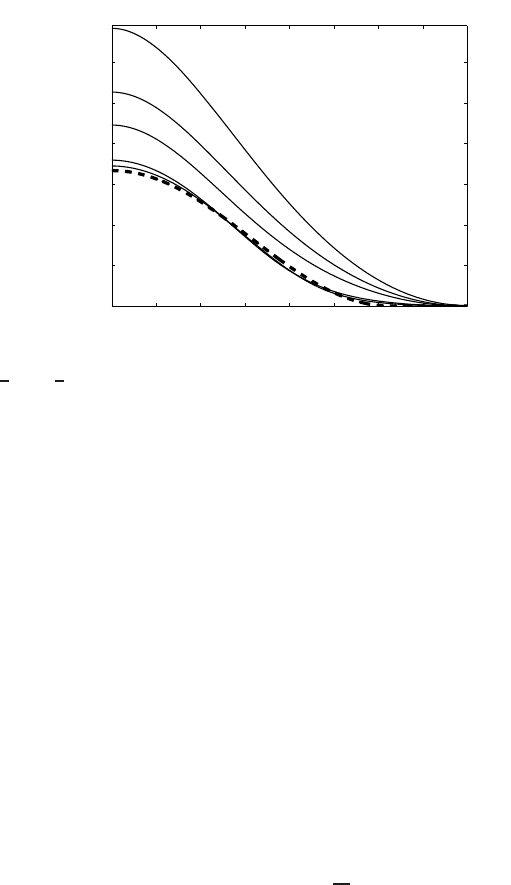
standardmatched asymptoticexpansions.Figure 4.7 shows the (non-monotone)con-

vergence as ε → 0 of the TW proﬁles satisfying the third-order ODE

−λf =−ε f



+ ( f

)



+ 4 f

. (4.56)

Returning to our particular ODE approach, in order to detect maximal regular-

ity solutions of the Cauchy problem that may be inherited from the analytic ε-

regularization, it follows that expansion (4.47) yields the most smooth solutions of

the ODE (4.46) at the interface point. This is easily proved for these second-order

equations. Therefore, we claim (which may be obvious) that compactons (4.43) are

smooth solutions of the Cauchy problem for (4.42) and can be obtained without a

priori speciﬁed free-boundary conditions. A rigorous proof is not easy. The dynamic

interface equation then follows from the PDE for X = X (v, t) as explained above.

4 Korteweg-de Vries and Harry Dym Models 179

0 0.5 1 1.5 2 2.5 3 3.5 4

0.1

0.2

0.3

0.4

0.5

0.6

f(y)

Figure 4.7 Convergence as ε → 0 of solutions of (4.56), with λ =−1, to the compacton

proﬁle

cos

(

); ε = 2, 1, 0.5, 0.05, 0.01, and 0.001 (the dashed line).

4.2.5 Local behavior near interfaces for the K (2, 2) equation

Consider the quadratic PDE, keeping the leading differential term,

= (u

)

xxx

in IR × IR

, (4.57)

with given compactly supported initial data u

.Letusﬁrst study the TW solutions

of the form (4.43) satisfying, after integrating once, a simple ODE

−λ f



= ( f

)



⇒ ( f

)



+ λ f = 0. (4.58)

Thesesecond-ordernonlinear Emden–Fowler-type equations,introducedand studied

by Emden (1907) [168] and Fowler (1914) [200], seem to be the most famous and

well-studied ODEs in the twentieth century. We use in (4.58) the following standard

change that follows from a group of scalings,

f (y) = y

ϕ(s), s = ln y,

where ϕ solves the autonomous ODE

(ϕ

)



+ 7(ϕ

)



+ 12ϕ

+ λϕ = 0inIR . (4.59)

For λ = 0, there exists the nontrivial constant proﬁle

ϕ(s) ≡ ϕ

=−

. (4.60)

For λ<0, this solution is positive and actually leads to the existence of the explicit

nonnegative compacton (4.43). For λ>0, (4.60) is negative and the ODE (4.58)

has the obvious negative solution that is obtained by reﬂection f → − f , λ → −λ.

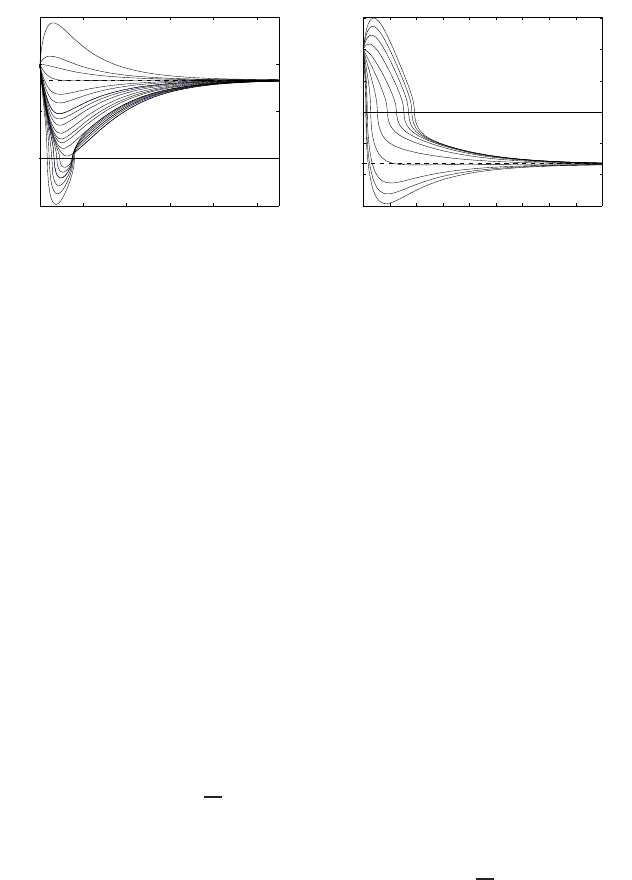
By linearization, the constant solution (4.60) of (4.59) turns out to be asymptotically

exponentially (O(e

−s

))stableass →+∞, and is unstable as s →−∞; see Figure

4.8. The phase-plane of (4.59) shows that no other changing sign solutions exist.

Thus the TW proﬁles are non-oscillatory for equation (4.57), though strictly positive

solutions close to interfaces are possible for λ<0 only.

180 Exact Solutions and Invariant Subspaces

0 1 2 3 4 5

 0.05

0.05

0.1

0.15

φ(s)

(a) λ =−1

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5

 0.15

 0.1

 0.05

0.05

0.1

0.15

φ(s)

(b) λ = 1

Figure 4.8 Asymptotic stability as s →+∞of the constant solution (4.60) of (4.59) for

λ =−1 (a) and λ = 1(b).

This is an ODE analysis of the local structure of movingTWs near interfaces. The

corresponding PDE result, after proving the existence of a proper solution u(x, t) of

the Cauchy problem for (4.57) (e.g., by the analytic regularization similar to that in

(4.50)), assumes establishing that the generic behavior at the interfaces is governed

by TWs. This is a difﬁcult

OPEN asymptotic problem that is typical for nonlinear

rescaled evolution PDEs, which is brieﬂy and formally discussed below. Namely,

given a proper solution u(x , t), the TW rescaling is performed as follows:

u(x , t) = v(y, t), y = x −λt,

so v solves the rescaled equation with the same ODE operator

= (v

)

yyy

+ λv

. (4.61)

For convenience, we study the behavior of the solution at the initial moment t = 0,

when the interface is at the origin, s(0) = 0, assuming that there exists the ﬁnite

speed of propagation λ = s



(0), i.e., the interface is a sufﬁciently smooth curve at

t = 0

−

. Proving such a regularity of interfaces is a hard OPEN PROBLEM.Then

the solution of (4.61) is rescaled according to the invariant group of scalings by

introducing the family of functions

(z,τ)=

v(µz,µτ), with parameter µ>0, (4.62)

where w

solves the same equation (4.61),

)

= [(w

)

]

zzz

+ λ(w

)

, with data w(z, 0) =

(µz). (4.63)

Then the limit µ → 0, describing, according to (4.62), the behavior of v(y, t) for

(y, t) ≈ (0, 0

−

), is equivalent to the passage to the limit τ →+∞, z →∞in

(4.63), i.e., studying the asymptotic behavior of its solutions. Here, convergence of

initial data w

(z, 0) as µ → 0 determines the necessary speed λ. Had we proved the

stabilizationto a nontrivialstationaryproﬁle,we wouldhaveestablishedthe behavior

of general solutions governedby the TWs given by (4.58).The equation (4.63) is not

a gradient system, i.e., it does not admit a Lyapunov function, so passing to the limit

as τ →+∞is an

OPEN PROBLEM.

4 Korteweg-de Vries and Harry Dym Models 181

4.2.6 The signed K (2, 2) equation: TWs and oscillatory solutions

We now explain the origin of the signed versions of nonlinear dispersion PDEs that

have already been used in Examples 4.6 and 4.7. Mathematically, this is related to

another approach for checking the evolution properties of the compacton (4.43) and

oscillatory properties of general solutions via the n-continuity (homotopy) construc-

tion. Instead of (4.57), consider the following PDE:

= (|u|u)

xxx

. (4.64)

For smooth nonnegative solutions, these PDEs coincide. The mathematical advan-

tage of (4.64) is that it admits a connection to the linear equation via the family on

the signed nonlinear dispersion equations

= (|u|

xxx

, with parameter n ≥ 0. (4.65)

Namely, at n = 0, the standard linear dispersion equation occurs,

= u

xxx

, (4.66)

exhibiting the well-known local and global evolution properties. Its fundamental so-

lution via Airy’s function is described in Example 4.27. We say that the PDEs (4.64)

and (4.66) belong to the same “homotopy class,” if wide sets of solutions (with, say,

stable transversal zeros only) of both can be continuously (in n) deformed to each

other. Therefore, both quadratic (4.64) and linear (4.66) equations should exhibit

similar local oscillatory properties of solutions.

This approach assumes the change of all the models,where in the PDEs and ODEs

we replace

→ |u|u,ϕ

→ |ϕ|ϕ, u

→ |u|

m−1

u, ... . (4.67)

For nonnegative compactons this does not matter. Using such monotone nonlinear-

ities in PDEs with nonlinear dispersion makes sense from a physical point of view,

[495]. Furthermore, for the parabolic equations of any order, including the TFEs in

Section 3.1, the only well-posedextensionof quadraticmodelsto solutionsof chang-

ing sign assumes transformations (4.67), so the correct setting of PDEs is

= (|u|u)

, u

=−(|u|u)

xxxxx

, u

= (|u|u)

xxxxxx

, etc.

Indeed, equations with non-monotone nonlinearities, such as (cf. (4.57))

= (u

)

, or u

=−(u

)

xxxx

are backward parabolic in the negativity domain {u < 0} and are not well-posed.

This motivates introducing the signed K (m, n) (sK (m, n)) equation

= (|u|

n−1

xxx

+ (|u|

m−1

so that, for proper construction of solutions of the Cauchy problem, it is natural to

use a homotopy connection as n, m → 1(n → n + 1 later on for convenience) to

the linear PDE

= u

xxx

+ u

in IR × IR ,

with well-known evolution and oscillatory properties of solutions.

182 Exact Solutions and Invariant Subspaces

Traveling waves. Constructing TW solutions of (4.65) yields the second-order ODE

(| f |

f )



+ λ f = 0fory > 0, f (0) = 0, (4.68)

which is easy to study by setting F =|f |

f ,sothat



=−λ



−

n+1

F for y > 0, F(0) = 0.

Hence, the following behavior near interfaces occurs:

F(y) =±



−

λn

2(n+1)(n+2)



n+1

2(n+1)

for λ<0.

For λ>0, it follows that F(y) ≡ 0, meaning nonexistence of ﬁnite TW-interfaces.

In this case, the ODE (4.68) admits arbitrarily small periodic solutions f (y) in IR ,

which, formally, have interfaces at y =±∞and are not decaying as y →∞.

On regularization: convergence for the TWs. We will now slightly touch on the

regularization problem, and, following (4.50), consider the parabolic PDE

=−εu

xxxx



|u|



xxx

Unlike (4.68), the TWs now solve the third-order singular perturbed ODE

−ε f





| f |





+ λ f = 0. (4.69)

Rigorous principles of singular perturbation methods for differential equations were

established by Tikhonov in the 1940s and 50s. Boundary layer phenomena are ex-

plained in well-known monographs by Vasil’eva and Butuzov, O’Malley, Kevorkian

and Cole, Lomov, and others.

Let us brieﬂy comment on the passage to the limit ε → 0 in (4.69). To study the

behavior near the interface as y → 0

, the standard change in (4.68) is used,

f (y) = y

ϕ(s), s = ln y, where γ =

. (4.70)

Plugging (4.70) into (4.68) and denoting  =|ϕ|

ϕ gives

[] ≡ 



3n+4





2(n+1)(n+2)

 + λ







−

n+1

 = 0. (4.71)

Applying the same change (4.70) in (4.69) we obtain the non-autonomousODE



+ 3(γ − 1)ϕ



+ (3γ

− 6γ + 2)ϕ



+γ(γ − 1)(γ − 2)ϕ =

[|ϕ|

ϕ].

(4.72)

Introducing the new independent variable

s → s +

lnε, (4.73)

we get rid of the ε-dependence on the right-hand side of (4.72). The behavior as

ε → 0 can be studied by matching methods from ODE theory. It follows that, since

the right-hand side in (4.72) becomes unbounded as ε → 0, good solutions must

approach the generic behavior of the ODE (4.71), formally corresponding to ε = 0.

Similarly, for the sixth-order regularization as in (4.51),

= εu

xxxxxx

+ (|u|

xxx

⇒ ε f

(5)



| f |





+ λ f = 0.