Galaktionov V.A., Svirshchevskii S.R. Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics
Подождите немного. Документ загружается.

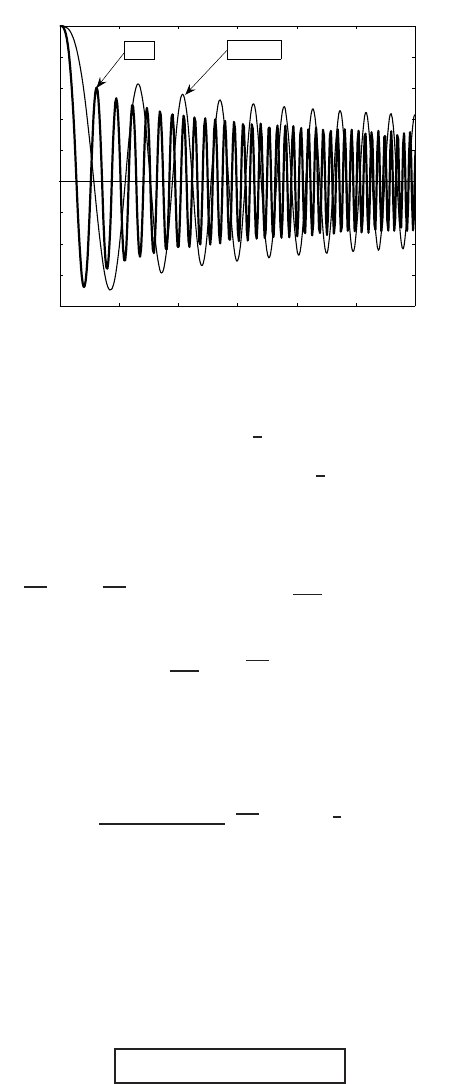
4 Korteweg-de Vries and Harry Dym Models 183
0 5 10 15 20 25 30
8
6
4
2
0
2
4
6
8
10
x 10
3
y
F(y)
n=0, Airy
n=1
Figure 4.9 Oscillatory behavior of solutions of (4.75) for large y > 0.
Then the oscillatory component ϕ solves the ODE (operator P
5
is as in (3.157))
P
5
[ϕ] ≡ ϕ
(5)
+ ... =
1
ε
e
5s
G
n
[|ϕ|
n
ϕ],
where, instead of (4.73), the translation s → s +
1
5
lnε applies. As ε → 0, the
convergence of bounded solutions to those of the ODE (4.71) is observed.
Solutions of changing sign. We describe these by constructingthe fundamentalsim-
ilarity solution of (4.65),
u(x , t) = t
−
1
n+3
f
x/t
1
n+3
⇒ (| f |
n
f )
+
1
n+3
fy = 0,
f = 1. (4.74)
Setting F =|f |
n
f yields
F
+
1
n+3
F
−
n
n+1
Fy = 0. (4.75)
For n = 0, this is the ODE problem for the Airy function Ai(y) as the kernel of
the fundamental solution of the linear operator in (4.66). For n > 0, assuming that
supp f = [y
0
, ∞) with some y
0
< 0, we have that, close to the finite left-hand
interface, as y → y
+
0
, the behavior is non-oscillatory (see Figure 3.5(a))
f (y) =
n
2
2(n+1)(n+2)(n+3)
1
n+1
(y − y
0
)
2
n
(1 + o(1)) .
For y 1, the behavior is different and f (y) does not have a finite interface. In Fig-
ure 4.9, we present a typical oscillatory behavior of the function F(y) = (| f |
n
f )(y)
for n = 1 to be compared with similar oscillations of the Airy function for n = 0.
4.3 Higher-order PDEs: interface equations and oscillatory solutions
Example 4.9 (Fifth-order PDE with nonlinear dispersion)Letus return to higher-
order degenerate PDEs, e.g.,
u
t
= (u
2
)
xxxxx
− 16(u
2
)
x
, (4.76)
© 2007 by Taylor & Francis Group, LLC

184 Exact Solutions and Invariant Subspaces
with the corresponding compacton
u(x , t) = f (y) ≡
λ
15
sin
2
1
2
y
, where y = x − λt. (4.77)
Here, λ>0, so that the TW moves to the right. These solutions satisfy the zero
contact angle condition (4.44) (notice that the condition u
xxx
= 0 holds for any even
f (y)), but the flux in not zero,
(u
2
)
xxxx
− 16u
2
= 6(u
xx
)
2
=
λ
15
at x = s(t). (4.78)
This is the first sign that compacton (4.77) is not a solution of the Cauchy problem.
For this smooth case, the dynamic interface equation is standard,
s
= S[u] ≡−
1
u
x
u
t
=−10u
xxxx
at x = s(t). (4.79)
We expect that the zero contact angle conditions (4.44) plus the Florin-type condi-
tion (4.78) (with λ = s
(t)) comprise a locally well-posed FBP for (4.76) generating
compactons with profiles (4.77). Hence, (4.79) will serve as a regularity solvability
criterion for the degenerate equation that is obtained via the von Mises transforma-
tion X = X (v, t) with u = v
2
. The problem of the well-posedness is OPEN.
4.3.1 On the Cauchy problem
Concerning the correct setting for the Cauchy problem, we continue to study the
ODE for TW profiles f ,
−λf
= ( f
2
)
(5)
− 16( f
2
)
. (4.80)
Let us showthat the quadraticbehavior as y → 0 as in (4.47), which remains true for
the current compactons, does not provide us with the maximal regularity exhibited
by the fifth-orderODE (4.80). To this end, consider the PDE with the leading higher-
order term only,
u
t
= (u
2
)
xxxxx
in IR × IR
+
. (4.81)
For TWs, the following ODE is obtained on integration:
−λf = ( f
2
)
(4)
for y > 0, f (0) = 0.
For λ<0, it admits the positive solution
f (y) =−
λ
1680
y
4
, (4.82)
which is smoother at the interface y = 0 than (4.77) for the FBP. Set
f (y) = y
4
ϕ(s), where s = ln y, (4.83)
where ϕ solves the following fourth-order autonomous ODE:
(ϕ
2
)
(4)
+ 26(ϕ
2
)
+ 251(ϕ
2
)
+ 1066(ϕ
2
)
+ 1680ϕ
2
+ λϕ = 0. (4.84)
For any λ = 0, there exists the constant equilibrium
ϕ(s) ≡−
λ
1680
, (4.85)
which for λ<0 is positive and leads to (4.82). In Figure 4.10 we show the behavior
of solutions of the ODE (4.84), so that (4.85) is asymptotically stable as s →+∞
© 2007 by Taylor & Francis Group, LLC

4 Korteweg-de Vries and Harry Dym Models 185
0 1 2 3 4 5 6 7
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
x 10
3
s
φ(s)
(a) λ =−1
0 1 2 3 4 5
7
6
5
4
3
2
1
0
x 10
4
s
φ(s)
(b) λ = 1
Figure 4.10 Non-oscillatory solutions of the ODE (4.84) for λ =−1 (a) and λ = 1(b).
for both λ>0andλ<0, with exponential convergence of the order O(e
−s
).The
lower left-hand corner of Figure 4.10(a) and the upper one in (b) show that the trivial
“equilibria” ϕ = 0 is highly unstable. Moreover, it seems that most of solutions of
(4.84) cannot change sign at all, unlike a number of other higher-order TFEs; cf.
Figure 3.8(a) and (b).
We expect that Figure 4.10 describes the generic non-oscillatory behavior near
interfaces of some classes of solutions of the PDEs, such as (4.76) in IR × IR ,i.e.,
moving TWs exhibit the following behavior of the maximal regularity:
f (y) = O(y
4
) as y → 0. (4.86)
Then the compactly supported function (4.77) is not a solution of the CP.
Example 4.10 (Signed fifth-order PDE: solutions of changing sign)Wenowde-
scribe the oscillatory interface behavior for the signed fifth-order nonlinear disper-
sion PDE with parameter n > 0,
u
t
= (|u|
n
u)
xxxxx
in IR × IR
+
. (4.87)
Oscillatory properties for the linear PDE. As usual, the advantage of the signed
PDE (unlike (4.81)) is that it admits the formal passage to the limit n → 0asa
connection to the linear dispersion equation
u
t
= u
xxxxx
in IR × IR
+
. (4.88)
Using TW solutions of (4.88) gives
−λf = f
(4)
,
so that setting f (y) = e
µy
yields µ
4
=−λ<0forλ>0. The generic decaying
behavior is oscillatory at the left-hand interface as y →−∞,
f (y) ∼ exp
λ
1
4
y
√
2
A cos
λ
1
4
y
√
2
+ B sin
λ
1
4
y
√
2
. (4.89)
For λ<0, the only decaying (integrable at y =−∞) solution is non-oscillatory,
f (y) ∼ exp
|λ|
1
4
y
as y →−∞.
In addition, there are bounded, non-integrable solutions.
© 2007 by Taylor & Francis Group, LLC

186 Exact Solutions and Invariant Subspaces
Alternatively, the fundamental solution of the corresponding linear operator
∂
∂t
−
D
5
x
in (4.88) is
b(x, t) = t
−
1
5
g(ξ), with ξ =
x
t
1/5
,
where g is a unique solution of the ODE problem
g
(5)
+
1
5
(gξ)
= 0inIR ,
g = 1. (4.90)
Then g(ξ ) ∼ e
aξ
5/4
as ξ →+∞, with a
4
=−
1
5
4
5
4
, so that the behavior is oscilla-
tory of the type
g(ξ) ∼ ξ
−
3
8
exp
−a
0
ξ
5
4
A sin
a
0
ξ
5
4
+ B cos
a
0
ξ
5
4
,
where a
0
=
4
5
√
2
5
−1/4
.Asξ →−∞, g(ξ) has stronger, not absolutely integrable
on (−∞, 0), oscillations,
g(ξ) ∼|ξ |
−
3
8
A sin
a
0
|ξ|
5
4
+ B cos
a
0
|ξ|
5
4
.
As a rule, in order to compare such oscillatory patterns with those for the quasilin-
ear model, we always formally mean that the left-hand interface for (4.88) is situated
at x =−∞, and not at a finite x, as for the degenerate PDE (4.87). Notice that,
for (4.88), there exists a single fundamental frequency of the linear periodic motion
and, most probably, this remains valid for (4.87) for small n > 0. In other words,
we claim that equations (4.87) and (4.88) belong to the same homotopy class, and,
in the CP, the solutions are then expected to be equally oscillatory to encourage their
maximal regularity at interfaces.
Thus, by such a continuity in n, similar oscillatory properties are expected to be
preserved in the quasilinear model (4.87), at least for sufficiently small n > 0. This
helps to detect the maximal regularity of solutions and define proper solutions of
the CP as those with the increasing regularity as n → 0, i.e., approaching C
∞
(and
analytic) regularity of the rescaled kernel in (4.90) for the linear PDE (4.88).
Oscillatory solutions for n > 0. The TW profiles for (4.87) solve the ODE
−λf =
| f |
n
f
(4)
for y > 0, f (0) = 0. (4.91)
In Section 3.7, equations, such as (4.91), occurred in various aspects of thin film
theory.In order todetectthecharacterof sign changesofsuch solutions,we introduce
the oscillatory components ϕ for (4.91) by setting
f (y) = y
γ
ϕ(s), s = ln y, where γ =
4
n
. (4.92)
Then F =|ϕ|
n
ϕ satisfies the ODE with the operator P
4
[F] given by (3.156),
F
(4)
+ 2(2µ − 3)F
+ (6µ
2
− 18µ + 11)F
+ 2(2µ
3
− 9µ
2
+11µ − 3)F
+ µ(µ − 1)(µ − 2)(µ − 3)F + λ
F
−
n
n+1
F = 0,
(4.93)
where µ =
4(n+1)
n
> 4. According to (4.92), the oscillatory character of TW so-
lutions near interfaces depends on the availability of periodic solutions of the ODE
(4.93). Existence, nonexistence, multiplicity, and stability of periodic solutions of
such higher-order equations are difficult
OPEN questions of general ODE theory.
© 2007 by Taylor & Francis Group, LLC
4 Korteweg-de Vries and Harry Dym Models 187
0 5 10 15
2.5
2
1.5
1
0.5
0
0.5
1
1.5
2
2.5
x 10
5
s
F(s)
(a) n = 2
0 5 10 15
6
4
2
0
2
4
6
x 10
4
s
F(s)
(b) n = 4
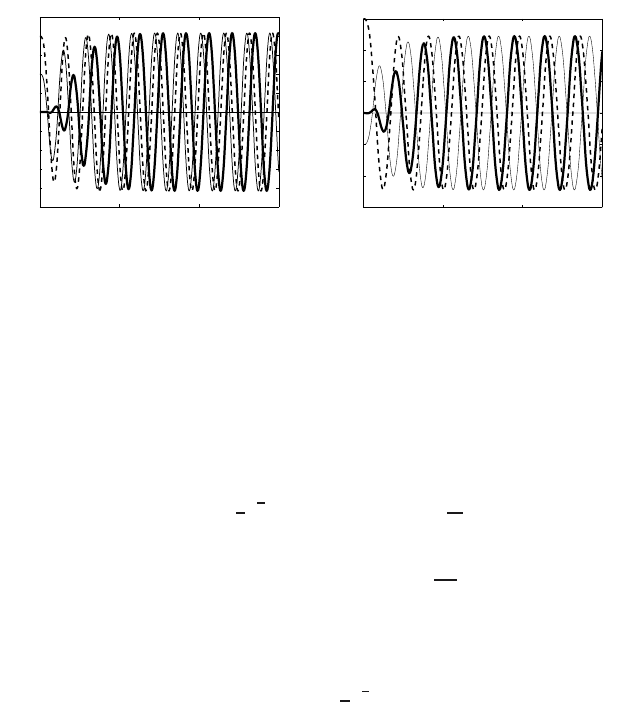
Figure 4.11 Convergence to stable periodic solutions of (4.93) with λ = 1forn = 2 (a) and
n = 4(b).
Stable periodic solutions for positive TW speeds. For λ>0, solutions of the
ODE (4.93) are oscillatory; see Figure 4.11. A single stable periodic motion was
always detected that agrees with a similar result for n = 0. As usual, the oscillation
amplitude becomes extremely small as n approaches zero, so we need extra scaling.
Limit n → 0. This scaling is
F(s) =
n
4
4
n
(η), where η =
4s
n
, (4.94)
where solves a simpler limit ODE (λ = 1),
(4)
+ 4
+ 6
+ 4
+ +
−
n
n+1
= 0. (4.95)
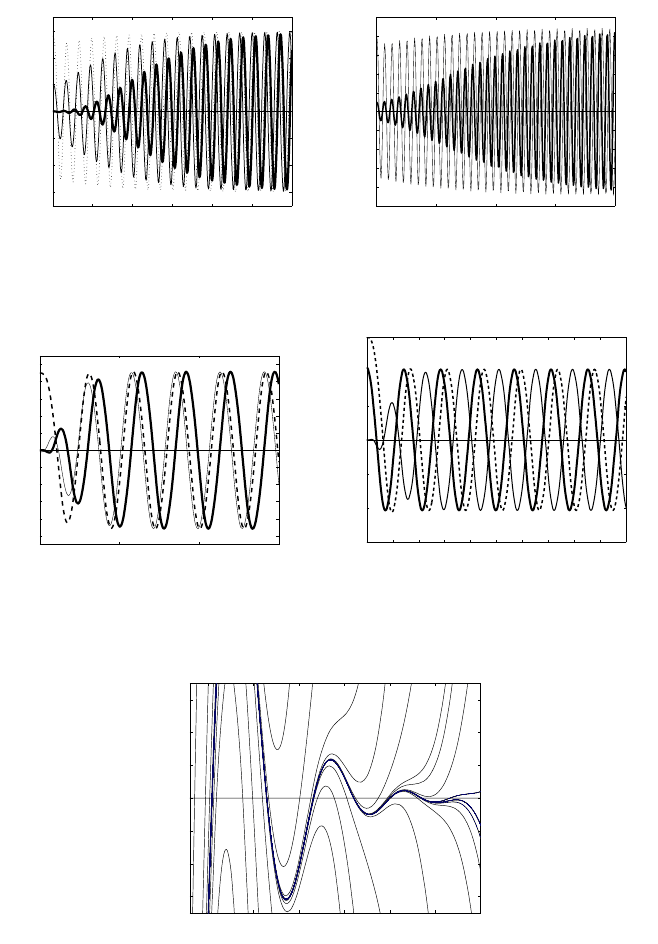
The stable oscillatory patterns for this equation are shown in Figure 4.12. For n =
0.2 in Figure 4.12(a), by scaling (4.94), the oscillatory component is estimated as
follows:
max|ϕ(s)|∼3 · 10
−4
n
4
4
n
∼ 3 ·10
−30
,
while
max|ϕ(s)|∼10
−93
for n = 0.08 in (b).
Limit n →∞. Then µ → 4, so the original ODE (4.93) approaches the following
equation with discontinuous nonlinearity:
F
(4)
∞
+ 10F
∞
+ 35F
∞
+ 50F
∞
+ 24F
∞
+ sign F
∞
= 0, (4.96)
whichalso admits a stable periodic solution,as shown in Figure 4.13. The same ODE
(4.96) occurred for a KS-type equation in Example 3.36, see Figure 3.16.
Unstable non-periodic behavior for negative speeds. For λ<0, two constant
equilibria are asymptotically stable, and numerically we find an unstable oscillatory
behavior in between; see Figure 4.14 for n = 1.3. This is a decaying behavior, which
reminds us the asymptotics in the linear case n = 0, but cannot be extended to the
interface at s =−∞.
This regularityand oscillatory ODE analysis again confirmsthatcompactons(4.77)
© 2007 by Taylor & Francis Group, LLC
188 Exact Solutions and Invariant Subspaces
0 20 40 60 80 100 120
3
2
1
0
1
2
3
x 10
4
η
Φ(η)
(a) n = 0.2
0 50 100 150 200
1
0.8
0.6
0.4
0.2
0
0.2
0.4
0.6
0.8
1
x 10
8
η
Φ(η)
(b) n = 0.08
Figure 4.12 Stable periodic oscillations in the ODE (4.95) for n = 0.2 (a) and n = 0.08 (b).
0 5 10 15
0.01
0.008
0.006
0.004
0.002
0
0.002
0.004
0.006
0.008
0.01
s
F(s)
(a) (4.93): n = 100
0 2 4 6 8 10 12 14 16 18 20
0.015
0.01
0.005
0
0.005
0.01
0.015
s
F
∞
(s)
(b) (4.96): n =+∞
Figure 4.13 Stable periodic patterns of the ODE (4.93) (λ = 1) change slightly for n = 100
(a) and n =+∞(b), equation (4.96).
7 7.5 8 8.5 9 9.5 10
3
2
1
0
1
2
3
x 10
6
s
F(s)
Figure 4.14 Unstable decaying structures of the ODE(4.93) withλ =−1forn = 1.3. Cauchy
data are F(0) = 2, F
(0) = F
(0) = 0, F
(0) =−2.67700981224690017... .
© 2007 by Taylor & Francis Group, LLC

4 Korteweg-de Vries and Harry Dym Models 189
are not maximal regularity solutions of the Cauchy problem for (4.76) and solve the
FBP specified above. This conclusion is true for similar (2m+1)th-order PDEs with
m ≥ 2.
4.3.2 Fast moving 2π-periodic solutions
Example 4.11 Consider a PDE similar to (4.13) with a linear perturbation on the
right-hand side, where parameters satisfy 16α − 4β + γ = 0,
u
t
= α(u
2
)
xxxxx
+ β(u
2
)
xxx
+ γ(u
2
)
x
+ δu + ε in IR × IR . (4.97)
Consider solutions (4.18) on W
3
. Then the DS (4.19) slightly changes,
C
1
= δC
1
+ ε,
C
2
= δC
2
+ µC
1
C
3
,
C
3
= δC
3
− µC
1
C
2
,
(4.98)
where µ = 6(β − 5α). This gives the following explicit 2π-periodic solutions:
(i) If δ = 0, the solutions exhibit a quadratic propagation with time,
u(x , t) = εt + A + B cos
x + µ
ε
2
t
2
+ At + D
(A, B, D ∈ IR ); (4.99)
(ii) If δ>0, the propagation is exponentially fast,
u(x , t) = e
δt
−
ε
δ
e
−δt
+ A + B cos
x + µ
A
δ
e
δt
−
ε
δ
t + D
. (4.100)
4.3.3 5D trigonometric subspaces
We begin with the fifth-order PDE (4.13) with α = 1,
u
t
= F[u] ≡ (u
2
)
xxxxx
+ β(u
2
)
xxx
+ γ(u
2
)
x
. (4.101)
Proposition 4.12
The only operator
F
in
(4.101)
preserving the 5D subspace
W
5
= L{1, cos x , sin x, cos2x , sin2x} (4.102)
is as follows:
F[u] = (u
2
)
xxxxx
+ 25(u
2
)
xxx
+ 144(u
2
)
x
. (4.103)
The algebraic manipulations yield the following invariance condition of W
5
:
9β − γ = 81,
16β − γ = 256,
from which β = 25, γ = 144, and (4.103)follows.
Example 4.13 (Quintic PDE on W
5
) The quintic nonlinear dispersion equation
(4.101), (4.103) possesses the solutions
u(x , t) = C
1
(t) + C
2
(t) cos x + C
3
(t) sin x + C
4
(t) cos2x +C
5
(t) sin 2x,
© 2007 by Taylor & Francis Group, LLC

190 Exact Solutions and Invariant Subspaces
C
1
= 0,
C
2
= 120(C
2
C
5
− C
3
C
4
+ 2C
1
C
3
),
C
3
=−120(C
2
C
4
+ C
3
C
5
+ 2C
1
C
2
),
C
4
= 120(2C
1
C
5
+ C
2
C
3
),
C
5
= 60(C
2
3
− C
2
2
− 4C
1
C
4
).
(4.104)
The nonnegative compacton [147, p. 4734] exists for λ<0,
u
c
(x , t) =−
λ
105
cos
4
1
2
(x − λt)
. (4.105)
This corresponds to the following explicit solution of the DS (4.104):
C
1
(t) =−
λ
280
, C
2
(t) =−
λ
210
cosλt, C
3
(t) =−
λ
210
sinλt,
C
4
(t) =−
λ
840
cos2λt, C
5
(t) =−
λ
840
sin2λt.
The DS (4.104) describes a finite-dimensional evolution near the compacton, and
possibly may detect its stability on the subspace W
5
. The ODE analysis here is harder
than that on W
3
in Example 3.17. According to (4.86), the compacton (4.105) satis-
fies the condition of the maximal regularity, so it is a solution of the CP.
It is easy to extend the above invariant analysis to the 7th-order PDE
u
t
= F[u] ≡ D
7
x
(u
2
) + β D
5
x
(u
2
) + γ(u
2
)
xxx
+ δ(u
2
)
x
, (4.106)
though such PDEs are still of no use in applications related to nonlinear dispersion
phenomena, [495]. It follows from Proposition 4.12, that F admits W
5
,if
β = 25, γ = 144, and δ = 0.
This operator is unique up to a multiple of (4.103).
4.3.4 7D trigonometric subspace
Take
W
7
= L{1, cos x , sin x, cos2x, sin2x , cos3x , sin 3x }. (4.107)
Proposition 4.14
The only operator
F
in
(4.106)
preserving
(4.107)
is
F[u] = D
7
x
(u
2
) + 77D
5
x
(u
2
) + 1876(u
2
)
xxx
+ 14400(u
2
)
x
. (4.108)
The invariance condition of W
7
is the linear system
256β − 16γ + δ = 4096,
1296β −36γ + δ = 46656,
625β − 25γ + δ = 15625,
which yields operator (4.108).
Example 4.15 (7th-order PDE on W
7
) The PDE (4.106), (4.108) on (4.107) is
u(x , t) = C
1
+C
2
cos x +C
3
sin x +C
4
cos2x +C
5
sin2x +C
6
cos3x +C
7
sin3x,
© 2007 by Taylor & Francis Group, LLC

4 Korteweg-de Vries and Harry Dym Models 191
C
1
= 0,
C
2
= 12600(C
4
C
7
− C
5
C
6
− C
3
C
4
+ C
2
C
5
+ 2C
1
C
3
),
C
3
=−12600(C
4
C
6
+ C
5
C
7
+ C
2
C
4
+ C
3
C
5
+ 2C
1
C
2
),
C
4
= 16128(C
2
C
7
− C
3
C
6
+ 2C
1
C
5
+ C
2
C
3
),
C
5
=−8064(2C
2
C
6
+ 2C
3
C
7
+ 4C
1
C
4
+ C
2
2
− C
2
3
),
C
6
= 9072(2C
1
C
7
+ C
3
C
4
+ C
2
C
5
),
C
7
=−9072(2C
1
C
6
+ C
2
C
4
− C
3
C
5
).
Concerning compactons, the following result holds:
Proposition 4.16
The only compacton admitted by
(4.106)
on
W
7
occurs for
u
t
= D
7
x
(u
2
) + 56D
5
x
(u
2
) + 784(u
2
)
xxx
+ 2304(u
2
)
x
, (4.109)
and it is stationary
(λ = 0)
,
u(x , t) = A sin
3
x,
where
A = constant > 0. (4.110)
Namely, substituting u(x, t) = A sin
3
(x − λt) into (4.106) yields λ = 0and
the coefficients indicated in the PDE (4.109). Then W
7
is not invariant. Despite its
sufficient regularity at the interfaces (O(x
3
) as x → 0
+
), (4.110) is governed by a
special FBP with the zero contact angle conditions and interface equations, and is
not a solution of the Cauchy problem. According to our conclusions in Example 4.9,
the Cauchy problem needs another maximal regularity, which is given by the TWs
f (x − λt), so that, on integration, keeping the leading term,
−λf = ( f
2
)
(6)
.
Then, instead of (4.83), the asymptotics behavior as y → 0is
f (y) = y
6
ϕ(s), where s = ln y, (4.111)
where the componentϕ satisfies a sixth-order ODE. As usual, for λ<0, there exists
the simple explicit solution
f (y) =−λ
6!
12!
y
6
> 0fory > 0.
Hence, the maximal regularity is f (y) = O(y
6
) as y → 0, which is much smoother
than O(y
3
) (here, y = x) given by (4.110).
On oscillatory patterns in the CP. The oscillatory behavior near interfaces occurs
for the signed seventh-order PDE
u
t
= D
7
x
|u|
n
u
in IR × IR (n > 0). (4.112)
This has the natural connection as n → 0
+
with the linear dispersion equation
u
t
= u
xxxxxxx
,
whose fundamental solution is oscillatory at both interfaces x =±∞.
For (4.112), the TW profiles f (y) solve the ODE
| f |
n
f
(6)
=−λ f for y > 0, f (0) = 0.
© 2007 by Taylor & Francis Group, LLC

192 Exact Solutions and Invariant Subspaces
0 5 10 15 20
1
0.8
0.6
0.4
0.2
0
0.2
0.4
0.6
0.8
1
x 10
5
s
F(s)
(a) n = 5
0 5 10 15 20
6
4
2
0
2
4
6
x 10
4
s
F(s)
(b) n = 500
Figure 4.15 Stable periodic behavior for (4.114), λ = 1, n = 5(a),andn = 500 (b).
Instead of (4.111), the oscillatory componentϕ is introduced as follows:
f (y) = y
µ
ϕ(s), s = ln y, with µ =
6
n
. (4.113)
Setting |ϕ|
n
ϕ = F yields a sixth-order ODE (similar odd-order equations occurred
in thin film analysis in Section 3.7)
P
6
[F] +λ
F
−
n
n+1
F = 0, with exponent γ =
6(n+1)
n
, (4.114)
where the linear operator P
6
is defined by the recursion (3.156). The stable periodic
behavior for (4.114), λ = 1, which creates changing sign TW patterns by (4.113), is
shown in Figure 4.15, where the part (b) corresponds to n = 500 and changes a little
forlargervaluesofn.Thenγ → 6, so the ODE admits the limit n →+∞,where
the discontinuous nonlinearity sign F occurs.
In order to see periodic oscillations for smaller n (actually, there is a numerical
difficulty already for n ≤ 4), we perform the scaling
F(s) =
n
6
6
n
(η), where η =
6s
n
, (4.115)
to get in the limit the following simplified ODE with the binomial linear operator:
(6)
+ 6
(5)
+ 15
(4)
+ 20
+ 15
+ 6
+
≡ e
−η
(e
η
)
(6)
=−λ
−
n
n+1
.
(4.116)
Figure 4.16 shows the stable periodic behavior for (4.116) with λ = 1. According to
scaling (4.115), the oscillatory component ϕ(s) gets extremely small,
max|ϕ|∼5 × 10
−10
for n = 0.5, and max|ϕ|∼2 ×10
−111
for n = 0.1.
For λ<0, periodic solutions of (4.114) are unstable; see Figure 4.17 for n = 15
that is obtained by shooting from s = 0 with prescribed Cauchy data.
4.3.5 Cubic and higher-degree operators
Example 4.17 (Cubic operators) Consider the following cubic operator:
F[u] = D
5
x
(u
3
) + β(u
3
)
xxx
+ γ(u
3
)
x
. (4.117)
© 2007 by Taylor & Francis Group, LLC
