Gardner M. Sixth Book of Mathematical Diversions from Scientific American
Подождите немного. Документ загружается.


113.
An infinite set of nested squares
they approach zero as
a
limit. Nevertheless,
the sum increases without bound! To prove
this we have only to consider the
terms in
groups of two, four, eight, and so on, begin-
ning with 113. The first group,
113
+
114,
su111s to inore than 112 because 1/:3 is greater
than
114,
and
a
pair
of fourths sums
to
112.
Similarly, the second group, 1It5
+
116
+
117
+
118, is more than 112 because each term
except the last exceeds 118, and a quadruple
of eighths sums to
112.
In
the same way the
third group, of eight
terins, exceeds 112be-
cause every term except the last (1116)
is
greater than 1116, and 8/16; is 112. Each suc-
ceeding
group
can
thus be shown to exceed
112, and since the number of such groups is

114.
What
is
the limit of area for the colored portion?
urllimitecl the series must diverge. It does
so, however,
with infuriating slowness. Tlie
first
100
terms, for instance, total only
a
bit
rnore
than
5.
To
reach
100
requires more
than
2""errns, but less than 2144 terms.
(I
am indebted to Daniel Asimov for s1.ipp1~-
ing these up~er and lower bounds.)
In
1968
John
\V.
TVre~lch, Jr., calculated the exact
number of terms at
\vhich the series has
a
partial sum exceeding
100.
The
number
of
terms is
15,092,688,622,113,788,:323,693,-
563,264,538,101,449 ,8859,497.
The harmonic series is involved in ari
amusing problem that al)peared in the
Pi
1111
El~.silon
Journc~l
for April,
1954,
and
more recently in
Pzrzzle-Jlatlz,
a
book
by
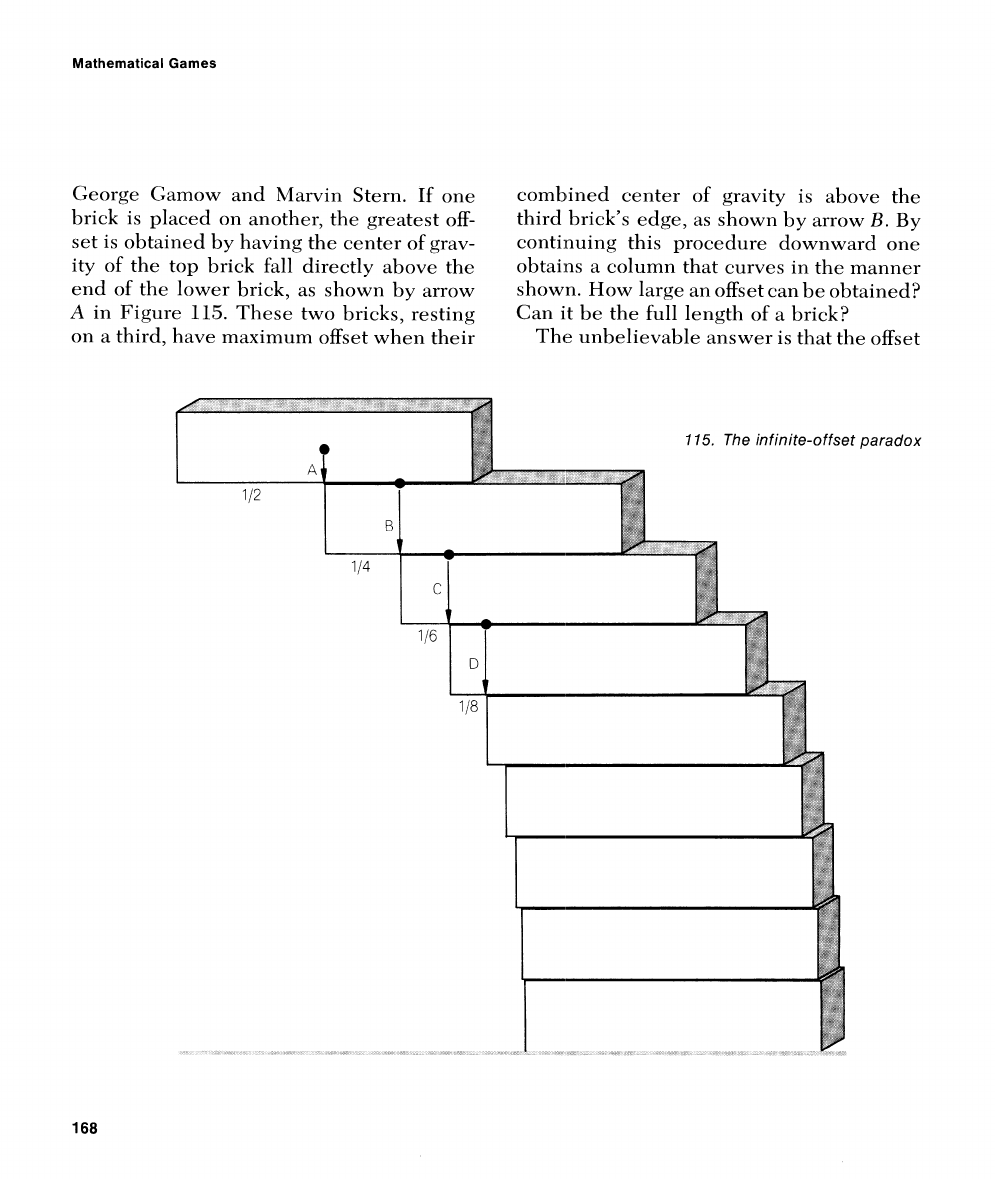
Mathematical Games
George Camow and hlarvin Stern.
If
one
comblined center of gravity is above the
brick is placed on another, the greatest off-
third brick's edge, as shown
by arrow
B.
By
set is obtained
by having the center of grav-
continuing this procedure downward one
ity
of the top brick fall directly above the
obtains a column that curves
in the manner
end of the lower brick, as shown by arrow
shown. How large an offset can be obtained?
A
in Figure
115.
These two bricks, resting
Can it be the full length of a brick?
on
a
third, have maxinium offset when their
The unbelievable answer is that the offset
115.
The infinite-offset
'
paradox

Limits of
Infinite
Series
can be as large as one wishes! The top brick
projects half a brick's length.
The second
projects
114,
the third
116:
and so on do\vn.
LYit11 an unli~nited supply of bricks the off-
set is
.the limit of
This is simply the harmonic series with
each term cut in half.
Since the sum of the
harnlonic series can be made larger than
any number we care to name, so
can half
its sum. In short, the series diverges, and
therefore
the offset can be increased with-
out limit. As
Lve have seen, slicll
a
series
diverges so slowly
that it would take a great
nlany bricks to achieve even
a
small offset.
FYit11
52
playing cards, the first placed so
that its end is flush
with
a
table edge, the
maximum overhang is a little
illore than
2l14
card lengths
[.s.ec
Figure
11
6.1.
Readers rnay
enjoy seeing if they can build an offset,
using one deck, that exceeds two card
lengths.
The harmonic series has
inany curious
properties.
If
every term containing the
digit
9
is crossed out, the remaining terms
116.
The overhang of
a
deck
of
cards

Mathematical Games
form
a
convergent series. If tlie denomina-
tor of each term is raised to the
same power
11,
and
11
is greater than 1, the series con-
verges. If every other sign, starting with the
first, is changed to minus, the resulting
series
chokes off on
tlie natural logarithm of 2, a
number slightly
smaller than
.7.
Does the
value of the series ever reach (after 1, of
course) a number that is
an
integer? If there
were
a
sin~ple formula for expressing the
value of the series for
11
terins, this might be
easily answered, but there is no
such for-
mllla. -411 ingenious odd-even argllment,
however, that goes back at least to 1915 (the
details are given on page
48 of the
ilrnerica~~
Jlutl~en~c~tical 31011tl~/!j
for January, 1934)
shows that the series never reaches an
integral sum.
If all the terms of an infinite series are
positive, it clearly does not matter how the
terms are grouped or rearranged; the lirnit
renlains the same. But if there are neg,
CI
t' ive
terms, it sometimes makes a big difference.
From the
seventeenth century to the middle
of tlie nineteenth, before laws of limits were
carefully
forn~ulated, all sorts of disturbing
paradoxes were produced by juggling the
plus and
niinus terms of various infinite
series. Luigi Cuido Grandi,
a
mathema-
tician at the University of
ha, considered
the simple oscillating series
l
-
1
+
1
-
l
+
1
-
.
. . .
If one groups the terms
(1
-
1)
+
(1
-
1)
+
(1
-
1)
+
. .
.
,
the limit is
0.
If
onegroupstheml-(1-1)-(1-1)-
. .
.
,
changing the signs within parentheses as
required, the
sum is
1.
This slio\vs, Gnindi
said, how God could take
a
universe with
parts that added up to nothing and then, by
suital~le rearranging, create something.
The correct
lirnit for the original series,
Grantli declared, is 112. He supported this
11y a parable. ,4 father wills a precious stone
to two sons with the proviso that every year
the stone go from one to the other. If the
value of the stone is
1, then its value to each
son is the sum of
1
-
1
+
1
-
1
+
.
.
.
.
Since
the two brothers share the legacy equally,
this value must be 112. llany distinguished
mathematicians joined in the controversy
over this series. Both
Ciottfried \T1ilhelm von
Leibniz and Leonhard Euler agreed on the
112, although for someu,hat different rea-
sons. Today the series is recognized as
divergent, so that no meaningful limit can
be assigned to it.
An even worse instance is provided
by
the series
1
-
2
+
4
-
8
+
16
-
. . . .
Group
it
1
+-
(-2
+
4)
+
(-8
+
16)
+
. . .
ancl you
obtain the series
1
+
2
+
8
+
16
+
. . .
,
which diverges to positive infinity. Group it
(1
-
51)
+
(4
-
8)+
(16-32)+
. .
.
and
you
get the series
-
1-4- 16-64-.
. .
,
which
diverges to infinity in
the negative clirec-
tion! The climax to all this infernal hubbub
came
in 1854 when Georg Friedrich Rern-
hard Riemann, the German nlathematician
now well known for his non-Euclidean
geonletry, proved
a
truly reinarkable
theorem. Whenever the liillit of an infinite
series can be changed
by regrouping or
rearranging the order of its
terins, it is called
co~~ditiot~ully
convergent in contrast to an
clhsolutely
convergent series, which is un-

Limits
of
Infinite Series
affected by such scrambling. Conditionally
coilvergei~t series always have negative
terms, and they always diverge when all
their
terins have been rliade positive. Kie-
Inarlil showed that any coilditiolially con-
vergent series (such as the one previously
cited that chokes off
on the natural logarithm
of 2) can be suitably rearranged to give a
limit
that is any desired number whatever,
rational or irrational, or even made to
diverge to infinity in either direction.
Eve11 an infinite series without negative
terms, if it diverges,
car1 cause serious trou-
ble if one tries to handle it with rules that
apply only to finite and converging series.
For
exanlple, let
.s
be the infinite, positive
sulrl of 1
+
2
+
4
+
8
+
16
+
. . .
.
Then
2x
nlust equal 2
+
4
+
8
+
16
+
.
. .
.
This new
series is nierely the old series ~nilius
1.
Therefore
2x
=
x
-
1,
wllicli reduces to x
=
-1.
Thus we seem to have proved that
-1
is irlfiriite and positive. One can sympathize
with the Norwegian inathematician Niels
Henrik Abel,
who wrote in 1828: "The
di\-ergent series are the invention of the
devil, and it is
a
shame to base on thein any
demon st ratio^^
whatever."
Addendum
S.
W.
Gololnb was the first of several mathe-
maticia~ls to point out that
I
was not quite
accurate in
saying that a divergent series
could
not be given
a
nleaningful.sum. "After
colivincirig our undergraduates that diver-
gent series are tlie invention of the devil,"
Golomb wrote, "we let them learn in
graduate school that
these series can be
'surn~ned' after all, if one is sufficiently care-
ful to
define new kinds of summnation rules
(e.g., Ceshro summation, Abel summation,
etc.)."
Golomb went
011
to say that G. H.
Hardy's
Dicergerlt
Series (New York: Ox-
ford Press, 1949) is
a
remarkable book in
which
such sulnn~atiori techniques are ex-
plained. The series
1
-
1
+
1
-
1
+
1
. . .
,
for example, has both
a
CesAro sum and an
A4bel sum of 112,
as
Leibiliz and Euler main-
tained.
Tlle reader is referred to Hardy's
posthumous
book for
a
fascinating survey of
the field.
Answers
If Achilles runs seven tirrles as fast as the
tortoise,
which has
a
head start of 100 yards,
the total distance .Achilles travels, before
overtaking
the tortoise, is the limit of the
series
Each
terin is se\.eri tilrles the next term.
Usiqg the trick explained: \ve lets equal the
series: then multiply each side
1)y 7:
This series, after
700,
is the original series.
Therefore
7s
=
700
+
s,
or 6x
=
700,
and x
=
116Y3,
the number of yards Ilchilles travels.
The
hounciiig ball comes to rest after
traveling a
distalice equal to the first foot

Mathematical Games
that it falls, plus the sum of 213
+
219
+
2/27
+
.
.
. .
The same procedure is applied
(multiplying by the constant factor of 3) to
obtain a limit of one foot for the series. Thus
the total
distance traveled by the ball, be-
fore it comes to rest after an infinite number
of bounces, is
1
+
1,
or two feet.
The Hungarian problem of the colored
squares calls for the limit of the following
series:
This is also
a
geometric progression, with
each term 918 of the next one. As before, we
can use the algebraic trick, or-what
amounts to the same thing-use the follow-
ing formula for the sum of
a
converging
series in geometric progression:
where
r
is the ratio of adjacent terms (in this
case
918) and
x
is the largest term of the
series (in this case
119). The limit is 1.
Therefore as the
number of coloring opera-
tions increases without bound, the colored
area of the unit square approaches the area
of
1.
In other words, the limit is
a
fully
covered square. Of course this could be
achieved in practice only if a coloring pro-
cedure could be devised in which the time
required for each step would decrease in
a
converging series.
The colored-squares problem was taken
from
Hungarian
Problem
Book
I,
translated
by Elvira Rapaport, in the Random House
New Mathematical Library (New York:
Random House, 1963).
References
An Introduction to the Theory of Infinite Series.
T.
J.
I'a. Bromwich. London: Macmillan and
Co., Limited,
1942.
Summation of Infinitely Sm(ll1 Quantities.
I.
P.
Natanson. Boston:
D.
C. Heath and Co., 1963.
Limits.
Norman hliller. Waltham, hlass.: Blais-
dell Publishing Co., 1964.
Limits and Continuity.
William
K.
Smith. New
York:
hlacmillan, 1964.
A
Coilcept of Limits.
Donald
W.
Hight
New
York: Prentice-Hall, 1966.
Injinzte Series.
Earl
D.
Rainville. New York:
hlacmillan, 1967.
Modern Science and Zeno's Paradoxes.
Adolf
Grunbaum. hliddletown, Conn.: Wesleyan
University Press, 1967.
"Partial
Sums
of the Harmonic Series."
R.
P.
Boas,
Jr.,
and
J.
J.
Wrench,
Jr.
The American
Jfathematical Monthly,
Vol. 78, No. 8 (October
197l),
pp.
864-870.

18.
Polyiamonds
IN 1965
CHARLES
SCRTBNER'S
SONS
pub-
lished
Polyominoes,
a book of great interest
to mathematics puzzlers. The author is Solo-
mon
W.
Golomb, a mathematician then as-
sociated with the California Institute of
Technology's Jet Propulsion Laboratory and
professor of engineering and mathematics
at the University of Southern California. It
was in 1953 that Golomb, a student at Har-
vard University, coined the term "polyom-
ino" for any flat figure formed by joining
unit squares along their edges. Since a
"domino" consists of two attached squares,
Golomb proposed calling a three-square
"
figure a tromino," a four-square figure a
"
tetromino" and so on.
Among puzzle fans the 12 pentominoes
-
all the different ways of uniting five unit
squares-proved the most popular. So in-
triguing were the combinatorial problems
posed by these 12 little shapes that working
with them became something of a national
pastime. Sets of plastic pentominoes were
marketed both in this country and in Brit-
ain, and Golomb found himself swamped
with suggestions for new problems and re-
quests for more information. Then, to the
delight of all pentomino buffs, he assembled
in one profusely illustrated volume every-
thing of interest he had learned about the
pentominoes and their square-cornered
cousins.
In this chapter we consider a triangular
cousin. It is mentioned briefly in Golomb's
book and there are scattered references to
it in a few journals, but most of what is
known about this new recreation has been
discovered since 1965. It is a field with
many fundamental problems yet to be
solved and a rich supply of patterns and
theorems still to be discovered.
Golomb had pointed out as early as 1954,
in "Checkerboards and Polyominoes," in
The American Mathematical Monthly,
December, 1954, that a recreation similar to
polyominoes could be based on pieces
formed by joining unit equilateral triangles.
The Glasgow mathematician
T.
H.
O'Beirne,
writing in the
New Scientist
in 1961, pro-
posed calling such shapes "polyiamonds."

Mathematical Games
Taking his etymological cue from Colomb,
O'Beirne reasoned that if
n
"diamond" con-
sists of two attached triangles,
a
figure
forlned by three triangles should be called
a
"triamond," four triangles
a
"tetriamond"
and so on up through "pentiamond,"
"hexiamond," "heptiarnond" and higher
11-iamo~lds. Ob\~~iously there is only one
form of diamo~~cl and trianlond, and the
reader
can quickly convince hilnself that
there are three
tetriamonds and four pent-
iamonds. (As with polyominoes, mirror
reflectiorls of asynlrrletrical forms are not
usu:tlly considered different.) The hex-
iamonds, by a pleasing coincidence with
the
penton~inoes, are exactly 12in number.
There are 24
heptiamonds, 66 octiamonds,
and 160 order-0 figures (one with
a
hole).
Beyond this no accurate
counts have been
established.
The
12 hexiamonds are shown in Figure
117.
with appropriate names, most of them
first proposed by O'Beirne. The reader is
invited to copy these 12 shapes on
a
sheet
of cardboard
and carefully cut them out.
The coloring on the shapes should be ig-
nored. It is best to use cardboard that is
the same
on
both sides, so that asymmet-
rical pieces can
be turned cn7er at will. It is
good to have
a
supply of isometric paper
on
hand for ease in recordirlg patterns.
It is
obvious that any pattern formed by
two or more hexiamonds must contain a
nunnber of unit triangles that is evenly di-
visible by
6.
\F7e car1 go further. By coloring
the pieces as shown we see that every piece
except the last two (sphinx
and yacht) are
"balanced" in the sense that they contain
11
7.
The
12
hexiamonds
three triangles of each color. Therefore any
figure made
by fitting together two or more
balan~:ed hexian-~onds rnlist itself be bal-
anced. The yacht and
s~hinx are each un-
balanc-ed four to two. If one of these pieces
appears in a figure, the figure
must be un-
balanced
by an excess of two triangles. If
110th pieces are used, the figure must be
either. balanced (the yacht
and sphinx being
so placed that they compensate for each
other) or
urlbala~lced with an excess of four
triangles. This provides a powerful check
for eliminating
many figures that otherwise
might be thought possible.
Collsider, for example, the equilateral
triangle of order-6
[Figure
118,
top].
It con-
tains 36 unit triangles; it is the
oilly tri-
angle
within the range of the 12 hexiamonds
that
has a number of unit triangles evenly
divisible by
6.
One could waste many hours
vainly trying to construct this triangle with
six
ht:xiamonds. If it is colored as shown,
however, we
find that it contains an excess
of six triangles of one color. Since the maxi-
mum achievable excess is four, the figure is
seen ;it once to be impossible.
Attention
turns naturally to the parallelo-
grams. Only the 3
x
3 and 6
x
6
diamonds
(rhombi) contain the proper number of tri-
angles. The smaller
dianlond is easily found
to be impossible, but the
6
x
6 has scores of

