Гайдук А.Р. Непрерывные и дискретные динамические системы
Подождите немного. Документ загружается.


240
t
At
eCe
)(
1
0
ε+γ
≤
,
,0
∞
≤
≤
t
где
1
C
– достаточно большое число;
ε
– любое положительное число.
П.5.11. Определитель
ttrAAt
ee
)(
det =
. (П.41)
Здесь величина
∑ ∑
=
σ
=
λ==
n
i i
iiii
naAtr
1 1
называется следом матрицы
A
. Как и собственные числа
)(
A
i
λ
, эта ве-
личина является инвариантом относительно преобразования подобия
(П.17). Здесь
i
n
– кратность собственного числа
i
λ
, а
σ
– число различ-
ных собственных чисел матрицы A.
Из формулы (П.41) следует, что переходная матрица
At
e
при всех
t
неособенная и имеет обратную. Этой матрицей является
At
e
−
.
П.5.12. Производная переходной матрицы
At
e
по переменной
t
на-
ходится путем дифференцирования по
t
ряда (П.28), т.е.
.)
!
2
!
1
(
22
AeAe
tAAt
E
dt
d
dt
de
AtAt
At
==+++= K
Следовательно, матрица
)]([ tФe
ij
At
=
удовлетворяет матричному
дифференциальному уравнению
)()( tAФtФ =
&
при
.)0( EФ
=
П.5.13. Интеграл от матрицы
At
e
. Если матрица
A
имеет об-
ратную, то интеграл от
At
e
можно найти по формуле
.)(
0
0
0
0
111
∫ ∫
−==τ=τ
−τ−τ−τ
t
t
At
At
t
t
A
t
t
AA
eeAeAdAeAde
(П.42)

241
Если матрица A не имеет обратной, то интеграл от
At
e
находится
путем интегрирования каждого элемента матрицы
At
e
в отдельности.
П.6. Квадратичные формы
П.6.1. Пусть
][
i
xx =
– вектор из пространства
n
R
. Функция многих
переменных
n
xx ...,,
1
вида
∑
=+++=
=
n
ki
kiiknnnn
xxxxxxxxxV
1,
21121111
,...)(
γγγγ
(П.43)
где
,
kiik
γγ
=
называется ква драт ич но й фо рмой в
n
R
. В частности,
при
2
=
n
имеем из выражения (П.43)
.2)(
2
2222112
2
111
xxxxxV
γγγ
++=
(П.44)
С помощью симметрической матрицы коэффициентов
,
...
...
...
21
22221
11211
=Γ
nnnn
n
n
γγγ
γγγ
γγγ
где
kiik
γ=γ
,
форму (П.43) удобно записывать следующим образом:
).,()( xxxxxV
T
Γ=Γ=
(П.45)
Действительно, полагая в выражении (П.45)
2
=
n
и выполняя ум-
ножение, получим
=
γγ
γ+γ
=
γγ
γγ
=
222121
212111
21
2
1
2221
1211
][)(
xx
xx
xx
x
x
xxV
T
,
2222121221211111
xxxxxxxx
γγγγ
+++=
что совпадает с выражением (П. 44), так как
.
2112
γγ
=

242
П.6.2. Квадратичная форма является п ол ожи те ль но опр еде ле н-
ной в пространстве
n
R
, если при любом векторе
0
≠
x
из
n
R
.0)( >Γ= xxxV
T
Если же при любом
0
≠
x
из
n
R
,0)( ≥Γ= xxxV
T
то квадратичная форма
xx
T
Γ
называется по ло жи те льн о п олуо пре-
дел ен но й (н еотр ица те ль но й).
П.6.3. Так как матрица Г квадратичной формы
xx
T
Γ
является
симметрической, то эта квадратичная форма является положительно
определенной, если все собственные числа
)(Γλ
i
матрицы
Γ
строго
положительны [12].
Критерий Сильвестра. Квадратичная форма
xx
T
Γ
является по-
ложительно определенной, если выполняются
n
неравенств
;0
...
.............
...
1
111
>
γγ
γγ
=∆
iii
i
i
....,,1 ni
=
(П.46)
Примером неотрицательных квадратичных форм могут служить
квадратичные формы (П.45) с матрицей
T
SS=Γ
, (П.47)
где S – произвольная
kn
×
матрица, причем
nk
≤
.
П.6.4. Если симметрическая матрица Г удовлетворяет условиям
(П.46), то она, как и форма (П.45), называется п оло жи тель но оп ре-
дел ен но й, и обозначается Г > 0.
Например, если в (П.47)
nk
=
и ранг
,][ nS
=
ρ
то Г – положитель-
но определенная матрица, т.е. при
nk
=
и
nS
=
ρ
][
матрица
0>=Γ
T
SS
.
П.6.5. Если среди собственных чисел
)(Γλ
i
матрицы
Γ
имеется
хотя бы одно не отрицательное число
0)( ≥Γλ
ν
, а остальные положи-

243
тельны, то матрица
Γ
является положительно полуопределенной (не -
отриц ате ль но й) и обозначается
0
≥
Γ
.
Неотрицательными матрицами, в частности являются матрицы типа
(П.47).
П.6.6. Квадратичная форма
xx
T
Γ
удовлетворяет неравенствам
,
22
1
xxxx
n
T
λ≤Γ≤λ
(П.48)
где
n
λλ ,
1
– наименьшее и наибольшее собственные числа матрицы Г;
x
– норма (третья) вектора
x
(см. П.1.33).
244
П.7. Преобразование Лапласа
Непрерывное и дискретное (z-) преобразования Лапласа определя-
ются соотношениями:
∫
∞
−
=
0
)()( dtetgpg
pt
,
k
k
zkTgzg
−
∞
=
∑
=
0
)()(
.
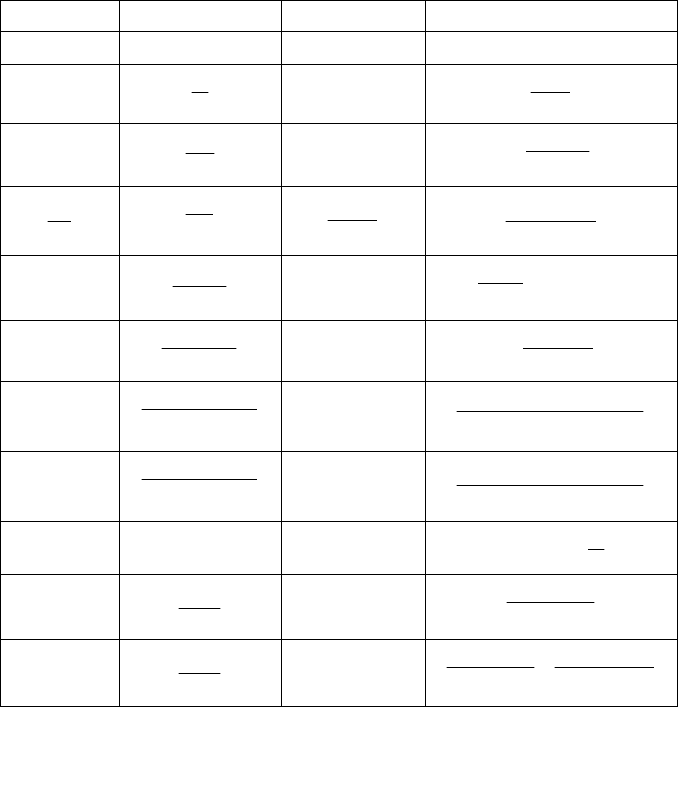
Изображения по Лапласу непрерывных и дискретных функций
)(tg
)(pg
][kTg
)(zg
)(t
δ
1
][kT
δ
1
0
=
z
)(1 t
p
1
][1 kT
1
−
z
z
t
2
1
p
kT
2
)1( −z
z
T
!
2
2
t
3
1
p
!
2
][
2
kT
3
2
)1(!2
)1(
−
+
z
zzT
t
e
α−
α+
p
1
kkT
de =
α−
d
z
z
−
,
T
ed
α−
=
t
te
α−
2
)(
1
α+p
T
kTe
α−
2
)( dz
zd
T
−
)sin( te
t
β
α−
22
)( β+α+
β
p
]sin[ kTe
kT
β
α−
22
)cos(2
)sin(
dTzdz
Tzd
+β−
β
)cos( te
t
β
α−
22
)(
β+α+
α
+
p
p
]cos[ kTe
kT
β
α−
22
2
)cos(2
)cos(
dTzdz
Tzdz
+β−
β−
)(
τ
−
δ
t
p
e
τ−
][
τ
−
δ
mkT
T
mz
m
τ
=
−
,
)(1
τ
−
t
p
e
pτ−
][1
τ
−
kT
)1(
1
1
−
−µ
zz
τ
−
t
2
p
e
pτ−
τ
−
kT
211
)1()1(
−
+
−
τ
−
µ
−µ−µ
zz
T
zz
T
Примечание. Справки по
µ
и
τ
на следующей странице.
245
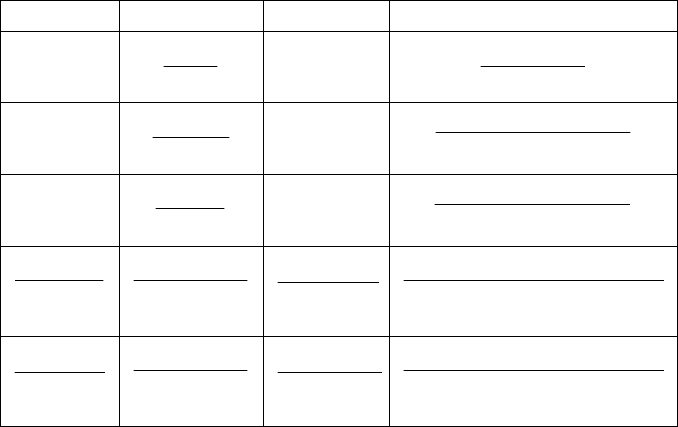
Продолжение
)(tg
)(pg
][kTg
)(zg
)( τ−α− t
e
α+
τ−
p
e
p
][
τ−α− kT
e
)(
1
)(
dzz
e
T
−
−µ
τ−µα−
)(sin τ−β t
22
β+
β
τ−
p
e
p
][sin τ−β kT
)1cos2(
sinsin
21
+β−
βθ+βϑ
−µ
Tzzz
z
)(cos τ−β t
22
β+
τ−
p
pe
p
][cos τ−β kT
)1cos2(
coscos
21
+β−
βθ−βϑ
−µ
Tzzz
z
)(
)(sin
τ−α
τ
−
β
t
e
t
22
)( β+α+
β
τ−
p
e
p
][
][sin
τ−α
τ−β
kT
e
kT
)cos2(
)sinsin(
221
dTzdzze
dzd
+β−
βθ+βϑ
−µατ−
µ
)(
)(cos
τ−α
τ−β
t
e
t
22
)(
)(
β+α+
α+
τ−
p
ep
p
][
][cos
τ−α
τ−β
kT
e
kT
)cos2(
)coscos(
221
dTzdzze
dzd
+β−
βθ−βϑ
−µατ−
µ
Примечание. Здесь
)(pg
– изображение функции
)(1)( ttg
,
)(zg
–
z-изображение функции
][1)(][)( kTtgkTgtg ==
∗
, где
∑
∞
=
−δ=
0
)(][1
l
lTkTkT
или
][1)(][)( kTtgkTgtg τ−=τ−=τ−
∗
.
Значение
µ
подбирается пользователем таким, чтобы при заданном
τ
выполнялось условие
TT
µ
≤
τ
<
−
µ
)1(
.
Величины:
τ
−
µ
=
ϑ
T
,
T)1(
−
µ
−
τ
=
θ
.

246
ЛИТЕРАТУРА
1. Андреев Ю.Н. Управление конечномерными объектами. М.: Нау-
ка, 1976.
2. Гайдук А.Р. Математические основы теории систем автоматического
управления. М.: Испо-Сервис, 2002.
3. Гайдук А.Р. К исследованию устойчивости линейных систем // Ав-
томатика и телемеханика 1997. № 3. Стр. 153 – 162.
4. Гантмахер Ф.Р. Теория матриц. М.: Наука, 1988.
5. Демидович Б.П. Лекции по математической теории устойчивости.
М.: Наука, 1967.
6. Деч Г. Руководство к практическому применению преобразования
Лапласа и z-преобразования. М.: Наука, 1971.
7. Иванов В.А. и др. Математические основы теории автоматического
регулирования. Учебное пособие для вузов. Под ред. Б.К. Чемодано-
ва. М.: Высшая школа, 1971.
8. Калман Р., Фалб П., Арбиб М. Очерки по математической теории
систем. М.: Наука, 1971.
9. Квакернаак Х., Сиван Р. Линейные оптимальные системы. М.: Мир,
1977.
10. Корн Г., Корн Т. Справочник по математике для научных работников
и инженеров. М.: Наука, 1968.
11. Лазарев Ю.Ф. MATLAB 5.х. Киев: Издательская группа BHV, 2000
(серия Библиотека студента).
12. Маркус М., Минк Х. Обзор по теории матриц и матричных нера-
венств. М.: Наука, 1972.
13. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. М.:
Наука, 1970.
14. Фихтенгольц Г.М. Курс дифференциального и интегрального исчис-
ления. Т. 1, 2, 3. М.: Наука, 1969.
15. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчис-
ление. М.: Наука, 1969.

247
Анатолий Романович Гайдук
Доктор технических наук, профессор
Непрерывные и дискретные
динамические системы
Редактор Б.Р. Гочияев
Компьютерная верстка Т.И. Соловей
Корректор Е.В. Домбровская
Сдано в набор16.02.2004 Подписано в печать 01.04.2004
Печать офсетная. Усл.печ.л. 16
Тираж 500 экз.
Отпечатано в ЗАО “Невинномысская городская типография”
357700, Ставропольский край, г. Невинномысск,
ул. Первомайская, 66-а.

248
