Гайдук А.Р. Непрерывные и дискретные динамические системы
Подождите немного. Документ загружается.

А.Р. ГАЙДУК
НЕПРЕРЫВНЫЕ И ДИСКРЕТНЫЕ
ДИНАМИЧЕСКИЕ СИСТЕМЫ
2-е издание, переработанное
и дополненное
Рекомендовано
Министерством общего и профессионального образования
Российской Федерации в качестве учебного пособия
для студентов, обучающихся по специальностям:
210100 – Управление и информатика в технических системах,
210200 – Автоматизация технических процессов и производств
МОСКВА
Учебно-методический и издательский центр
УЧЕБНАЯ ЛИТЕРАТУРА
2004

2
ББК 32.965
Г 14
Таганрогский государственный радиотехнический университет
Гайдук А.Р.
Г-14 Непрерывные и дискретные динамические системы. –2-е изд.
перераб.-М.: Учебно-методический и издательский центр «Учебная лите-
ратура». 2004.- 252с.
Рецензенты:
Кафедра «Информационные и управляющие системы» РГАСХМ
(зав. каф. – д.т.н., проф. Р.А. Нейдорф);
д.т.н., проф. Н.Н. Прокопенко, ЮРГУЭС
В книге излагаются математические методы описания и анализа не-
прерывных и дискретных динамических систем на основе системного под-
хода. Рассматривается взаимосвязь математических моделей вход-выход и
моделей в переменных состояния, вопросы реализации моделей вход-
выход, а также методы исследовании непрерывных и дискретных динами-
ческих систем при детерминированных и случайных воздействиях.
Книга предназначена для специалистов, занимающихся разработкой
современных динамических систем, а также для студентов, магистрантов
и аспирантов соответствующего профиля.
ISBN –5-8367-0025-X
ББК 32.965
Г 14
© Авторы, указанные на
титульном листе, 2004

3
ОГЛАВЛЕНИЕ
Предисловие………………………………………………………………
4
Г л а в а 1. Математические модели систем……………………...…. 7
§ 1.1. Основные понятия и определения ………………………………. 7
§ 1.2. Общие формы моделей динамических сис
тем…………………..
12
§ 1.3. Аналитический метод построения моделей…………………….. 22
Г л а в а 2. Решение уравнений динамических систем…………….
38
§ 2.1. Канонические формы моделей в переменных состояния………
38
§ 2.2. Общие свойства решений дифференциальных уравнений…….. 49
§ 2.3. Решение линейных дифференциальных уравнений…………….
67
§ 2.4. Решение систем дифференциальных уравнений……………….. 76
§ 2.5. Определение реакции динамических систем……………………
94
Г л а в а 3. Преобразование моделей ди
намических систем………
106
§ 3.1. Переход от уравнений в переменных состояния
к уравнениям вход-выход………………………………………………..
106
§ 3.2. Обратный переход от моделей вход-выход к моделям
в пере
менных состояния…………………………………………………
117
§ 3.3. Задача реализации моделей вход-выход……………………….... 130
§ 3.4. Преобразование структурных схем………………………………
133
§ 3.5. Преобразование структурных схем по уравнениям
в переменных состояния………………………………………………...
146
§ 3.6. Полиномиальный метод реализации моделей вход-выход……..
153
Г л а в а 4. Динамические системы при случайных воздействиях.
162
§ 4.1. Случайные воздействия и процессы……………………………..
162
§ 4.2. Случайные векторные процессы…………………………………
171
§ 4.3. Статистические характеристики выходных переменных
в ус
тановившемся режиме……………………………………………….
175
§ 4.4. Переходные процессы при случайных воздействиях…………... 183
§ 4.5. Вычисление диспер
сии выходной переменной………………….
189
Г л а в а 5. Дискретные динамические системы…………………… 193
§ 5.1. Дискретные переменные и их модели…………………………… 193
§ 5.2. Уравнения дискретных систем…………………………………...
198
§ 5.3. Решения разностных уравнений………
………………………….
204
§ 5.4. Решение систем разностных уравнений………………………… 207
Заключение………………………………………………………………
213
Приложения………………………………………………………………
215
Литература………………………………………………………………..
246

4
ПРЕДИСЛОВИЕ
Динамические системы - это объекты, наиболее часто встречающие-
ся в окружающем нас мире. Это и искусственные технические или фи-
нансовые системы и естественные системы, такие как солнечная система
или, скажем, горная система Кавказа. Методы изучения процессов, про-
текающих в этих системах, составляют предмет теории систем. Наиболее
широкое применение эти методы находят при исследовании автоматиче-
ских систем управления, которые практически всегда являются динами-
ческими с высокой скоростью протекания процессов.
Любая система управления создаётся с целью обеспечения желаемо-
го хода некоторого процесса. Система автоматического управления авто-
матически, без участия человека, поддерживает значения некоторых ве-
личин, определяющих ход управляемого процесса, на заданном уровне,
либо изменяет их в соответствии с целью управления.
Для выполнения этой задачи управляющая часть системы, называе-
мая регулятором, формирует управляющие воздействия – управления,
которые обеспечивают либо компенсацию отклонений, возникающих под
влиянием тех или иных возмущений, либо целесообразное изменение
управляемых величин системы. Управления, очевидно, должны быть
сформированы так, чтобы ход процесса изменялся в нужном направлении
и с определенной скоростью. Для этого необходима информация о цели
управления, а также информация о характере влияния управляющих воз-
действий и возмущений на ход процесса. Последнюю можно получить на
основе тех законов природы, в соответствии с которыми протекает
управляемый процесс.
С другой стороны, в науке и технике все известные законы природы
описываются некоторыми математическими уравнениями. Поэтому для
решения разнообразных проблем управления и анализа движений дина-
мических систем необходимы математические методы решения и иссле-
дования свойств решений алгебраических и дифференциальных уравне-
ний.
Познание причины одного
только явления даёт возможность
нашему уму постичь и установить
другие явления без необходимости
прибегать к помощи опыта…
Галилео Галилей

5
Основной и наиболее сложной здесь является проблема исследова-
ния зависимости характера и свойств решений соответствующих уравне-
ний от входящих в них параметров и функций. Необходимость решения
этой проблемы обусловлена тем, что информация о характере протекания
исследуемого информационного, технологического или иного процесса
зачастую требуется уже в процессе создания соответствующей динами-
ческой системы.
Решение, преобразование и исследование уравнений, описывающих
динамические системы, осуществляется, естественно, определёнными
математическими методами. Изложение в сжатой форме этих методов и
составляет основное содержание данной книги. При этом предполагается,
что читатель имеет математическую подготовку в объёме двух первых
курсов технического вуза.
Одна из сторон освещаемой в книге проблемы состоит в том, что во
второй половине двадцатого века произошло довольно существенное
расширение математических методов исследования динамических сис-
тем, связанное с применением уравнений систем в переменных состоя-
ния. С другой стороны, не потеряли своей актуальности и эффективности
при решении многих задач и классические методы теории динамических
систем, базирующиеся на понятиях моделей вход-выход: передаточные
функции, частотные характеристики, дифференциальные уравнения вы-
сокого порядка. В связи с этим в книге большое внимание уделяется
взаимосвязи моделей динамических систем в переменных состояния и
моделей вход-выход.
В данную книгу не вошли методы исследования нелинейных дина-
мических систем. Это объясняется, с одной стороны, значительной слож-
ностью большинства из них, а с другой – узкой направленностью и соот-
ветственно, большим разнообразием этих методов, поскольку каждый из
них (за исключением, возможно, метода функций Ляпунова) пригоден
для исследования лишь определённого класса нелинейных динамических
систем.
В первой главе книги рассматриваются основные понятия и опреде-
ления теории динамических систем, в том числе понятие состояния; изла-
гается сущность системного подхода, основные формы математических
моделей как в переменных состояния, так и в форме вход-выход. Здесь
же показан аналитический метод получения математических моделей на
примере системы автоматического регулирования.
Во второй главе вводятся канонические формы уравнений динами-
ческих систем, и рассматриваются общие свойства решений обыкновен-
ных дифференциальных уравнений и их систем. Рассмотрение линейных
систем дифференциальных уравнений ограничивается формой Коши, как

6
наиболее часто встречающейся. Показано применение изложенных мето-
дов для определения реакции динамических систем на наиболее часто
используемые воздействия.
Третья глава посвящена изучению связей, существующих между
уравнениями динамических систем в переменных состояния и уравне-
ниями вход-выход. Материал этой главы весьма важен с точки зрения
того нового, что привнесло в теорию динамических систем введение по-
нятия состояния. Здесь же излагается метод решения полиномиальных
уравнений, которые используются при решении задач синтеза как линей-
ных, так и нелинейных динамических систем.
В четвёртой главе кратко освещаются математические методы опи-
сания случайных воздействий. Излагаются основы классического и со-
временного векторно-матричного подхода к исследованию динамических
систем, находящихся под влиянием случайных воздействий.
Математические модели дискретных динамических систем в форме
разностных уравнений и методы их исследования рассматриваются в пя-
той главе.
В приложении помещены важнейшие определения и соотношения
справочного характера теории числовых и функциональных матриц.
Ссылки на пункты приложений имеют вид П.Х.Х.
Данная книга является вторым изданием дополненной и существен-
но переработанной монографии [2]. Она предназначена для специали-
стов, занимающихся разработкой систем автоматического управления, а
также для студентов, магистрантов и аспирантов соответствующего про-
филя. Этим объясняется её существенный академический оттенок.
Автор считает своим приятным долгом выразить глубокую благо-
дарность всем своим близким, а также сотрудникам и коллегам по работе
за конкретную помощь в подготовке рукописи к печати.
Все замечания и предложения по книге будут с благодарностью
приняты. Просим направлять их по адресу: Кафедра САУ, ТРТУ, Некра-
совский 44, Таганрог ГСП-17А, 347928.
Автор

7
Г л а в а 1
МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИСТЕМ
§ 1.1. Основные понятия и определения
Понятие системы. Рассматриваемые в книге методы ориентирова-
ны на исследование систем, точнее, на исследование характера и свойств
их движений. Поэтому остановимся сначала на определении понятия
системы и её движений.
Сис те ма – это совокупность взаимодействующих, взаимосвязан-
ных элементов. Главное, чем интересуется теория систем, это движение
системы. При этом под д ви жени ями си сте мы понимаются любые
изменения её состояния.
Сос то яни е систе мы – это совокупность факторов, координат
или переменных, характеризующих однозначно и полно все движения
системы. Под состоянием системы можно понимать также память систе-
мы, то есть способность системы хранить информацию о собственном
поведении. В дальнейшем состояние системы, ее движения будут харак-
теризоваться совокупностью п ере ме нн ых с ос то ян ия. Число пере-
менных состояния, необходимых для полного и однозначного описания
состояния системы на всем временном интервале ее существования, на-
зывается по рядко м си ст емы и обозначается буквой n.
Таким образом, сис тема – это элементы, связи между ними и ее
состояние, отражающее движения системы. Элементы и связи между ни-
ми часто называются ст рукт ур ой си ст ем ы.
Примеры простейших систем приведены на рис. 1.1. На рис. 1.1,а
показана механическая динамическая система; ее состояние описывается
движением (скоростью и положением) шарика.
С в ет
q
a ) б )
в )
x
V
Рис. 1.1
8
На рис. 1.1,б приведена тоже механическая, но статическая система,
поскольку перемещения (прогиб, удлинение) балки очень малы. Наконец,
на рис. 1.1, в изображена электрическая схема еще одной динамической
системы. Движениями этой системы являются изменения токов в ветвях
цепи, напряжений на ее элементах, а также изменение интенсивности
светового потока, излучаемого электрической лампочкой. Эти величины
и могут, в частности, выступать в качестве переменных состояния, а их
совокупность может дать представление о состоянии этой электрической
системы.
Системы очень часто изображаются в виде бло к-с хе м, отобра-
жающих функциональное назначение элементов и связи между ними.
Такие блок-схемы называются функциональными схемами. Для примера,
на рис. 1.2 приведена функциональная схема изображенной на рис. 1.1,в
электрической цепи.
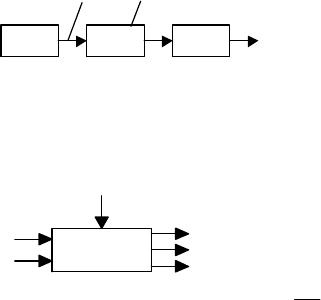
Аналогичным образом может изображаться и система в целом. На
рис. 1.3 приведено изображение системы общего вида.
Влияние на систему окружающей среды обычно отображается с по-
мощью вн еш ни х во зд ейс тви й (в ходн ых во здейс тви й). На рис. 1.3
это
1
g
,
2
g
и
1
f
. Воздействия могут быть векторными, например,
T
ggg ] [
21
=
. Это вектор-столбец входных воздействий.
Влияние системы на окружающую среду описывается вы ход ны ми
ве ли чи на ми (пер еме нн ыми )
системы. На рис. 1.3 это величи-
ны
3,2,1
yyy
. Они также могут
быть объединены в один вектор
T
yyyy ] [
321
=
– вектор вы-
ходных величин системы. Отметим, что
T
] [
– обозначение операции
транспонирования векторов или матриц (см. П.1.14).
Состояние системы на рис. 1.3
описывается вектором-столбцом
T
n
xxx ][
1
K=
, компонентами которо-
го являются переменные состояния,
i
x
,
ni ,1=
. Это вектор состояния системы.
Если состояние, например, системы, показанной на рис. 1.1,в, описывает-
ся переменными
R
ix
=
1
и
L
ix
=
2
, то порядок этой системы
2
=
n
.
E
q
Связи Элементы системы
LR ЭЛ
Рис. 1.2
g
1
g
2
y
1
y
2
y
3
f
1
x
Рис. 1.3
9
Любая динамическая система может находиться либо в установив-
шемся, либо в переходном режиме. Ус та но ви вш ийс я режи м систе-
мы – это режим, который может наблюдаться в системе сколь угодно
долго. Все другие режимы или состояния системы называются пер е-
хо дн ым и. Если в установившемся режиме, производные по времени
переменных системы равны нулю, то такой режим называется статиче-
ским.
Состояния системы, в которых скорость изменения переменных со-
стояния равна нулю, называются положениями равновесия системы. В
общем случае система может иметь несколько положений равновесия.
Если на блок-схеме обозначения элементов отображают функцио-
нальное назначение каждого элемента, то, как отмечалось выше, такая
блок-схема называется функциональной схемой. Если же элементы схе-
мы отражают математические преобразования своих входных перемен-
ных, то такая схема называется ст ру кту рной .
Выходная величина (переменная) системы или любого ее элемента в
теории систем рассматривается как р еа кц ия данного элемента на вход-
ную переменную. В общем случае в этой реакции учитываются преды-
дущие состояния этого элемента. Поэтому системы или элементы с вход-
ными переменными (воздействиями) являются как бы преобразователями
входной переменной в выходную. Элементы без входов называются и с-
точн ик ами или ген ера то рам и сигналов. Например, элемент Е на
рис. 1.2 является источником ЭДС. Входные воздействия и выходные
величины часто называются сигналами. При этом имеется в виду инфор-
мационная сторона этих величин.
Типы систем. Если число входных и выходных величин одинаково
и равно 1, то такая система называется од ном ер но й, при этом порядок
ее n может быть любым. На рис. 1.4 приведена блок-схема одномерной
системы.
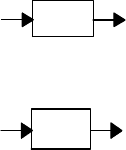
В обозначениях входных и выходных величин в этом случае индекс
обычно опускают, т.е. изображение одномер-
ной системы будет иметь вид, приведенный на
рис. 1.5.
Если же число входных или выходных
воздействий больше одного, то система назы-
вается м но го мер ной . На рис. 1.3 приведена
блок-схема многомерной системы.
Динамические и статические системы.
Если для описания системы необходимо учиты-
вать скорости изменения переменных, то система
является ди на мич еско й. Если этого не тре-
g
1
y
1
x
Рис. 1.4
g
y
Рис. 1.5
10
буется, то система является ст ати ческ ой или бе зы нерц ио нно й.
Стационарные и нестационарные системы. Величины, характери-
зующие, наряду с переменными, элемент или систему, называются их
па рам етр ами . Например, параметрами системы на рис. 1.1,в являются
значение индуктивности, сопротивление резистора, внутреннее сопро-
тивление источника ЭДС и электрической лампы.
В зависимости от характера параметров системы делятся на с та-
ци она рны е и не стац ио нар ные . Параметры с тац ио нар но й систе-
мы постоянны и не изменяются с течением времени. Параметры нес та -
ци она рной системы – это переменные величины, т.е. некоторые функ-
ции времени. Как правило, параметры системы изменяются намного мед-
леннее переменных состояния системы.
Непрерывные и дискретные системы. В н епр ер ыв ной системе
переменные определены во все моменты времени и могут принимать лю-
бые значения в некотором интервале. В д иск ретно й системе перемен-
ные определены лишь в некоторые моменты времени и принимают опре-
деленные дискретные значения. Например, в электрической схеме, при-
веденной на рис. 1.1,в, напряжение на катушке индуктивности L или ток
через резистор R определены в любой момент времени и могут прини-
мать любые (разумеется, ограниченные) значения, скажем, и 1, и 1,5, и –
1,557, т.е. все множество значений из интервала
[
]
MM
+
−
;
, где M – не-
которое число. Поэтому это непрерывная система.
Примером дискретной системы может служить обычный калькуля-
тор. На его восьмиразрядной шкале можно видеть числа, состоящие
только из восьми знаков цифр или нулей. Ввести в такой калькулятор
число из десяти или пятнадцати цифр нельзя. Другим признаком дис-
кретной системы является скачкообразное, обычно периодическое, изме-
нение значений переменных.
Детерминированные и стохастические системы. Д етер ми ни-
ро ван ные си стем ы – это системы с однозначно определенными пара-
метрами и структурой.
Сто ха сти чес ки е си ст емы – это системы, чьи параметры и
структура не определены однозначно, а могут принимать случайные зна-
чения или случайный вид.
Системный подход. Суть этого подхода, как показано на рис. 1.6,
заключается в том, что вместо изучения реальных систем, во всем их раз-
нообразии, изучаются математические модели этих систем.
Главным обоснованием целесообразности применения системного
подхода является тот факт, что мир, в котором мы живем, устроен так,
что движения реальных систем могут быть описаны (с приемлемой для
практики точностью) решениями некоторых математических уравнений.
