Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.


as
desired.
The
proof
of the
general
case
is
similar;
one
shows
that
the
Fourier coefficients
of
d
k
~
1
f/dx
k
~
1
are of
order
l/|n|,
the
Fourier
coefficients
of
d
k
~
2
f/dx
k
~
2
are of
Example
9.21.
1.
Define
f
:
(—1,1)
—>
R
by
f(x)
= x.
Then
f
per
has
jump
discontinuities
(at
x = (2k - 1), k = 0,
±1,±2,...),
and,
by
Theorem
9.20,
the
Fourier
coefficients
of f
must
be of
order
l/|ri|.
In
fact,
the
Fourier
coefficients
are
with
CQ
= 0.
2.
Define
f
:
(—1,1)
—>•
R
by
f(x)
=
x
2
.
Then
f
per
is
continuous,
but its
derivative
has
jump
discontinuities
(at x = (2k
—
1),
k = 0, ±1,
±2,...).
By
Theorem
9.20,
the
Fourier
coefficients
of f
must
be of
order
l/|n|
2
.
In
fact,
the
Fourier
coefficients
are
with
CQ
—
1/3.
3.
Define
f
:
(—1,1)
—>•
R by
f(x)
=
x
5
—2x
3
+x.
Then
f
per
and its
derivative
are
continuous,
but its
second derivative
has
jump discontinuities
(atx
=
(2k
—I),
438
Chapter
9.
More about Fourier
series
Since
f
per
is
continuous,
f
(—(.+)
=
/(^—),
and
e™
n
= e
I7rn
since
e
l9
is
27r-periodic.
Therefore,
we
obtain
where
d
n
,
n
= 0, ±1,
±2,...,
are the
Fourier
coefficients
of
df/dx.
By
Theorem
9.19,
we
have
s
*
\
and so
order
l/|n|
, and so
forth
to
obtain
the
desired result.
438
Chapter 9. More about Fourier series
Since jper
is
continuous,
j(
-£+)
=
j(£-),
and e
iTfn
=
e-
iTfn
since e
iIJ
is
27r-periodic.
Therefore,
we
obtain
C
n
=
__
z_
_(x)e-iTfnx/l
dx
.
Ie
dj
27m
-l
dx
--~d
-
n,
7rn
where d
n
, n =
0,
±I,
±2,
...
, are
the
Fourier coefficients of
dj
/dx.
By Theorem 9.19,
we
have
and so
as desired.
The proof of the general case
is
similar; one shows
that
the Fourier coefficients
of
d
k
-
1
j /dX
k
-
1
are of order
I/Inl,
the Fourier coefficients of d
k
-
2
j /dX
k
-
2
are of
order 1/lnI2, and so forth
to
obtain
the
desired result. 0
Example
9.21.
1.
Define f :
(-1,1)
-t
R
by
j(x)
=
x.
Then jper has
jump
discontinuities
(at x
= (2k - 1), k =
0,
±I,
±2,
..
.), and,
by
Theorem 9.20, the Fourier
coefficients
of
f
must
be
of
order
I/Inl.
In
fact, the Fourier coefficients are
with
Co
= 0.
i(-I)n
C
n
=
---,
n =
±1,±2,
...
,
7rn
2.
Define f :
(-1,1)
-t
R by
f(x)
= x
2
. Then
fper
is continuous, but its
derivative has
jump
discontinuities (at x = (2k - 1), k =
0,
±1,
±2,
..
.
J.
By
Theorem 9.20, the Fourier coefficients
of
f
must
be
of
order 1/lnI2.
In
fact,
the Fourier coefficients are
with
Co
= 1/3.
2(-I)n
C
n
= 2 2 ' n =
±I,
±2,
...
,
7rn
3.
Define f :
(-1,1)
-t
R by
f(x)
= x
5
-2x
3
+x.
Then fper and its derivative
are
continuous, but its second derivative has
jump
discontinuities (at x = (2k
-1),

with
CQ
=
8/15.
In
Figure
9.14
we
graph
the
error
in
approximating each
of
the
above
four functions
by
a
truncated Fourier series with
41
terms (the constant
term
and the 20
lowest
frequencies).
The
results
are as
expected;
as
f
per
gets
smoother,
the
convergence
of
the
Fourier series
to f
becomes more
rapid.
9.5.2 Uniform convergence
It now
follows immediately
that,
if
f
per
is
sufficiently
smooth,
then
its
Fourier series
converges uniformly
to /.
Theorem
9.22. Suppose
f
:
(—1,1)
—>
C is
continuous,
df/dx
is
piecewise
smooth,
and
f(—i)
=
f(l}.
Then
the
partial sums
of the
complex Fourier series
of
f
converge
uniformly
to f on
(—i,t)
(and
therefore
to
f
per
on
RJ.
Proof.
The
boundary conditions imply
that
f
per
is
continuous,
so by
Theorem
9.14,
we
know
that
the
Fourier series
of /
converges
point
wise
to
f
per
on R. We
must therefore show
that
the
convergence
is
uniform. Since
Therefore,
by
Theorem
9.20,
there
is a
constant
M
such
that
we
have
9.5.
Uniform
convergence
of
Fourier series
439
k — 0, ±1,
±2,...).
By
Theorem 9.20,
the
Fourier
coefficients
of f
must
be of
order
l/|n|
3
.
In
fact,
the
Fourier
coefficients
are
with
CQ
— 0.
4-
Define
f
:
(—1,1)
—>•
R by
f(x]
=
x
4
—
2x
2
+ 1.
Then
f
per
and its first two
derivatives
are
continuous,
but its
third derivative
has
jump discontinuities
(at
x — (2k —
1},
k =
0,±1,±2,...J.
By
Theorem 9.20,
the
Fourier
coefficients
of
f
must
be of
order l/\n
4
.
In
fact,
the
Fourier
coefficients
are
9.5. Uniform convergence
of
Fourier
series
439
k =
0,
±1, ±2, ..
.).
By
Theorem
9.20,
the Fourier coefficients
of
f
must
be
of
order 1/lnI3.
In
fact, the Fourier coefficients are
-8i(n
2
7f2
- 15)( _1)n
C
n
=
55
'
n=±1,±2,
...
,
7fn
with
Co
=
0.
4.
Define f :
(-1,
1)
~ R by
f(x)
=
X4
-
2X2
+
1.
Then
fper
and
its first two
derivatives are continuous, but
its
third derivative has
jump
discontinuities {at
x
= (2k -
1),
k = 0, ±1, ±2,
..
.).
By
Theorem
9.20,
the Fourier coefficients
of
f
must
be
of
order 1/lnI4.
In
fact, the Fourier coefficients are
-24(
-1)n
C
n
=
44'
n=±1,±2,
...
,
7fn
with
Co
= 8/15.
In
Figure 9.14 we graph the error
in
approximating each
of
the above
four
functions
by a truncated Fourier series with 41
terms
(the constant
term
and
the
20
lowest
frequencies). The results are as expected; as Iper gets smoother, the convergence
of
the Fourier series to 1 becomes more rapid.
9.5.2 Uniform
convergence
It
now follows immediately
that,
if
Iper is sufficiently smooth,
then
its Fourier series
converges uniformly
to
f.
Theorem
9.22.
Suppose f :
(-l,l)
~
C is continuous,
dfldx
is
piecewise
smooth,
and
f
(-l)
= 1 (l).
Then
the partial
sums
of
the complex Fourier series
01
f converge
uniformly
to 1 on
(-l,l)
(and therefore to Iper on
R).
Proof.
The
boundary conditions imply
that
Iper
is
continuous, so by Theorem
9.14,
we
know
that
the Fourier series of 1 converges pointwise
to
!per on
R.
We
must therefore show
that
the convergence is uniform. Since
00
fper(x) = L cnei1fnx/£,
n=-oo
we
have
N
-N-l
00
Iper(x) - L cnei1fnx/l = L cnei1fnx/£ + L cnei1fnx/£.
n=-N
n=-oo
n=N+l
Therefore, by Theorem 9.20, there is a constant M such
that
N
-N-l
00
Iper(x) - L cnei1fnx/£
L cnei1fnx/£ + L cnei1fnx/£
n=-N
n=-oo
n=N+l

440
Chapter
9.
More
about
Fourier
series
Figure
9.14.
The
errors
in
approximating each
function
from Example
9.21
by its
partial Fourier series with
41
terms:
f(x)
= x
(upper
left),
f(x)
= x
2
(upper
right),
f(x)
=
x
5
—
2x
3
+ x
(lower
left),
f(x]
=
x
4
-
2ar
2
+ 1
(lower right).
(using
the
fact
that
e
i7rnx/l
= 1).
This
holds
for all x € R, and so
Since
the
infinite series
440
Chapter 9. More about Fourier series
0.01
r--------------a
0.5
-0.01
-0.5
-1L------------~
-0.02
.......
------------"
-1
-0.5
o
X
0.5
10-
4
5~X--------------------__,
-1
-0.5
o
X
0.5 1
-5L-------------~
_2L------------~
-1
-0.5
o
X
0.5
-1
-0.5
o
X
0.5 1
Figure
9.14.
The errors
in
approximating each
function
from Example
9.21
by
its partial Fourier series with
41
terms:
f(x)
= x (upper left),
f(x)
= x
2
(upper right),
f(x)
= x
5
-
2x
3
+ x (lower left),
f(x)
= x4 -
2X2
+ 1 (lower right).
-N-l
00
:::;
2:
ICnei1rnx/il
+
2:
ICnei1rnx/ll
n=-oo
n=N+l
00
1
:::;
2M
2:
n
2
n=N+l
(using the fact
that
I e
i1rnx
/ i I = 1). This holds for all x E
R,
and
so
N
00
1
fper(x) -
2:
cnei7rnx/i
:::;
2M
2:
2"
for all x E
R.
n
n=-N
n=N+l
Since the infinite series
00
1
Ln
2
n=l

9.5.
Uniform
convergence
of
Fourier
series
441
is
convergent,
the
tail
of the
series tends
to
zero, which shows
that
tends
to
zero
at a
rate
that
is
independent
of x 6 R.
This proves
the
desired result.
As
with
pointwise
convergence,
the
uniform convergence
of
other
types
of
Fourier series
can be
deduced
from
their relationship
to the
complex Fourier series.
Corollary
9.23.
1.
Suppose
f
:
(—t,i]
—>•
R is
continuous
and
piecewise smooth,
df/dx
is
piece-
wise
smooth,
and
f(—£)
=
/(£)•
Then
the
full
Fourier series
of f
converges
uniformly
to f on
(—1,1)
(and
therefore
to
f
per
on
R,).
2.
Suppose
f
:
(0,^)
->
R is
continuous,
df/dx
is
piecewise smooth,
and
/(O)
=
f(i]
= 0.
Then
the
Fourier sine series
converges
uniformly
to f on
(—£,£}
(and
hence
to
f
0
dd,
the
periodic,
odd
extension
of
f, on all
ofH).
3.
Suppose
f
:
(0,£)
—>
R is
continuous
and
df/dx
is
piecewise smooth. Then
the
Fourier
cosine
series
converges
uniformly
to f on
(—i-,K)
(and hence
to
feven,
the
periodic, even extension
of
f, on all
ofH).
Proof.
1.
This
follows
immediately
from
the
equivalence
of the
full
Fourier series
and
the
complex Fourier series.
2.
This
follows
from
the
fact
that
the
sine series
of / is the
full
Fourier series
of
fodd
and
from
the
fact
that
the
continuity
of / and the
boundary conditions
/(O)
=
f(t]
= 0
guarantee
that
f
0
dd
is
continuous.
3.
This
follows
from
the
fact
that
the
cosine series
of / is the
full
Fourier series
of
feven
and
from
the
fact
that
the
continuity
of /
guarantees
that
Seven
is
continuous.
The
special
property
of the
cosine series
is
important;
no
boundary conditions
must
be
satisfied
in
order
for the
convergence
to be
uniform.
Indeed,
the
relevant
boundary conditions
for a
cosine series
are
Neumann conditions, which involve
df/dx.
The
Fourier cosine
coefficients
of / are O
(l/|n|
3
)
or O
(l/|n|
2
)
according
to
whether
/
satisfies
or
does
not
satisfy
homogeneous Neumann conditions (see
Exercise
4), but in
either case,
the
Fourier series converges
uniformly
to /.
Example
9.24.
Let f
:
[0,1]
—>
R be
defined
by
f(x)
=
x
2
.
Since
f
does
not
satisfy
the
Dirichlet conditions,
the
sine series
does
not
converge
uniformly
on
[0,1].
9.5. Uniform convergence
of
Fourier
series
is
convergent, the tail of the series tends to zero, which shows
that
N
fper(x) - L cnei'lmxll
n=-N
441
tends
to
zero
at
a
rate
that
is
independent of x E
R.
This proves
the
desired result.
D
As
with pointwise convergence, the uniform convergence of other types of
Fourier series can be deduced from their relationship
to
the
complex Fourier series.
Corollary
9.23.
1.
Suppose f : (-I!.,
I!.)
-+
R is continuous and piecewise smooth,
elf
/ dx is piece-
wise smooth, and
f(
-I!.)
=
f(I!.).
Then the full Fourier series
of
f converges
uniformly to f
on
(-I!.,I!.)
(and therefore to
fper
on
R).
2.
Suppose f :
(O,I!.)
-+
R
is
continuous,
df/dx
is piecewise smooth, and f(O) =
f(l!.)
=
O.
Then the Fourier sine series converges uniformly
to
f on (-I!.,
I!.)
(and hence to
fodd,
the periodic,
odd
extension of
f,
on all
ofR).
3.
Suppose f :
(0,
I!.)
-+
R
is
continuous and
df/
dx
is
piecewise smooth. Then
the Fourier cosine series converges uniformly to f on (-I!.,
I!.)
(and hence to
feven, the periodic, even extension
of
f,
on all
of
R).
Proof·
1.
This follows immediately from the equivalence of the full Fourier series
and
the complex Fourier series.
2.
This follows from
the
fact
that
the
sine series of f
is
the
full Fourier series of
fodd
and from the fact
that
the continuity of f and the boundary conditions
f(O)
=
f(l!.)
= a guarantee
that
fodd
is
continuous.
3.
This follows from the fact
that
the
cosine series of f
is
the full Fourier series
of
feven
and from the fact
that
the continuity of f guarantees
that
feven
is
continuous.
D
The special property of the cosine series
is
important; no boundary conditions
must be satisfied in order for the convergence
to
be uniform. Indeed, the relevant
boundary conditions for a cosine series are Neumann conditions, which involve
df
/dx.
The Fourier cosine coefficients of f are 0
(1/lnI3)
or 0
(1/lnI2)
according
to whether
f satisfies or does not satisfy homogeneous Neumann conditions (see
Exercise 4),
but
in either case, the Fourier series converges uniformly
to
f.
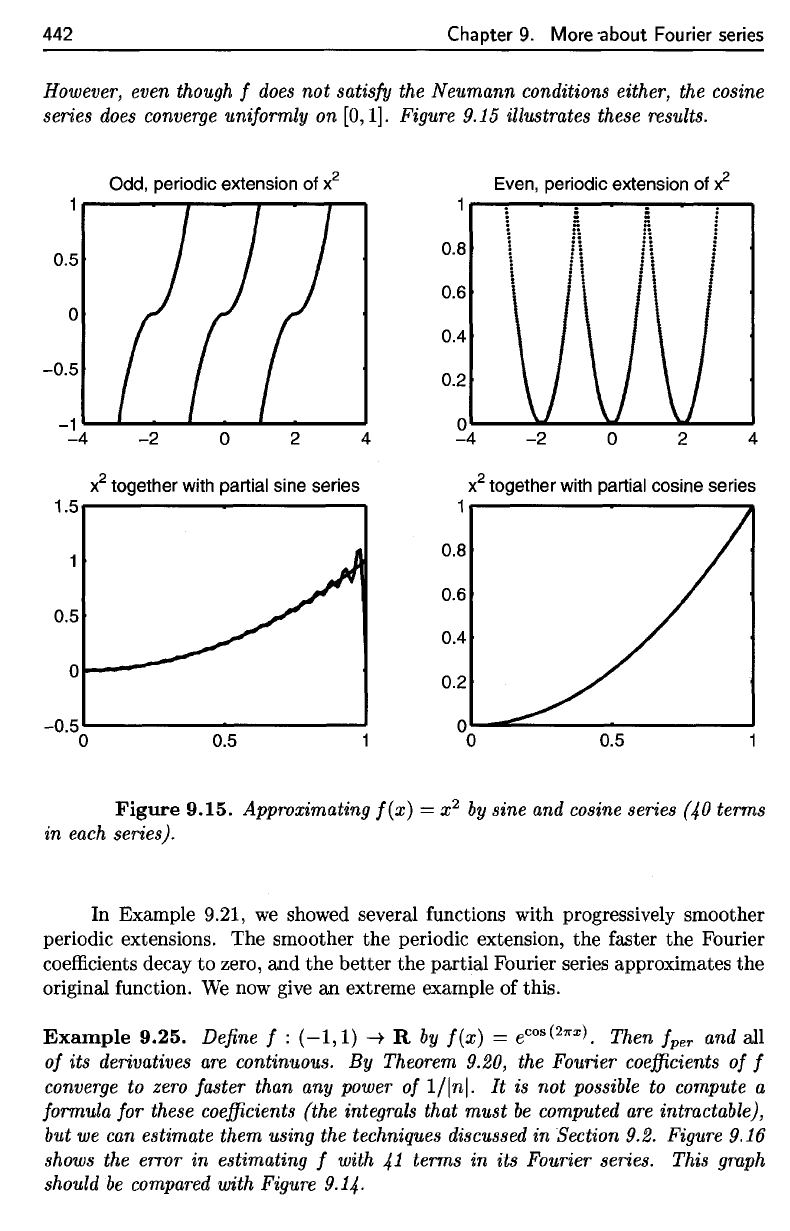
Example
9.24.
Let f :
[0,1]
-+
R
be
defined
by
f(x)
= x
2
•
Since f
does
not
satisfy the Dirichlet conditions, the sine series
does
not converge uniformly on
[0,
1].
442
Chapter
9.
More-about
Fourier
series
However, even though
f
does
not
satisfy
the
Neumann
conditions either,
the
cosine
series
does
converge
uniformly
on
[0,1].
Figure 9.15 illustrates these results.
Figure
9.15. Approximating
f(x)
—
x
2
by
sine
and
cosine series
(40
terms
in
each series).
In
Example
9.21,
we
showed several functions with progressively smoother
periodic
extensions.
The
smoother
the
periodic extension,
the
faster
the
Fourier
coefficients
decay
to
zero,
and the
better
the
partial
Fourier
series
approximates
the
original function.
We now
give
an
extreme
example
of
this.
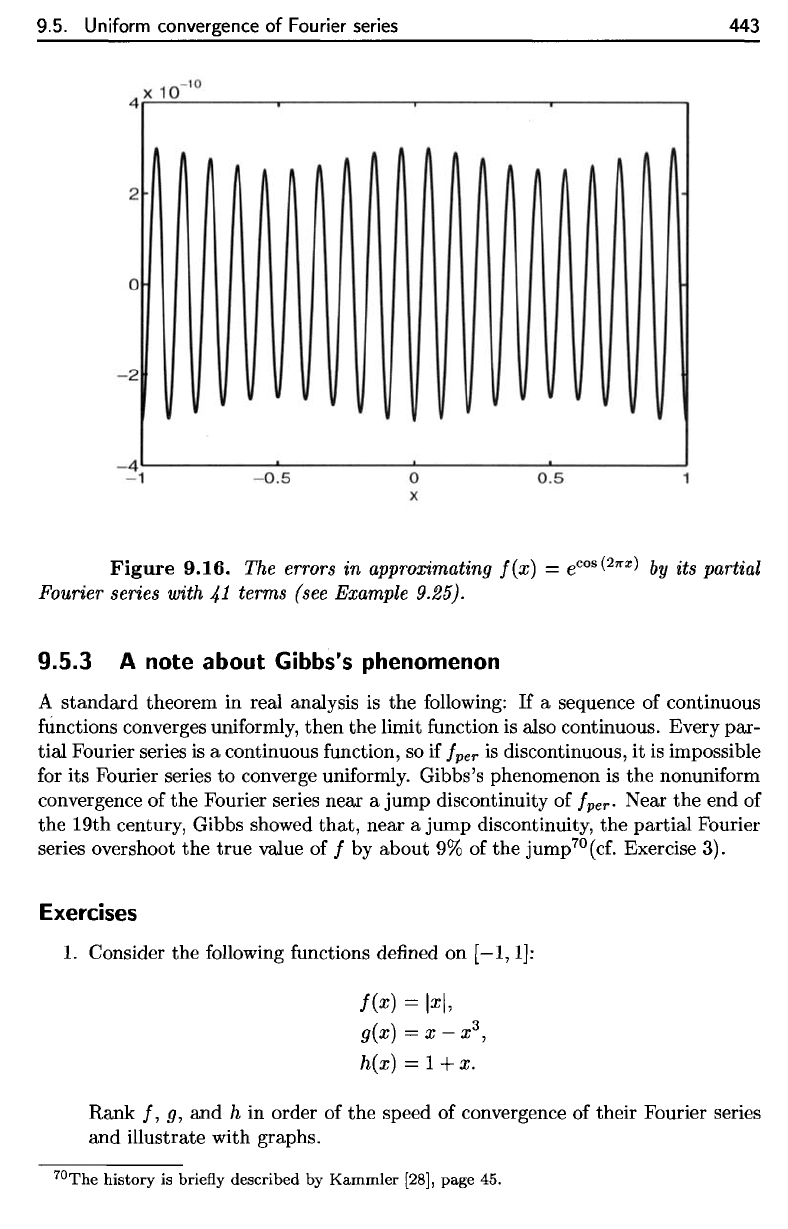
Example
9.25.
Define
f
:
(-1,1)
-»•
R by
f(x)
=
e
cos
(
27ra;
).
Then
f
per
and all
of
its
derivatives
are
continuous.
By
Theorem 9.20,
the
Fourier
coefficients
of f
converge
to
zero faster than
any
power
of
l/\n\.
It is not
possible
to
compute
a
formula
for
these
coefficients
(the integrals that must
be
computed
are
intractable),
but
we can
estimate
them
using
the
techniques discussed
in
Section 9.2. Figure 9.16
shows
the
error
in
estimating
f
with
41
terms
in its
Fourier series. This
graph
should
be
compared
with Figure
9.14-
442
Chapter
9.
More 'about Fourier
series
However, even though f does
not
satisfy the
Neumann
conditions either, the cosine
series does converge uniformly on
[0,1]. Figure 9.15 illustrates these results.
Odd, periodic extension of x
2
0.5
0
-0.5
-1
-4
-2
0
2 4
x
2
together with partial sine series
1.Sr-----------~
0.5
0
-0.5
0 0.5
0.8
0.6
0.4
0.2
Even, periodic extension
of;
=
:!
1\
i i
fi
1\
:
:
I
o~-~~-~--~-~
-4
-2
o 2 4
x
2
together with partial cosine series
1~--------------------~
0.8
0.6
0.4
0.2
0
0
0.5
Figure
9.15.
Approximating
f(x)
= x
2
by
sine and cosine series (40 terms
in
each series).
In Example 9.21,
we
showed several functions with progressively smoother
periodic extensions. The smoother the periodic extension, the faster the Fourier
coefficients decay
to
zero, and
the
better
the partial Fourier series approximates
the
original function.
We
now give an extreme example of this.
Example
9.25.
Define
f:
(-1,1)
-t
R by
f(x)
= e
cos
(21rJ;). Then
fper
and all
of
its derivatives are continuous.
By
Theorem 9.20, the Fourier coefficients
of
f
converge to zero faster than any power
of
l/lnl.
It
is
not
possible to compute a
formula for these coefficients (the integrals that
must
be
computed are intractable),
but
we
can estimate them using the techniques discussed
in
Section 9.2. Figure 9.16
shows the error
in
estimating f with
41
terms
in
its Fourier series. This graph
should
be
compared with Figure 9.14.
9.5.
Uniform
convergence
of
Fourier series
443
Figure
9.16.
The
errors
in
approximating
f(x)
=
e
cos
(
27ra;
)
by
its
partial
Fourier
series with
41
terms (see Example 9.25).
9.5.3
A
note
about
Gibbs's
phenomenon
A
standard
theorem
in
real analysis
is the
following:
If a
sequence
of
continuous
functions
converges
uniformly,
then
the
limit
function
is
also continuous. Every par-
tial
Fourier series
is a
continuous function,
so if
f
per
is
discontinuous,
it is
impossible
for
its
Fourier series
to
converge uniformly. Gibbs's phenomenon
is the
nonuniform
convergence
of the
Fourier series near
a
jump discontinuity
of
f
per
.
Near
the end of
the
19th century, Gibbs showed
that,
near
a
jump discontinuity,
the
partial
Fourier
series overshoot
the
true value
of / by
about
9% of the
jump
70
(cf.
Exercise
3).
70
The
history
is
briefly
described
by
Kammler
[28],
page
45.
Exercises
1.
Consider
the
following functions defined
on
[—1,1]:
Rank
/,
g,
and
h
in
order
of the
speed
of
convergence
of
their Fourier series
and
illustrate with
eraohs.
9.S.
Uniform convergence
of
Fourier
series
2
o
- 2
- 1
- 0.5
o
x
0.5
443
Figure
9.16. The errors in approximating
f(x)
= e
cos
(27rx)
by
its partial
Fourier series with
41
terms
(see
Example 9.25).
9.5.3 A note about Gibbs's phenomenon
A
standard
theorem in real analysis
is
the following:
If
a sequence
of
continuous
functions converges uniformly,
then
the limit function
is
also continuous. Every par-
tial Fourier series
is
a continuous function, so if
fper
is
discontinuous,
it
is
impossible
for its Fourier series
to
converge uniformly. Gibbs's phenomenon
is
the nonuniform
convergence of
the
Fourier series near a
jump
discontinuity of
fper.
Near
the
end of
the 19th century, Gibbs showed
that,
near a
jump
discontinuity,
the
partial Fourier
series overshoot
the
true
value of f by about
9%
of the jump
70(cf.
Exercise 3).
Exercises
1. Consider
the
following functions defined on
[-1,1]:
f(x)
=
lxi,
g(x) = x - x
3
,
h(x)=l+x.
Rank f, g, and h in order of the speed of convergence of their Fourier series
and illustrate with graphs.
70
The
history
is briefly described
by
Kammler
[28], page 45.

444
Chapter
9.
More about Fourier
series
2.
Find
an
example
of a
function
/ :
[—1,1]
—>•
R
whose Fourier
coefficients
are
but
not
(Hint:
Choose
/ to be a
fifth-degree
polynomial.)
3.
Consider
the
function
/ :
[—
1,1]
—>•
R
defined
by
Verify
numerically
that
the
overshoot
in
Gibbs's phenomenon
is
about
9% of
the
jump
at x = 0.
4.
Suppose
/ :
(0,^)
->
R is
continuous
and
df/dx
is
piecewise smooth.
(a)
Prove
that
the
periodic, even extension
of / is
continuous
and
therefore
that
the
Fourier cosine
coefficients
of / are O
(l/|n|
2
).
(b)
Prove
that
the
Fourier cosine
coefficients
of / are 0
(l/|n|
3
)
if and
only
if
9.6
Mean-square convergence
of
Fourier
series
We
now
wish
to
show
that,
for a
large class
of
functions
/ :
(—1,1)
—>
C, the
complex Fourier series
of /,
converges
to / in the
mean-square sense. Mean-square convergence means
that
if
we
write
then
In
contrast
to
pointwise
or
uniform
convergence,
it
turns
out
that
the
mildest
as-
sumption
about
/
guarantees mean-square convergence
of the
Fourier series.
In
order
to
discuss mean-square convergence,
it had
better
be the
case
that
/
has a finite L
2
norm:
a
444
Chapter
9.
More about Fourier
series
2.
Find
an example of a function
f:
[-1,1]
-+
R whose Fourier coefficients are
o
C:14)
but
not
o
C:15).
(Hint: Choose f
to
be a fifth-degree polynomial.)
3.
Consider
the
function f : [-1,1]
-+
R defined by
f(x)
= {O, -1::; x <
0,
1,
0::; x
::;
1.
Verify numerically
that
the
overshoot in Gibbs's phenomenon
is
about
9%
of
the
jump
at
x =
O.
4.
Suppose f :
(0,
£)
-+
R is continuous and df / dx is piecewise smooth.
(a) Prove
that
the periodic, even extension of f
is
continuous
and
therefore
that
the
Fourier cosine coefficients of
fare
0
(1/lnI2).
(b) Prove
that
the
Fourier cosine coefficients of f are 0
(1/lnI3)
if
and
only
if
!
(0)
= !
(£)
=
O.
9.6 Mean-square convergence
of
Fourier
series
We
now wish
to
show
that,
for a large class of functions f :
(-£,
£)
-+
C,
the
complex Fourier series of
I,
n=-oo
converges
to
f in
the
mean-square sense. Mean-square convergence means
that
if
we
write
N
IN(X) = L
cnei1rnx/f,
n=-N
then
III
-
INII£2
-+ 0 as N -+
00.
In contrast
to
pointwise or uniform convergence,
it
turns
out
that
the
mildest as-
sumption about
I guarantees mean-square convergence of
the
Fourier series.
In
order
to
discuss mean-square convergence,
it
had
better
be
the
case
that
I
has a finite £2 norm:
IIIII
=
iff
I/(xW
dx <
00.

must
be
positive.
9.6. Mean-square convergence
of
Fourier series
445
It
turns
out
that
this essential assumption
is the
only assumption required
to
guar-
antee
the
convergence
of the
Fourier series
to / in the
mean-square sense.
To
justify
this
statement,
we
must begin with some technical preliminaries.
The
technicalities
are
sufficiently
subtle
as to be
beyond
the
scope
of
this
book—the
reader
will
have
to
accept certain assertions
on
faith.
9.6.1
The
space
L
2
(-t,£)
We
wish
to
identify
the
space
of all
functions
/ :
(—(.,
i]
—)•
C
such
that
the
complex
Fourier series
of /
converges
to / in the
mean-square sense. Accepting
the
truth
of
the
statement
in the
previous paragraph,
it
would
be
natural
to
define
There
is
more
to
this definition
than
meets
the
eye, however.
First
of
all,
one of the
essential properties
of a
norm
is the
following:
When
/ is a
function,
/ = 0
means
that
/ is the
zero function:
f(x)
— 0 for all
x
e
(—1,1).
As
long
as we
restrict ourselves
to
continuous functions,
(9.23)
holds.
71
However,
a
discontinuous function
can be
nonzero
and yet
have
I/
2
norm equal
to
zero.
For
example, consider
the
function
/ :
(—1,1)
->
R
defined
by
This function
is not the
zero
function,
but
since
the
integrand
is
zero everywhere except
a
single point. Therefore,
in
order
for
(9.23)
to be
satisfied,
we
have
to
agree
that
/ and g are
regarded
as the
same
function
provided
We
will
have more
to say
about this below.
There
is
another
difficulty
with
(9.22).
Since
our
interest
is
mean-square
convergence
of
functions,
the
following
property
is
desirable:
If
{/N}
is a
sequence
71
If
/ is
continuous
and not the
zero
function,
then,
by
continuity, there must exist
an
interval
(a,
6) C
(—1,1)
on
which
/ is
nonzero,
and so
9.6. Mean-square convergence
of
Fourier
series
445
It
turns out
that
this essential assumption
is
the only assumption required to guar-
antee the convergence of
the
Fourier series
to
f in the mean-square sense.
To
justify
this statement,
we
must begin with some technical preliminaries. The technicalities
are sufficiently subtle as to be beyond the scope of this
book~the
reader will have
to accept certain assertions on faith.
9.6.1 The space L2(
-.e,.e)
We
wish to identify the space of all functions f :
(-i,
i)
-+ C such
that
the complex
Fourier series of
f converges
to
f in the mean-square sense. Accepting
the
truth
of
the
statement in the previous paragraph, it would be natural
to
define
L2(_£,£) =
{f:
(-i,i)
-+ C :
f~l
If(x)j2dx <
oo}.
(9.22)
There
is
more to this definition
than
meets the eye, however.
First of all, one of
the
essential properties of a norm
is
the
following:
11/11=0=*1=0.
(9.23)
When
1
is
a function, 1 = 0 means
that
1
is
the
zero function: I(x) = 0 for all
x E
(-i,
i).
As
long as
we
restrict ourselves
to
continuous functions, (9.23)
holds.71
However, a discontinuous function can be nonzero and yet have
L2
norm equal to
zero. For example, consider the function
1 :
(-1,
1)
-+ R defined by
I(x) = '
{
Ix
= 0,
0,
x
I:-
O.
This function
is
not
the
zero function,
but
since
the
integrand
is
zero everywhere except a single point. Therefore, in order
for (9.23) to be satisfied,
we
have to agree
that
1 and 9 are regarded as the same
function provided
ill
If(x) - g(x)j2 dx =
O.
We
will have more to say about this below.
There
is
another difficulty with (9.22). Since our interest
is
mean-square
convergence of functions,
the
following property
is
desirable:
If
UN}
is
a sequence
71
If
f is continuous
and
not
the
zero function,
then,
by
continuity,
there
must
exist
an
interval
(a,
b)
C
(-t,
t)
on
which f is nonzero,
and
so
i:
If(x)1
2
dx
~
lb
If(x)1
2
dx
must
be positive.

446
Chapter
9.
More about Fourier series
of
functions
in
L
2
(—l,l)
and
/AT
—>•
/ in the
mean-square sense, then
/ 6
L
2
(—£,l).
Is
this property satisfied
by
L?(-t,
t)
as
defined
by
(9.22)?
The
answer
is, it
depends
on
the
definition
of the
integral used
in
(9.22).
For
example,
any
function with
an
infinite
singularity
fails
to be
Riemann integrable;
as an
example, consider
the
function
/ :
[—
1,1]
—>•
R
defined
by
This
function
is not
Riemann integrable
on
(—1,1)
because
of the
infinite
disconti-
nuity
at x = 0.
However,
\f(x}\
2
has a finite
area
under
its
graph,
as the
following
calculation
shows:
Therefore,
we
would like
to
include
/ in
L
2
(—1,1),
which means
that
we
must
interpret
the
integral
as an
improper Riemann integral when
/ has a finite
number
of
singularities.
However,
allowing improper Riemann integrals
is not
enough, since
it is
pos-
sible
to
construct
a
sequence
{/N}
with
the
following
properties:
1.
/jv
has N
infinite
discontinuities;
2.
/TV
is
square-integrable when
the
integral
is
interpreted
as an
improper Rie-
mann integral;
3.
{/AT}
converges
in the
mean-square sense
to a
function
with
an
infinite
number
of
discontinuities.
A
function
with
an
infinite
number
of
discontinuities cannot
be
Riemann integrable,
even
in the
improper sense.
Faced with these
difficulties,
mathematicians eventually concluded
that
a
bet-
ter
notion
of
integration
was
needed, which
was
created
by
Henri Lebesgue (the
"L"
in
L
2
).
The
definition
of the
Lebesgue integral
is
beyond
the
scope
of
this
book,
but we can
describe
its
important features.
The
theory begins with
a
measure
for
subsets
of R
that
agrees with
our
intuition
for
simple sets (for example,
the
measure
of
an
interval
[a,
b]
is b
—
a).
The
Lebesgue measure
is
defined
in a
consistent fashion
even
for
very
complicated
subsets
of R, but not for all
subsets.
Sets
whose Lebesgue
measure
is
defined
are
called (Lebesgue) measurable.
Any set
with measure zero
is
then neglible
in a
certain sense. Every
set
containing
a finite
number
of
points
has
measure
zero.
72
The
Lebesgue
integral
is
defined
for
functions
that
are
measurable;
the
prop-
erty
of
measurability
is a
regularity property like continuity
or
differentiability,
but
72
Some sets having
an
infinite
number
of
points also have measure zero.
A
countable
set (a
set
that
can be put in
one-to-one correspondence with
the
integers
1,2,3,...)
has
measure zero.
For
example,
the set of all
rational numbers
has
measure zero. Some uncountable sets also have
measure zero, although, obviously, such
a set
occupies
a
neglible part
of the
real line.
446
Chapter
9.
More about Fourier
series
offunctions in
L2
(
-f,
f)
and
IN
--+
I in
the
mean-square sense, then I E
L2
(
-f,
f).
Is this property satisfied by
L2(
-f,
f)
a.s
defined by (9.22)? The answer is, it depends
on
the
definition of the integral used in (9.22). For example, any function with
an
infinite singularity fails
to
be Riemann integrable;
a.s
an example, consider the
function
I :
[-1,
1]
--+
R defined by
1
I(x)
=
IxI
1
/
4
'
This function
is
not Riemann integrable on
(-1,1)
because of the infinite disconti-
nuityat
x =
O.
However,
I/(x)12
has a finite area under its graph,
a.s
the following
calculation shows:
lim {
r-€
I/(xW
dx
+
/1
I/(xW
dX}
= lim 4(1 -
-IE)
=
4.
€---+o+
1-1
f
f---+O+
Therefore,
we
would like
to
include I in
L2
(
-1,
1),
which means
that
we
must
interpret
the
integral
a.s
an improper Riemann integral when I has a finite number
of singularities.
However, allowing improper Riemann integrals
is
not enough, since it
is
pos-
sible
to
construct a sequence
{IN}
with
the
following properties:
1.
IN
has N infinite discontinuities;
2.
IN
is square-integrable when the integral
is
interpreted as
an
improper Rie-
mann integral;
3.
{IN}
converges in
the
mean-square sense to a function with an infinite number
of discontinuities.
A function with an infinite number of discontinuities cannot be Riemann integrable,
even in
the
improper sense.
Faced with these difficulties, mathematicians eventually concluded
that
a bet-
ter
notion of integration was needed, which was created by Henri Lebesgue (the
"L"
in L2). The definition of the Lebesgue integral
is
beyond
the
scope of this book,
but
we
can describe its important features. The theory begins with a measure for
subsets of
R
that
agrees with our intuition for simple sets (for example, the mea.sure
of
an
interval
[a,
b]
is
b-a).
The Lebesgue mea.sure
is
defined in a consistent
fa.shion
even for very complicated subsets of
R,
but
not
for all subsets. Sets whose Lebesgue
mea.sure
is
defined are called (Lebesgue) measurable. Any set with mea.sure zero
is
then neglible in a certain sense. Every set containing a finite number of points
ha.s
mea.sure
zero.72
The Lebesgue integral
is
defined for functions
that
are
measurable;
the
prop-
erty of measurability
is
a regularity property like continuity or differentiability,
but
72Some sets having
an
infinite
number
of
points
also have measure zero. A countable set
(a
set
that
can
be
put
in one-to-one correspondence
with
the
integers
1,2,3,
...
) has measure zero.
For
example,
the
set
of
all
rational
numbers
has measure zero. Some uncountable sets also have
measure zero, although, obviously, such a
set
occupies a neglible
part
of
the
real line.

9.6. Mean-square convergence
of
Fourier
series
447
much
weaker—functions
with
an
infinite
number
of
discontinuities
can be
mea-
surable,
for
example.
We
cannot
give
the
precise definitions
of
these
concepts—
measurable set, measurable function, Lebesgue
integral—in
this
text.
The
defini-
tions, however, have
the
following
consequences:
1.
Two
measurable functions
/ and a
satisfy
if
and
only
if / and g
differ
only
on a set of
measure zero.
It is in
this sense
that
a set of
measure
zero
is
negligible: functions
differing
only
on a set of
measure zero
are
regarded
as
being
the
same.
2.
If / is
Riemann integrable, then
it is
Lebesgue integrable,
and the two
integrals
have
the
same value.
This
last
property assures
us
that
whenever
we are
dealing with
a
continuous
or
piecewise
continuous function,
we can
compute
its
integral using
the
familiar tech-
niques
of
caculus.
On the
other hand,
the
Lebesgue integral
is
sufficiently
powerful
to
handle pathological cases
that
arise inevitably when mean-square convergence
is
studied.
We
will
discuss other properties
of
Lebesgue integration
and
L
2
(—£,(.)
below.
We
can now
define
L
2
(—l,l)
more precisely
as the set of all
measurable
func-
tions
/ :
(—t,K)
—>
C
satisfying
with
the
understanding
that
two
functions
that
differ
only
on a set of
measure zero
represent
the
same element
of the
space.
In
order
to
understand
the L
2
theory
of
Fourier series,
we
need
two
more facts
about
L
2
(—l.,l},
facts
that
we
cannot prove here,
as
their development would
take
us
too far
astray.
Even stating
the
second fact takes
a
certain amount
of
work.
The first
fact, Theorem 9.26, allows
us to
prove
that
the
Fourier series
of
every
L
2
function
converges
to the
function
in the
mean-square sense.
Theorem
9.26.
Let f
e
L
2
(—l,l),
and let e be any
positive
real
number
(no
matter
how
small). Then there
is an
infinitely
differentiate
function
g
:
[—•£,•£]
—>•
C
such
that
Moreover,
g can be
chosen
to
satisfy
g(—t]
=
g(i]
= 0.
This theorem simply says
that
any
L
2
(—t,
(,}
function
can be
approximated
ar-
bitrarily well,
in the
mean-square sense, using
a
smooth
function
satisfying Dirichlet
conditions.
9.6. Mean-square convergence
of
Fourier
series
447
much
weaker-functions
with
an
infinite number of discontinuities can be mea-
surable, for example.
We
cannot give
the
precise definitions of these
concepts-
measurable set, measurable function, Lebesgue
integral-in
this text.
The
defini-
tions, however, have
the
following consequences:
1. Two measurable functions f
and
9 satisfy
if
and
only
if
f
and
9 differ only on a set of measure zero.
It
is in this sense
that
a set of measure zero is negligible: functions differing only on a set of
measure zero are regarded as being
the
same.
2.
If
f is Riemann integrable,
then
it
is
Lebesgue integrable,
and
the
two integrals
have
the
same value.
This last property assures us
that
whenever
we
are dealing with a continuous or
piecewise continuous function,
we
can compute its integral using
the
familiar tech-
niques of caculus.
On
the other hand,
the
Lebesgue integral is sufficiently powerful
to
handle pathological cases
that
arise inevitably when mean-square convergence
is
studied.
We
will discuss
other
properties of Lebesgue integration
and
L2
(
-f,
f)
below.
We
can now define
L2
(
-f,
f)
more precisely as
the
set of all measurable func-
tions
f :
(-£,
f)
--t C satisfying
with
the
understanding
that
two functions
that
differ only on a set of measure zero
represent the same element of
the
space.
In order
to
understand
the
L2
theory of Fourier series,
we
need two more facts
about
L2
(
-f,
f),
facts
that
we
cannot prove here, as their development would take
us
too
far astray. Even stating
the
second fact takes a certain amount of work.
The
first fact, Theorem 9.26, allows us
to
prove
that
the
Fourier series of every
L2
function converges
to
the
function in
the
mean-square sense.
Theorem
9.26.
Let f E L2(
-£,
e),
and let E
be
any positive real number (no
matter
how small). Then there is an infinitely differentiable function 9 : [-£,
£]
--t
C such
that
Ilf -
gll£2
< E.
Moreover, 9 can
be
chosen to satisfy
g(
-f)
= g(f) =
O.
This theorem simply says
that
any
L2
(
-£,
£)
function can be approximated ar-
bitrarily well, in
the
mean-square sense, using a smooth function satisfying Dirichlet
conditions.
