Грехов В.П., Зарицкий М.Н., Ключникова Г.А., Куприков А.В. Теория автоматического управления
Подождите немного. Документ загружается.

Для устойчивости системы четвертого порядка с характеристическим уравнением
0
01
2
2
3
3
4
4
apapapapa
(4.15)
кроме положительности всех коэффициентов требуется выполнение условия
0
2
3
2
141233
aaaaaaa
> 0. (4.16)
Нетрудно доказать, что при положительности всех коэффициентов условие (4.16)
обеспечивает выполнение необходимого неравенства
2
> 0.
Таким образом,
для устойчивости систем не выше четвертого порядка необходимо и достаточно, чтобы
все коэффициенты характеристического уравнения и определитель
1n
были
положительными.
Критерий Гурвица целесообразно применять для анализа устойчивости систем не выше
пятого порядка. При n>5 достаточные условия устойчивости усложняются, а вычисления
определителей становится громоздким.
Пример 4.1. Определим с помощью критерия Гурвица устойчивость САУ при следующих
значениях параметров:
T
Я
= 0,15 c; T
M
= 1 c; T
П
= 0,01 c; K
Σ
= 15.
Характеристическое уравнение системы
(T
П
p + 1)( T
Я
T
M
p
2
+ T
M
p + 1) + K
Σ
= 0,
или
a p a p a p a
3
3
2
2
1 0
0
,
где a
3
= T
П
T
Я
T
M
= 0.01
1
0,15 = 0,0015 c
3
;
a
2
= T
Я
T
M
+ T
П
T
M
= 1
0,15+ 1
0,01 = 0,16 c
2
;
a
1
= T
M
+ T
П
= 1 + 0,01 = 1,01 c;
a
0
= 1+15 = 16.
Все коэффициенты характеристического уравнения положительны, т.е. необходимое
условие устойчивости выполняется. Проверим выполнение достаточного условия, для чего
вычислим определитель
2
= a
1
a
2
- a
3
a
0
= 1,01
0,16 - 0,0015
16 = 0,1616 - 0,0224 = +0,1376,
2
> 0, следовательно, система устойчива.
Решим теперь обратную задачу: определим, какое максимальное значение суммарного
коэффициента усиления К
допустимо по условию устойчивости.
Максимальное допустимое значение К определяется из условия нахождения системы на
границе колебательной устойчивости. Это значение К называют критическим или граничным
39
2
= a
1
a
2
- a
3
a
0кр
= 0,
отсюда a
0кр
= a
1
a
2
/a
3
= 1,01
0,16/0,0015 = 107,73.
К
кр
= a
0кр
- 1 = 107,73 - 1= 106,73.
Следовательно, рассмотренная в примере система устойчива, если К < К
кр.
4.3. Частотный критерий устойчивости Найквиста
В некоторых учебниках и учебных пособиях этот критерий именуется критерием
Найквиста - Михайлова. Это объясняется тем, что этот критерий был предложен американским
ученым Х. Найквистом для анализа устойчивости усилителей с обратной связью. Позднее А.В.
Михайлов доказал возможность его применения для анализа устойчивости линейных САУ.
Основная особенность и практическая ценность этого критерия заключается в том, что
анализ устойчивости замкнутой системы выполняется по частотным характеристикам
разомкнутого контура регулирования.
Рассматриваются три случая анализа устойчивости: 1) система в разомкнутом состоянии
устойчива; 2) система в разомкнутом состоянии неустойчива; 3) система в разомкнутом
состоянии нейтрально устойчива (нулевые корни в характеристическом уравнении
разомкнутой системы, что возможно при наличии в контуре регулирования интегрирующих
звеньев).
Рассмотрим анализ устойчивости замкнутой системы для случая, когда эта система
устойчива в разомкнутом состоянии. Для этого случая дадим физическое объяснение и
доказательство. Поэтому уместно поставить вопрос: почему система, устойчивая в
разомкнутом состоянии, может оказаться неустойчивой в замкнутом состоянии?
Целесообразно проанализировать преобразование в контуре регулирования отдельных
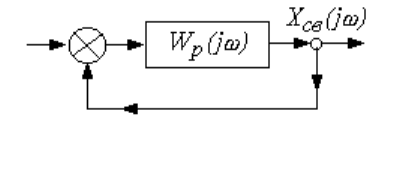
составляющих сигнала на выходе (рис. 4.2)
Допустим, на частоте
argW
p
(j
)=-180
.
Следовательно, на этой частоте отрицательная
обратная связь превращается в положительную.
При этом возможны три варианта:
Рис.4.2
40
1) Модуль частотной передаточной функции разомкнутой системы на частоте
W
p
(j
)
<1, что ведет к затуханию колебаний сигнала на этой частоте в замкнутом контуре, а
это свидетельствует об устойчивости такой системы.
2)
W
p
(j
)
=1, что свидетельствует о возникновении незатухающих колебаний с
частотой
, т.е. замкнутая система находится на колебательной границе устойчивости
(частота незатухающих колебаний
).
3)
W
p
(j
)
>1, что ведет к увеличению амплитуды колебаний на частоте
и,
следовательно, такая система неустойчива.
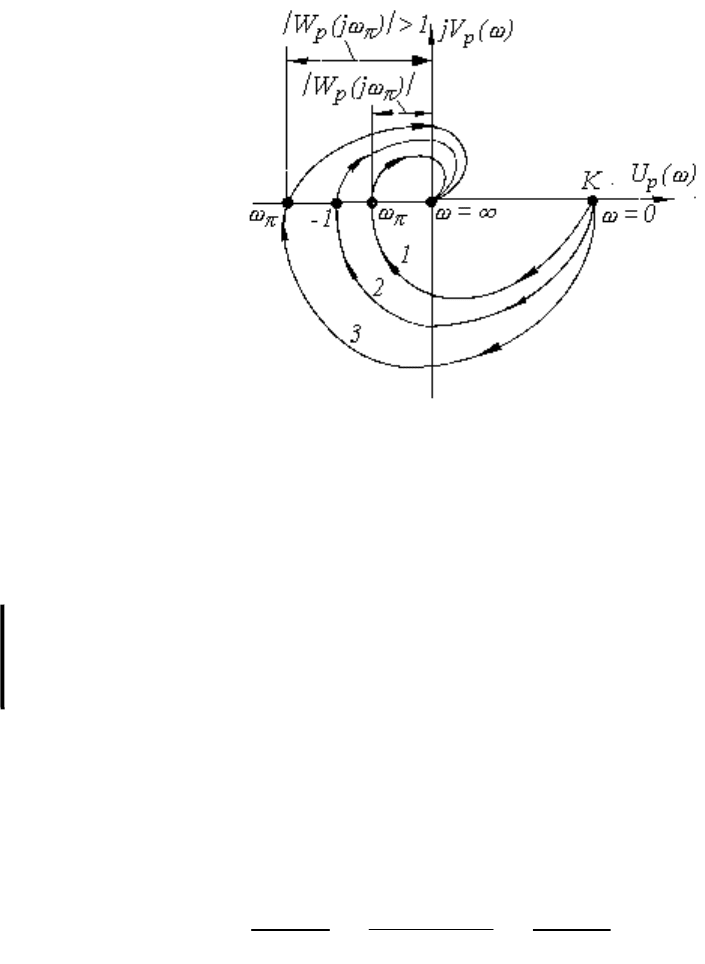
Отобразим три возможных варианта поведения замкнутой системы на плоскости АФХ
разомкнутой системы (см. рис. 4.3).
Рис. 4.3. Амплитудно-фазовые характеристики разомкнутой системы для трех вариантов
преобразования гармоники X
св
(j
) на частоте
Рассмотренная выше физическая трактовка динамических свойств замкнутой системы и
рис. 4.3 позволяют сделать заключение о том, что
если система устойчива в разомкнутом состоянии, то для устойчивости замкнутой
системы необходимо и достаточно, чтобы АФХ разомкнутой системы не охватывала
точку с координатами (1, j0).
Разомкнутая система неустойчива.
В этом случае наглядная физическая трактовка условий устойчивости практически
невозможна. Поэтому целесообразно воспользоваться принципом аргумента для
вспомогательной функции
(p) = 1 + W
p
(p) = 1 +
)(
)(
pD
pM
p
p
=
)(
)(
pD
pMD
p
pp
=
)(
)(
pD
pD
p
Ќ
, (4.17)
41

где D
p
(p) и D
з
(p) - характеристические многочлены соответственно замкнутой и разомкнутой
систем. При p=j
(j
) =
)j(
)j(
p
Ќ
D
D
и
arg
(j
) =
arg D
з
(j
) -
arg D
p
(j
). (4.18)
0
+
30
+
330
+
Если разомкнутая система неустойчива и характеристическое уравнение D
p
(p)=0 имеет m
корней с положительной действительной частью, то условие устойчивости системы в
замкнутом состоянии запишется на основании (4.15) и (4.18) в следующем виде:
arg
(j
) = n
/2 - (n - 2m)
/2 = 2
m /2. (4.19)
0
+
Это значит, что в этом случае условием устойчивости замкнутой системы является охват
годографом вектора
(j
) начала координат своей комплексной плоскости m /2 раз в
положительном направлении при изменении
от 0 до +
. Однако использовать такую
методику анализа устойчивости неудобно. Если же на основании (4.17) учесть, что
(p) = 1 + W
p
(p) или W
p
(p) =
(p)- 1. (4.20)
Это означает, что
(p) и W
p
(p) отличаются только постоянным смещением на единицу,
т.е. началу координат на плоскости
(p) соответствует на плоскости W
p
(p) точка с
координатами (-1, j0).
Вместо подсчета числа охватов АФХ разомкнутой системы точки с координатами (-1, j0)
целесообразно подсчитать разность между числом положительных (сверху вниз) и
отрицательных переходов (снизу вверх) отрезка (-1
-
) дей ствительной оси АФХ
разомкнутой системы (в частотном диапазоне от 0 до +
). Для устойчивости системы
в замкнутом состоянии эта разность должна быть равна m/2, где m - число корней
характеристического уравнения разомкнутой системы с положительной
действительной частью.
Примечание. Если АФХ разомкнутой системы начинается (при
=0) на отрезке (-1
-
)
действительной оси, то учитывается 1/2 перехода с соответствующим знаком.
Если разомкнутая система нейтрально устойчива, т.е. в состав W
p
(p) входят
интегрирующие звенья, то для анализа устойчивости замкнутой системы АФХ разомкнутой
системы должна быть дополнена окружностью бесконечно большого радиуса, проходящей в
отрицательном направлении число квадрантов, соответствующих числу интегрирующих
звеньев.
Пример 4.2. Передаточная функция разомкнутой системы
42

W
p
(p) =
)1(
)1(
2
2
1
pTp
pTk
.
Выполнить анализ устойчивости замкнутой системы с помощью критерия Найквиста для
двух случаев: T
1
<<T
2
и T
1
>>T
2
.
Характеристическое уравнение разомкнутой системы
p
2
(T
2
p + 1) = 0
имеет корни p
1,2
= 0 и p
3
= - 1/T
2
, т.е. эта система нейтрально устойчива и m=0.
АФХ разомкнутой системы показаны на рис. 4.4.
При T
1
<<T
2
АФХ разомкнутой системы пересекает один раз отрезок (-1
-
)
вещественной оси в отрицательном направлении, т.е. условие устойчивости замкнутой
системы не выполняется.
При T
1
>>T
2
разность между числом положительных и отрицательных переходов АФХ
разомкнутой системы отрезка вещественной оси (-1
-
) равна 1-1=0 и m=0, т.е. условие
устойчивости замкнутой системы выполнено.
Рис. 4.4. АФХ разомкнутой системы, рассматриваемой в примере 4.2. штрихпунктирной
линией обозначена основная часть АФХ W
p
(j
) для случая T
1
>>T
2
4.4. Анализ устойчивости по логарифмическим частотным характеристикам.
Запасы устойчивости
43
Анализ устойчивости по логарифмическим характеристикам ЛЧХ разомкнутых систем
выполняется на основе критерия устойчивости Найквиста-Михайлова.
АФХ разомкнутых систем в зависимости от пересечения с вещественной осью
относительно критической точки с координатами (-1, j0) можно подразделить на два типа:
первый, когда все точки пересечения АФХ с вещественной осью расположены справа от
критической точки (рис. 4.5); второй, когда точки пересечения АФХ с вещественной осью
расположены справа и слева от критической точки (рис. 4.4).
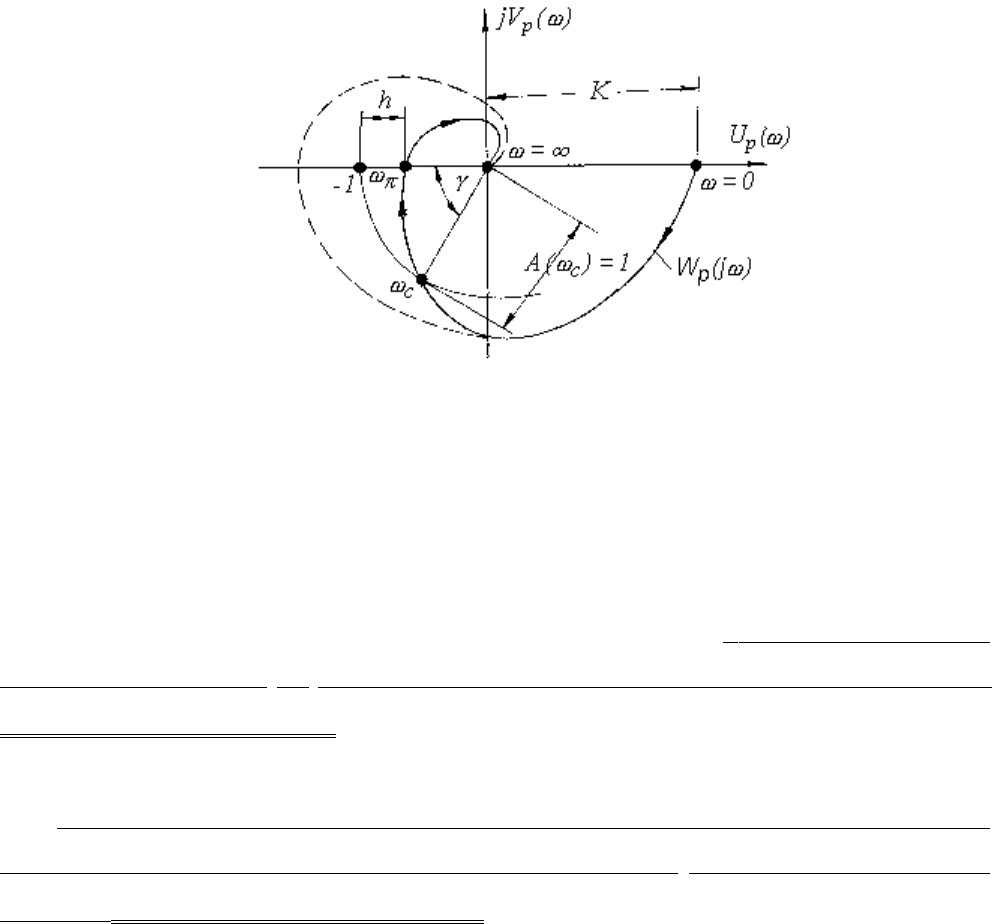
Рассмотрим взаимнооднозначное соответствие между АФХ первого типа и ЛЧХ.
Рис. 4.5. АФХ первого типа
АФХ первого типа, показанная на рис 4.5 сплошной линией, соответствует системе,
устойчивой в замкнутом состоянии. На этой АФХ выделены две частоты: частота среза (
с
),
при которой
W
p
(j
с
)
=А(
с
)=1 и частота
, при которой arg W
p
(j
)=
p
(
)=-180
.
Для устойчивых замкнутых систем удаление годографа W
p
(j
) от критической точки (-1,
j 0) характеризуется запасами устойчивости по фазе и модулю. Минимальный угол
,
образуемый вектором W
p
(j
с
) и отрицательной частью действительной оси, называется
запасом устойчивости по фазе
= 180
-
arg W
p
(j
с
)
(4.21)
Минимальный отрезок действительной оси h, характеризующий расстояние между
критической и ближайшей точкой пересечения годографом W
p
(j
) с действительной осью
называют запасом устойчивости по модулю.
Отобразим рис. 4.5 на плоскость ЛЧХ (рис. 4.6).
44
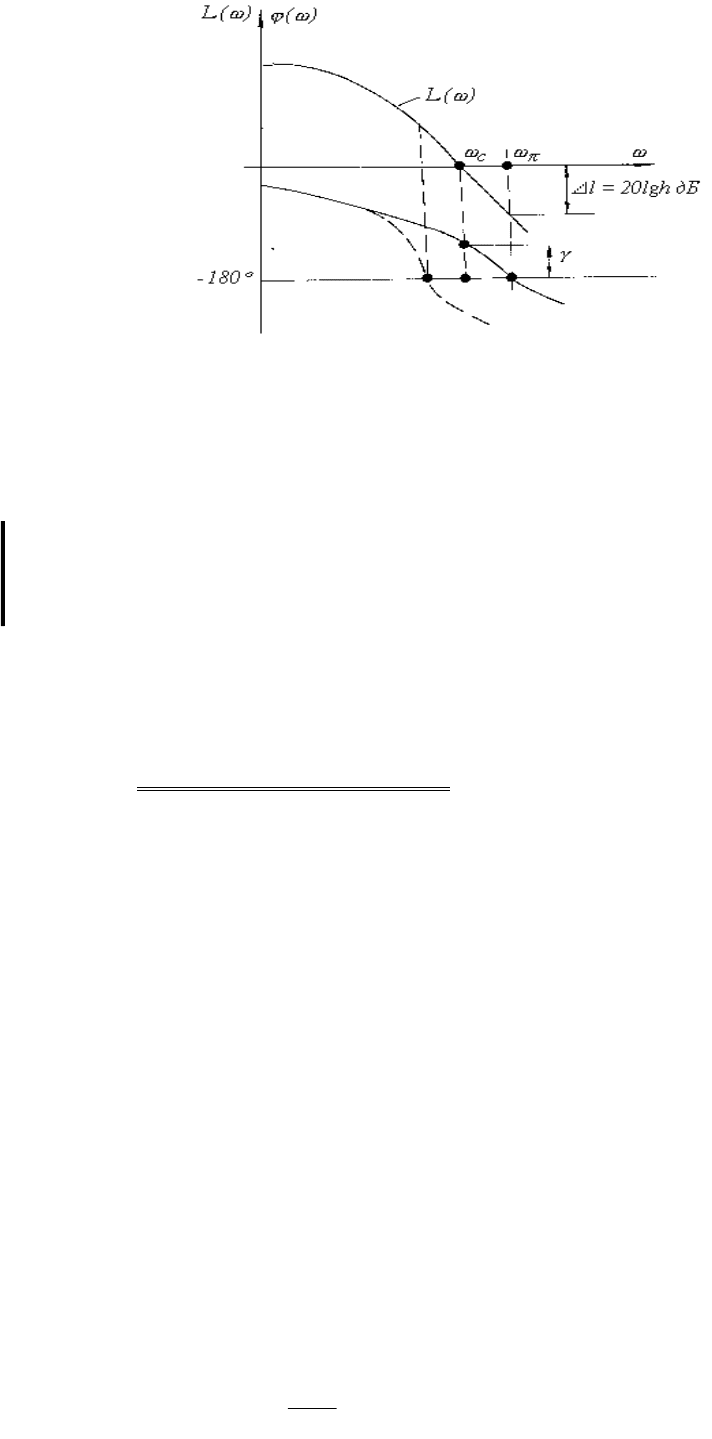
Рис. 4.6. Логарифмические частотные характеристики разомкнутой системы,
соответствующие устойчивой замкнутой системе (сплошные линии) и неустойчивой
замкнутой системе (пунктирная линия)
Рассмотренное позволяет сделать вывод:
система, устойчивая в разомкнутом состоянии и имеющая АФХ первого типа,
устойчива в замкнутом состоянии, если при всех частотах, при которых ЛАЧХ
положительна, т.е. L(
)
0,
(
)>-180
.
4.5. Влияние структуры и суммарного коэффициента системы на устойчивость
Существуют САУ, которые неустойчивы при любых значениях параметров. Такие
системы называют структурно неустойчивыми. Структурно неустойчивую систему можно
сделать устойчивой, изменив ее структуру.
Рассмотрим в качестве примера одноконтурную систему, содержащую одно
апериодическое звено и два интегрирующих звена. Характеристическое уравнение такой
системы имеет вид
(T
2
p + 1)
p
2
+ K = 0 (4.22)
и не содержит слагаемое с p в первой степени, т.е. a
1
=0. Очевидно, что в данном случае не
выполняется необходимое условие устойчивости - условие положительности коэффициентов
характеристического уравнения, и никакие вариации параметров T
2
и K не могут привести к
появлению слагаемого с p в первой степени. Следовательно, эта система структурно
неустойчива.
Существуют звенья, которые, как правило, ухудшают устойчивость системы, и звенья,
которые почти всегда улучшают устойчивость. К первой группе относятся звенья:
интегрирующее
W(p) =
pТ
1
и
; (4.23)
45

неустойчивое инерционное звено первого порядка
W(p) =
1pT
K
; (4.24)
консервативное
W(p) =
1
22
0
pT
K
. (4.25)
Звеньями, улучшающими устойчивость системы, являются форсирующие звенья. Обычно
используют форсирующие звенья первого порядка
W(p) = T
ф
p + 1. (4.26)
Рассмотрим общие условия структурной устойчивости одноконтурной системы.
Характеристическое уравнение замкнутой системы в общем случае имеет вид
D
з
(p) = D
p
(p) + M
p
(p) = 0,
где D
p
(p)=
)( pD
i
- произведение знаменателей передаточной функции отдельных
звеньев, входящих в контур системы;
M
p
(p) - произведение числителей этих же функций.
Условия структурной устойчивости зависят от порядка п характеристического уравнения
и вида многочленов D
p
(p) и M
p
(p). Обозначим:
- число интегрирующих звеньев (4.23);
t - число неустойчивых звеньев;
r - число консервативных звеньев, входящих в систему.
Если форсирующих звеньев в контуре нет, т.е. M
p
(p)=К (где - К коэффициент усиления
системы), то условие структурной устойчивости системы выражается в виде двух неравенств:
n.<4r
2;<t
(4.27)
Для более сложных видов многочлена M
p
(p) условия структурной устойчивости
одноконтурных систем приводятся в специальной литературе.
Рассмотрим влияние одного из основных параметров системы - суммарного
коэффициента усиления разомкнутого контура на ее устойчивость. Учтем, что для
одноконтурных систем коэффициент К входит в выражение ЧПФ W(j
) как множитель
W(j
) =
)j(D
)j(MK
p
*
p
, (4.28)
где
.1
0
)(
*
jM
p
46

Это означает, что длины вектора W(j
) при всех значениях
пропорциональны
коэффициенту К.
При увеличении коэффициента К АФХ расширяется (рис. 4.7,а) и приближается к
критической точке (-1, j0). Следовательно, увеличение добротности системы приводит к
нарушению устойчивости системы.
Это правило справедливо для большинства реальных систем, т.е. систем с АФХ первого
рода. Однако существуют системы с АФХ второго рода (рис. 4.7,б). В таких системах к
нарушению устойчивости может привести не только увеличение, но и уменьшение
коэффициента усиления.
Рис 4.7. Определение предельного значения коэффициента усиления
Значение коэффициента усиления, при котором АФХ разомкнутой системы проходит
через точку (-1, j 0), т.е. при котором замкнутая система находится на границе колебательной
устойчивости, называют предельным или критическим. Этот вопрос с помощью критерия
Гурвица рассматривался в 4.2 (см. пример 4.1).
Если A
p
(
) =
W
p
(j
)
= B (см. рис. 4.7,а), К
кр
= К/В.
Таким образом, установлена одна из важнейших в ТАУ закономерностей
чем больше суммарный коэффициент усиления разомкнутого контура регулирования,
тем ближе замкнутая система к границе устойчивости.
Предельное значение коэффициента усиления зависит от соотношения постоянных
времени звеньев, образующих контур системы. Рассмотрим систему, структурная схема
которой показана на рис. 4.8.
47

Рис. 4.8
Передаточная функция замкнутой системы
W
з
(j
) =
)p(F
)p(X
З
=
K)1pT)(1pT)(1pT(
K
321
n
, (4.29)
где K
= K
у
K
1
K
2
K
3
K
ос
D(p) = a
3
p
3
+ a
2
p
2
+ a
1
p + a
0
,
где
K1a
Т+ ТТ =a
ТТ + ТТ + ТТ =a
ТТТ =a
0
;
32
+
1 1
;
323121 2
;
321 3
(4.30)
Согласно критерию Гурвица система третьего порядка будет находиться на границе
колебательной устойчивости при
2
= а
1
а
2
- а
0
а
3
= 0. (4.31)
Подставив в уравнение (4.31) коэффициенты (4.30), получим
(Т
1
Т
2
+ Т
1
Т
3
+ Т
2
Т
3
)( Т
1
+ Т
2
+ Т
3
) - Т
1
Т
2
Т
3
(1 + К
КР
) = 0. (4.32)
Решив это равенство относительно К
КР
и выполнив некоторые дополнительные
преобразования (деление на а
3
), получим
К
КР
=
2
Т
Т
Т
Т
Т
Т
Т
Т
Т
Т
Т
Т
2
3
3
2
1
3
1
2
3
1
2
1
. (4.33)
На основании выражения (4.33) можно сформулировать важное практическое правило:
предельное значение добротности системы зависит от соотношения постоянных
времени и не зависит от их абсолютных значений.
В рассматриваемом случае К
КРмин
=8 при Т
1
=Т
2
=Т
3
.
Для увеличения К
КР
целесообразно уменьшать наименьшую постоянную времени.
Рассмотрим случай контура регулирования, состоящего из п одинаковых апериодических
звеньев с Т
i
=Т. Для нахождения К
КР
используем условия прохождения АФХ разомкнутого
контура через точку (-1;j 0). В этом случае частота среза
с
=
, что позволяет записать
следующие два уравнения:
48
