Грушинский Н.П. Основы гравиметрии

Подождите немного. Документ загружается.

Зная абсциссу Xi/„ при которой Дg достигает значения

Воспользовавшись формулой (9.17), легко получим

массу возмущающего тела

Если, кроме того, известна избыточная плотность тела, то,

предположив, что тело шарообразно, можно рассчитать ра

диус, а следовательно, и его объем:

1'е же рассуждения можно провести и для случая извест

ных градиентов

Кривая этой функции представлена на рис. 65. Она имеет

максимум при отрицательных х и минимум при положи

тельных. Над аномальным телом эта функция проходит

через нуль. Значения абсцисс, при которых функция до

стигает экстремумов, находим из условия

гтах, получаем

1 GM

(9.18)

откуда

h = l,31x1/2.

(9.19)

_ h- Agmax

(9 .20)

(9.21)

д(Угх) п

ZXi

дх

откуда

С.нимая с графика градиента Vzx абсциссы для хтлх и

vniill, найдем глубину залегания тела /г. Массу тела най

дем по формуле (9.14), которую напишем для максимальной

ординаты:

К2 3

(^)max = 3GM-

или

+ h2

s/2

M = l, 17^(V ZX)

0,858^ ?

(9.23)

Одной из уверенно решаемых гравиметрическим методом

мадач является задача определения глубины поверхности

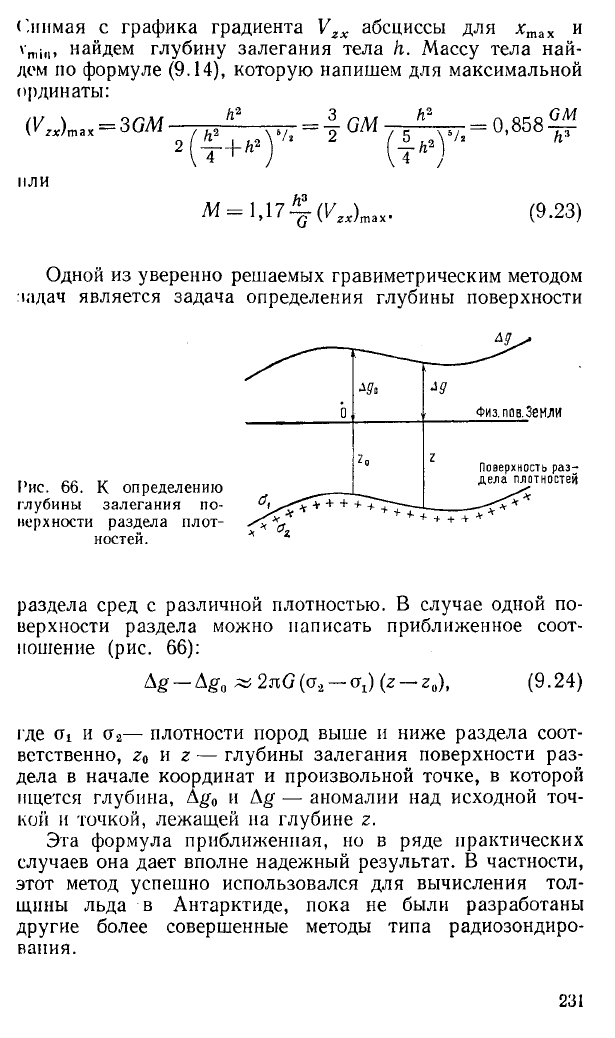
Рис. 66. К определению

глубины залегания по-

нерхности раздела плот

ностей.

раздела сред с различной плотностью. В случае одной по

верхности раздела можно написать приближенное соот

ношение (рис. 66):

Ag — Ag0 ^2nG{a.l — <тх) (z — 2 0), (9.24)

где (Ti и ст2— плотности пород выше и ниже раздела соот

ветственно, 20 и z — глубины залегания поверхности раз

дела в начале координат и произвольной точке, в которой

ищется глубина, Ago и Ag — аномалии над исходной точ

кой и точкой, лежащей на глубине г.

Эта формула приближенная, но в ряде практических

случаев она дает вполне надежный результат. В частности,

этот метод успешно использовался для вычисления тол

щины льда в Антарктиде, пока не были разработаны

другие более совершенные методы типа радиозондиро

вания.

§ 6. Понятие геолого-геофизического моделирования

и регуляризирующих алгоритмов

Как мы уже говорили, обратная задача неоднозначна и

трудно решаема. Практически удобным способом ее реше

ния является метод подбора: отыскание решения в специ

ально отобранном классе. Задача при этом становится

корректной, а получаемое решение — устойчивым.

В простейшем случае метод подбора состоит в том, что по

информации из других источников — геологическим дан

ным, сейсмическим и другим — строится предполагаемое

возмущающее тело. Ему придается некоторая простая

форма, предполагаются известными определенный избы

ток плотности и глубина залегания. Рассчитывается также

палетка, при помощи которой по конфигурации тела под

считывается его гравитационный эффект. Так строится

кривая первого приближения. Далее, по расхождениям

теоретических и наблюденных аномалий решают, как надо

подправить гипотетическую структуру. После ее исправле

ния вычисляют новые значения Ag и опять сравнивают с наб

люденной кривой. Так, последовательными приближениями

достигают хорошего совпадения расчетной кривой с наб

люденной.

Сейчас, когда в гравитационную разведку широко вошли

ЭВМ, этот способ усложнился и стал весьма эффективным.

Первым шагом в нем является построение геолого-геофизи-

ческой модели исследуемой области. Здесь используются

и полученные по сейсмическим данным границы горизонтов

с различными скоростями, и прослеживающийся геологи

чески характер напластований, и гипотетические аномаль

ные массы простейшей формы, например, в виде паралле

лепипедов. Задав все параметры такой модели, вычисляют

на ЭВМ плоское или пространственное аномальное гравита

ционное поле изучаемой области. Закрепляя один и варьи

руя другие параметры, осуществляют процесс итераций,

завершающийся построением геологической модели, хоро

шо согласующейся с гравитационной картиной. Этот спо

соб сейчас применяется все шире и шире и дает хороший

результат.

Другой подход к решению обратных задач заключается в

отыскании приближенного решения (квазирешения) с при

менением для этого регуляризирующих алгоритмов (по

А. Н. Тихонову). Проблема устойчивости решения воз

никает в связи с тем, что исходные данные получаются пу

тем измерений и определяются с некоторой погрешностью.

11('устойчивым называется такое решение (алгоритм), когда

малые изменения исходных данных ведут к очень большим

изменениям результата. Смысл регуляризации (получения

устойчивого квазирешения) заключается в том, что из фи

зических соображений находят некоторые характеристики,

которые могут ограничить искомые величины. Формализо

ванные (описанные математически) характеристики вклю

чаются в условие задачи. Решение этой новой задачи (ква-

шрешение) получается устойчивым, но «платой» за это

является потеря в точности.

Поясним это примером. Представим параметры pt, оп

ределяющие местоположение и размеры геологических

структур, компонентами некоторого вектора Р. Каждому

наблюденному значению рассматриваемой гравитационной

характеристики Vi набл (аномалии силы тяжести или ано

малии ее градиентов) поставим в соответствие ее теорети

ческий аналог Vt теор (Р). Искомый вектор параметров Р

находим из условия минимума среднеквадратической оста

точной погрешности:

иабл — V, .геор (Я), (9.25)

т. е. из условия минимума функционала

где D — оператор дисперсии.

В поисках устойчивого квазирешения функционал F

можно заменить сглаживающим:

Ma(P) = F(P) + ati(P), (9.26)

где регуляризирующий параметр а выбирается, как уже

говорилось, из физических соображений (например, на

кладывается ограничение на производную рассматриваемой

характеристики V). Регуляризатор Й(Р) можно выбрать

из следующих соображений. Потребуем, чтобы при мини

мизации искомые параметры не сильно отличались от сво

их начальных значений:

ГП

ЩР)= S Ь(Р;— рТ> (9.27)

/ = 1

qj— коэффициенты, играющие роль весовых функций.

Мели вариация параметра по геологическим данным долж

на быть небольшой, qj выбирается большим, если же геоло

гическая информация не ограничивает вариацию pj, то

соответствующий коэффициент выбирается малым или рав

ным нулю.

Г Л А В Л 10

МЕТОДЫ И ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЯ

УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ

§ 1. Принципы измерения ускорения силы тяжести

Способы измерения ускорения силы тяжести на Земле

основаны на физических явлениях, связанных с проявле

нием закона тяготения. Таковы свободное падение тел,

колебание свободного маятника или нагруженной струны,

равновесие пружинных или крутильных весов и др. Наз

ванные явления положены в основу нескольких классов

приборов для измерений ускорения силы тяжести: балли

стических гравиметров, маятниковых приборов, стати

ческих и струнных гравиметров. Все методы, а соответ

ственно и приборы разделяются на динамические и ста

тические. В первых ускорение силы тяжести получается

по измерениям частоты или периода колебания системы

или по измерениям пройденного пути и времени. Во вто

рых — по изменению положения равновесия чувствитель

ного элемента под действием приращения силы тяжести

g или по добавочной силе, приложенной для компенсации

этого изменения. Измерения могут быть абсолютными,

когда измеряется полная величина g, и относительными,

когда измеряется приращение силы тяжести к ее значению в

некотором исходном пункте. Рассмотрим основы определе

ния g из названных явлений.

Путь s, пройденный свободно падающим телом в поле сил

тяготения напряженности g, пропорционален квадрату

времени падения:

Отсюда

ё = (ЮЛ)

Измерив время t, за которое пройден известный путь s, по

лучим искомое значение ускорения силы тяжести. Однако

кажущееся простым решение сразу же осложняется, как

только определяется точность, с которой требуется изме

рить g. Соотношение точностей легко получить, если взять

логарифмическую производную левой и правой части урав

нения (10.1):

dg ^ ds__ 2 dt_ (10 2)

g s t У • /

I'.ели мы хотим определить g с относительной точностью

I • 10-8, что соответствует современным требованиям, то

с этой точностью надо измерить и путь s, пройденный телом,

и время (, а также обеспечить такое постоянство условий

эксперимента, чтобы возникающие погрешности не ухуд

шали требуемой точности. По этой причине метод свобод

ного падения тел, давно известный и даже использованный

в опытах Галилея, до последнего времени не имел практи

ческого значения.

Первым практическим методом измерения ускорения

силы тяжести был метод свободных колебаний маятника,

('вязь периода Т таких колебаний с

ускорением g свободного математи

ческого маятника обычно пишется в

виде бесконечного ряда:

T = 2 n Y j (! + 4 sin2T+

+ ^ s in ‘ £ + . . . ), (Ю.З.)

где i — длина нити подвеса, а — ам

плитуда (рис. 67).

Под математическим маятником

подразумевается идеальный маят

ник, состоящий из точечной массы,

подвешенной на идеально гибкой,

нерастяжимой и невесомой нити I

в абсолютном вакууме. Всякий маятник, состоящий из

протяженных масс и представляющий собой физическое

твердое тело, качающееся около некоторой горизонтальной

оси, называется физическим маятником. Такой маятник

совершает колебания по тому же закону, только роль длины

/ в формуле (10.3) выполняет в нем некоторая функция

формы, массы и расположения точки подвеса. Эта функцня

называется приведенной длиной маятника и имеет вид

Рис. 67. Схема опре"

деления g маятниксг

вым способом — мате"

матический маятник-

где / 0= 5 r2dm — момент инерции относительно оси кача

ли

ния маятника, а — расстояние от оси качания до центра

тяжести маятника, М — масса маятника.

Второй член ряда в формуле (10.3) равен 7* 10—7 при

практически применяемых амплитудах порядка 0°,5. Его

рассматривают как поправку за неизохронность вследствие

изменения величины амплитуды; остальные члены ряда пре

небрежимо малы. В этих допущениях формула, связываю

щая период колебания маятника с ускорением силы тяже

сти, принимает простой вид:

7 = 2я + j / j a 2, (10.4)

где второй член вводится как поправка за амплитуду, а коле

бания маятника могут рассматриваться как изохронные,

не зависящие от амплитуды.

Соотношение точностей, как и в случае свободного па

дения, получим с помощью логарифмической производной!

(Ю.5)

Это соотношение точно такое же, как и в случае свободного

падения, только отношение приращений пути к полному

пути заменяется на отношение приращения длины маят

ника к его полной длине, а значит, требования к точности

измерения длины и времени в маятниковом способе не от

личаются от таковых в способе свободного падения.

Однако это справедливо для измерения по одному коле

банию. В силу изохронности измерения можно произво

дить по большому числу колебаний. Тогда, при делении

длительности серии непрерывных колебаний на число коле

баний я, ошибка определения периода уменьшится в п раз.

Если вести наблюдения с маятником, имеющим период

Y секунды, и наблюдать 1 час, погрешность измерения

уменьшится в 7200 раз и требование к точности измерения

временного интервала снизится до 10-8-7200=7,2-10~5 с.

Длина маятника остается неизменной, конечно, при опре

деленных условиях, и измерить ее проще, чем измерить

путь падающего тела в пространстве. Это определило вы

бор метода.

Маятниковый метод был первым, который начали при

менять для точного измерения силы тяжести. Этому также

способствовала возможность производить с маятниками

относительные измерения, которые, как правило, бывают

точнее и легче осуществимы. При относительном методе

исключается необходимость измерения длины маятника,

считаемой постоянной. За этим постоянством надлежит

тщательно следить. И тогда остается измерение времени,

которое можно производить на четыре порядка грубее,

чем в методе свободного падения.

Принцип относительных измерений можно показать,

если написать формулы периода колебания маятника для

двух различных точек, в которых значения напряженно

сти поля соответственно ge и g при одинаковых условиях:

для исходной точки

Т. = 2 я / Г ,

для исследуемой точки

Т = 2п j /" — .

У g

Тогда, возводя в квадрат и деля одно на другое, получим вы

ражение для g через g0 и отношение квадратов периодов:

( 10.6)

Обычно искомое g представляют как функцию разностней

периодов колебания Т—Т0=АТ:

то /, . Д П -2

ё go(T0 + AT)* So^ + t J ‘

Раскладывая в ряд правую часть равенства, получим

8 « g o -2 g 0 Т 7 + 3£о ( i f ) 2- (10-7)

Последний член обычно мал и вводится как поправка.

Таким образом получаем формулу, связывающую при

ращение периода АТ при изменении силы тяжести Ag=

=g—go'-

A g 2Д Т

go~ Тв •

Если =980 ООО мГал, Г0= 0,508 с, A g= 1 мГал, то

1 —2Д Т

980 000 ~ Т„ '

откуда АТ= —2,6-10—7 с, т. е. при увеличении ускорения

силы тяжести на 1 мГал период качания маятника умень

шится на 2,6-10~7 с. Отброшенный член

(£ )’

при изменении силы тяжести на 1 мГал имеет

1 величину ~0,75-10 6 мГал.

В статических гравиметрах сила, действу-

ющая на массу m в гравитационном поле на

пряженности g, уравновешивается противо-

тд действующей силой упругости пружины или

закрученной нити, на которых подвешива-

Рис. 68. Схе- ется масса m

ма пружин- т, „

ных весов. Рассмотрим систему, в которой упругии

элемент совершает линейные перемещения

(рис. 68). Пусть длина пружины под нагрузкой mg в исход

ной точке, где g=go, равна /0. После перехода в другую

точку, где g—gi, пружина изменит свою длину, и она ста

нет равной li. Приращение длины /х—/0= А / при небольших

растяжениях, согласно закону Гука, пропорционально на

грузке

т Al = mAg, (10.8)

где т — коэффициент упругости, откуда

Ag = — Al = KAl.

6 от

В такой системе приращение силы тяжести пропорционально

растяжению и шкала такой системы линейна.

В гравиметрах вращательного типа груз на конце маят

ника, закрепленного на горизонтальной упругой нити в

положении, близком к горизонтальному, совершает вра

щательные движения. Момент силы тяжести в таком гра

виметре

Mg = mgl cos ос.

Этот момент уравновешивается моментом упругой силы

нити, на которой закреплен маятник:

mgl cos а = & (ft — а), (10.9)

где 0 — угол закручивания нити, а — угол наклона ма

ятника к горизонту, k — крутильная жесткость нити. По

скольку в уравнение равновесия входит косинус угла за

кручивания, зависимость этого угла от изменения силы тя

жести оказывается нелинейной.

2. Фрагменты истории развития методов

и инструментов для гравиметрических измерений

Закон ускорения свободного падения был впервые сфор

мулирован Г. Галилеем (1564— 1642) около 1590 г. Он же

произвел первые опыты и получил значение g. Однако его

опыты были весьма грубы.

В 1784 г. английский физик Д. Атвуд изобрел приспо

собление, искусственно уменьшающее ускорение падения

тел и тем самым снижающее требование к точности измере

ния интервала времени. С помощью этого инструмента он

измерил величину g.

Первое измерение абсолютного значения ускорения си

лы тяжести с помощью машины Атвуда в России осуще

ствил в 1892 г. профессор Киевского университета

1'. Г. Метц (1861— 1930). Он получил значение £=981,24 Гал,

довольно близкое к истинному.

Однако метод падения для измерения абсолютного зна

чения g в то время был мало перспективен. Тогда еще не

умели точно измерять малые отрезки длины и времени, и

внимание исследователей было направлено на маятники.

11оследним экспериментом такого рода была работа петер

бургского ученого А. А. Иванова, который построил по

предложению Д. И. Менделеева прибор типа машины

Атвуда большого размера. Он получил в 1903—1904 гг.

значение £=981,48, однако пришел к выводу, что метод не в

состоянии конкурировать с маятниковым.

Одно из первых измерений силы тяжести маятником было

произведено Ш. Лакондамином (1701—1774) в 1735 г. в Сан

Доминго на острове Гаити во время экспедиции, проводив

шей измерение длины дуги меридиана в 1° вблизи экватора.

Он измерил длину секундного маятника L, которая свя

зана со значением g простым соотношением g^4 n 2L, кото

рое получается из (10.4) при Т= \ с. Лакондамин получил

значение L =990,85 мм и g= 977,9 Гал. Эти измерения де

лались в основном для установления меры длины. Лакон

дамин предложил за единицу длины принять длину секунд

ного маятника под экватором. С этой же целью Д. Борда

(1739—1799) и Я. Кассини (1748— 1845) в 1792 г. в Париже

вновь произвели измерение длины секундного маятника и

получили £=980,867 Гал, что соответствует L = 993,827 мм.

В 1808—1818 гг. французский физик Ж- Био (1774— 1862)

повторил их опыт с усовершенствованным инструментом.

В 1825—1826 гг. в Кенигсберге произвел свои измере

ния силы тяжести нитяным маятником знаменитый Ф. Бес