Грушинский Н.П. Основы гравиметрии

Подождите немного. Документ загружается.

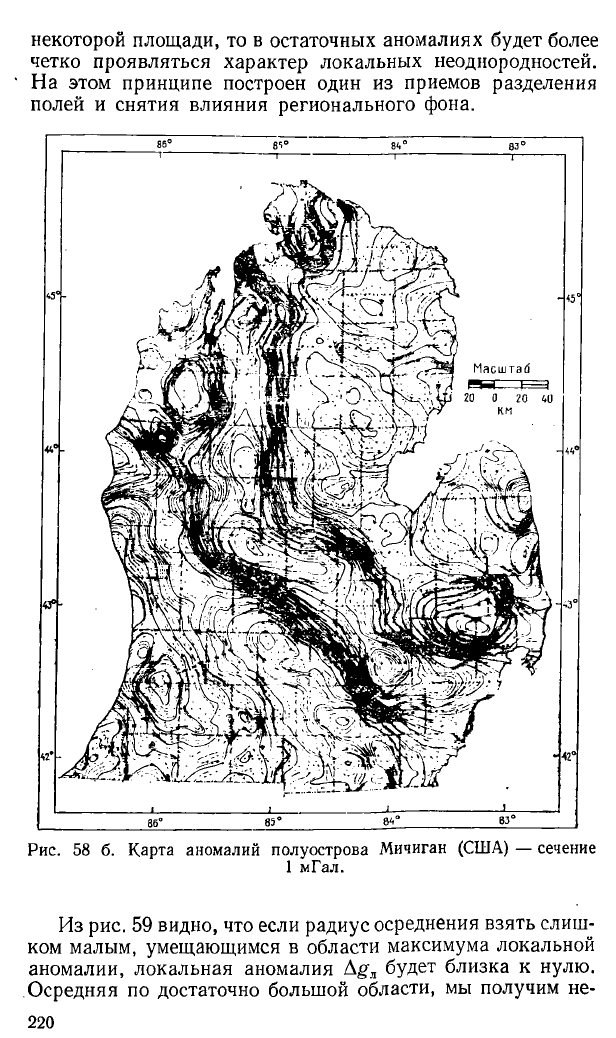
некоторой площади, то в остаточных аномалиях будет более

четко проявляться характер локальных неоднородностей.

На этом принципе построен один из приемов разделения

полей и снятия влияния регионального фона.

Рис. 58 б. Карта аномалий полуострова Мичиган (США) — сечение

1 мГал.

Из рис. 59 видно, что если радиус осреднения взять слиш

ком малым, умещающимся в области максимума локальной

аномалии, локальная аномалия Agx будет близка к нулю.

Осредняя по достаточно большой области, мы получим не

которую среднюю, близкую к региональной, аномалию.

Тогда

А ё л = а£изм - Д £ Р « А ^ и з м - A g cp = А ^ л »

где А^л — приближенное, оценочное значение локальной

аномалии, AgB3M — измеренное значение аномалии.

Рис. 59. Снятие регио

нального фона Agp мето

дом осреднения.

\л9р 1д?ср г

Одной из разновидностей снятия регионального поля

является метод осредненных градиентов, предложенный

С. Саксовым и К. Нигардом. Он состоит в том, что строится

функция

• <9 -з >

причем Ag-Cp (гг) и Ag-Cp (г2) — аномалии, осредненные по ок

ружностям радиуса гх и г2,— находят по формуле

2я

A f f c p W

= - 4

g(rh Q)dQ.

(9.4)

Практически Agcp (г,) получается как среднее из восьми

значений Agj, полученных с карты аномалий для точек,

равномерно расположенных на окружности радиуса г,-:

A g cp(/-f) = - g - 2 A gy. (9.5)

/ = i

Выбор радиусов окружностей осреднения зависит от формы

и глубины залегания тела, возбуждающего локальный гра

витационный эффект. Существенно выбрать внешний радиус.

Внутренний радиус выгодно иметь близким к первому,

если надежно известна глубина залегания. Полосу г2—гх

следует расширять при неточном знании глубины. Покажем

сказанное на примере.

Рассмотрим плоскую задачу для шарообразной возму

щающей массы (рис. 60). Наибольший горизонтальный

градиент гравитационного эффекта такой массы, очевидно,

имеет место в точках а, а'. Функция F (см. (9.3)) в пределе

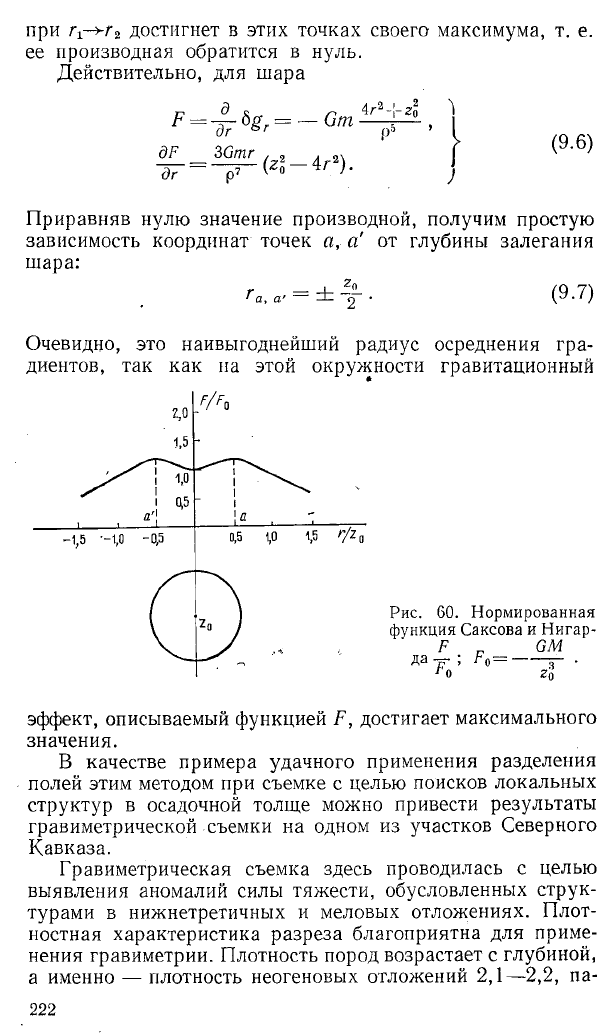
при гх->гг достигнет в этих точках своего максимума, т. е.

ее производная обратится в нуль.

Действительно, для шара

F -

_Э

дг

3Gmr

дг

Р7

в * ,=

(2о — 4г2).

(9.6)

Приравняв нулю значение производной, получим простую

зависимость координат точек а, а' от глубины залегания

шара:

га.а> = ± (9.7)

Очевидно, это наивыгоднейший радиус осреднения гра

диентов, так как на этой окружности гравитационный

Рис. 60. Нормированная

функция Саксова и Нигар-

F _ GM

да -jr ; Fо =

------

1 о г'0

эффект, описываемый функцией F, достигает максимального

значения.

В качестве примера удачного применения разделения

полей этим методом при съемке с целью поисков локальных

структур в осадочной толще можно привести результаты

гравиметрической съемки на одном из участков Северного

Кавказа.

Гравиметрическая съемка здесь проводилась с целью

выявления аномалий силы тяжести, обусловленных струк

турами в нижнетретичных и меловых отложениях. Плот-

ностная характеристика разреза благоприятна для приме

нения гравиметрии. Плотность пород возрастает с глубиной,

а именно — плотность неогеновых отложений 2,1—2,2, па-

леогеновых 2,3—2,4, меловых 2,4—2,6 и, наконец, палеозоя

2,75—2,8 г/см3. Согласно произведенным подсчетам гра-.

витационныи эффект, создаваемый локальными структу

рами, равен-0,8:— 1,3 мГал. Для более успешного решения

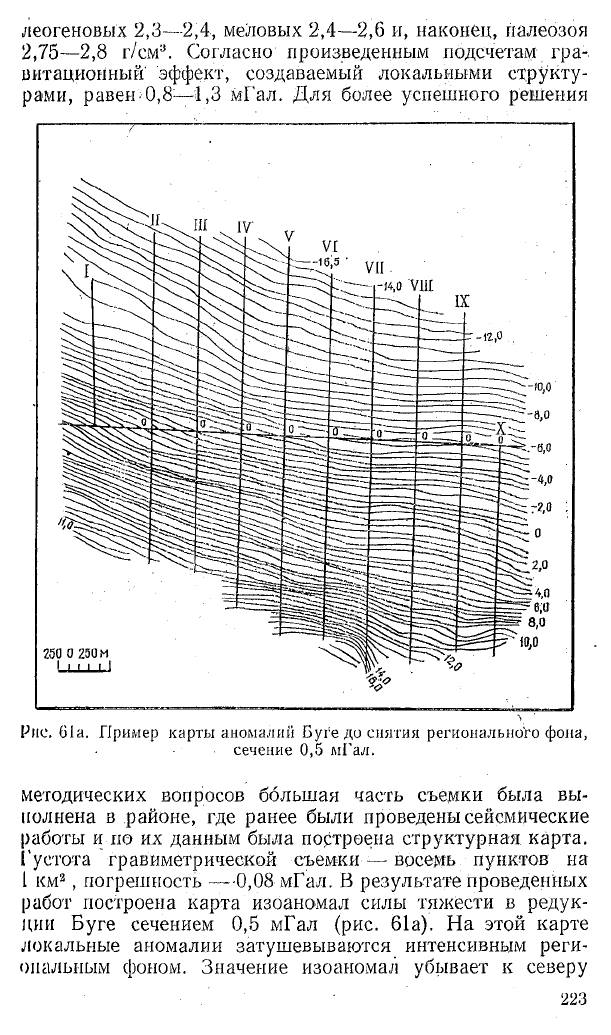
Рис. 61а. Пример карты аномалий Буге до снятия регионального фона,

сечение 0,5 мГал.

методических вопросов большая часть съемки была вы

полнена в районе, где ранее были проведены сейсмические

работы и по их данным была построена структурная карта.

Густота гравиметрической съемки — восемь пунктов на

I км2, погрешность — -0,08 мГал. В результате проведенных

работ построена карта изоаномал силы тяжести в редук

ции Буге сечением 0,5 мГал (рис. 61а). На этой карте

локальные аномалии затушевываются интенсивным реги

ональным фоном. Значение изоаномал убывает к северу

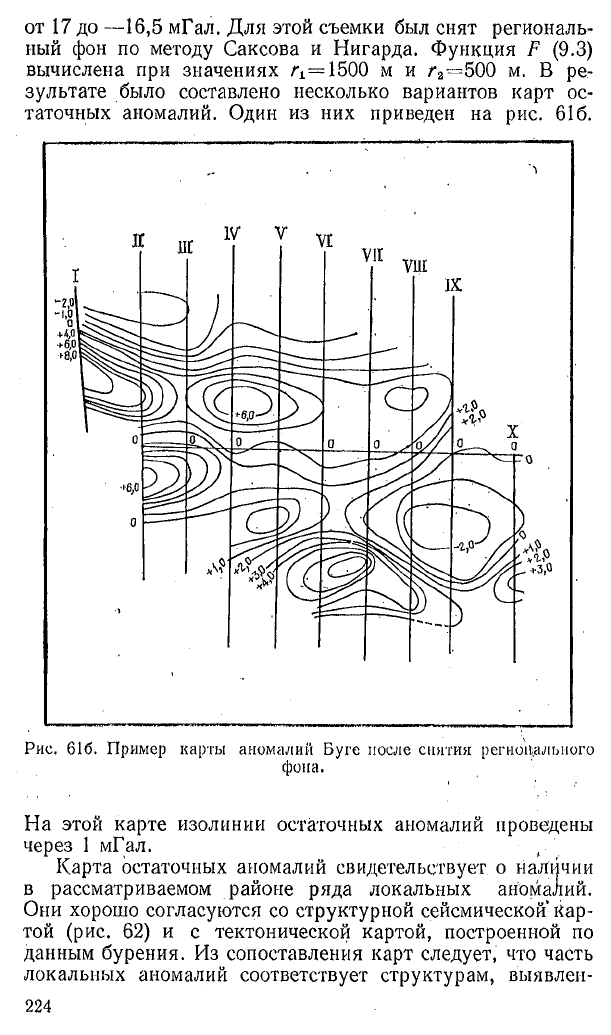
от 17 до —16,5 мГал. Для этой съемки был снят региональ

ный фон по методу Саксова и Нигарда. Функция F (9.3)

вычислена при значениях /-!= 1500 м и /v=500 м. В ре

зультате было составлено несколько вариантов карт ос

таточных аномалий. Один из них приведен на рис. 616.

На этой карте изолинии остаточных аномалий проведены

через 1 мГал.

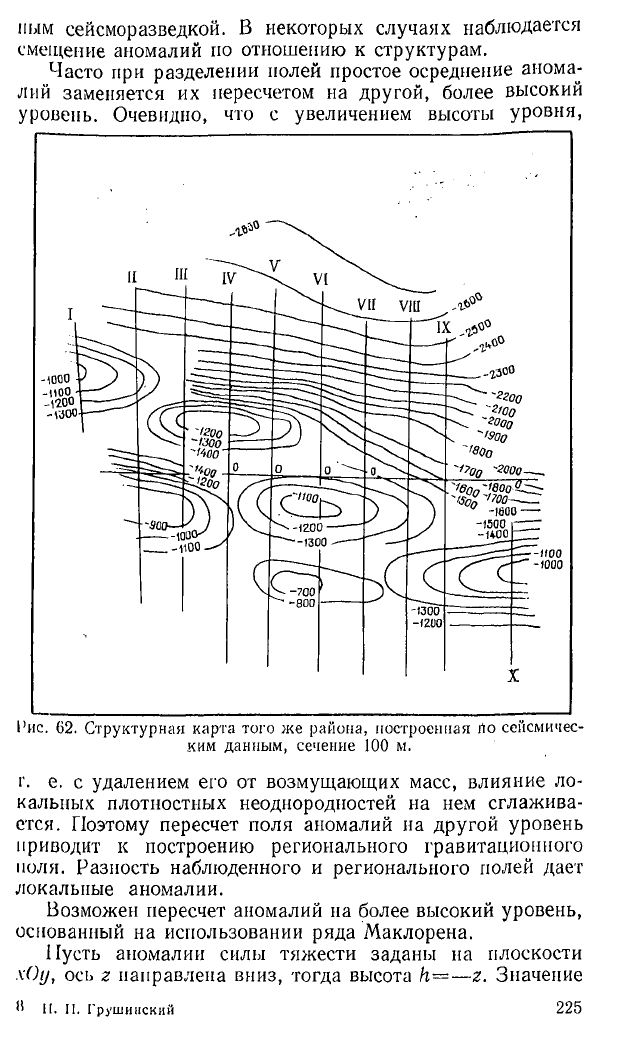
Карта остаточных аномалий свидетельствует о наличии

в рассматриваемом районе ряда локальных аномалий.

Они хорошо согласуются со структурной сейсмической'Кар

той (рис. 62) и с тектонической картой, построенной по

данным бурения. Из сопоставления карт следует, что часть

локальных аномалий соответствует структурам, выявлен-

мим сейсморазведкой. В некоторых случаях наблюдается

смещение аномалий по отношению к структурам.

Часто при разделении полей простое осреднение анома

лий заменяется их пересчетом на другой, более высокий

уровень. Очевидно, что с увеличением высоты уровня,

1’ис. 62. Структурная карта того же района, построенная rto сейсмичес

ким данным, сечение 100 м.

г. е. с удалением его от возмущающих масс, влияние ло

кальных плотностных неоднородностей на нем сглажива

ется. Поэтому пересчет поля аномалий на другой уровень

приводит к построению регионального гравитационного

поля. Разность наблюденного и регионального полей дает

локальные аномалии.

Возможен пересчет аномалий на более высокий уровень,

основанный на использовании ряда Маклорена.

Пусть аномалии силы тяжести заданы на плоскости

х()у, ось z направлена вниз, тогда высота h——z. Значение

силы тяжести в точке с высотой h может быть выражено по

известной аномалии в точке с /г=0 рядом Маклорена:

Ag(x, у, -h ) = Ag(x, у, 0) — h (д- {хдгу’ г))г = 0 +

, Л2 (d2Ag(х, у, г)\ , /n Q,

+ -т {— ш*— ;*=„+■■• (9-8)

Первые и вторые производные аномалии суть аномальный

вертикальный градиент и изменение аномального верти

кального градиента силы тяжести. Они могут быть полу

чены расчетным путем на основе аномалии в точке х, у, 0.

Вертикальный градиент можно также измерить.

Возможен пересчет на более высокий уровень с помощью

интеграла Пуассона. Интеграл Пуассона определяет гар

моническую функцию в любой точке внешнего полупро

странства, ограниченного сферой или плоскостью, при

условии, что функция задана на этой сфере или плоскости

(внешняя задача Дирихле).

Рис. 63. К пересчету аномалий на высоту с помощью интеграла Пуас

сона.

Для точек внешнего полупространства интеграл Пуас

сона имеет вид

(9.9)

где Ag(M) — аномалия силы тяжести в точке М, располо

женной на высоте Я над бесконечной плоскостью S, Ag(P) —

аномалия силы тяжести в текущей точке Р на плоскости S,

р — расстояние между точками М и Р (рис. 63). Вводя

полярные координаты с началом в точке О, формулу (9.9)

можно представить в виде

A g (M )« j

' h Agcp (r)rd/-

(/i2 + r2)s/l

1 Де Ag'cp (r) — средняя аномалия по окружности радиуса г:

2xt

Agcp(/- )= \ Аё ( г> ф )^ ; (9Л1)

Ф —- угол в плоскости х, у, отсчитываемый от направ

ления нулевого меридиана.

Для практического применения формула (9.10) приб

лиженно представляется суммой интегралов:

А / д iv л&(0) -г Agcp (Л) f hr dr

A g(M) =

-----------

s— i— 1

(h2-*- r2)’^‘

Agcp (h) — Agcp (k) f hr dr

2) i n r u r

ГЛ -r*)*

(9.12)

где li, /2, • • •— радиусы окружностей, которыми делится

плоскость на кольцевые зоны, Ag'cp(/1), Д^ср(/2), . . . —

средние аномалии силы тяжести на окружностях с радиу

сами /ь 12, . . Ag(0) — значение аномалии силы тяжести

п начале координат.

Выполняя интегрирование, получим рабочую формулу

для пересчета аномалий на более высокий уровень:

Ag(M) =

Agcp (0)

, Agcp (/2)

(л2+ /!)‘Ч

Agcp (h)

(/12 + /?)‘Л (л2-НЮ‘/г

(ЛЧ

+ . .. (9.13)

Обычно берут /! = -£-/г, /2=^/г, l3=2h и т. д. После того как

выделены локальные аномалии, возникает задача их интер

претации.

§ 4. Прямая задача гравитационной разведки

Прямая задача гравитационной разведки состоит в по

строении теоретическим путем гравитационного поля ло

кальных аномалий Ag или вторых производных возмущаю-

8 * 227

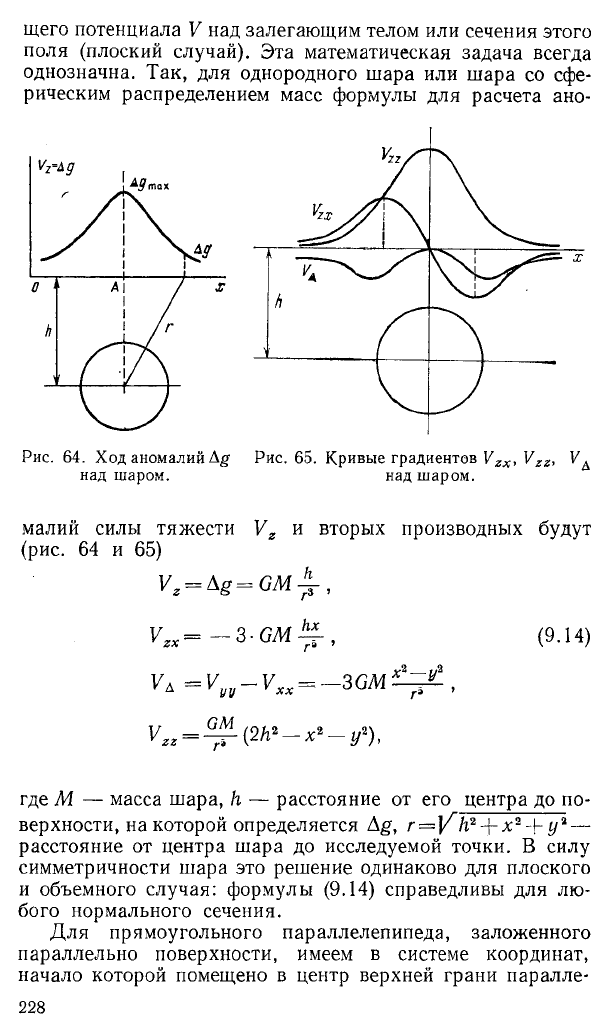
щего потенциала V над залегающим телом или сечения этого

поля (плоский случай). Эта математическая задача всегда

однозначна. Так, для однородного шара или шара со сфе

рическим распределением масс формулы для расчета ано-

Рис. 64. Ход аномалий Ag Рис. 65. Кривые градиентов Vzx, Vzz,

над шаром. над шаром.

малий силы тяжести Vг и вторых производных будут

(рис. 64 и 65)

Уг = А g = G M ± ,

Vzx= — 3 • GM , (9.14)

V ь. = V yv — Vxx= 3 GM г

Vzz= ™ (2 h*-x*-y*),

где M — масса шара, h — расстояние от его центра до по

верхности, на которой определяется Ag, r= V h2 + %2 + у% —

расстояние от центра шара до исследуемой точки. В силу

симметричности шара это решение одинаково для плоского

и объемного случая: формулы (9.14) справедливы для лю

бого нормального сечения.

Для прямоугольного параллелепипеда, заложенного

параллельно поверхности, имеем в системе координат,

начало которой помещено в центр верхней грани паралле-

hg — 2Go a ln ^ p l

Vzx = Go In

У a2 + &24~z2— b z2

V a.2 + b2 4- г2 + b _ Zl ’

VZy=Ga In

_________________ ,

У с Р + Ь * + г * — а 2

/' а 2 + 62 + г2 + а Jz, J

■Чдесь йи!) — половина длины параллелепипеда по осям х

и у, г — длина диагонали параллелепипеда.

Решены прямые задачи для тел различных конфигу

раций: для вертикального и горизонтального круговых ци

линдров, для полусферы, шарового сегмента, кругового

полуцилиндра, уступа, эллипсоидального цилиндра и т. п.

Существуют альбомы, показывающие ход кривых Ag и

вторых производных потенциала притяжения Vгх, Vг ,

Ухх, Ууу, Vzz, Vху над этими телами. Потенциал и его про

изводные для тел сложной формы могут быть найдены

суммированием эффектов от простых тел.

§ 5. Обратная задача гравитационной разведки

Обратная задача гравитационной разведки состоит в

определении параметров возмущающего тела по характеру

возбужденного им гравитационного поля. Это именно та

задача, которую и призван решать метод гравитационной

разведки. В результате наблюдений получено гравитаци

онное поле: кривая Ag вдоль профиля наблюдений (пло

ский случай) или построена гравиметрическая карта обла

сти, в которой предполагается наличие искомых геологиче

ских структур. Требуется по этим данным определить массу

тела, его форму, глубину залегания. В общем виде эта за

дача некорректна *), а во многих случаях и не решаема.

Чаще всего удается решить какую-то часть ее, например

определить глубину залегания центра масс.

Пример такого решения для определения глубины зале

гания центра масс уже рассмотрен в главе 5. Теперь опре

делим массу тела.

В точке А над центром масс (рис. 64) притяжение дости

гает максимума. При этом радиус-вектор точки A r=h, так

* ) З а д а ч а

называется корректно поставленной, если ее решение

существует, если оно единственно и устойчиво.