Hassani S. Mathematical Methods: For Students of Physics and Related Fields

Подождите немного. Документ загружается.

254 Vectors in Relativity

Example 8.4.4. Let a constant force act on a particle of mass m in some inertial

frame. What is the speed of the particle at time t if it starts from rest?

Equation (8.44) can be trivially integrated to give p =



Ft. Since the force is

constant, the motion takes place in one dimension. So, we can ignore the vector

sign and (remembering that β = v/c)write

mγv = Ft, or mγβ =

, or



1 − β

Squaring both sides and solving for β gives

β =

Ft/mc



1+(Ft/mc)

, or v =

Ft/m



1+(Ft/mc)

. (8.47)

Note that for large t (i.e., when Ft >> mc), β ≈ 1orv ≈ c. However, the particle

can never attain the speed of light no matter how long we wait. On the other hand,

if Ft << mc,thenv =(F/m)t, which is the Newtonian speed of a particle moving

with constant acceleration.

It is interesting to consider a particle having a constant acceleration of 10 m/s

(approximately Earth’s gravitational acceleration). How long does it take to attain a

speed of 0.999c? Over 21 years! (See Problem 8.14). On the other hand, Newtonian

mechanics requires under one year to achieve the same speed!



8.5 Problems

8.1. Show that Equation (8.6) follows from Equation (8.5). Hint: Consider

the three vectors a, b,andc = a + c.

8.2. Multiply the matrices in Equation (8.10) to obtain the three equations

of (8.11). Solve these equations to ﬁnd all matrix elements in terms of a

8.3. In Example 8.3.1, Emmy receives the two signals from the explosions at

the same time.

(a) Show that this time is L/(2c) according to Emmy, and γL/(2c) according

to Karl.

(b) Let T



and T



denote the times that Karl receives the signal from the

front and back ﬁrecrackers, respectively. Show that



1+β

1 − β



1 − β

1+β



≡ T



−T



related to Δt



calculated in Example 8.3.1? Discuss

your answer.

8.4. Show that the relativistic law of addition of velocities (8.17) prohibits

the sum of two large velocities to be larger than the speed of light. Hint:

Multiply both sides of β

< 1by1− β.

8.5. Show that the 4-acceleration is η-orthogonal to the 4-velocity.

8.5 Problems 255

8.6. Provide the details of the proof of the statement: a particle is massless

if and only if it moves at light speed.

8.7. Apply (8.31) to a photon moving in the x-direction and use |p| = E/c

to show that



1 − β

1+β

Now use E = hc/λ to ﬁnd a formula for the relativistic Doppler shift.

8.8. Two identical particles of mass m approach each other along a straight

line with speed v = βc as measured in the lab frame. Show that the energy

of one particle as measured in the rest frame of the other is

1+β

1 − β

8.9. A particle of mass m and relativistic energy 4mc

collides with another

stationary particle of mass 2m and sticks to it. What is the mass of the

resulting composite particle.

8.10. An electron of kinetic energy 1 GeV (10

eV) strikes a positron (anti-

electron) at rest and the two particles annihilate each other and produce two

photons, one moving in the forward direction (the direction that electron had

before collision) and the other in the backward direction. What are the ener-

gies of the two photons. The mass (times c

) of electron and positron are the

same and equal to 0.511 MeV (10

eV).

8.11. A particle of mass m and energy E collides with an identical particle

at rest. The collision results in the formation of a single particle. Show that

the mass and the speed of the formed particle are, respectively,



2m(E + m)

and



(E − m)/(E + m), assuming that c =1.

8.12. A photon of energy E is absorbed by a stationary nucleus of mass m.

The collision results in an excitation of the nucleus. Show that the mass and

the speed of the excited nucleus are, respectively,



m(2E + m)andE/(E +

m), assuming that c =1.

8.13. Use Equations (8.21), (8.43), (8.45), and the orthogonality of the 4-

velocity and 4-acceleration to show that f

= γ



β ·



F .

8.14. How long does it take a particle to attain a speed of 0.999c,ifits

acceleration is 10 m/s

? What is the answer based on Newtonian mechanics?

How do the answers change if the ultimate speed of the particle is 0.99999c?

Part III

Inﬁnite Series

Chapter 9

Inﬁnite Series

Physics is an exact science of approximation. Although this statement sounds

like an oximoron, it does summarize the natureofphysics. Allthelawswedeal

with in physics are mathematical laws, and as such, they are exact. However,

once we try to apply them to Nature, they become only approximations.

Therefore, methods of approximation play a central role in physics. One such

method is inﬁnite series which we study in this chapter.

9.1 Inﬁnite Sequences

An inﬁnite sequence is an association between the set of natural numbers inﬁnite sequence

(often zero is also included) and the real numbers, so that for every natural

number k there is a real number s

. Instead of the association, one calls the

collection of real numbers the inﬁnite sequence. Two common notations for

a sequence are an indicated list, and enclosure in a pair of braces, as given

below:

,...,s

,...}≡{s

}

∞

k=1

Instead of k, one can use any other symbol usually used for natural numbers

such as i, j, n, m,etc. Wecalls

the nth term of the sequence.

In practice, elements of a sequence are given by a rule or formula. The

following are examples of sequences:

(

,...

)

(

)

∞

n=1









,...



k +1



∞

k=1

(

,...

)

(

)

∞

j=1

(

, −

,...

)

(

(−1)

m+1

m +1

)

∞

m=1

(9.1)

An important sequence is the sequence of partial sums in which each

term is a sum. Examples of such sequences are the following:

sequence of partial

sums

260 Inﬁnite Series

(

1, 1+

, 1+

, ...

)

(

1, 1+

, 1+

, ...

)

(

1, 1+

, 1+

, ...

)

(

1, 1+1, 1+1+

, ...

)

The nth term of the sequences above are, respectively,

=1+

+ ···+



k=0

=1+

+ ···+



i=1

=1+

+ ···+



j=1

=1+1+

+ ···+



k=0

so that the sequences can be written, respectively, as

convention:

0! = 1.



k=0

∞

n=0



i=1

∞

n=1

⎧

⎨

⎩



j=1

⎫

⎬

⎭

∞

n=1



k=0

∞

n=0

. (9.2)

In the last sequence, we have used the usual deﬁnition, 0! ≡ 1. A sequence is

convergence and

limit of a sequence

said to converge to the number s or to have limit s if for every positive (usu-

ally very small) real number  there exists a (usually large) natural number

N such that |s

− s| <whenever n>N.Wethenwrite

lim

n→∞

= lim

ν→∞

= lim

♣→∞

♣

= lim

♥→∞

♥

= s. (9.3)

Note the freedom of choice in using the symbol of the limit. A sequence that

does not converge is said to diverge. The ﬁrst three sequences in Equation

(9.1) are convergent and their limits are

lim

n→∞





=0, lim

n→∞



n +1



= e, lim

n→∞





=0.

The last sequence diverges because there is no single number to which the

terms get closer and closer.

There are many ways that a sequence can converge to its limit. For in-

stance, the terms s

may steadily increase toward s after some large integer

9.1 Inﬁnite Sequences 261

(a)

(b)

(c)

(d)

(e)

(f)

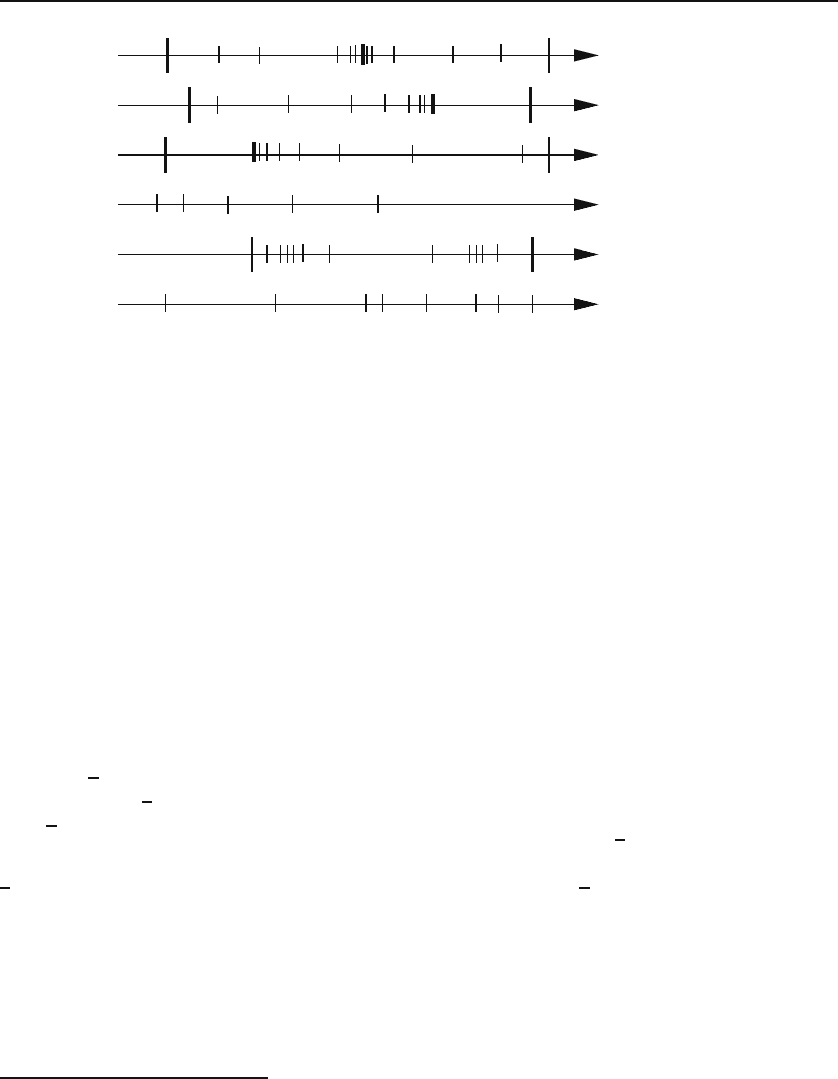
Figure 9.1: Types of sequences and modes of their convergence: (a) convergent, (b)

convergent monotone increasing, (c) convergent monotone decreasing, (d) divergent

monotone increasing, (e) divergent bounded, (f) divergent unbounded.

N, so that for all n ≥ N, s

≤ s

n+1

≤ s

n+2

≤ s

n+3

≤···.

In this case

we say that the sequence is monotone increasing.Ifthetermss

steadily monotone

increasing,

monotone

decreasing, and

bounded

sequences

decrease toward s after some large integer N, the sequence is called mono-

tone decreasing. A sequence may bounce back and forth on either side of

its limit, getting closer and closer to it. A sequence is called bounded if there

exist two numbers A and B such that

A ≤ s

≤ B for all n.

A sequence may be bounded but divergent. Various forms of convergence and

divergence are depictedinFigure9.1.

A sequence may have an upper and/or a lower limit. The upper limit is

anumbers such that there are inﬁnitely many n’s with the property that s

is very close to s if n is large enough, and there is no other number larger

than

s with the same property. Similarly, the lower limit is a number s such

that there are inﬁnitely many n’s with the property that s

is very close to

if n is large enough, and there is no other number smaller than s with the

same property. The last sequence of Equation (9.1) has an upper limit of 1

and a lower limit of −1. It is intuitively obvious that a sequence converges if

and only if its upper and lower limits are ﬁnite and equal. For instance, the

sequence {(−1)

/n}

∞

n=1

converges to the single limit 0 after bouncing left and

right of it inﬁnitely many times.

One can decide whether a sequence converges or not without knowing its

limit:

Cauchy criterion

We often use the loose phrase: “For large enough n, . . . .” The precise statement would

be: There exists an N such that for all n ≥ N,....

262 Inﬁnite Series

Box 9.1.1. (Cauchy Criterion). The sequence { s

}

∞

n=1

converges if

the diﬀerence s

−s

approaches zero as both m and n approach inﬁnity.

We can add, subtract, multiply, and divide two convergent sequences term

by term and obtain a new sequence. The limit of the new sequence is obtained

by the corresponding operation of the limits. Thus, if

lim

n→∞

= x, lim

n→∞

= y,

then

lim

n→∞

± y

)=x ± y, lim

n→∞

· y

)=x · y, lim

n→∞

provided, of course, that y = 0 when it is in the denominator.

9.2 Summations

We have been using summation signs on a number of occasions, and we shall

be making heavy use of them in this chapter as well. It is appropriate at

this point to study some of the properties associated with such sums. Every

summation has a dummy index which has a lower limit, usually written

dummy

summation index

can be any symbol

you want it to be!

under the summation symbol



,andanupper limit, usually written

above it. The limits are always ﬁxed, but the dummy index can be any

symbol one wishes to use except the symbols used in the expression being

summed. Therefore, all the following sums are identical:



i=1



k=1



α=1



♣=1

♣



ℵ=1

ℵ

. (9.4)

It is not a good idea, however, to use a or x as the dummy index for the

summation above!

When adding or subtracting sums of equal length, it is better to use the

same symbol for the dummy index of the sum:



i=1



♥=1

♥



i=1

+ b



♥=1

♥

+ b

♥



k=1

+ b

However,

Box 9.2.1. When multiplying two sums (not necessarily of equal length),

it is essential to choose two diﬀerent dummy indices for the two sums.

9.2 Summations 263

Thus, to multiply



i=1



i=1

,onewrites



i=1



j=1



i=1



j=1

Failure to obey this simple rule can lead to catastrophe. For example, one

may end up with



i=1



i=1



i=1



i=1

, which is a sum of terms

of the form a

+ a

+ ···, excluding terms such as a

or a

,etc.

The freedom of choice for the symbol of dummy index can be used to ma-

nipulate sums and get results very quickly. As an example, suppose that {a

}

is a set of (doubly indexed) numbers which are symmetric under interchange

of their indices, i.e., a

= a

. Similarly, suppose that b

are antisymmet-

ric under interchange of their indices, i.e., b

= −b

. Furthermore, assume

that i and j have the lower limit of 1 and the upper limit of n.Whatis



i=1



j=1

? Call this sum S. Since the choice of the dummy symbol

is irrelevant, we have

S =



i=1



j=1



α=1



β=1

αβ

= −



α=1



β=1

βα

, (9.5)

where we used the symmetry of a

and the antisymmetry of b

.Sincethe

order of summation is irrelevant, we can write S as S = −



β=1



α=1

βα

Once again, change the dummy symbols: Choose i for β and j for α.Then

Equation (9.5) becomes

S = −



i=1



j=1

= −S ⇒ 2S =0 ⇒ S =0.

As another illustration, suppose we want to multiply



i=0

and



i=0

and express the coeﬃcient of a typical power of t in the product in terms of

and b

. Call the product P .Then

P =



i=0



j=0



i=0



j=0

i+j

We need to use a single symbol for the power of t in the double sum. So, let

α = i + j. Our goal is to write P =



, ﬁnd c

in terms of a

and b

and determine the lower and upper limits of the summation on α. The latter

is easy: α has a lower limit of 0 (when both i and j are zero), and an upper

limit of M + N.

For the second dummy index we choose one of the original indices, say i.

The limits of i cannot be the original limits, because i is now mixed up with

α and j through j = α −i. Because of the original bounds of i and j,wehave

0 ≤ i ≤ M as well as

0 ≤ α − i ≤ N or − α ≤−i ≤ N − α or α ≥ i ≥ α − N.

264 Inﬁnite Series

Since i is greater than both 0 and α−N, it must be greater than the maximum

of the two: i ≥ max(0,α− N). This means that the lower limit of the i-

summation is max(0,α− N). Similarly, since i is smaller than both M and

α, it must be smaller than the minimum of the two: i ≤ min(M, α), making

the upper limit of the i-summation min(M,α). We therefore have

P =

M+N



α=0

min(M,α)



i=max(0,α−N)

α−i

M+N



α=0

⎛

⎝

min(M,α)



i=max(0,α−N)

α−i

⎞

⎠



 

≡c

. (9.6)

Example 9.2.1.

As further practice in working with the summation symbol, we

show that the torque on a collection of particles is caused by external forces only.

The torques due to the internal forces add up to zero. We have already illustrated

this for three particles in Example 1.3.5. Here, we generalize the result to any

number of particles.

We use the second formula in Equation (1.31) and separate the forces

T =



k=1

× F



k=1

⎛

⎝

(ext)



i=k

⎞

⎠

(ext)

  



k=1

× F

(ext)

(int)

  



k=1



i=k

× F

We need to show that the double sum is zero. To do so, we break the inner sum

into two parts, i>kand i<k. This yields

(int)

≡



i,k=1

i=k

× F



i,k=1

i>k

× F



i,k=1

i<k

× F



i,k=1

i>k

× F

−



i,k=1

i<k

× F

because, by the third law of motion, F

= −F

. Now, in the second sum, change

the dummy indices twice:

(int)



i,k=1

i>k

× F

−



α,β=1

α>β

× F

βα



i,k=1

i>k

× F

−



i,k=1

i>k

× F



i,k=1

i>k

− r

) × F

As in Example 1.3.5, we assume that F

and r

−r

lie along the same line in which

case the cross products in the sum are all zero.



9.2 Summations 265

In the sequel, we shall have many occasions to use summations and ma-

nipulate them in ways similar to above. The reader is urged to go through

such manipulations with great care and diligence. The skill of summation

techniques is acquired only through such diligent pursuit.

9.2.1 Mathematical Induction

Many a time it is desirable to make a mathematical statement that is true

for all natural numbers. For example, we may want to establish a formula

involving an integer parameter that will hold for all positive integers. One

encounters this situation when, after experimenting with the ﬁrst few positive

integers, one recognizes a pattern and discovers a formula, and wants to make

sure that the formula holds for all natural numbers. For this purpose, one

uses mathematical induction. The essence of mathematical induction is

stated in

induction principle

Box 9.2.2. (Mathematical Induction). Suppose that there is asso-

ciated with a natural number (positive integer) n a statement S

.Then

is true for every positive integer provided the following two conditions

hold:

1. S

is true.

2. If S

is true for some given positive integer m,thenS

m+1

is also

true.

We illustrate the use of mathematical induction by proving the binomial

theorem:

binomial theorem

(a + b)



k=0





m−k



k=0

k!(m −k)!

m−k

= a

+ ma

m−1

b +

m(m −1)

m−2

+ ···+ mab

m−1

+ b

, (9.7)

where we have used the shorthand notation





≡

k!(m − k)!

. (9.8)

The mathematical statement S

is Equation (9.7). We note that S

is trivially

true: (a + b)

= a + b. Now we assume that S

is true and show that S

m+1

is also true. This means starting with Equation (9.7) and showing that

(a + b)

m+1



k=0



m +1



m+1−k